21.3: Construcciones Geométricas

Última actualización
Guardar como PDF

Page ID: 111078

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En la antigua Grecia, se planteaban tres problemas clásicos. Estos problemas son de naturaleza geométrica e involucran construcciones rectas y brújula a partir de lo que ahora es geometría de secundaria; es decir, se nos permite usar solo una recta y brújula para resolverlos. Los problemas se pueden exponer de la siguiente manera.

Dado un ángulo arbitrario, ¿se puede trisecar el ángulo en tres subángulos iguales usando solo una recta y una brújula?
Dado un círculo arbitrario, ¿se puede construir un cuadrado con la misma área usando solo una recta y una brújula?
Dado un cubo, ¿se puede construir el borde de otro cubo que tenga el doble de volumen que el original? Nuevamente, solo se nos permite usar una recta y brújula para hacer la construcción.

Después de desconcertar a los matemáticos durante más de dos mil años, cada una de estas construcciones finalmente se demostró que era imposible. Utilizaremos la teoría de los campos para aportar una prueba de que las soluciones no existen. Es bastante notable que la largamente buscada solución a cada uno de estos tres problemas geométricos provino del álgebra abstracta.

Primero, determinemos más específicamente a qué nos referimos con una recta y brújula, y también examinemos la naturaleza de estos problemas con un poco más de profundidad. Para empezar, una recta no es una regla. No podemos medir longitudes arbitrarias con una recta. Se trata simplemente de una herramienta para trazar una línea a través de dos puntos. La afirmación de que la trisección de un ángulo arbitrario es imposible significa que hay al menos un ángulo que es imposible de trisectar con una construcción recta y brújula. Ciertamente es posible trisectar un ángulo en casos especiales. Podemos construir un$30^\circ$ ángulo; por lo tanto, es posible trisectar un$90^\circ$ ángulo. No obstante, demostraremos que es imposible construir un$20^\circ$ ángulo. Por lo tanto, no podemos trisectar un$60^\circ$ ángulo.

Números Constructibles

Un número real$\alpha$ es construible si podemos construir un segmento de línea de longitud$| \alpha |$ en un número finito de pasos a partir de un segmento de unidad de longitud usando una recta y una brújula.

Teorema$21.37$

El conjunto de todos los números reales constructibles forma un subcampo$F$ del campo de números reales.

Prueba: Dejar$\alpha$ y$\beta$ ser números constructibles. Debemos demostrar que$\alpha + \beta\text{,}$$\alpha - \beta\text{,}$$\alpha \beta\text{,}$ y$\alpha / \beta$ ($\beta \neq 0$) también son números edificables. Podemos suponer que ambos$\alpha$ y$\beta$ son positivos con$\alpha \gt \beta\text{.}$ Es bastante obvio cómo construir$\alpha + \beta$ y$\alpha - \beta\text{.}$ Para encontrar un segmento de línea con longitud$\alpha \beta\text{,}$ asumimos que$\beta \gt 1$ y construimos el triángulo en Figura$21.38$ tal que triángulos$\triangle ABC$ y $\triangle ADE$son similares. Ya que$\alpha / 1 = x / \beta\text{,}$ el segmento de línea$x$ tiene longitud Se puede hacer$\alpha \beta\text{.}$ una construcción similar si la$\beta \lt 1\text{.}$ dejaremos como un ejercicio para mostrar que el mismo triángulo se puede usar para construir$\alpha / \beta$ para$\beta \neq 0\text{.}$

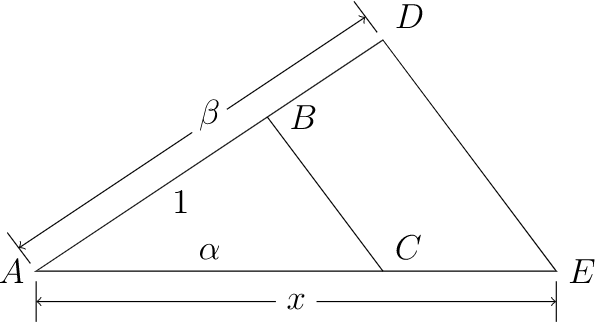
$clipboard_eeed5c17bb29eea88db6fa03dae25709c.png$

$Figure \text { } 21.38.$Construcción de productos

Lema$21.39$

Si$\alpha$ es un número construible, entonces$\sqrt{\alpha}$ es un número edificable.

Prueba: En$21.40$ la Figura los triángulos$\triangle ABD\text{,}$$\triangle BCD\text{,}$ y$\triangle ABC$ son similares; por lo tanto,$1 /x = x / \alpha\text{,}$ o$x^2 = \alpha\text{.}$

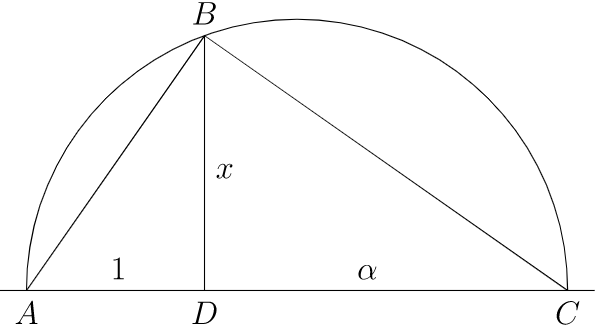
$clipboard_ec73c4c9dbab4977931645adcf26aa5a8.png$

$Figure \text { } 21.40.$Construcción de raíces

Por teorema$21.37$, podemos ubicar en el plano cualquier punto$P =( p, q)$ que tenga coordenadas racionales$p$ y$q\text{.}$ Necesitamos saber qué otros puntos se pueden construir con una brújula y rectitud a partir de puntos con coordenadas racionales.

Lema$21.41$

Dejar$F$ ser un subcampo de${\mathbb R}\text{.}$

Si una línea contiene dos puntos en$F\text{,}$ entonces tiene la ecuación$a x + by + c = 0\text{,}$ donde$a\text{,}$$b\text{,}$ y$c$ están en$F\text{.}$
Si un círculo tiene un centro en un punto con coordenadas en$F$ y un radio que también está en$F\text{,}$ entonces tiene la ecuación$x^2 + y^2 + d x + e y + f = 0\text{,}$ donde$d\text{,}$$e\text{,}$ y$f$ están en$F\text{.}$

Prueba

Dejar$(x_1, y_1)$ y$(x_2, y_2)$ ser puntos en una línea cuyas coordenadas están en$F\text{.}$ Si$x_1 = x_2\text{,}$ entonces la ecuación de la línea a través de los dos puntos es la$x - x_1 = 0\text{,}$ que tiene la forma$a x + by + c = 0\text{.}$ Si$x_1 \neq x_2\text{,}$ entonces la ecuación de la línea a través de los dos puntos viene dada por

\[ y - y_1 = \left( \frac{y_2 - y_1}{x_2 - x_1} \right) (x - x_1)\text{,} \nonumber \]

que también se puede poner en la forma adecuada.

Para probar la segunda parte del lema, supongamos que$(x_1, y_1)$ es el centro de un círculo de radio$r\text{.}$ Entonces el círculo tiene la ecuación

\[ (x - x_1)^2 + (y - y_1)^2 - r^2 = 0\text{.} \nonumber \]

Esta ecuación se puede poner fácilmente en la forma apropiada.

Comenzando con un campo de números constructibles,$F\text{,}$ tenemos tres formas posibles de construir puntos adicionales${\mathbb R}$ con una brújula y una recta.

Para encontrar posibles nuevos puntos en${\mathbb R}\text{,}$ podemos tomar la intersección de dos líneas, cada una de las cuales pasa por dos puntos conocidos con coordenadas en$F\text{.}$
La intersección de una línea que pasa por dos puntos que tienen coordenadas adentro$F$ y un círculo cuyo centro tiene coordenadas adentro$F$ con radio de una longitud$F$ adentro dará nuevos puntos en${\mathbb R}\text{.}$
Podemos obtener nuevos puntos${\mathbb R}$ cruzando dos círculos cuyos centros tienen coordenadas en$F$ y cuyos radios son de longitudes en$F\text{.}$

El primer caso no da nuevos puntos en${\mathbb R}\text{,}$ ya que la solución de dos ecuaciones de la forma$a x + by + c = 0$ que tienen coeficientes en siempre$F$ estará en$F\text{.}$ El tercer caso se puede reducir al segundo caso. Let

\ begin {reunir*} x^2 + y^2 + d_1 x + e_1 y + f_1 = 0\\ x^2 + y^2 + d_2 x + e_2 y + f_2 = 0\ end {reunir*}

ser las ecuaciones de dos círculos, donde$d_i\text{,}$$e_i\text{,}$ y$f_i$ están en$F$ para$i = 1, 2\text{.}$ Estos círculos tienen la misma intersección que el círculo

\[ x^2 + y^2 + d_1 x +e_1 x + f_1 = 0 \nonumber \]

y la línea

\[ (d_1 - d_2) x + b(e_2 - e_1)y + (f_2 - f_1) = 0\text{.} \nonumber \]

La última ecuación es la del acorde que pasa por los puntos de intersección de los dos círculos. De ahí que la intersección de dos círculos se pueda reducir al caso de una intersección de una línea con un círculo.

Considerando el caso de la intersección de una línea y un círculo, debemos determinar la naturaleza de las soluciones de las ecuaciones

\ begin {alinear*} a x + por + c & = 0\\ x^2 + y^2 + d x + e y + f & = 0\ text {.} \ end {alinear*}

Si eliminamos$y$ de estas ecuaciones, obtenemos una ecuación de la forma$Ax^2 + B x + C = 0\text{,}$ donde$A\text{,}$$B\text{,}$ y$C$ están en$F\text{.}$ La$x$ coordenada de los puntos de intersección viene dada por

\[ x = \frac{- B \pm \sqrt{B^2 - 4 A C} }{2 A} \nonumber \]

y es en$F( \sqrt{\alpha}\, )\text{,}$ donde$\alpha = B^2 - 4 A C \gt 0\text{.}$ hemos probado el siguiente lema.

Lema$21.42$

Dejar$F$ ser un campo de números constructibles. Entonces los puntos determinados por las intersecciones de líneas y círculos en se$F$ encuentran en el campo$F( \sqrt{\alpha}\, )$ para algunos$\alpha$ en$F\text{.}$

Teorema$21.43$

Un número real$\alpha$ es un número construible si y solo si existe una secuencia de campos

\[ {\mathbb Q} = F_0 \subset F_1 \subset \cdots \subset F_k \nonumber \]

tal que$F_i = F_{i-1}( \sqrt{ \alpha_i}\, )$ con$\alpha_i \in F_i$ y$\alpha \in F_k\text{.}$ En particular, existe un entero$k \gt 0$ tal que$[{\mathbb Q}(\alpha) : {\mathbb Q} ] = 2^k\text{.}$

Prueba: La existencia de los$F_i$'s y los$\alpha_i$'s es consecuencia directa del Lema 21.42 y del hecho de que

\[ [F_k: {\mathbb Q}] = [F_k : F_{k - 1}][F_{k - 1} : F_{k - 2}] \cdots [F_1: {\mathbb Q} ] = 2^k\text{.} \nonumber \]

Corolario$21.44$

El campo de todos los números constructibles es una extensión algebraica de\ ({\ mathbb Q}\ text { . }\

Como podemos ver por el campo de los números constructibles, no toda extensión algebraica de un campo es una extensión finita.

Duplicar el cubo y cuadrar el círculo

Ahora estamos listos para investigar los problemas clásicos de duplicar el cubo y cuadrar el círculo. Podemos usar el campo de números constructibles para mostrar exactamente cuándo se puede lograr una construcción geométrica particular.

Duplicar el cubo es imposible.

Dado el borde del cubo, es imposible construir con una recta y brújula el borde del cubo que tiene el doble de volumen del cubo original. Que el cubo original tenga un borde de longitud$1$ y, por lo tanto, un volumen de$1\text{.}$ Si pudiéramos construir un cubo que tenga un volumen de$2\text{,}$ entonces este nuevo cubo tendría un borde de longitud$\sqrt[3]{2}\text{.}$ Sin embargo,$\sqrt[3]{2}$ es un cero del polinomio irreducible$x^3 -2$ sobre de${\mathbb Q}\text{;}$ ahí,

\[ [{\mathbb Q}(\sqrt[3]{2}\, ) : {\mathbb Q}] = 3 \nonumber \]

Esto es imposible, ya que no$3$ es un poder de$2\text{.}$

Cuadrando el círculo.

Supongamos que tenemos un círculo de radio$1\text{.}$ El área del círculo es$\pi\text{;}$ por lo tanto, debemos ser capaces de construir un cuadrado con lado$\sqrt{\pi}\text{.}$ Esto es imposible ya que$\pi$ y consecuentemente$\sqrt{\pi}$ son ambos trascendentales. Por lo tanto, usando una recta y brújula, no es posible construir un cuadrado con la misma área que el círculo.

Trisecar un ángulo

Trisectar un ángulo arbitrario es imposible. Demostraremos que es imposible construir un$20^\circ$ ángulo. En consecuencia, no se puede trisectar un$60^{\circ}$ ángulo. Primero necesitamos calcular la fórmula de triple ángulo para el coseno:

\ begin {align*}\ cos 3\ theta & =\ cos (2\ theta +\ theta)\\ & =\ cos 2\ theta\ cos\ theta -\ sin 2\ theta\ sin\ theta\ & = (2\ cos^2\ theta - 1)\ cos\ theta - 2\ sin^2\ theta\ cos\ theta\ cos\ theta\ & = (2\ cos^2\ theta - 1)\ cos\ theta - 2 (1-\ cos^2\ theta)\ cos\ theta\\ & = 4\ cos^3\ theta - 3\ cos\ theta\ texto {.} \ end {alinear*}

El ángulo se$\theta$ puede construir si y solo si$\alpha = \cos \theta$ es construible. Let$\theta = 20^{\circ}\text{.}$ Then$\cos 3 \theta = \cos 60^\circ = 1/2\text{.}$ Por la fórmula de triple ángulo para el coseno,

\[ 4 \alpha^3 - 3 \alpha = \frac{1}{2}\text{.} \nonumber \]

Por lo tanto,$\alpha$ es un cero de$8 x^3 - 6 x -1\text{.}$ Este polinomio no tiene factores en${\mathbb Z}[x]\text{,}$ y por lo tanto es irreducible sobre${\mathbb Q}[x]\text{.}$ Así,$[{\mathbb Q}( \alpha ) : {\mathbb Q }] = 3\text{.}$ Consecuentemente,$\alpha$ no puede ser un número construible.

Nota Histórica

La teoría algebraica de números utiliza las herramientas del álgebra para resolver problemas en la teoría de números. La teoría algebraica moderna de números comenzó con Pierre de Fermat (1601—1665). Ciertamente podemos encontrar muchos enteros positivos que satisfacen la ecuación$x^2 + y^2 = z^2\text{;}$ Fermat conjeturó que la ecuación no$x^n + y^n = z^n$ tiene soluciones enteras positivas para$n \geq 3\text{.}$ Declaró en el margen de su copia de la traducción latina de Aritmética de Diofantus que había encontrado una maravillosa prueba de este teorema, pero que el margen del libro era demasiado estrecho para contenerlo. Sobre la base del trabajo de otros matemáticos, fue Andrew Wiles quien finalmente logró probar el último teorema de Fermat en la década de 1990. El logro de Wiles fue reportado en la portada del New York Times.

Los intentos de probar el último teorema de Fermat han llevado a importantes contribuciones a la teoría algebraica de números por matemáticos tan notables como Leonhard Euler (1707—1783). Los avances significativos en la comprensión del último teorema de Fermat fueron realizados por Ernst Kummer (1810—1893). El estudiante de Kummer, Leopold Kronecker (1823—1891), se convirtió en uno de los principales algebraistas del siglo XIX. La teoría de los ideales de Kronecker y su estudio de la teoría algebraica numérica agregaron mucho a la comprensión de los campos.

David Hilbert (1862-1943) y Hermann Minkowski (1864-1909) estuvieron entre los matemáticos que lideraron el camino en este tema a principios del siglo XX. Hilbert y Minkowski fueron matemáticos en la Universidad de Göttingen en Alemania. Gotinga fue verdaderamente uno de los centros más importantes de investigación matemática durante los últimos dos siglos. El gran número de matemáticos excepcionales que allí estudiaron incluyeron a Gauss, Dirichlet, Riemann, Dedekind, Noether y Weyl.

André Weil respondió preguntas en teoría de números utilizando geometría algebraica, un campo de las matemáticas que estudia la geometría mediante el estudio de anillos conmutativos. De aproximadamente 1955 a 1970, Alexander Grothendieck dominó el campo de la geometría algebraica. Pierre Delgne, estudiante de Grothendieck, resolvió varias de las conjeturas teóricas numéricas de Weil. Una de las contribuciones más recientes al álgebra y la teoría de números es la prueba de Gerd Falting de la conjetura de Mordell-Weil. Esta conjetura de Mordell y Weil dice esencialmente que ciertos polinomios$p(x, y)$ en${\mathbb Z}[x,y]$ tienen sólo un número finito de soluciones integrales.