21.2: Dividir campos

Dejar\(F\) ser un campo y\(p(x)\) ser un polinomio no constante en Ya\(F[x]\text{.}\) sabemos que podemos encontrar una extensión de campo de\(F\) que contenga una raíz de\(p(x)\text{.}\) Sin embargo, nos gustaría saber si una extensión\(E\) de\(F\) contener todas las raíces de\(p(x)\) existe. En otras palabras, ¿podemos encontrar una extensión de campo de\(F\) tal manera que\(p(x)\) los factores en un producto de polinomios lineales? ¿Cuál es la extensión “más pequeña” que contiene todas las raíces de\(p(x)\text{?}\)

Dejar\(F\) ser un campo y\(p(x) = a_0 + a_1 x + \cdots + a_n x^n\) ser un polinomio no constante en\(F[x]\text{.}\) Un campo\(E\) de extensión de\(F\) es un campo de división de\(p(x)\) si existen elementos\(\alpha_1, \ldots, \alpha_n\) en\(E\) tal que\(E = F( \alpha_1, \ldots, \alpha_n )\) y

\[ p(x) = ( x - \alpha_1 )(x - \alpha_2) \cdots (x - \alpha_n)\text{.} \nonumber \]

Un polinomio\(p(x) \in F[x]\) se divide\(E\) si es el producto de factores lineales en\(E[x]\text{.}\)

Ejemplo\(21.29\).

Let\(p(x) = x^4 + 2x^2 - 8\) be in\({\mathbb Q}[x]\text{.}\) Entonces

Solución

\(p(x)\)tiene factores irreducibles\(x^2 -2\) y\(x^2 + 4\text{.}\) Por lo tanto, el campo\({\mathbb Q}( \sqrt{2}, i )\) es un campo de división para\(p(x)\text{.}\)

Ejemplo\(21.30\).

Let\(p(x) = x^3 - 3\) be in\({\mathbb Q}[x]\text{.}\) Entonces\(p(x)\) tiene una raíz en el campo\({\mathbb Q}( \sqrt[3]{3}\, )\text{.}\)

Solución

Sin embargo, este campo no es un campo de división\(p(x)\) ya que las complejas raíces cubicas de 3,

\[ \frac{ -\sqrt[3]{3} \pm (\sqrt[6]{3}\, )^5 i }{2}\text{,} \nonumber \]

no están en\({\mathbb Q}( \sqrt[3]{3}\, )\text{.}\)

Teorema\(21.31\).

Dejar\(p(x) \in F[x]\) ser un polinomio no constante. Entonces existe un campo de división\(E\) para\(p(x)\text{.}\)

Prueba

Vamos a utilizar la inducción matemática en el grado de\(p(x)\text{.}\) Si\(\deg p(x) = 1\text{,}\) entonces\(p(x)\) es un polinomio lineal y\(E = F\text{.}\) Supongamos que el teorema es cierto para todos los polinomios de grado\(k\) con\(1 \leq k \lt n\) y dejar\(\deg p(x) = n\text{.}\) Podemos suponer que\(p(x)\) es irreducible; de lo contrario, por nuestro hipótesis de inducción, hemos terminado. Por teorema\(21.5\), existe un campo\(K\) tal que\(p(x)\) tiene un cero\(\alpha_1\) en\(K\text{.}\) Por lo tanto,\(p(x) = (x - \alpha_1)q(x)\text{,}\) donde\(q(x) \in K[x]\text{.}\) Ya que\(\deg q(x) = n -1\text{,}\) existe un campo\(E \supset K\) de división de\(q(x)\) que contiene los ceros\(\alpha_2, \ldots, \alpha_n\) de\(p(x)\) por nuestra inducción hipótesis. En consecuencia,

\[ E = K(\alpha_2, \ldots, \alpha_n) = F(\alpha_1, \ldots, \alpha_n) \nonumber \]

es un campo de división de\(p(x)\text{.}\)

La cuestión de la singularidad surge ahora para dividir campos. A esta pregunta se le responde afirmativamente. Dados dos campos\(L\) de división\(K\) y de un polinomio\(p(x) \in F[x]\text{,}\) existe un isomorfismo de campo\(\phi : K \rightarrow L\) que preserva\(F\text{.}\) Para probar este resultado, primero debemos probar un lema.

Teorema\(21.32\).

\(\phi : E \rightarrow F\)Déjese ser un isomorfismo de campos. Dejar\(K\) ser un campo de extensión de\(E\) y\(\alpha \in K\) ser algebraico sobre\(E\) con polinomio mínimo\(p(x)\text{.}\) Supongamos que\(L\) es un campo de extensión de\(F\) tal que\(\beta\) es raíz del polinomio en\(F[x]\) obtenido de\(p(x)\) debajo de la imagen de \(\phi\text{.}\)Luego\(\phi\) se extiende a un isomorfismo único\(\overline{\phi} : E( \alpha ) \rightarrow F( \beta )\) tal que\(\overline{\phi}( \alpha ) = \beta\) y\(\overline{\phi}\) concuerda con\(\phi\)\(E\text{.}\)

Prueba

Si\(p(x)\) tiene grado\(n\text{,}\) entonces por Teorema\(21.13\) podemos escribir cualquier elemento en\(E( \alpha )\) como una combinación lineal de\(1, \alpha, \ldots, \alpha^{n - 1}\text{.}\) Por lo tanto, el isomorfismo que estamos buscando debe ser

\[ \overline{\phi}( a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1}) = \phi(a_0) + \phi(a_1) \beta + \cdots + \phi(a_{n - 1}) \beta^{n - 1}\text{,} \nonumber \]

donde

\[ a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1} \nonumber \]

es un elemento en\(E(\alpha)\text{.}\) El hecho de que\(\overline{\phi}\) sea un isomorfismo podría comprobarse por cómputo directo; sin embargo, es más fácil observar que\(\overline{\phi}\) es una composición de mapas que ya sabemos que son isomorfismos.

Podemos extender\(\phi\) para ser un isomorfismo del\(E[x]\)\(F[x]\text{,}\) que también denotaremos\(\phi\text{,}\) dejando

\[ \phi( a_0 + a_1 x + \cdots + a_n x^n ) = \phi( a_0 ) + \phi(a_1) x + \cdots + \phi(a_n) x^n\text{.} \nonumber \]

Esta extensión concuerda con el isomorfismo original\(\phi : E \rightarrow F\text{,}\) ya que los polinomios constantes se mapean a polinomios constantes. Por suposición, de\(\phi(p(x)) = q(x)\text{;}\) ahí\(\langle p(x) \rangle\),\(\phi\) mapas en\(\langle q(x) \rangle\text{.}\) Consecuentemente, tenemos un isomorfismo\(\psi : E[x] / \langle p(x) \rangle \rightarrow F[x]/\langle q(x) \rangle\text{.}\) Por Proposición\(21.12\), tenemos isomorfismos\(\sigma: E[x]/\langle p(x) \rangle \rightarrow E(\alpha)\) y\(\tau : F[x]/\langle q(x) \rangle \rightarrow F( \beta )\text{,}\) definidos por evaluación en\(\alpha\) y\(\beta\text{,}\) respectivamente. Por lo tanto,\(\overline{\phi} = \tau \psi \sigma^{-1}\) es el isomorfismo requerido (ver Figura\(21.33\)).

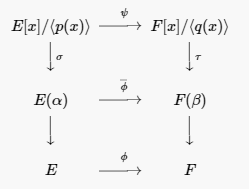
\(Figure \text { } 21.33.\)

Dejamos la prueba de singularidad como ejercicio.

 

Teorema\(21.34\).

Dejar\(\phi : E \rightarrow F\) ser un isomorfismo de campos y dejar\(p(x)\) ser un polinomio no constante en\(E[x]\) y\(q(x)\) el polinomio correspondiente en\(F[x]\) debajo del isomorfismo. Si\(K\) es un campo de división de\(p(x)\) y\(L\) es un campo de división de\(q(x)\text{,}\) entonces\(\phi\) se extiende a un isomorfismo\(\psi : K \rightarrow L\text{.}\)

Prueba

Vamos a utilizar la inducción matemática en el grado de\(p(x)\text{.}\) Podemos suponer que\(p(x)\) es irreducible sobre\(E\text{.}\) Por lo tanto, también\(q(x)\) es irreducible sobre\(F\text{.}\) Si\(\deg p(x) = 1\text{,}\) entonces por la definición de un campo de división,\(K = E\)\(L = F\) y no hay nada que probar.

Supongamos que el teorema sostiene para todos los polinomios de grado menor que\(n\text{.}\) Dado que\(K\) es un campo de división de\(p(x)\text{,}\) todas las raíces de\(p(x)\) están en\(K\text{.}\) Elige una de estas raíces, digamos\(\alpha\text{,}\) tal que\(E \subset E( \alpha ) \subset K\text{.}\) De igual manera, podemos encontrar una raíz\(\beta\) de\(q(x)\) en \(L\)tal que\(F \subset F( \beta) \subset L\text{.}\) Por Lemma\(21.32\), existe un isomorfismo\(\overline{\phi} : E(\alpha ) \rightarrow F( \beta)\) tal que\(\overline{\phi}( \alpha ) = \beta\) y\(\overline{\phi}\) concuerda con\(\phi\) on\(E\) (ver Figura\(21.35\)).

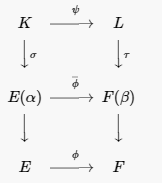
\(Figure \text { } 21.35.\)

Ahora escribe\(p(x) = (x - \alpha ) f(x)\) y\(q(x) = ( x - \beta) g(x)\text{,}\) donde los grados de\(f(x)\) y\(g(x)\) son menores que los grados de\(p(x)\) y\(q(x)\text{,}\) respectivamente. La extensión de campo\(K\) es un campo de división para\(f(x)\) más\(E( \alpha)\text{,}\) y\(L\) es un campo de división para\(g(x)\) más\(F( \beta )\text{.}\) Por nuestra hipótesis de inducción existe un isomorfismo\(\psi : K \rightarrow L\) tal que\(\psi\) concuerda con\(\overline{\phi}\) en\(E( \alpha)\text{.}\) Por lo tanto, existe un isomorfismo\(\psi : K \rightarrow L\) tal que\(\psi\) concuerda con\(\phi\)\(E\text{.}\)

 

Corolario\(21.36\).

\(p(x)\)Sea un polinomio en\(F[x]\text{.}\) Entonces existe un campo\(K\) de división de\(p(x)\) que es único hasta el isomorfismo.