7.1: Homomorfismos
- Page ID
- 117820
Dejar\(G_1\) y\(G_2\) ser grupos. Recordemos que\(\phi:G_1\to G_2\) es un isomorfismo si y solo si\(\phi\)
- es uno a uno,
- está en, y
- satisface la propiedad homomórfica.
Decimos que\(G_1\) es isomórfico\(G_2\) y escribimos\(G_1\cong G_2\) si tal\(\phi\) existe. Hablando vagamente, dos grupos son isomórficos si tienen la “misma estructura”. ¿Qué pasa si dejamos caer el requisito uno a uno y en el requisito?
Dejar\((G_1,*)\) y\((G_2,\odot)\) ser grupos. Una función\(\phi:G_1\to G_2\) es un homomorfismo si y sólo si\(\phi\) satisface la propiedad homomórfica:\[\phi(x*y)=\phi(x)\odot\phi(y)\] para todos\(x,y\in G_1\). A riesgo de introducir ambigüedad, generalmente omitiremos hacer referencia explícita a las operaciones binarias y escribir la propiedad homomórfica como\[\phi(xy)=\phi(x)\phi(y).\]
Los homomorfismos grupales son análogos a las transformaciones lineales en espacios vectoriales que se encuentran en álgebra lineal.
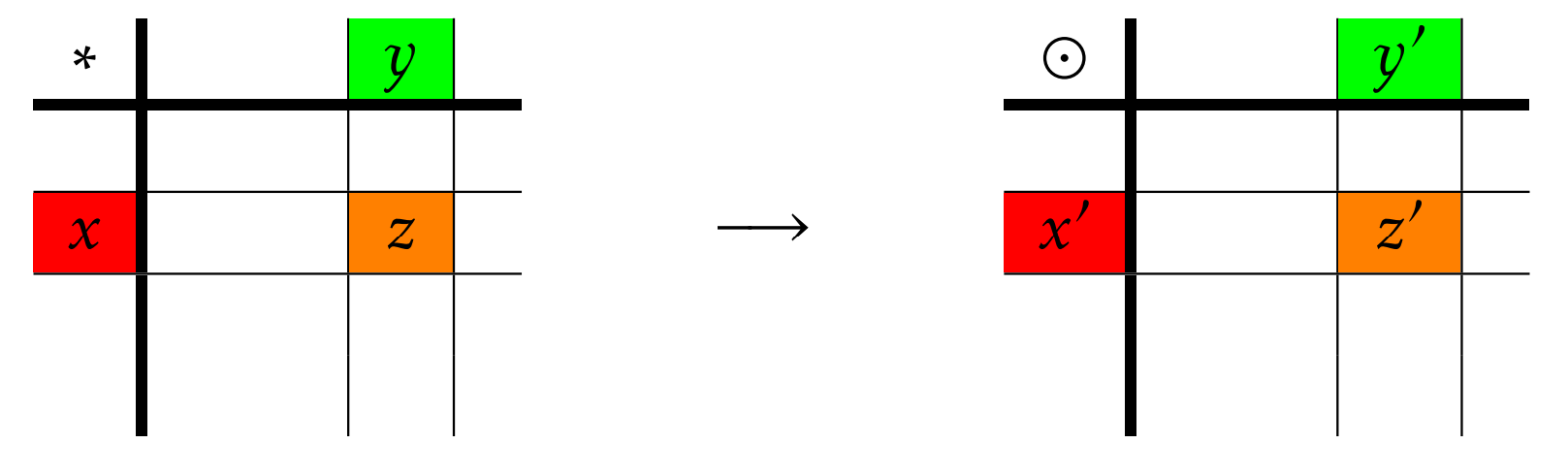
La figura\(\PageIndex{1}\) captura una representación visual de la propiedad homomórfica. Encontramos esta misma representación en la Figura\(\PageIndex{1}\). Si\(\phi(x)=x'\),\(\phi(y)=y'\), y\(\phi(z)=z'\) mientras\(z'=x'\odot y'\), entonces la única manera\(G_2\) de respetar la estructura de\(G_1\) es para\[\phi(x*y)=\phi(z)=z'=x'\odot y'=\phi(x)\odot \phi(y).\]
Definir\(\phi:\mathbb{Z}_3\to D_3\) vía\(\phi(k)=r^k\). Demostrar que\(\phi\) es un homomorfismo y luego determinar si\(\phi\) es uno a uno o sobre. También, tratar de dibujar una imagen del homomorfismo en términos de diagramas de Cayley.
Dejar\(G\) y\(H\) ser grupos. Demostrar que la función\(\phi:G\times H\to G\) dada por\(\phi(g,h)=g\) es un homomorfismo. Esta función es un ejemplo de un mapa de proyección.
Siempre hay al menos un homomorfismo entre dos grupos.
Dejar\(G_1\) y\(G_2\) ser grupos. Definir\(\phi:G_1\to G_2\) vía\(\phi(g)=e_2\) (dónde\(e_2\) está la identidad de\(G_2\)). Entonces\(\phi\) es un homomorfismo. Esta función a menudo se conoce como el homomorfismo trivial o el\(0\) -mapa.
De vuelta en la Sección 3.3, encontramos varios teoremas sobre isomorfismos. Sin embargo, al final de esa sección remarcamos que algunos de esos teoremas no requerían que la función fuera uno a uno y sobre. Recopilamos esos resultados aquí para mayor comodidad.
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo.
- Si\(e_1\) y\(e_2\) son los elementos de identidad de\(G_1\) y\(G_2\), respectivamente, entonces\(\phi(e_1)=e_2\).
- Para todos\(g\in G_1\), tenemos\(\phi(g^{-1})=[\phi(g)]^{-1}\).
- Si\(H\leq G_1\), entonces\(\phi(H)\leq G_2\), donde\[\phi(H):=\{y\in G_2\mid \text{there exists } h\in H\text{ such that }\phi(h)=y\}.\] Note que\(\phi(H)\) se llama la imagen de\(H\). Un caso especial es cuando\(H=G_1\). Observe que\(\phi\) es exactamente cuándo\(\phi(G_1)=G_2\).
El siguiente teorema es una consecuencia del teorema de Lagrange.
Dejar\(G_1\) y\(G_2\) ser grupos tales que\(G_2\) sea finito y dejar\(H\leq G_1\). Si\(\phi:G_1\to G_2\) es un homomorfismo, entonces se\(|\phi(H)|\) divide\(|G_2|\).
El siguiente teorema nos dice que bajo un homomorfismo, el orden de la imagen de un elemento debe dividir el orden de la pre-imagen de ese elemento.
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. Si\(g\in G_1\) tal eso\(|g|\) es finito, entonces se\(|\phi(g)|\) divide\(|g|\).
Cada homomorfismo tiene un subconjunto importante del dominio asociado a él.
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. El kernel de\(\phi\) se define a través de\[\ker(\phi):=\{g\in G_1\mid \phi(g)=e_2\}.\]
El núcleo de un homomorfismo es análogo al espacio nulo de una transformación lineal de espacios vectoriales.
Identificar el núcleo y la imagen para el homomorfismo dado en Problema\(\PageIndex{1}\).
Cuál es el núcleo de un homomorfismo trivial (ver Teorema\(\PageIndex{1}\)).
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. Entonces\(\ker(\phi)\trianglelefteq G_1\).
Seamos\(G\) un grupo y dejemos\(H\trianglelefteq G\). Entonces el mapa\(\gamma:G\to G/H\) dado por\(\gamma(g)=gH\) es un homomorfismo con\(\ker(\gamma)=H\). Este mapa se llama el mapa de proyección canónica.
El resultado de los teoremas\(\PageIndex{5}\) y\(\PageIndex{6}\) es que los granos de homomorfismos son siempre normales y cada subgrupo normal es el núcleo de algún homomorfismo. Resulta que el kernel puede decirnos si\(\phi\) es uno a uno.
El siguiente teorema nos dice que dos elementos en el dominio de un homomorfismo grupal se mapean al mismo elemento en el codominio si y solo si están en el mismo coconjunto del kernel.
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. Entonces\(\phi(a) = \phi(b)\) si y sólo si\(a\in b\ker(\phi)\).
Una consecuencia del Teorema\(\PageIndex{7}\) es que si el núcleo de un homomorfismo tiene orden\(k\), entonces el homomorfismo es\(k\) a-1. Es decir, cada elemento del rango tiene exactamente\(k\) elementos del dominio que le mapean. En particular, cada una de estas colecciones de\(k\) elementos corresponde a un coconjunto del kernel.
Supongamos que\(\phi:\mathbb{Z}_{20}\to\mathbb{Z}_{20}\) es un homomorfismo grupal tal que\(\ker(\phi)=\{0,5,10,15\}\). Si\(\phi(13)=8\), determinar todos los elementos que\(\phi\) mapean a 8.
El siguiente resultado es un caso especial de Teorema\(\PageIndex{7}\).
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. Entonces\(\phi\) es uno a uno si y solo si\(\ker(\phi)=\{e_1\}\), donde\(e_1\) esta la identidad en\(G_1\).
Dejar\(G_1\) y\(G_2\) ser grupos y supongamos que\(\phi:G_1\to G_2\) es un homomorfismo. Dado un conjunto generador para\(G_1\), el homomorfismo\(\phi\) está determinado de manera única por su acción en el conjunto generador para\(G_1\). En particular, si tienes una palabra para un elemento de grupo escrita en términos de los generadores, simplemente aplica la propiedad homomórfica a la palabra para encontrar la imagen del elemento de grupo correspondiente.
Supongamos que\(\phi: Q_8\to V_{4}\) es un grupo homomorfismo satisfactorio\(\phi(i)=h\) y\(\phi(j)=v\).
- Encontrar\(\phi(1)\),\(\phi(-1)\),\(\phi(k)\),\(\phi(-i)\),\(\phi(-j)\), y\(\phi(-k)\).
- Encuentra\(\ker(\phi)\).
- ¿A qué grupo conocido es\(Q_8/\ker(\phi)\) isomórfico?
Encuentra un homomorfismo no trivial desde\(\mathbb{Z}_{10}\) hasta\(\mathbb{Z}_6\).
Encuentra todos los homomorfismos no triviales desde\(\mathbb{Z}_3\) hasta\(\mathbb{Z}_6\).
Demostrar que el único homomorfismo de\(D_3\) a\(\mathbb{Z}_3\) es el homomorfismo trivial.
Dejar\(F\) ser el conjunto de todas las funciones de\(\mathbb{R}\) a\(\mathbb{R}\) y dejar\(D\) ser el subconjunto de funciones diferenciables en\(\mathbb{R}\). Resulta que\(F\) es un grupo bajo adición de funciones y\(D\) es un subgrupo de\(F\) (no es necesario probarlo). Definir\(\phi:D\to F\) vía\(\phi(f)=f'\) (donde\(f'\) es la derivada de\(f\)). Demostrar que\(\phi\) es un homomorfismo. Es posible que recuerde hechos del cálculo sin probarlos. ¿Es\(\phi\) uno a uno? ¿Onto?


