4.3: Determinantes y Volúmenes

Última actualización
Guardar como PDF

Page ID: 113021

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos

Comprender la relación entre el determinante de una matriz y el volumen de un paralelepípedo.
Aprende a usar determinantes para calcular volúmenes de paralelogramos y triángulos.
Aprende a usar determinantes para calcular el volumen de algunas formas curvilíneas como elipses.
Imágenes: paralelepípedo, la imagen de una forma curvilínea bajo una transformación lineal.
Teorema: determinantes y volúmenes.
Vocabulario palabra: paralelepípedo.

En esta sección damos una interpretación geométrica de los determinantes, en términos de volúmenes. Esto arrojará luz sobre la razón detrás de tres de las cuatro propiedades definitorias del determinante, Definición 4.1.1 en la Sección 4.1. También es un ingrediente crucial en la fórmula de cambio de variables en el cálculo multivariable.

Paralelogramos y Paralelepípedos

El determinante calcula el volumen del siguiente tipo de objeto geométrico.

Definición$\PageIndex{1}$: Paralellepiped

El paralelepípedo determinado por los$n$ vectores$v_1, v_2,\ldots,v_n$ en$\mathbb{R}^n $ es el subconjunto

\[ P = \bigl\{a_1x_1 + a_2x_2 + \cdots + a_nx_n \bigm| 0 \leq a_1,a_2,\ldots,a_n\leq 1\bigr\}. \nonumber \]

En otras palabras, un paralelepípedo es el conjunto de todas las combinaciones lineales de$n$ vectores con coeficientes en$[0,1]$. Podemos dibujar paralelepípedos usando la ley de paralelogramo para la adición de vectores.

Ejemplo$\PageIndex{1}$: The Unit Cubte

El paralelepípedo determinado por los vectores de coordenadas estándar$e_1,e_2,\ldots,e_n$ es el cubo$n$ unidimensional.

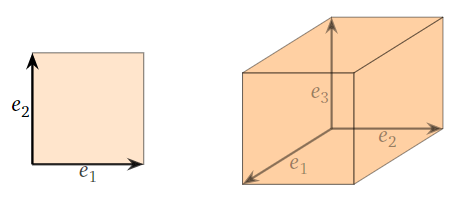
$clipboard_e85e037106e647557d69a7eef7f807287.png$

Figura$\PageIndex{1}$

Ejemplo$\PageIndex{2}$: Parallelograms

Cuando$n = 2\text{,}$ un paralelepípedo es solo un paralelograma en$\mathbb{R}^2 $. Tenga en cuenta que los bordes vienen en pares paralelos.

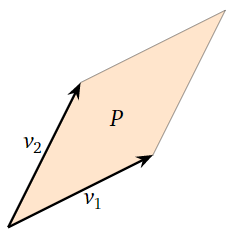
$clipboard_e795c3e4b79086124d7f8ece02f1ea5da.png$

Figura$\PageIndex{2}$

Ejemplo$\PageIndex{3}$

Cuando$n=3\text{,}$ un paralelepípedo es una especie de cubo sesgado. Tenga en cuenta que las caras vienen en pares paralelos.

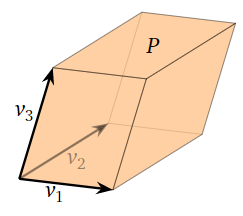
$clipboard_edcf74074ff27cd13d9f62da5ee1826b8.png$

Figura$\PageIndex{3}$

¿Cuándo un paralelepípedo tiene cero volumen? Esto sólo puede suceder si el paralelepípedo es plano, es decir, se aplaste en una dimensión inferior.

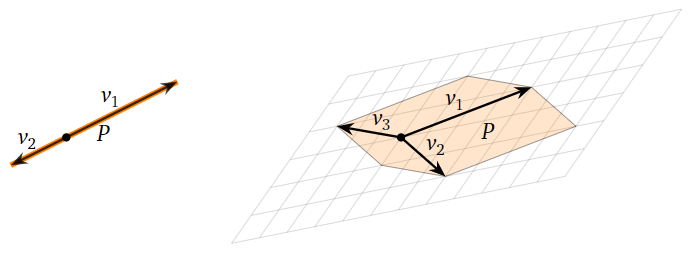
$clipboard_e3ae0654c311649ec99d986554e966479.png$

Figura$\PageIndex{4}$

Esto significa exactamente que$\{v_1,v_2,\ldots,v_n\}$ es linealmente dependiente, lo que por Corolario 4.1.1 en la Sección 4.1 significa que la matriz con filas$v_1,v_2,\ldots,v_n$ tiene un cero determinante. Para resumir:

Observación Clave$\PageIndex{1}$

El paralelepípedo definido por$v_1,v_2,\ldots,v_n$ tiene volumen cero si y sólo si la matriz con filas$v_1,v_2,\ldots,v_n$ tiene determinante cero.

Determinantes y Volúmenes

La observación clave anterior es solo el comienzo de la historia: el volumen de un paralelepípedo es siempre un determinante.

Teorema$\PageIndex{1}$: Determinants and Volumes

Dejar$v_1,v_2,\ldots,v_n$ ser vectores en$\mathbb{R}^n \text{,}$ dejar$P$ ser el paralelepípedo determinado por estos vectores, y dejar$A$ ser la matriz con filas$v_1,v_2,\ldots,v_n$. Entonces el valor absoluto del determinante de$A$ es el volumen de$P\text{:}$

\[ |\det(A)| = \text{vol}(P). \nonumber \]

Prueba

Dado que las cuatro propiedades definitorias, Definición 4.1.1 en la Sección 4.1, caracterizan al determinante, también caracterizan el valor absoluto del determinante. Explícitamente,$|\det|$ es una función sobre matrices cuadradas que satisface estas propiedades:

Hacer un reemplazo de fila en$A$ no cambia$|\det(A)|$.
Escalar una fila de$A$ por un escalar$c$ se multiplica$|\det(A)|$ por$|c|$.
El intercambio de dos filas de una matriz no cambia$|\det(A)|$.
El determinante de la matriz de identidad$I_n$ es igual a$1$.

El valor absoluto del determinante es la única función de este tipo: de hecho, por Receta: Computación de determinantes por reducción de filas en la Sección 4.1, si realiza algún número de operaciones de fila$A$ para obtener una matriz$B$ en forma de escalón de filas, entonces

\[ |\det(A)| = \left|\frac{\text{(product of the diagonal entries of $B$)}} {\text{(product of scaling factors used)}}\right|. \nonumber \]

Para una matriz cuadrada$A\text{,}$ abusamos de la notación y dejamos$\text{vol}(A)$ denotar el volumen del paralelepípedo determinado por las filas de$A$. Entonces podemos considerar$\text{vol}$ como una función desde el conjunto de matrices cuadradas hasta los números reales. Mostraremos que$\text{vol}$ además satisface las cuatro propiedades anteriores.

Por simplicidad, consideramos un reemplazo de fila de la forma$R_n = R_n + cR_i$. El volumen de un paralelepípedo es el volumen de su base, multiplicado por su altura: aquí la “base” es la paralelepípeda determinada por$v_1,v_2,\ldots,v_{n-1}\text{,}$ y la “altura” es la distancia perpendicular$v_n$ de la base.

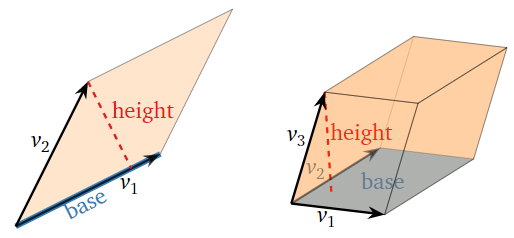
$clipboard_e71160e00c8e7b2eca7e59af5cf639fb4.png$

Figura$\PageIndex{5}$

Trasladando$v_n$ por un múltiplo de$v_i$ movimientos$v_n$ en una dirección paralela a la base. ¡Esto no cambia ni la base ni la altura! Por lo tanto, no$\text{vol}(A)$ se modifica por reemplazos de fila.

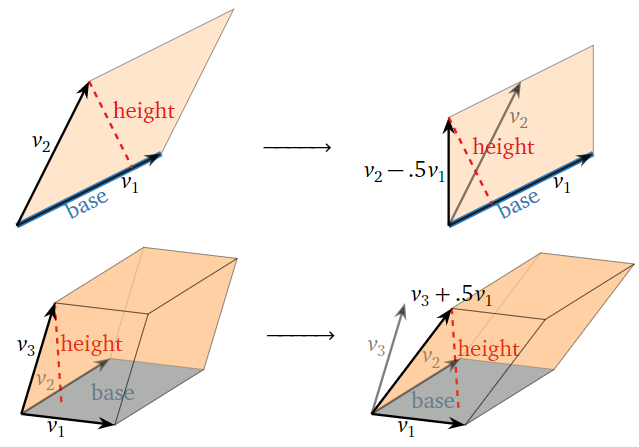
$clipboard_e29842a92b93a439261e05901e156426d.png$

Figura$\PageIndex{6}$

Por simplicidad, consideramos una escala de fila de la forma$R_n = cR_n.$ Esto escala la longitud de$v_n$ por un factor del$|c|\text{,}$ cual también escala la distancia perpendicular de$v_n$ desde la base por un factor de$|c|$. Así,$\text{vol}(A)$ es escalado por$|c|$.

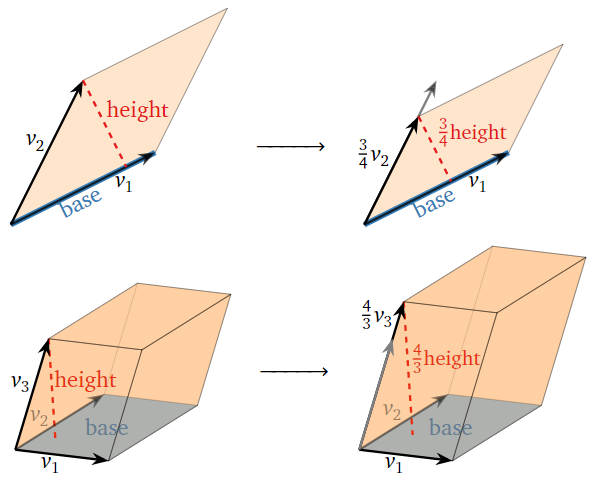
$clipboard_e2baf3c7acf633020b8fc3019ad6fae3a.png$

Figura$\PageIndex{7}$

El intercambio de dos filas de$A$ solo reordena los vectores,$v_1,v_2,\ldots,v_n\text{,}$ por lo tanto, no tiene ningún efecto sobre el paralelepípedo determinado por esos vectores. Por lo tanto, no$\text{vol}(A)$ se modifica por swaps de fila.

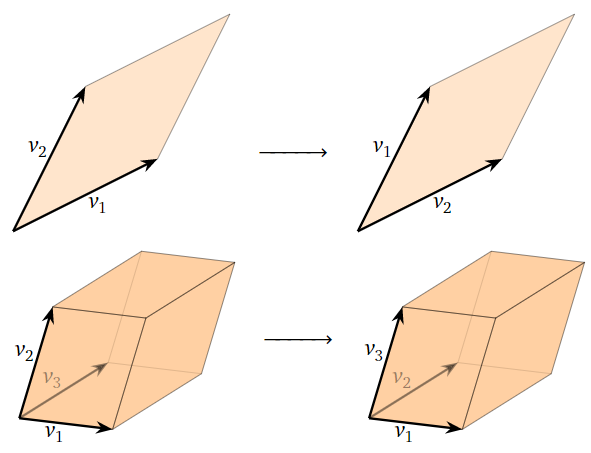
$clipboard_eef6982bf309872c979890292332ce380.png$

Figura$\PageIndex{8}$

Las filas de la matriz de identidad$I_n$ son los vectores de coordenadas estándar$e_1,e_2,\ldots,e_n$. El paralelepípedo asociado es el cubo unitario, que tiene volumen$1$. Así,$\text{vol}(I_n) = 1$.

Dado que$|\det|$ es la única función que satisface estas propiedades, tenemos

\[ \text{vol}(P) = \text{vol}(A) = |\det(A)|. \nonumber \]

Esto completa la prueba.

Ya que$\det(A) = \det(A^T)$ por la propiedad de transposición, Proposición 4.1.4 en la Sección 4.1, el valor absoluto de también$\det(A)$ es igual al volumen del paralelepípedo determinado por las columnas de$A$ también.

Ejemplo$\PageIndex{4}$: Length

Una$1\times 1$ matriz$A$ es sólo un número$\left(\begin{array}{c}a\end{array}\right)$. En este caso, el paralelepípedo$P$ determinado por su una fila es solo el intervalo$[0,a]$ (o$[a,0]$ si$a\lt0$). El “volumen” de una región en$\mathbb{R}^1 = \mathbb{R}$ es apenas su longitud, por lo que es claro en este caso que$\text{vol}(P) = |a|$.

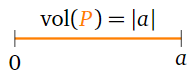
$clipboard_ec6b3c1a1c41e68276a917be470c327ce.png$

Figura$\PageIndex{9}$

Ejemplo$\PageIndex{5}$: Area

Cuando$A$ es una$2\times 2$ matriz, sus filas determinan un paralelogramo en$\mathbb{R}^2 $. El “volumen” de una región en$\mathbb{R}^2 $ es su área, por lo que obtenemos una fórmula para el área de un paralelogramo: es el determinante de la matriz cuyas filas son los vectores que forman dos lados adyacentes del paralelogramo.

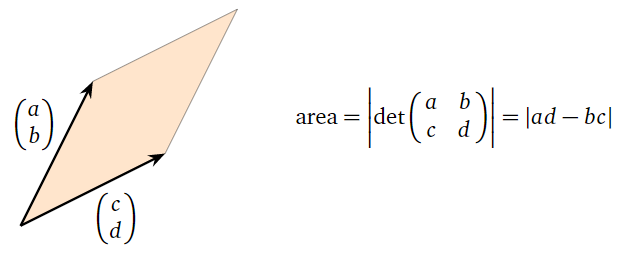
$clipboard_e2817e71743714ff0f02be6d1bc6ed6f3.png$

Figura$\PageIndex{10}$

Quizás sea sorprendente que sea posible calcular el área de un paralelogramo sin trigonometría. Es un divertido problema de geometría probar esta fórmula a mano. [Pista: primero piensa en el caso cuando la primera fila de$A$ yace en el$x$ eje.]

Ejemplo$\PageIndex{6}$

Encuentra el área del paralelogramo con lados$(1,3)$ y$(2,-3)$.

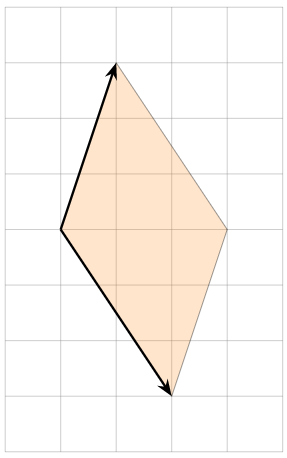
$clipboard_e9e9746c8dab7e8ba5bece83f8cad8ed3.png$

Figura$\PageIndex{11}$

Solución

El área es

\[ \left|\det\left(\begin{array}{cc}1&3\\2&-3\end{array}\right)\right| = |-3-6| = 9. \nonumber \]

Ejemplo$\PageIndex{7}$

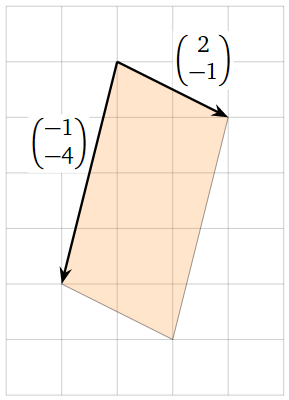
Encuentra el área del paralelogramo en la imagen.

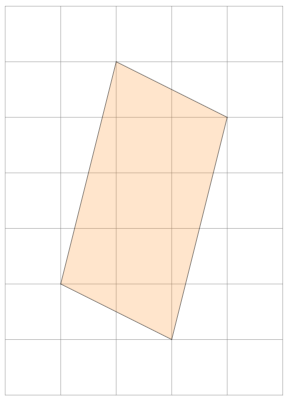
$clipboard_e90f92d08fdd343c40883a789a0b318f5.png$

Figura$\PageIndex{12}$

Solución

Elegimos dos lados adyacentes para ser las filas de una matriz. Elegimos los dos primeros:

$clipboard_ec309659dca41ee107f84132467320202.png$

Figura$\PageIndex{13}$

Tenga en cuenta que no necesitamos saber dónde está el origen en la imagen: los vectores están determinados por su longitud y dirección, no por dónde comienzan. El área es

\[ \left|\det\left(\begin{array}{cc}-1&-4\\2&-1\end{array}\right)\right| = |1+8| = 9. \nonumber \]

Ejemplo$\PageIndex{8}$: Area of a triangle

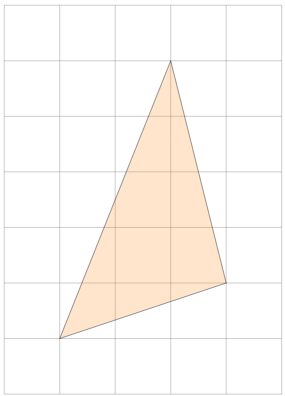
Encuentra el área del triángulo con vértices$(-1,-2), \,(2,-1),\,(1,3).$

$clipboard_eb0dc0b2840b335994f22acb5dfae30ac.png$

Figura$\PageIndex{14}$

Solución

Doblar un triángulo hace un paralelograma. Elegimos dos de sus lados para que sean las filas de una matriz.

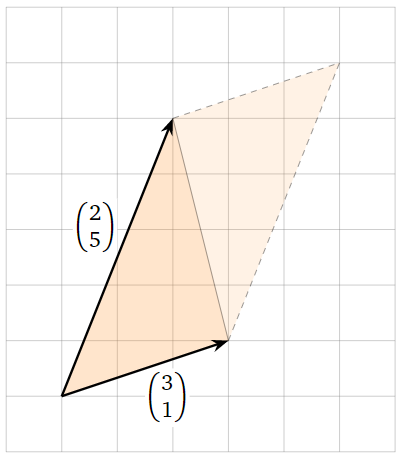
$clipboard_e2d12f4d7748e7b7df3c755e5d55163c5.png$

Figura$\PageIndex{15}$

El área del paralelogramo es

\[ \left|\det\left(\begin{array}{cc}2&5\\3&1\end{array}\right)\right| = |2-15| = 13, \nonumber \]

así que el área del triángulo es$13/2$.

Quizás te preguntes: si el valor absoluto del determinante es un volumen, ¿cuál es el significado geométrico del determinante sin el valor absoluto? El siguiente comentario explica que podemos pensar en el determinante como un volumen firmado. Si has tomado un curso de cálculo integral, probablemente hayas calculado áreas negativas bajo curvas; la idea aquí es similar.

Observación: Volúmenes firmados

El teorema$\PageIndex{1}$ sobre determinantes y volúmenes nos dice que el valor absoluto del determinante es el volumen de un paralelepípedo. Esto plantea la cuestión de si el signo del determinante tiene algún significado geométrico.

Una$1\times 1$ matriz$A$ es sólo un número$\left(\begin{array}{c}a\end{array}\right)$. En este caso, el paralelepípedo$P$ determinado por su una fila es solo el intervalo$[0,a]$ si$a \geq 0\text{,}$ y es$[a,0]$ si$a\lt0$. En este caso, el signo del determinante determina si el intervalo está a la izquierda o a la derecha del origen.

Para una$2\times 2$ matriz con filas$v_1,v_2\text{,}$ el signo del determinante determina si$v_2$ es en sentido antihorario o en sentido horario desde$v_1$. Es decir, si el ángulo en sentido contrario$v_1$ a las agujas del reloj de a$v_2$ es menor que$180^\circ\text{,}$ entonces el determinante es positivo; de lo contrario es negativo (o cero).

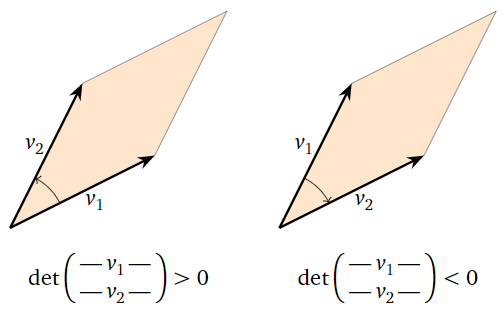
$clipboard_ea295b4d37be522353998e0e3862cb12b.png$

Figura$\PageIndex{16}$

Por ejemplo, si$v_1 = {a\choose b}\text{,}$ entonces la rotación en sentido contrario a las agujas del reloj de$v_1$$v_2 = {-b\choose a}$ by$90^\circ$ es por el Ejemplo 3.3.8 en la Sección 3.3, y

\[ \det\left(\begin{array}{cc}a&b\\-b&a\end{array}\right) = a^2 + b^2 > 0. \nonumber \]

Por otro lado, la rotación en sentido horario de$v_1$ by$90^\circ$ es$b\choose -a\text{,}$ y

\[ \det\left(\begin{array}{cc}a&b\\b&-a\end{array}\right) = -a^2 - b^2 \lt 0. \nonumber \]

Para una$3\times 3$ matriz con filas$v_1,v_2,v_3\text{,}$ la regla de la derecha determina el signo del determinante. Si apunta el dedo índice de su mano derecha en la dirección de$v_1$ y su dedo medio en la dirección de$v_2\text{,}$ entonces el determinante es positivo si su pulgar apunta aproximadamente en la dirección de$v_3\text{,}$ y es negativo de lo contrario.

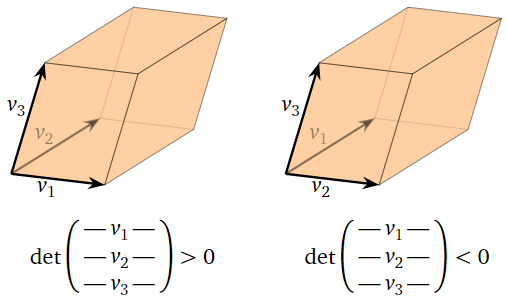
$clipboard_e15c233c79730c48ddde8f9d6dca57b58.png$

Figura$\PageIndex{17}$

En dimensiones superiores, la noción de volumen firmado sigue siendo importante, pero suele definirse en términos del signo de un determinante.

Volúmenes de Regiones

Dejar$A$ ser una$n\times n$ matriz con columnas$v_1,v_2,\ldots,v_n\text{,}$ y dejar$T\colon\mathbb{R}^n \to\mathbb{R}^n $ ser la transformación matricial asociada, Definición 3.1.3 en la Sección 3.1,$T(x)=Ax$. Entonces$T(e_1)=v_1$ y$T(e_2)=v_2\text{,}$ así$T$ lleva el cubo de la unidad$C$ al paralelepípedo$P$ determinado por$v_1,v_2,\ldots,v_n\text{:}$

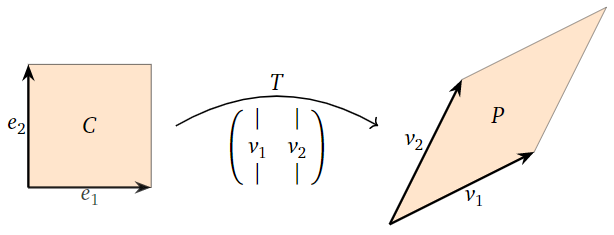
$clipboard_eedecb358654be10e0bfd9ded6b278c2c.png$

Figura$\PageIndex{18}$

Dado que el cubo unitario tiene volumen$1$ y su imagen tiene volumen,$|\det(A)|\text{,}$ la transformación$T$ escaló el volumen del cubo por un factor de$|\det(A)|$. Para replantear:

Nota$\PageIndex{1}$

Si$A$ es una$n\times n$ matriz con la transformación de matriz correspondiente$T\colon\mathbb{R}^n \to\mathbb{R}^n \text{,}$ y si$C$ es el cubo de la unidad en$\mathbb{R}^n \text{,}$ entonces el volumen de$T(C)$ es$|\det(A)|.$

La notación$T(S)$ significa la imagen de la región$S$ bajo la transformación$T$. En la notación del constructor de conjuntos, Nota 2.2.3 en la Sección 2.2, este es el subconjunto

\[ T(S) = \bigl\{T(x)\mid x \text{ in } S\bigr\}. \nonumber \]

De hecho,$T$ escala el volumen de cualquier región en$\mathbb{R}^n $ por el mismo factor, incluso para regiones con curvas.

Teorema $\PageIndex{2}$

Dejar$A$ ser una$n\times n$ matriz, y dejar$T\colon\mathbb{R}^n \to\mathbb{R}^n $ ser la transformación matricial asociada$T(x)=Ax$. Si$S$ hay alguna región en$\mathbb{R}^n \text{,}$ entonces

\[ \text{vol}(T(S))=|\det(A)|\cdot\text{vol}(S). \nonumber \]

Prueba

Dejar$C$ ser el cubo de la unidad, dejar$v_1,v_2,\ldots,v_n$ ser las columnas de$A\text{,}$ y dejar$P$ ser el paralellepipeado determinado por estos vectores, así$T(C) = P$ y$\text{vol}(P) = |\det(A)|$. Porque$\epsilon > 0$ dejamos$\epsilon C$ ser el cubo con longitudes laterales$\epsilon\text{,}$ es decir, el paralelepípedo determinado por los vectores$\epsilon e_1,\epsilon e_2,\ldots,\epsilon e_n\text{,}$ y definimos de$\epsilon P$ manera similar. Por la segunda propiedad definitoria,$T$ lleva$\epsilon C$ a$\epsilon P$. El volumen de$\epsilon C$ es$\epsilon^n$ (escalamos cada uno de los vectores$n$ estándar por un factor de$\epsilon$) y el volumen de$\epsilon P$ es$\epsilon^n|\det(A)|$ (por la misma razón), por lo que hemos demostrado que$T$ escala el volumen de$\epsilon C$ por$|\det(A)|$.

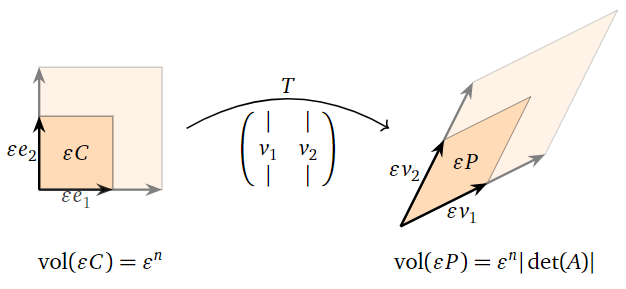
$clipboard_e5c48c9f5250c5dbbe9b2f31c21e4b457.png$

Figura$\PageIndex{19}$

Por la primera propiedad definitoria, Definición 3.3.1 en la Sección 3.3, la imagen de un traducir de$\epsilon C$ es una traducción de$\epsilon P\text{:}$

\[ T(x + \epsilon C) = T(x) + \epsilon T(C) = T(x) + \epsilon P. \nonumber \]

Dado que una traducción no cambia volúmenes, esto prueba que$T$ escala el volumen de una traducción de$\epsilon C$ por$|\det(A)|$.

En este punto, necesitamos utilizar técnicas a partir del cálculo multivariable, por lo que solo damos una idea del resto de la prueba. Cualquier región$S$ puede ser aproximada por una colección de cubos muy pequeños de la forma$x + \epsilon C$. La imagen$T(S)$ es entonces aproximada por la imagen de esta colección de cubos, que es una colección de paralelepípedos muy pequeños de la forma$T(x) + \epsilon P$.

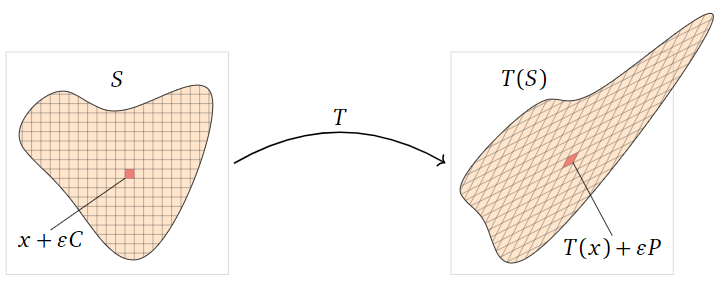
$clipboard_e11eba8c79aa78c611b71e5120509133b.png$

Figura$\PageIndex{20}$

El volumen de$S$ se aproxima estrechamente por la suma de los volúmenes de los cubos; de hecho, como$\epsilon$ va a cero, el límite de esta suma es precisamente$\text{vol}(S)$. De igual manera, el volumen de$T(S)$ es igual a la suma de los volúmenes de los paralelepípedos, tomar en el límite como$\epsilon\to 0$. El punto clave es que el volumen de cada cubo es escalado por$|\det(A)|$. Por lo tanto, la suma de los volúmenes de los paralelepípedos es$|\det(A)|$ por la suma de los volúmenes de los cubos. Esto demuestra que$\text{vol}(T(S)) = |\det(A)|\text{vol}(S).$

Ejemplo$\PageIndex{9}$

Dejar$S$ ser un semicírculo de radio$1\text{,}$ let

\[ A = \left(\begin{array}{cc}1&2\\2&1\end{array}\right), \nonumber \]

y definir$T\colon\mathbb{R}^2 \to\mathbb{R}^2 $ por$T(x)=Ax$. Cuál es el área de$T(S)\text{?}$

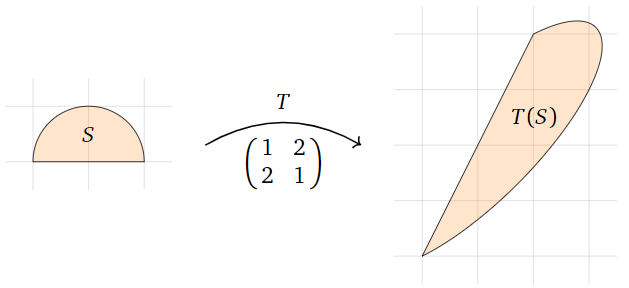
$clipboard_ec1847dde138b858fc1b133c6610ca44f.png$

Figura$\PageIndex{21}$

Solución

El área del círculo unitario es$\pi\text{,}$ así el área de$S$ es$\pi/2$. La transformación$T$ escala las áreas por un factor de$|\det(A)| = |1 - 4| = 3\text{,}$

\[ \text{vol}(T(S)) = 3\text{vol}(S) = \frac{3\pi}2. \nonumber \]

Ejemplo$\PageIndex{10}$: Area of an ellipse

Encuentra el área del interior$E$ de la elipse definida por la ecuación

\[ \left(\frac{2x-y}{2}\right)^2 + \left(\frac{y+3x}{3}\right)^2 = 1. \nonumber \]

Solución

Esta elipse se obtiene del círculo unitario$X^2+Y^2=1$ por el cambio lineal de coordenadas

\[ \begin{split} X \amp= \frac{2x-y}2 \\ Y \amp= \frac{y+3x}3. \end{split} \nonumber \]

En otras palabras, si definimos una transformación lineal$T\colon\mathbb{R}^2 \to\mathbb{R}^2 $ por

\[ T\left(\begin{array}{c}x\\y\end{array}\right) = \left(\begin{array}{c}(2x-y)/2 \\ (y+3x)/3\end{array}\right), \nonumber \]

luego$T{x\choose y}$ se encuentra en el círculo de la unidad$C$ cada vez que$x\choose y$ se encuentra$E$.

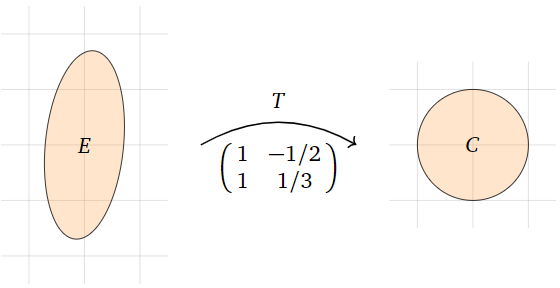
$clipboard_e842a398db5b34f989d7bc3b698a93289.png$

Figura$\PageIndex{22}$

Calculamos la matriz estándar$A$ para$T$ evaluando en los vectores de coordenadas estándar:

\[ T\left(\begin{array}{c}1\\0\end{array}\right) = \left(\begin{array}{c}1\\1\end{array}\right) \qquad T\left(\begin{array}{c}0\\1\end{array}\right) = \left(\begin{array}{c}-1/2 \\ 1/3\end{array}\right) \quad\implies\quad A = \left(\begin{array}{cc}1&-1/2 \\ 1&1/3\end{array}\right). \nonumber \]

Por lo tanto,$T$ escala las áreas por un factor de$|\det(A)| = |\frac13+\frac12| = \frac56.$ El área del círculo unitario es$\pi\text{,}$ tan

\[ \pi = \text{vol}(C) = \text{vol}(T(E)) = |\det(A)|\cdot\text{vol}(E) = \frac56\text{vol}(E), \nonumber \]

y así el área de$E$ es$6\pi/5$.

Observación: Multiplicatividad de$|\det|\,$

El teorema anterior$\PageIndex{2}$ también da una razón geométrica para la multiplicatividad del (valor absoluto del) determinante. En efecto, dejar$A$ y$B$ ser$n\times n$ matrices, y dejar que$T,U\colon\mathbb{R}^n \to\mathbb{R}^n $ sean las transformaciones matriciales correspondientes. Si$C$ es el cubo de la unidad, entonces

\[ \begin{split} \text{vol}\bigl(T\circ U(C)\bigr) = \text{vol}\bigl(T(U(C))\bigr) \amp= |\det(A)|\text{vol}(U(C)) \\ \amp= |\det(A)|\cdot|\det(B)|\text{vol}(C) \\ \amp= |\det(A)|\cdot|\det(B)|. \end{split} \nonumber \]

Por otro lado, la matriz para la composición$T\circ U$ es el producto$AB\text{,}$ así

\[ \text{vol}\bigl(T\circ U(C)\bigr) = |\det(AB)|\text{vol}(C) = |\det(AB)|. \nonumber \]

Así$|\det(AB)| = |\det(A)|\cdot|\det(B)|$.

Search

Definición\(\PageIndex{1}\): Paralellepiped

Ejemplo\(\PageIndex{1}\): The Unit Cubte

Ejemplo\(\PageIndex{2}\): Parallelograms

Ejemplo\(\PageIndex{3}\)

Observación Clave\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\): Determinants and Volumes

Ejemplo\(\PageIndex{4}\): Length

Ejemplo\(\PageIndex{5}\): Area

Ejemplo\(\PageIndex{6}\)

Solución

Ejemplo\(\PageIndex{7}\)

Solución

Ejemplo\(\PageIndex{8}\): Area of a triangle

Solución

Observación: Volúmenes firmados

Nota\(\PageIndex{1}\)

Teorema \(\PageIndex{2}\)

Ejemplo\(\PageIndex{9}\)

Solución

Ejemplo\(\PageIndex{10}\): Area of an ellipse

Solución

Observación: Multiplicatividad de\(|\det|\,\)