4.2: Expansiones de cofactores

\(\usepackage{macros} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Objetivos

1. Aprender a reconocer qué métodos son los más adecuados para calcular el determinante de una matriz dada.
2. Recetas: el determinante de una\(3\times 3\) matriz, computa el determinante usando expansiones de cofactores.
3. Palabras de vocabulario: menor, cofactor.

En esta sección, damos una fórmula recursiva para el determinante de una matriz, llamada expansión de cofactor. La fórmula es recursiva en que calcularemos el determinante de una\(n\times n\) matriz asumiendo que ya sabemos calcular el determinante de una\((n-1)\times(n-1)\) matriz.

Al final hay una subsección suplementaria sobre la regla de Cramer y una fórmula de cofactor para la inversa de una matriz.

Expansiones de cofactores

Una fórmula recursiva debe tener un punto de partida. Para las expansiones de cofactores, el punto de partida es el caso de\(1\times 1\) las matrices. La definición de determinante implica directamente que

\[ \det\left(\begin{array}{c}a\end{array}\right)=a. \nonumber \]

Para describir las expansiones de cofactores, necesitamos introducir alguna notación.

Definición\(\PageIndex{1}\): Minor and Cofactor

\(A\)Déjese ser una\(n\times n\) matriz.

1. El\((i,j)\) menor, denotado\(A_{ij}\text{,}\) es la\((n-1)\times (n-1)\) matriz obtenida a partir\(A\) de la eliminación de la fila\(i\) th y la\(j\) ésima columna.
2. El\((i,j)\) cofactor\(C_{ij}\) se define en términos del menor por\[C_{ij}=(-1)^{i+j}\det(A_{ij}).\nonumber\]

Tenga en cuenta que las señales de los cofactores siguen un “patrón de tablero de ajedrez”. A saber,\((-1)^{i+j}\) se representa en esta matriz:

\[\left(\begin{array}{cccc}\color{Green}{+}&\color{blue}{-}&\color{Green}{+}&\color{blue}{-} \\ \color{blue}{-}&\color{Green}{+}&\color{blue}{-}&\color{Green}{-} \\ \color{Green}{+}&\color{blue}{-}&\color{Green}{+}&\color{blue}{-} \\ \color{blue}{-}&\color{Green}{+}&\color{blue}{-}&\color{Green}{+}\end{array}\right).\nonumber\]

Ejemplo\(\PageIndex{1}\)

Para

\[ A= \left(\begin{array}{ccc}1&2&3\\4&5&6\\7&8&9\end{array}\right), \nonumber \]

\(A_{23}\)cómpiate y\(C_{23}.\)

Solución

Figura\(\PageIndex{1}\)

Los cofactores\(C_{ij}\) de una\(n\times n\) matriz son determinantes de\((n-1)\times(n-1)\) submatrices. De ahí que el siguiente teorema sea de hecho un procedimiento recursivo para computar el determinante.

Teorema\(\PageIndex{1}\): Cofactor Expansion

Dejar\(A\) ser una\(n\times n\) matriz con entradas\(a_{ij}\).

1. Para cualquiera\(i = 1,2,\ldots,n\text{,}\) que tengamos\[ \det(A) = \sum_{j=1}^n a_{ij}C_{ij} = a_{i1}C_{i1} + a_{i2}C_{i2} + \cdots + a_{in}C_{in}. \nonumber \] Esto se llama expansión de cofactor a lo largo de la fila\(i\) th.
2. Para cualquiera\(j = 1,2,\ldots,n\text{,}\) que tengamos\[ \det(A) = \sum_{i=1}^n a_{ij}C_{ij} = a_{1j}C_{1j} + a_{2j}C_{2j} + \cdots + a_{nj}C_{nj}. \nonumber \] Esto se llama expansión de cofactor a lo largo de la\(j\) th columna.

Prueba

Primero probaremos que la expansión del cofactor a lo largo de la primera columna calcula el determinante. Definir una función\(d\colon\{n\times n\text{ matrices}\}\to\mathbb{R}\)

\[ d(A) = \sum_{i=1}^n (-1)^{i+1} a_{i1}\det(A_{i1}). \nonumber \]

Eso queremos demostrarlo\(d(A) = \det(A)\). En lugar de mostrar que\(d\) satisface las cuatro propiedades definitorias del determinante, Definición 4.1.1, en la Sección 4.1, probaremos que satisface las tres propiedades definitorias alternativas, Observación: Propiedades definitorias alternativas, en la Sección 4.1, que fueron demostrado ser equivalente.

1. Afirmamos que\(d\) es multilineal en las filas de\(A\). Dejar\(A\) ser la matriz con filas\(v_1,v_2,\ldots,v_{i-1},v+w,v_{i+1},\ldots,v_n\text{:}\)\[A=\left(\begin{array}{ccc}a_11&a_12&a_13 \\ b_1+c_1 &b_2+c_2&b_3+c_3 \\ a_31&a_32&a_33\end{array}\right).\nonumber\] Aquí dejamos\(b_i\) y\(c_i\) ser las entradas de\(v\) y\(w\text{,}\) respectivamente. Dejar\(B\) y\(C\) ser las matrices con filas\(v_1,v_2,\ldots,v_{i-1},v,v_{i+1},\ldots,v_n\) y\(v_1,v_2,\ldots,v_{i-1},w,v_{i+1},\ldots,v_n\text{,}\) respectivamente:\[B=\left(\begin{array}{ccc}a_11&a_12&a_13\\b_1&b_2&b_3\\a_31&a_32&a_33\end{array}\right)\quad C=\left(\begin{array}{ccc}a_11&a_12&a_13\\c_1&c_2&c_3\\a_31&a_32&a_33\end{array}\right).\nonumber\] Deseamos mostrar\(d(A) = d(B) + d(C)\). Para\(i'\neq i\text{,}\) el\((i',1)\) -cofactor de\(A\) es la suma de los\((i',1)\) -cofactores de\(B\) y\(C\text{,}\) por multilinealidad de los determinantes de\((n-1)\times(n-1)\) matrices:\[ \begin{split} (-1)^{3+1}\det(A_{31}) \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\b_2+c_2&b_3+c_3\end{array}\right) \\ \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\b_2&b_3\end{array}\right) + (-1)^{3+1}\det\left(\begin{array}{cc}a_12&a_13\\c_2&c_3\end{array}\right) \\ \amp= (-1)^{3+1}\det(B_{31}) + (-1)^{3+1}\det(C_{31}). \end{split} \nonumber \] Por otro lado, los\((i,1)\) -cofactores de\(A,B,\) y\(C\) son todos iguales: \[ \begin{split} (-1)^{2+1} \det(A_{21}) \amp= (-1)^{2+1} \det\left(\begin{array}{cc}a_12&a_13\\a_32&a_33\end{array}\right) \\ \amp= (-1)^{2+1} \det(B_{21}) = (-1)^{2+1} \det(C_{21}). \end{split} \nonumber \]Ahora calculamos\[ \begin{split} d(A) \amp= (-1)^{i+1} (b_i + c_i)\det(A_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(A_{i'1}) \\ \amp= (-1)^{i+1} b_i\det(B_{i1}) + (-1)^{i+1} c_i\det(C_{i1}) \\ \amp\qquad\qquad+ \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\bigl(\det(B_{i'1}) + \det(C_{i'1})\bigr) \\ \amp= \left[(-1)^{i+1} b_i\det(B_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(B_{i'1})\right] \\ \amp\qquad\qquad+ \left[(-1)^{i+1} c_i\det(C_{i1}) + \sum_{i'\neq i} (-1)^{i'+1} a_{i1}\det(C_{i'1})\right] \\ \amp= d(B) + d(C), \end{split} \nonumber \] como se desee. Esto muestra que\(d(A)\) satisface la primera propiedad definitoria en las filas de\(A\).
   Todavía tenemos que demostrar que\(d(A)\) satisface la segunda propiedad definitoria en las filas de\(A\). \(B\)Sea la matriz obtenida escalando la fila\(i\) th de\(A\) por un factor de\(c\text{:}\)
   \[A=\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad B=\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\ca_{21}&ca_{22}&ca_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right).\nonumber\] Deseamos mostrar eso\(d(B) = c\,d(A)\). Para\(i'\neq i\text{,}\) el\((i',1)\) -cofactor de\(B\) es\(c\) veces el\((i',1)\) -cofactor de\(A\text{,}\) por multilinealidad de los determinantes de\((n-1)\times(n-1)\) -matrices:\[ \begin{split} (-1)^{3+1}\det(B_{31}) \amp= (-1)^{3+1}\det\left(\begin{array}{cc}a_{12}&a_{13}\\ca_{22}&ca_{23}\end{array}\right) \\ \amp= (-1)^{3+1}\cdot c\det\left(\begin{array}{cc}a_{12}&a_{13}\\a_{22}&a_{23}\end{array}\right) = (-1)^{3+1}\cdot c\det(A_{31}). \end{split} \nonumber \] Por otro lado, los\((i,1)\) -cofactores de\(A\) y\(B\) son los mismos:\[ (-1)^{2+1} \det(B_{21}) = (-1)^{2+1} \det\left(\begin{array}{cc}a_{12}&a_{13}\\a_{32}&a_{33}\end{array}\right) = (-1)^{2+1} \det(A_{21}). \nonumber \] Ahora nosotros computar\[ \begin{split} d(B) \amp= (-1)^{i+1}ca_{i1}\det(B_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1}\det(B_{i'1}) \\ \amp= (-1)^{i+1}ca_{i1}\det(A_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1}\cdot c\det(A_{i'1}) \\ \amp= c\left[(-1)^{i+1}ca_{i1}\det(A_{i1}) + \sum_{i'\neq i}(-1)^{i'+1} a_{i'1} \det(A_{i'1})\right] \\ \amp= c\,d(A), \end{split} \nonumber \] como se desee. Esto completa la prueba que\(d(A)\) es multilineal en las filas de\(A\).
2. Ahora mostramos que\(d(A) = 0\) si\(A\) tiene dos filas idénticas. Supongamos que las filas\(i_1,i_2\) de\(A\) son idénticas, con\(i_1 \lt i_2\text{:}\)\[A=\left(\begin{array}{cccc}a_{11}&a_{12}&a_{13}&a_{14}\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{11}&a_{12}&a_{13}&a_{14}\end{array}\right).\nonumber\] Si\(i\neq i_1,i_2\) entonces el\((i,1)\) -cofactor de\(A\) es igual a cero, ya que\(A_{i1}\) es una\((n-1)\times(n-1)\) matriz con filas idénticas:\[ (-1)^{2+1}\det(A_{21}) = (-1)^{2+1} \det\left(\begin{array}{ccc}a_{12}&a_{13}&a_{14}\\a_{32}&a_{33}&a_{34}\\a_{12}&a_{13}&a_{14}\end{array}\right) = 0. \nonumber \] El\((i_1,1)\) -menor se puede transformar en el\((i_2,1)\) - menor usando swaps de\(i_2 - i_1 - 1\) filas:

Figura\(\PageIndex{2}\)

2. Por lo tanto,\[ (-1)^{i_1+1}\det(A_{i_11}) = (-1)^{i_1+1}\cdot(-1)^{i_2 - i_1 - 1}\det(A_{i_21}) = -(-1)^{i_2+1}\det(A_{i_21}). \nonumber \] los dos cofactores restantes se cancelan, así\(d(A) = 0\text{,}\) como se desee.
3. Queda por demostrarlo\(d(I_n) = 1\). El primero es el único término distinto de cero en la expansión del cofactor de la identidad:\[ d(I_n) = 1\cdot(-1)^{1+1}\det(I_{n-1}) = 1. \nonumber \]

Esto demuestra que\(\det(A) = d(A)\text{,}\) es decir, que la expansión del cofactor a lo largo de la primera columna calcula el determinante.

Ahora mostramos que la expansión del cofactor a lo largo de la columna\(j\) th también calcula el determinante. Al realizar swaps de\(j-1\) columna, se puede mover la\(j\) ésima columna de una matriz a la primera columna, manteniendo las otras columnas en orden. Por ejemplo, aquí movemos la tercera columna a la primera, usando dos swaps de columnas:

Figura\(\PageIndex{3}\)

Dejar\(B\) ser la matriz obtenida moviendo la\(j\) th columna de\(A\) a la primera columna de esta manera. Entonces el\((i,j)\) menor\(A_{ij}\) es igual al\((i,1)\) menor\(B_{i1}\text{,}\) ya que eliminar la\(i\) th columna de\(A\) es lo mismo que eliminar la primera columna de\(B\). Por construcción, la\((i,j)\) -entrada\(a_{ij}\) de\(A\) es igual a la\((i,1)\) -entrada\(b_{i1}\) de\(B\). Como sabemos que podemos calcular determinantes expandiéndonos a lo largo de la primera columna, tenemos

\[ \det(B) = \sum_{i=1}^n (-1)^{i+1} b_{i1}\det(B_{i1}) = \sum_{i=1}^n (-1)^{i+1} a_{ij}\det(A_{ij}). \nonumber \]

Ya que\(B\) se obtuvo a partir\(A\) de la realización de swaps de\(j-1\) columna, tenemos

\[ \begin{split} \det(A) = (-1)^{j-1}\det(B) \amp= (-1)^{j-1}\sum_{i=1}^n (-1)^{i+1} a_{ij}\det(A_{ij}) \\ \amp= \sum_{i=1}^n (-1)^{i+j} a_{ij}\det(A_{ij}). \end{split} \nonumber \]

Esto demuestra que la expansión del cofactor a lo largo de la columna\(i\) th calcula el determinante de\(A\).

Por la propiedad de transposición, Proposición 4.1.4 en la Sección 4.1, la expansión del cofactor a lo largo de la fila\(i\) th de\(A\) es la misma que la expansión del cofactor a lo largo de la\(i\) th columna de\(A^T\). Nuevamente por la propiedad de transposición, tenemos\(\det(A)=\det(A^T)\text{,}\) así que expandiendo cofactores a lo largo de una fila también calcula el determinante.

Tenga en cuenta que el teorema en realidad da\(2n\) diferentes fórmulas para el determinante: una para cada fila y otra para cada columna. Por ejemplo, la fórmula para la expansión del cofactor a lo largo de la primera columna es

\[ \begin{split} \det(A) = \sum_{i=1}^n a_{i1}C_{i1} \amp= a_{11}C_{11} + a_{21}C_{21} + \cdots + a_{n1}C_{n1} \\ \amp= a_{11}\det(A_{11}) - a_{21}\det(A_{21}) + a_{31}\det(A_{31}) - \cdots \pm a_{n1}\det(A_{n1}). \end{split} \nonumber \]

Recuerde, el determinante de una matriz es solo un número, definido por las cuatro propiedades definitorias, Definición 4.1.1 en la Sección 4.1, así que para ser claros:

Nota\(\PageIndex{1}\)

Se obtiene el mismo número expandiendo cofactores a lo largo de\(any\) fila o columna.

Ahora que tenemos una fórmula recursiva para el determinante, finalmente podemos probar el teorema de la existencia, Teorema 4.1.1 en la Sección 4.1.

Prueba

Revisemos lo que realmente probamos en la Sección 4.1. Mostramos que si\(\det\colon\{n\times n\text{ matrices}\}\to\mathbb{R}\) alguna función satisface las cuatro propiedades definitorias del determinante, Definición 4.1.1 en la Sección 4.1, (o las tres propiedades definitorias alternativas, Observación: Propiedades definitorias alternativas,), entonces también satisface todas las propiedades maravillosas probado en esa sección. En particular, dado que se\(\det\) puede calcular usando la reducción de fila por Receta: Computación de Determinantes por Reducción de Fila, se caracteriza de manera única por las propiedades definitorias. Lo que no probamos fue la existencia de tal función, ya que no sabíamos que dos procedimientos diferentes de reducción de filas siempre computarían la misma respuesta.

Considere la función\(d\) definida por la expansión del cofactor a lo largo de la primera fila:

\[ d(A) = \sum_{i=1}^n (-1)^{i+1} a_{i1}\det(A_{i1}). \nonumber \]

Si asumimos que el determinante existe para\((n-1)\times(n-1)\) las matrices, entonces no hay duda de que la función\(d\) existe, ya que le dimos una fórmula para ello. Además, mostramos en la prueba del Teorema\(\PageIndex{1}\) anterior que\(d\) satisface las tres propiedades definitorias alternativas del determinante, nuevamente solo asumiendo que el determinante existe para\((n-1)\times(n-1)\) matrices. ¡Esto prueba la existencia del determinante para\(n\times n\) las matrices!

Este es un ejemplo de una prueba por inducción matemática. Comenzamos notando que\(\det\left(\begin{array}{c}a\end{array}\right) = a\) satisface las cuatro propiedades definitorias del determinante de una\(1\times 1\) matriz. Luego mostramos que existe el determinante de\(n\times n\) las matrices, asumiendo que existe el determinante de\((n-1)\times(n-1)\) las matrices. Esto implica que todos los determinantes existen, por la siguiente cadena de lógica:

\[ 1\times 1\text{ exists} \;\implies\; 2\times 2\text{ exists} \;\implies\; 3\times 3\text{ exists} \;\implies\; \cdots. \nonumber \]

Ejemplo\(\PageIndex{2}\)

Encuentra el determinante de

\[ A= \left(\begin{array}{ccc}2&1&3\\-1&2&1\\-2&2&3\end{array}\right). \nonumber \]

Solución

Hacemos la elección un tanto arbitraria de expandirnos a lo largo de la primera fila. Los menores y cofactores son

Figura\(\PageIndex{4}\)

Por lo tanto,

\[ \det(A)=a_{11}C_{11}+a_{12}C_{12}+a_{13}C_{13} =(2)(4)+(1)(1)+(3)(2)=15. \nonumber \]

Ejemplo\(\PageIndex{3}\): The Determinant of a \(2\times 2\) Matrix

Calculemos (de nuevo) el determinante de una\(2\times2\) matriz general

\[ A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right). \nonumber \]

Los menores son

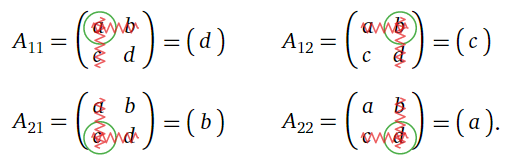
Figura\(\PageIndex{5}\)

Los menores son todas\(1\times 1\) matrices. Como hemos visto que el determinante de una\(1\times1\) matriz es solo el número dentro de ella, los cofactores son por lo tanto

\ begin {align*} C_ {11} &= {+\ det (A_ {11}) = d} & C_ {12} &= {-\ det (A_ {12}) = -c}\\ C_ {21} &= {-\ det (A_ {21}) = -b} & C_ {22} &= {+\ det (A_ {22}) = a}\ end {alinear*}

Ampliando los cofactores a lo largo de la primera columna, encontramos que

\[ \det(A)=aC_{11}+cC_{21} = ad - bc, \nonumber \]

que concuerda con las fórmulas de la Definición 3.5.2 en la Sección 3.5 y en el Ejemplo 4.1.6 en la Sección 4.1.

Ejemplo\(\PageIndex{4}\): The Determinant of a \(3\times 3\) Matrix

También podemos usar expansiones de cofactores para encontrar una fórmula para el determinante de una\(3\times 3\) matriz. Vamos a calcular el determinante de

\[ A = \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right) \nonumber \]

expandiéndose a lo largo de la primera fila. Los menores y cofactores son:

Figura\(\PageIndex{6}\)

El determinante es:

\ begin {alinear*}\ det (A)\ amp= a_ {11} C_ {11} + a_ {12} C_ {12} + a_ {13} C_ {13}\\ amp = a_ {11}\ det\ left (\ begin {array} {cc} a_ {22} &a_ {23}\\ a_ {32} &a_ {33} end {array}\ right) - a_ {12}\ det\ left (\ begin {array} {cc} a_ {21} &a_ {23}\\ a_ {31} &a_ {33}\ end {array}\ derecha) + a_ {13}\ det\ left (\ begin {array} {cc} a_ {21} &a_ {22}\\ a_ {31} &a_ {32}\ end {array}\\ derecha)\\ amp= a_ {11} (a_ {22} a_ {33} -a_ {23} a_ {32}) - a_ {12} (a_ {21} a_ {33} -a_ {23} a_ {31}) + a_ {13} (a_ {21} a_ {32} -a_ {22} a_ {31})\\ amp= a_ {11} a_ {22} a_ {33} + a_ {12} a_ {23} a_ {31} + a_ {13} a_ {21} a_ {32} -a_ {13} a_ {22} a_ {31} - a_ {11} a_ {23} _ {32} - a_ {12} a_ {21} a_ {33}. \ end {alinear*}

La fórmula para el determinante de una\(3\times 3\) matriz parece demasiado complicada de memorizar directamente. Afortunadamente, existe el siguiente dispositivo mnemotécnico.

Receta: Computar el Determinante de un\(3\times 3\) Matrix

Para calcular el determinante de una\(3\times 3\) matriz, primero dibuje una matriz más grande con las dos primeras columnas repetidas a la derecha. Luego suma los productos de las diagonales descendentes y resta los productos de las diagonales ascendentes:

\[\det\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)=\begin{array}{l} \color{Green}{a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}} \\ \color{blue}{\quad -a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33}}\end{array} \nonumber\]

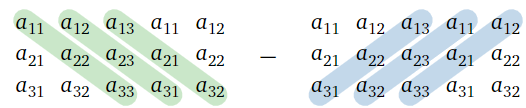
Figura\(\PageIndex{7}\)

Alternativamente, no es necesario repetir las dos primeras columnas si permites que tus diagonales “envuelvan” los lados de una matriz, como en Pac-Man o Asteroides.

Ejemplo\(\PageIndex{5}\)

Encuentra el determinante de\(A=\left(\begin{array}{ccc}1&3&5\\2&0&-1\\4&-3&1\end{array}\right)\).

Solución

Repetimos las dos primeras columnas a la derecha, luego sumamos los productos de las diagonales descendentes y restamos los productos de las diagonales ascendentes:

Figura\(\PageIndex{8}\)

\[\det\left(\begin{array}{ccc}1&3&5\\2&0&-1\\4&-3&1\end{array}\right)=\begin{array}{l}\color{Green}{(1)(0)(1)+(3)(-1)(4)+(5)(2)(-3)} \\ \color{blue}{\quad -(5)(0)(4)-(1)(-1)(-3)-(3)(2)(1)}\end{array} =-51.\nonumber\]

Las expansiones de cofactores son más útiles a la hora de calcular el determinante de una matriz que tiene una fila o columna con varias entradas cero. En efecto, si la\((i,j)\) entrada de\(A\) es cero, entonces no hay razón para computar el\((i,j)\) cofactor. En el siguiente ejemplo calculamos el determinante de una matriz con dos ceros en la cuarta columna expandiendo cofactores a lo largo de la cuarta columna.

Ejemplo\(\PageIndex{6}\)

Encuentra el determinante de

\[ A= \left(\begin{array}{cccc}2&5&-3&-2\\-2&-3&2&-5\\1&3&-2&0\\-1&6&4&0\end{array}\right). \nonumber \]

Solución

La cuarta columna tiene dos entradas cero. Nos expandimos a lo largo de la cuarta columna para encontrar

\[ \begin{split} \det(A) \amp= 2\det\left(\begin{array}{ccc}-2&-3&2\\1&3&-2\\-1&6&4\end{array}\right) -5 \det \left(\begin{array}{ccc}2&5&-3\\1&3&-2\\-1&6&4\end{array}\right) \\ \amp\qquad - 0\det(\text{don't care}) + 0\det(\text{don't care}). \end{split} \nonumber \]

Sólo tenemos que computar dos cofactores. Podemos encontrar estos determinantes usando cualquier método que queramos; en aras de la ilustración, ampliaremos los cofactores en uno y usaremos la fórmula para el\(3\times 3\) determinante en el otro.

Expandiendo a lo largo de la primera columna, calculamos

\ begin {align*} &\ det\ left (\ begin {array} {ccc} -2&-3&2\\ 1&3&-2\\ -1&6&4\ end {array}\ right)\\ &\ quad= -2\ det\ left (\ begin {array} {cc} 3&-2\ 6&4\ end {array}\ right) -\ det\ left (\ begin {array} {cc} -3&2\\ 6&4\ end {array}\ derecha) -\ det\ left (\ begin {array} {cc} -3&2\ 3&-2\ end {array}\ right)\\ &\ quad= -2 (24) - (-24) -0=-48+24+0=-24. \ end {alinear*}

Usando la fórmula para el\(3\times 3\) determinante, tenemos

\[\det\left(\begin{array}{ccc}2&5&-3\\1&3&-2\\-1&6&4\end{array}\right)=\begin{array}{l}\color{Green}{(2)(3)(4) + (5)(-2)(-1)+(-3)(1)(6)} \\ \color{blue}{\quad -(2)(-2)(6)-(5)(1)(4)-(-3)(3)(-1)}\end{array} =11.\nonumber\]

Así, encontramos que

\[ \det(A)= 2(-24)-5(11)=-103. \nonumber \]

Las expansiones de cofactores también son muy útiles a la hora de calcular el determinante de una matriz con entradas desconocidas. En efecto, es inconveniente reducir filas en este caso, porque no se puede estar seguro de si una entrada que contiene un desconocido es un pivote o no.

Ejemplo\(\PageIndex{7}\)

Calcular el determinante de esta matriz que contiene lo desconocido\(\lambda\text{:}\)

\[A=\left(\begin{array}{cccc}-\lambda&2&7&12\\3&1-\lambda&2&-4\\0&1&-\lambda&7\\0&0&0&2-\lambda\end{array}\right).\nonumber\]

Solución

Primero expandimos los cofactores a lo largo de la cuarta fila:

\[ \begin{split} \det(A) \amp= 0\det\left(\begin{array}{c}\cdots\end{array}\right) + 0\det\left(\begin{array}{c}\cdots\end{array}\right) + 0\det\left(\begin{array}{c}\cdots\end{array}\right) \\ \amp\qquad+ (2-\lambda)\det\left(\begin{array}{ccc}-\lambda&2&7\\3&1-\lambda &2\\0&1&-\lambda\end{array}\right). \end{split} \nonumber \]

Sólo tenemos que computar un cofactor. Para ello, primero limpiamos la\((3,3)\) entrada mediante la realización del reemplazo de columna\(C_3 = C_3 + \lambda C_2\text{,}\) que no cambia el determinante:

\[ \det\left(\begin{array}{ccc}-\lambda&2&7\\3&1-\lambda &2\\0&1&-\lambda\end{array}\right) = \det\left(\begin{array}{ccc}-\lambda&2&7+2\lambda \\ 3&1-\lambda&2+\lambda(1-\lambda) \\ 0&1&0\end{array}\right). \nonumber \]

Ahora ampliamos cofactores a lo largo de la tercera fila para encontrar

\[ \begin{split} \det\left(\begin{array}{ccc}-\lambda&2&7+2\lambda \\ 3&1-\lambda&2+\lambda(1-\lambda) \\ 0&1&0\end{array}\right) \amp= (-1)^{2+3}\det\left(\begin{array}{cc}-\lambda&7+2\lambda \\ 3&2+\lambda(1-\lambda)\end{array}\right) \\ \amp= -\biggl(-\lambda\bigl(2+\lambda(1-\lambda)\bigr) - 3(7+2\lambda) \biggr) \\ \amp= -\lambda^3 + \lambda^2 + 8\lambda + 21. \end{split} \nonumber \]

Por lo tanto, tenemos

\[ \det(A) = (2-\lambda)(-\lambda^3 + \lambda^2 + 8\lambda + 21) = \lambda^4 - 3\lambda^3 - 6\lambda^2 - 5\lambda + 42. \nonumber \]

A menudo es más eficiente utilizar una combinación de varias técnicas al computar el determinante de una matriz. De hecho, al expandir cofactores en una matriz, se pueden calcular los determinantes de los cofactores de la manera que sea más conveniente. O bien, se pueden realizar operaciones de fila y columna para borrar algunas entradas de una matriz antes de expandir cofactores, como en el ejemplo anterior.

Nota\(\PageIndex{2}\): Summary: Methods for Computing Determinants

Tenemos varias formas de calcular determinantes:

1. Fórmulas especiales para\(2\times 2\) y\(3\times 3\) matrices.
   Esta suele ser la mejor manera de calcular el determinante de una matriz pequeña, a excepción de una\(3\times 3\) matriz con varias entradas cero.
2. Expansión de cofactores.
   Esto suele ser más eficiente cuando hay una fila o columna con varias entradas cero, o si la matriz tiene entradas desconocidas.
3. Operaciones de fila y columna.
   Este es generalmente el más rápido cuando se presenta con una matriz grande que no tiene una fila o columna con muchos ceros en ella.
4. Cualquier combinación de lo anterior.
   La expansión del cofactor es recursiva, pero se pueden calcular los determinantes de los menores usando cualquier método que sea más conveniente. O bien, puede realizar operaciones de fila y columna para borrar algunas entradas de una matriz antes de expandir cofactores.

Recuerde, todos los métodos para computar el determinante producen el mismo número.

La regla de Cramer y la matriz se invierte

Recordemos de la Proposición 3.5.1 en la Sección 3.5 que se puede calcular el determinante de una\(2\times 2\) matriz usando la regla

\[ A = \left(\begin{array}{cc}d&-b\\-c&a\end{array}\right) \quad\implies\quad A^{-1} = \frac 1{\det(A)}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right). \nonumber \]

Calculamos los cofactores de una\(2\times 2\) matriz en Ejemplo\(\PageIndex{3}\); usando\(C_{11}=d,\,C_{12}=-c,\,C_{21}=-b,\,C_{22}=a\text{,}\) podemos reescribir la fórmula anterior como

\[ A^{-1} = \frac 1{\det(A)}\left(\begin{array}{cc}C_{11}&C_{21}\\C_{12}&C_{22}\end{array}\right). \nonumber \]

Resulta que esta fórmula generaliza a\(n\times n\) matrices.

Teorema\(\PageIndex{2}\)

Dejar\(A\) ser una\(n\times n\) matriz invertible, con cofactores\(C_{ij}\). Entonces

\[\label{eq:1}A^{-1}=\frac{1}{\det (A)}\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots&C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots&\vdots &\ddots&\vdots&\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C_{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right).\]

La matriz de cofactores a veces se llama la matriz yugada de\(A\text{,}\) y se denota\(\text{adj}(A)\text{:}\)

\[\text{adj}(A)=\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots &C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots&\vdots&\ddots&\vdots&\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C_{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right).\nonumber\]

Obsérvese que el\((i,j)\) cofactor\(C_{ij}\) va en la\((j,i)\) entrada la matriz yugada, no la\((i,j)\) entrada: la matriz adyugada es la transposición de la matriz del cofactor.

Observación

De hecho, siempre se tiene\(A\cdot\text{adj}(A) = \text{adj}(A)\cdot A = \det(A)I_n,\) si\(A\) es o no invertible.

Ejemplo\(\PageIndex{8}\)

Usa el Teorema\(\PageIndex{2}\) para calcular\(A^{-1}\text{,}\) dónde

\[ A = \left(\begin{array}{ccc}1&0&1\\0&1&1\\1&1&0\end{array}\right). \nonumber \]

Solución

Los menores de edad son:

\[\begin{array}{lllll}A_{11}=\left(\begin{array}{cc}1&1\\1&0\end{array}\right)&\quad&A_{12}=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)&\quad&A_{13}=\left(\begin{array}{cc}0&1\\1&1\end{array}\right) \\ A_{21}=\left(\begin{array}{cc}0&1\\1&0\end{array}\right)&\quad&A_{22}=\left(\begin{array}{cc}1&1\\1&0\end{array}\right)&\quad&A_{23}=\left(\begin{array}{cc}1&0\\1&1\end{array}\right) \\ A_{31}=\left(\begin{array}{cc}0&1\\1&1\end{array}\right)&\quad&A_{32}=\left(\begin{array}{cc}1&1\\0&1\end{array}\right)&\quad&A_{33}=\left(\begin{array}{cc}1&0\\0&1\end{array}\right)\end{array}\nonumber\]

Los cofactores son:

\[\begin{array}{lllll}C_{11}=-1&\quad&C_{12}=1&\quad&C_{13}=-1 \\ C_{21}=1&\quad&C_{22}=-1&\quad&C_{23}=-1 \\ C_{31}=-1&\quad&C_{32}=-1&\quad&C_{33}=1\end{array}\nonumber\]

Al expandirse a lo largo de la primera fila, calculamos el determinante para ser

\[ \det(A) = 1\cdot C_{11} + 0\cdot C_{12} + 1\cdot C_{13} = -2. \nonumber \]

Por lo tanto, lo inverso es

\[ A^{-1} = \frac 1{\det(A)} \left(\begin{array}{ccc}C_{11}&C_{21}&C_{31}\\C_{12}&C_{22}&C_{32}\\C_{13}&C_{23}&C_{33}\end{array}\right) = -\frac12\left(\begin{array}{ccc}-1&1&-1\\1&-1&-1\\-1&-1&1\end{array}\right). \nonumber \]

Se desprende del ejemplo anterior que\(\eqref{eq:1}\) es una forma muy ineficiente de computar la inversa de una matriz, en comparación con el aumento por la matriz de identidad y la reducción de filas, como en la Subsección Computación de la Matriz Inversa en la Sección 3.5. Sin embargo, tiene sus usos.

• Si una matriz tiene entradas desconocidas, entonces es difícil calcular su inversa usando la reducción de filas, por la misma razón es difícil calcular el determinante de esa manera: no se puede estar seguro de si una entrada que contiene un desconocido es un pivote o no.
• Esta fórmula es útil para fines teóricos. Observe que los únicos denominadores en\(\eqref{eq:1}\) ocurren al dividir por el determinante: computar cofactores sólo implica multiplicación y suma, nunca división. Esto significa, por ejemplo, que si el determinante es muy pequeño, entonces cualquier error de medición en las entradas de la matriz se magnifica mucho al calcular la inversa. De esta manera,\(\eqref{eq:1}\) es útil en el análisis de errores.

La prueba del Teorema\(\PageIndex{2}\) utiliza un interesante truco llamado Regla de Cramer, que da una fórmula para las entradas de la solución de una ecuación matricial invertible.

Teorema\(\PageIndex{3}\): Cramer's Rule

Dejar\(x = (x_1,x_2,\ldots,x_n)\) ser la solución de\(Ax=b\text{,}\) donde\(A\) es una\(n\times n\) matriz invertible y\(b\) es un vector en\(\mathbb{R}^n \). Dejar\(A_i\) ser la matriz obtenida de\(A\) reemplazando la\(i\) th columna por\(b\). Entonces

\[ x_i = \frac{\det(A_i)}{\det(A)}. \nonumber \]

Prueba

Primero supongamos que esa\(A\) es la matriz de identidad, así que eso\(x = b\). Entonces la matriz\(A_i\) se ve así:

\[ \left(\begin{array}{cccc}1&0&b_1&0\\0&1&b_2&0\\0&0&b_3&0\\0&0&b_4&1\end{array}\right). \nonumber \]

Ampliando cofactores a lo largo de la fila\(i\) th, vemos que\(\det(A_i)=b_i\text{,}\) así en este caso,

\[ x_i = b_i = \det(A_i) = \frac{\det(A_i)}{\det(A)}. \nonumber \]

Ahora\(A\) déjese ser una\(n\times n\) matriz general. Una forma de resolver\(Ax=b\) es remar reducir la matriz aumentada\((\,A\mid b\,)\text{;}\) el resultado es\((\,I_n\mid x\,).\) Por el caso que manejamos anteriormente, basta con comprobar que la cantidad\(\det(A_i)/\det(A)\) no cambia cuando hacemos una operación de fila a\((\,A\mid b\,)\text{,}\) desde\(\det(A_i)/\det(A) = x_i\) cuando\(A = I_n\).

1. Hacer un reemplazo de fila en\((\,A\mid b\,)\) hace el mismo reemplazo de fila una\(A\) y otra vez\(A_i\text{:}\)
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{lll|l}a_{11}&a_{12}&a_{13}&b_1\\ a_{21}-2a_{31}&a_{22}-2a_{32}&a_{23}-2a_{33}&b_2-2b_3 \\ a_{31}&a_{32}&a_{33}&b_3 \end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad \xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13} \\ a_{21}-2a_{31}&a_{22}-2a_{32}&a_{23}-2a_{33} \\ a_{31}&a_{32}&a_{33}\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad \xrightarrow{R_2=R_2-2R_3}\quad&\left(\begin{array}{ccc}a_{11}&b_{1}&a_{13} \\ a_{21}-2a_{31}&b_{2}-2b_{3}&a_{23}-2a_{33} \\ a_{31}&b_{3}&a_{33}\end{array}\right).\end{aligned}\]
   En particular,\(\det(A)\) y no\(\det(A_i)\) cambian, por lo\(\det(A)/\det(A_i)\) que no cambia.
2. Escalar una fila de\((\,A\mid b\,)\) por un factor de\(c\) escala la misma fila de\(A\) y de\(A_i\) por el mismo factor:
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}&b_1 \\ ca_{21}&ca_{22}&ca_{23}&cb_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\ca_{21}&ca_{22}&ca_{23} \\ a_{31}&a_{32}&a_{33}\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad\xrightarrow{R_2=cR_2}\quad&\left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\ca_{21}&cb_{2}&ca_{23} \\ a_{31}&b_{3}&a_{33}\end{array}\right).\end{aligned}\]
   En particular,\(\det(A)\) y ambos\(\det(A_i)\) se escalan por un factor de\(c\text{,}\) así no\(\det(A_i)/\det(A)\) se modifica.
3. Intercambiando dos filas de\((\,A\mid b\,)\) swaps las mismas filas de\(A\) y de\(A_i\text{:}\)
   \[\begin{aligned}\left(\begin{array}{ccc|c}a_{11}&a_{12}&a_{13}&b_1 \\ a_{21}&a_{22}&a_{23}&b_2\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc|c}a_{21}&a_{22}&a_{23}&b_2\\a_{11}&a_{12}&a_{13}&b_1\\a_{31}&a_{32}&a_{33}&b_3\end{array}\right) \\ \left(\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc}a_{21}&a_{22}&a_{23}\\a_{11}&a_{12}&a_{13}\\a_{31}&a_{32}&a_{33}\end{array}\right) \\  \left(\begin{array}{ccc}a_{11}&b_{1}&a_{13}\\a_{21}&b_{2}&a_{23}\\a_{31}&b_{3}&a_{33}\end{array}\right)\quad\xrightarrow{R_1\longleftrightarrow R_2}\quad&\left(\begin{array}{ccc}a_{21}&b_2&a_{23} \\ a_{11}&b_1&a_{13}\\a_{31}&b_3&a_{33}\end{array}\right).\end{aligned}\]
   En particular,\(\det(A)\) y ambas\(\det(A_i)\) son negadas, por lo que no\(\det(A_i)/\det(A)\) se modifica.

Ejemplo\(\PageIndex{9}\)

Calcular la solución de\(Ax=b\) usar la regla de Cramer, donde

\[ A = \left(\begin{array}{cc}a&b\\c&d\end{array}\right) \qquad b = \left(\begin{array}{c}1\\2\end{array}\right). \nonumber \]

Aquí los coeficientes de\(A\) son desconocidos, pero\(A\) pueden suponerse invertibles.

Solución

Primero calculamos los determinantes de las matrices obtenidas reemplazando las columnas\(A\) de por\(b\text{:}\)

\[\begin{array}{lll}A_1=\left(\begin{array}{cc}1&b\\2&d\end{array}\right)&\qquad&\det(A_1)=d-2b \\ A_2=\left(\begin{array}{cc}a&1\\c&2\end{array}\right)&\qquad&\det(A_2)=2a-c.\end{array}\nonumber\]

Ahora calculamos

\[ \frac{\det(A_1)}{\det(A)} = \frac{d-2b}{ad-bc} \qquad \frac{\det(A_2)}{\det(A)} = \frac{2a-c}{ad-bc}. \nonumber \]

De ello se deduce que

\[ x = \frac 1{ad-bc}\left(\begin{array}{c}d-2b\\2a-c\end{array}\right). \nonumber \]

Ahora usamos la regla de Cramer para probar el primer Teorema\(\PageIndex{2}\) de esta subsección.

Prueba

La columna\(j\) th de\(A^{-1}\) es\(x_j = A^{-1} e_j\). Este vector es la solución de la ecuación matricial

\[ Ax = A\bigl(A^{-1} e_j\bigr) = I_ne_j = e_j. \nonumber \]

Por regla de Cramer, la entrada\(i\) th de\(x_j\)\(A_i\) es\(\det(A_i)/\det(A)\text{,}\) donde se obtiene la matriz\(A\) reemplazando la\(i\) th columna de\(A\) por\(e_j\text{:}\)

\[A_i=\left(\begin{array}{cccc}a_{11}&a_{12}&0&a_{14}\\a_{21}&a_{22}&1&a_{24}\\a_{31}&a_{32}&0&a_{34}\\a_{41}&a_{42}&0&a_{44}\end{array}\right)\quad (i=3,\:j=2).\nonumber\]

Expandiendo cofactores a lo largo de la columna\(i\) th, vemos que el determinante de\(A_i\) es exactamente el\((j,i)\) -cofactor\(C_{ji}\) de\(A\). Por lo tanto, la columna\(j\) th de\(A^{-1}\) es

\[ x_j = \frac 1{\det(A)}\left(\begin{array}{c}C_{ji}\\C_{j2}\\ \vdots \\ C_{jn}\end{array}\right), \nonumber \]

y por lo tanto

\[ A^{-1} = \left(\begin{array}{cccc}|&|&\quad&| \\ x_1&x_2&\cdots &x_n\\ |&|&\quad &|\end{array}\right) = \frac 1{\det(A)}\left(\begin{array}{ccccc}C_{11}&C_{21}&\cdots &C_{n-1,1}&C_{n1} \\ C_{12}&C_{22}&\cdots &C_{n-1,2}&C_{n2} \\ \vdots &\vdots &\ddots &\vdots &\vdots \\ C_{1,n-1}&C_{2,n-1}&\cdots &C_{n-1,n-1}&C{n,n-1} \\ C_{1n}&C_{2n}&\cdots &C_{n-1,n}&C_{nn}\end{array}\right). \nonumber \]