6.4: Conjuntos ortogonales

Objetivos de aprendizaje

1. Entender cuál es el mejor método para calcular una proyección ortogonal en una situación dada.
2. Recetas: un conjunto ortonormal de un conjunto ortogonal, Fórmula de proyección, coordenadas B cuando B es un conjunto ortogonal, proceso Gram—Schmidt.
3. Palabras de vocabulario: conjunto ortogonal, conjunto ortonormal.

En esta sección, damos una fórmula para proyección ortogonal que es considerablemente más simple que la de la Sección 6.3, en el sentido de que no requiere reducción de filas ni inversión matricial. Sin embargo, esta fórmula, llamada Fórmula de Proyección, sólo funciona en presencia de una base ortogonal. También presentaremos el proceso Gram—Schmidt para convertir una base arbitraria en una ortogonal.

Conjuntos ortogonales y la fórmula de proyección

Los cálculos que involucran proyecciones tienden a ser mucho más fáciles en presencia de un conjunto ortogonal de vectores.

Definición\(\PageIndex{1}\): Orthogonal and Orthonormal

Un conjunto de vectores distintos de cero\(\{u_1,\: u_2,\cdots ,u_m\}\) se llama ortogonal si\(u_i\cdot u_j=0\) siempre\(i\neq j\). Es ortonormal si es ortogonal, y además\(u_i\cdot u_i=1\) para todos\(i=1,\: 2,\cdots ,m\).

En otras palabras, un conjunto de vectores es ortogonal si diferentes vectores en el conjunto son perpendiculares entre sí. Un conjunto ortonormal es un conjunto ortogonal de vectores unitarios, Definición 6.1.3 en la Sección 6.1.

Ejemplo\(\PageIndex{1}\)

Los vectores de coordenadas estándar\(\mathbb{R}^n\) siempre forman un conjunto ortonormal. Por ejemplo, en\(\mathbb{R}^3\) comprobamos que

\[\left(\begin{array}{c}1\\0\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\1\\0\end{array}\right)=0\quad\left(\begin{array}{c}1\\0\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)=0\quad\left(\begin{array}{c}0\\1\\0\end{array}\right)\cdot\left(\begin{array}{c}0\\0\\1\end{array}\right)=0.\nonumber\]

Ya que\(e_i\cdot e_i=1\) para todos\(i=1,\: 2,\:3\), esto demuestra que\(\{e_1,\: e_2,\: e_3\}\) es ortonormal.

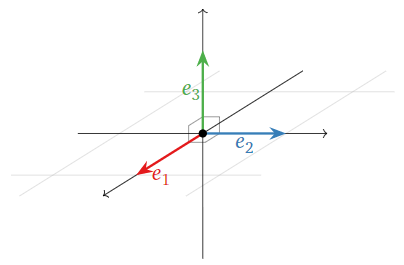
Figura\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

¿Este conjunto es ortogonal? ¿Es ortonormal?

\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\left(\begin{array}{c}1\\-2\\1\end{array}\right),\left(\begin{array}{c}1\\0\\-1\end{array}\right)\right\}\nonumber\]

Solución

Comprobamos que

\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\-2\\1\end{array}\right)=0\quad\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\-1\end{array}\right)=0\quad\left(\begin{array}{c}1\\-2\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\0\\-1\end{array}\right)=0.\nonumber\]

Por lo tanto,\(\mathcal{B}\) es ortogonal.

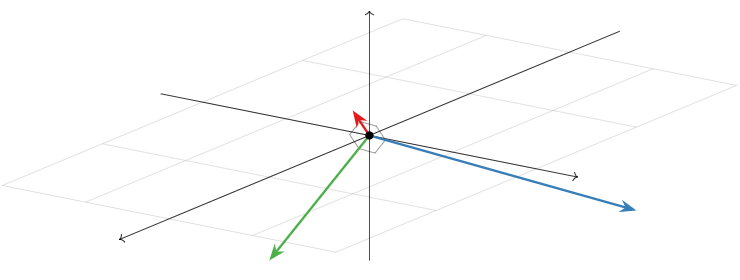
Figura\(\PageIndex{2}\)

El conjunto no\(\mathcal{B}\) es ortonormal porque, por ejemplo,

\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\1\\1\end{array}\right)=3\neq 1.\nonumber\]

Sin embargo, podemos hacerlo ortonormal reemplazando cada vector por el vector unitario en la dirección de, Fact 6.1.3 en la Sección 6.1, cada vector:

\[\left\{\frac{1}{\sqrt{3}}\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\frac{1}{\sqrt{6}}\left(\begin{array}{c}1\\-2\\1\end{array}\right),\:\frac{1}{\sqrt{2}}\left(\begin{array}{c}1\\0\\-1\end{array}\right)\right\}\nonumber\]

es ortonormal.

Vimos en el ejemplo anterior que es fácil producir un conjunto ortonormal de vectores a partir de uno ortogonal reemplazando cada vector con el vector unitario en la misma dirección.

Receta: Un conjunto ortonormal a partir de un conjunto ortogonal

Si\(\{v_1,\: v_2,\cdots ,v_m\}\) es un conjunto ortogonal de vectores, entonces

\[\left\{\frac{v_1}{||v_1||},\:\frac{v_2}{||v_2||},\cdots ,\frac{v_m}{||v_m||}\right\}\nonumber\]

es un conjunto ortonormal.

Ejemplo\(\PageIndex{3}\)

\(a,\:b\)Dejen ser escalares, y dejar

\[u_1=\left(\begin{array}{c}a\\b\end{array}\right)\quad u_2=\left(\begin{array}{c}-b\\a\end{array}\right).\nonumber\]

¿Es\(\mathcal{B}=\{u_1,\: u_2\}\) ortogonal?

Solución

Solo tenemos que verificar eso

\[\left(\begin{array}{c}a\\b\end{array}\right)\cdot\left(\begin{array}{c}-b\\a\end{array}\right)=-ab+ab=0.\nonumber\]

Por lo tanto,\(\{u_1,\:u_2\}\) es ortogonal, salvo que\(a=b=0\).

Ejemplo\(\PageIndex{4}\): Non-Example

¿Este conjunto es ortogonal?

\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\1\\1\end{array}\right),\:\left(\begin{array}{c}1\\-2\\1\end{array}\right),\:\left(\begin{array}{c}1\\-1\\-1\end{array}\right)\right\}\nonumber\]

Solución

Este conjunto no es ortogonal porque

\[\left(\begin{array}{c}1\\1\\1\end{array}\right)\cdot\left(\begin{array}{c}1\\-1\\-1\end{array}\right)=1-1-1=-1\neq 0.\nonumber\]

Veremos cómo elaborar un conjunto ortogonal a partir de\(\mathcal{B}\) en la subsección: El Proceso Gram-Schmidt.

Una propiedad agradable que disfrutan los conjuntos ortogonales es que son automáticamente linealmente independientes.

Hecho \(\PageIndex{1}\)

Un conjunto ortogonal es linealmente independiente. Por lo tanto, es una base para su lapso.

Prueba

Supongamos que\(\{u_1,\: u_2,\cdots ,u_m\}\) es ortogonal. Tenemos que demostrar que la ecuación

\[c_1u_1+c_2u_2+\cdots +c_mu_m=0\nonumber\]

tiene sólo la solución trivial\(c_1=c_2=\cdots =c_m=0\). Tomando el producto punto de ambos lados de esta ecuación con u1 da

\[\begin{aligned} 0=u_1\cdot 0&=u_1\cdot(c_1u_1+c_2u_2+\cdots +c_mu_m) \\ &=c_1(u_1\cdot u_1)+c_2(u_1\cdot u_2)+\cdots +c_m(u_1\cdot u_m) \\ &=c_1(u_1\cdot u_1)\end{aligned}\]

porque\(u_1\cdot u_i=0\) para\(i>1\). Ya\(u\neq 0\) que tenemos\(u_1\cdot u_1\neq 0\), así\(c_1=0\). De igual manera, tomar el producto punto con\(u_i\) muestra que cada uno\(c_i=0\), según se desee.

Una ventaja de trabajar con conjuntos ortogonales es que da una fórmula simple para la proyección ortogonal, Definición 6.3.2 en la Sección 6.3, de un vector.

Teorema \(\PageIndex{1}\): Projection Formula

Dejar\(W\) ser un subespacio de\(\mathbb{R}^n\), y dejar\(\{u_1,\:u_2,\cdots ,u_m\}\) ser una base ortogonal para\(W\). Entonces, para cualquier vector\(x\) en\(\mathbb{R}^n\), la proyección ortogonal de\(x\) onto\(W\) viene dada por la fórmula

\[x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]

Prueba

Let

\[y=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]

Este vector está contenido en\(W\) porque es una combinación lineal de\(u_1,\: u_2,\cdots ,u_m\). De ahí que solo necesitamos demostrar que\(x−y\) está adentro\(W^{\perp}\), es decir, eso\(u_i\cdot (x−y)=0\) para cada uno\(i=1,\: 2,\cdots ,m\). Para\(u_1\), tenemos

\[\begin{aligned}u_1\cdot (x-y)&=u_1\cdot\left(x-\frac{x\cdot u_1}{u_1\cdot u_1}u_1-\frac{x\cdot u_2}{u_2\cdot u_2}u_2-\cdots -\frac{x\cdot u_m}{u_m\cdot u_m}u_m\right) \\ &=u_1\cdot x-\frac{x\cdot u_1}{u_1\cdot u_1}(u_1\cdot u_1)-0-\cdots -0 \\ &=0.\end{aligned}\]

Un cálculo similar muestra que\(u_i\cdot (x−y)=0\) para cada uno\(i\), así\(x−y\) está en\(W^{\perp}\), según se desee.

Si\(\{u_1,\: u_2,\cdots ,u_m\}\) es una base orto normal para\(W\), entonces los denominadores\(u_i\cdot u_i=1\) desaparecen, por lo que la fórmula de proyección se vuelve aún más simple:

\[x_{W}=(x\cdot u_1)u_1+(x\cdot u_2)u_2+\cdots +(x\cdot u_m)u_m.\nonumber\]

Ejemplo\(\PageIndex{5}\)

Supongamos que\(L=\text{Span}\{u\}\) es una línea. El conjunto\(\{u\}\) es una base ortogonal para\(L\), por lo que la Fórmula de Proyección dice que para cualquier vector\(x\), tenemos

\[x_{L}=\frac{x\cdot u}{u\cdot u}u,\nonumber\]

como en el Ejemplo 6.3.7 de la Sección 6.3. Véase también el Ejemplo 6.3.8 en la Sección 6.3 y el Ejemplo 6.3.9 en la Sección 6.3.

Supongamos que\(\{u_1,\: u_2,\cdots ,u_m\}\) es una base ortogonal para un subespacio\(W\), y vamos\(L_i=\text{Span}\{u_i\}\) para cada uno\(i=1,\: 2,\cdots ,m\). Entonces vemos que para cualquier vector x, tenemos

\[\begin{aligned}x_{W}&=\frac{x\cdot u_1}{u_1\cdot u_1}u_2+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m \\ &=x_{L_{1}}+x_{L_{2}}+\cdots+x_{L_{m}}\end{aligned}\]

En otras palabras, para una base ortogonal, la\(x\) proyección de\(W\) on es la suma de las proyecciones sobre las líneas abarcadas por los vectores base. En este sentido, la proyección sobre una línea es el ejemplo más importante de una proyección ortogonal.

Ejemplo\(\PageIndex{6}\): Projection onto the \(xy\)-Plane

Continuando con el Ejemplo 6.3.1 en la Sección 6.3 y el Ejemplo 6.3.10 en la Sección 6.3, utilice la fórmula de proyección, Teorema\(\PageIndex{1}\) para calcular la proyección ortogonal de un vector sobre el\(xy\) plano en\(\mathbb{R}^{3}\).

Solución

Una base para el\(xy\) plano está dada por los dos vectores de coordenadas estándar

\[e_1=\left(\begin{array}{c}1\\0\\0\end{array}\right)\quad e_2=\left(\begin{array}{c}0\\1\\0\end{array}\right).\nonumber\]

El conjunto\(\{e_1,\:e_2\}\) es ortogonal, así que para cualquier vector\(x=(x_1,\:x_2,\:x_3)\), tenemos

\[x_{W}=\frac{x\cdot e_1}{e_1\cdot e_1}e_1+\frac{x\cdot e_2}{e_2\cdot e_2}e_2=x_1e_1+x_2e_2=\left(\begin{array}{c}x_1\\x_2\\0\end{array}\right).\nonumber\]

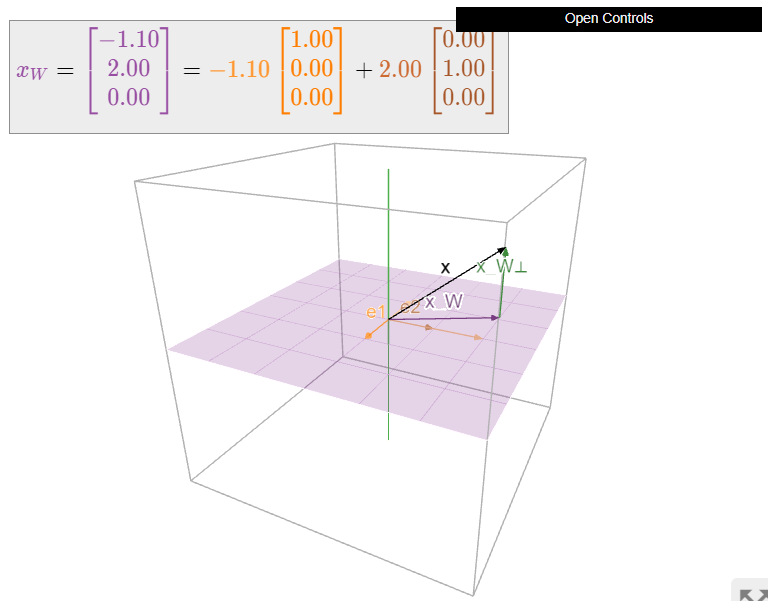
Figura\(\PageIndex{3}\): Proyección ortogonal de un vector sobre el\(xy\) plano en\(\mathbb{R}^3\). Obsérvese que\(x_{W}\) es la suma de las proyecciones de\(x\) sobre los ejes\(e_1\) - y\(e_2\) -coordenadas (mostrados en naranja y marrón, respectivamente).

Ejemplo\(\PageIndex{7}\): Projection onto a Plane in \(\mathbb{R}^3\)

Let

\[W=\text{Span}\left\{\left(\begin{array}{c}1\\0\\-1\end{array}\right),\left(\begin{array}{c}1\\1\\1\end{array}\right)\right\}\quad x=\left(\begin{array}{c}2\\3\\-2\end{array}\right).\nonumber\]

Encontrar\(x_{W}\) y\(x_{W^{\perp}}\).

Solución

Los vectores

\[u_1=\left(\begin{array}{c}1\\0\\-1\end{array}\right)\quad u_2=\left(\begin{array}{c}1\\1\\1\end{array}\right)\nonumber\]

son ortogonales, por lo que podemos usar la Fórmula de Proyección:

\[x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2=\frac{4}{2}\left(\begin{array}{c}1\\0\\-1\end{array}\right)+\frac{3}{3}\left(\begin{array}{c}1\\1\\1\end{array}\right)=\left(\begin{array}{c}3\\1\\-1\end{array}\right).\nonumber\]

Entonces tenemos

\[x_{W^{\perp}}=x-x_{W}=\left(\begin{array}{c}-1\\2\\-1\end{array}\right).\nonumber\]

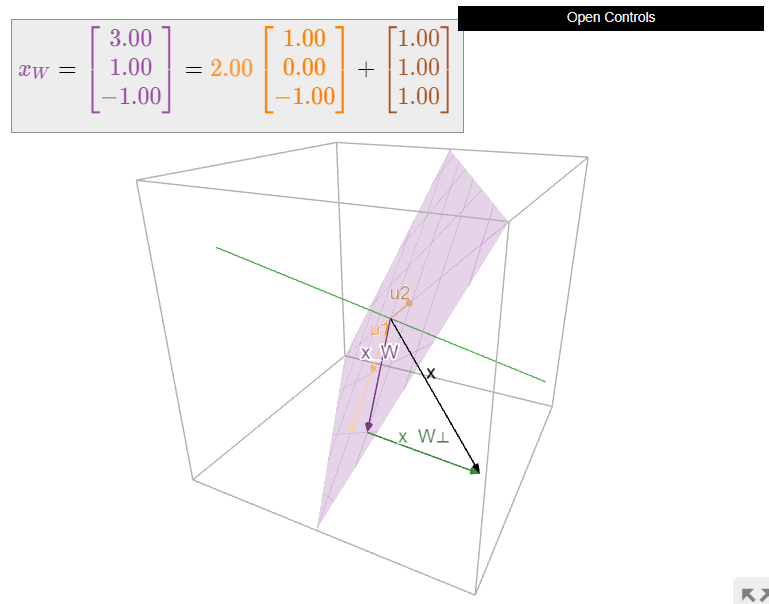
Figura\(\PageIndex{4}\): Proyección ortogonal de un vector sobre el plano\(W\). Obsérvese que\(x_W\) es la suma de las proyecciones de\(x\) sobre las líneas\(u_1\) abarcadas por y\(u_2\) (mostradas en naranja y marrón, respectivamente).

Ejemplo\(\PageIndex{8}\): Projection onto a 3-Space in \(\mathbb{R}^4\)

Let

\[W=\text{Span}\left\{\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right),\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right),\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\right\}\quad x=\left(\begin{array}{c}0\\1\\3\\4\end{array}\right).\nonumber\]

Calcular\(x_{W}\), y encontrar la distancia de\(x\) a\(W\).

Solución

Los vectores

\[u_1=\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right)\quad u_2=\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right)\quad u_3=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\nonumber\]

son ortogonales, por lo que podemos usar la Fórmula de Proyección:

\[\begin{aligned} x_{W}&=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\frac{x\dot u_3}{u_3\cdot u_3}u_3 \\ &=\frac{-3}{2}\left(\begin{array}{c}1\\0\\-1\\0\end{array}\right)+\frac{-3}{2}\left(\begin{array}{c}0\\1\\0\\-1\end{array}\right)+\frac{8}{4}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)=\frac{1}{2}\left(\begin{array}{c}1\\1\\7\\7\end{array}\right) \\ x_{W^{\perp}}&=x-x_{W}=\frac{1}{2}\left(\begin{array}{c}-1\\1\\-1\\1\end{array}\right).\end{aligned}\]

La distancia de\(x\) a\(W\) es

\[||x_{W^{\perp}}||=\frac{1}{2}\sqrt{1+1+1+1}=1.\nonumber\]

Ahora deja\(W\) ser un subespacio de\(\mathbb{R}^n\) con base ortogonal\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\), y deja\(x\) ser un vector adentro\(W\). Entonces\(x=x_{W}\), así por la fórmula de proyección, Teorema\(\PageIndex{1}\), tenemos

\[x=x_{W}=\frac{x\cdot u_1}{u_1\cdot u_1}u_1+\frac{x\cdot u_2}{u_2\cdot u_2}u_2+\cdots +\frac{x\cdot u_m}{u_m\cdot u_m}u_m.\nonumber\]

Esto nos da una manera de expresar\(x\) como una combinación lineal de los vectores base en\(\mathcal{B}\): hemos calculado las\(\mathcal{B}\) -coordenadas, Definición 2.8.1 en la Sección 2.8, ¡de\(x\) sin reducción de filas!

Receta:\(\mathcal{B}\)-Coordinates when \(\mathcal{B}\) is an Orthogonal Set

Dejar\(W\) ser un subespacio de\(\mathbb{R}^n\) con base ortogonal\(\mathcal{B}=\{v_1,\: v_2,\cdots ,v_m\}\) y dejar\(x\) ser un vector en\(W\). Entonces

\[[x]_{\mathcal{B}}=\left(\frac{x\cdot u_1}{u_1\cdot u_1},\:\frac{x\cdot u_2}{u_2\cdot u_2},\cdots ,\frac{x\cdot u_m}{u_m\cdot u_m}\right).\nonumber\]

Al igual que con las proyecciones ortogonales, si\(\{u_1,\: u_2,\cdots ,u_m\}\) es una base orto normal de\(W\), entonces la fórmula es aún más simple:

\[[x]_{\mathcal{B}}=\left(x\cdot u_1,\: x\cdot u_2,\cdots ,x\cdot u_m\right).\nonumber\]

Ejemplo\(\PageIndex{9}\): Computing Coordinates with Respect to an Orthogonal Basis

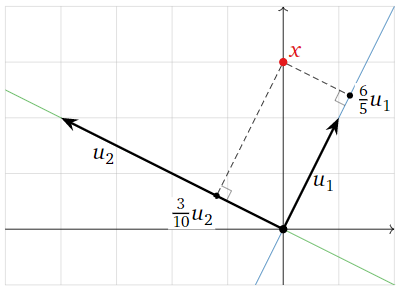
Encuentra las\(\mathcal{B}\) coordenadas de\(x\), donde

\[\mathcal{B}=\left\{\left(\begin{array}{c}1\\2\end{array}\right),\left(\begin{array}{c}-4\\2\end{array}\right)\right\}\quad x=\left(\begin{array}{c}0\\3\end{array}\right).\nonumber\]

Solución

Desde

\[u_1=\left(\begin{array}{c}1\\2\end{array}\right)\quad u_2=\left(\begin{array}{c}-4\\2\end{array}\right)\nonumber\]

formar una base ortogonal de\(\mathbb{R}^2\), tenemos

\[[x]_{\mathcal{B}}=\left(\frac{x\cdot u_1}{u_1\cdot u_1},\frac{x\cdot u_2}{u_2\cdot u_2}\right)=\left(\frac{3\cdot 2}{1^2+2^2},\frac{3\cdot 2}{(-4)^2+2^2}\right)=\left(\frac{6}{5},\frac{3}{10}\right).\nonumber\]

Figura\(\PageIndex{5}\)

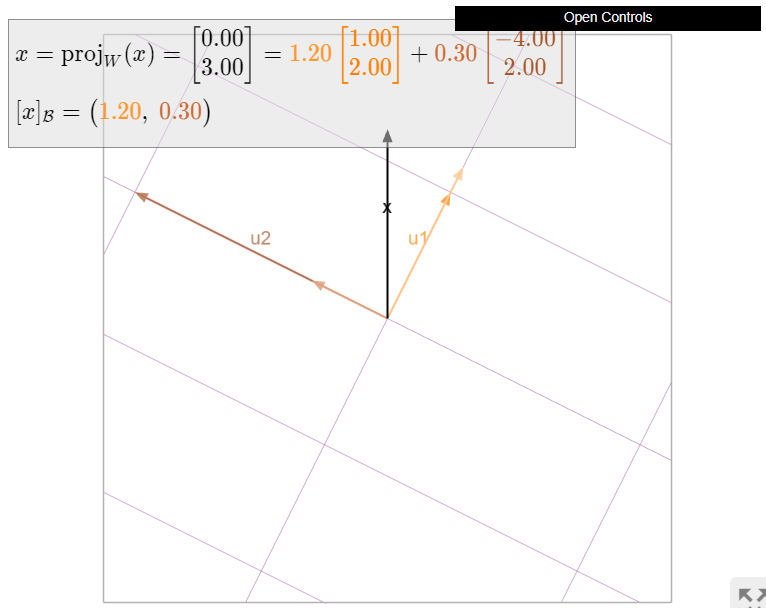
Figura\(\PageIndex{6}\): Computación\(\mathcal{B}\) de coordenadas usando la Fórmula de Proyección.

El siguiente ejemplo muestra que la Fórmula de Proyección de hecho requiere una base ortogonal.

Ejemplo\(\PageIndex{10}\): Non-Example: A Non-Orthogonal Basis

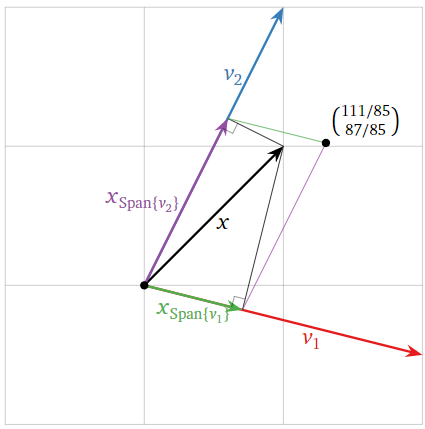
Considerar la base\(\mathcal{B}=\{v_1,\: v_2\}\) de\(\mathbb{R}^2\), donde

\[v_1=\left(\begin{array}{c}2\\-1/2\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\2\end{array}\right).\nonumber\]

Esto no es ortogonal porque\(v_1\cdot v_2=2−1=1\neq 0\). Vamos\(x=\left(\begin{array}{c}1\\1\end{array}\right)\). Intentemos calcular\(x=x_{\mathbb{R}^{2}}\) usando la Fórmula de Proyección con respecto a la base\(\mathcal{B}\):

\[x_{\mathbb{R}^{2}}=\color{Green}{\frac{x\cdot v_1}{v_1\cdot v_1}v_1}\color{black}{+}\color{Purple}{\frac{x\cdot v_2}{v_2\cdot v_2}v_2}\color{black}{=}\color{Green}{\frac{3/2}{17/4}\left(\begin{array}{c}2\\-1/2\end{array}\right)}\color{black}{+}\color{Purple}{\frac{3}{5}\left(\begin{array}{c}1\\2\end{array}\right)}\color{black}{=\left(\begin{array}{c}111/85\\ 87/85\end{array}\right)\neq x.}\nonumber\]

Ya que\(x=x_{\mathbb{R}^{2}}\), vemos que la Fórmula de Proyección no calcula la proyección ortogonal en este caso. Geométricamente, las proyecciones de\(x\) sobre las líneas abarcadas por\(v_1\) y\(v_2\) no se suman a\(x\), como podemos ver en la imagen.

Figura\(\PageIndex{7}\)

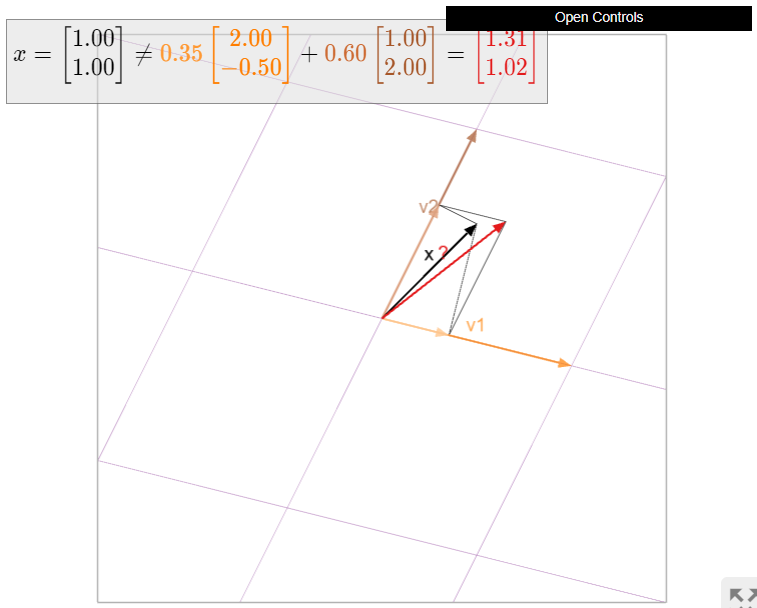
Figura\(\PageIndex{8}\): Cuando\(v_1\) y no\(v_2\) son ortogonales, entonces no\(x_{\mathbb{R}^{2}}=x\) es necesariamente igual a la suma (rojo) de las proyecciones (naranja y marrón) de\(x\) sobre las líneas abarcadas por\(v_1\) y\(v_2\).

Nota\(\PageIndex{1}\)

Se necesita una base ortogonal para usar la Fórmula de Proyección.

El proceso Gram-Schmidt

Vimos en la subsección anterior que las proyecciones ortogonales y las\(\mathcal{B}\) coordenadas son mucho más fáciles de calcular en presencia de una base ortogonal para un subespacio. En esta subsección, damos un método, llamado Proceso Gram—Schmidt, para computar una base ortogonal de un subespacio.

Teorema\(\PageIndex{2}\): The Gram-Schmidt Process

Dejar\(v_1,\: v_2,\cdots ,v_m\) ser una base para un subespacio\(W\) de\(\mathbb{R}^{n}\). Definir:

1. \(u_1=v_1\)
2. \(u_2=(v_2)_{\text{Span}\{u_1\}^{\perp}}\qquad\qquad =v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1\)
3. \(u_3=(v_3)_{\text{Span}\{u_1,u_2\}^{\perp}}\qquad\quad\; =v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2\)

\(\quad\vdots\)

13. \(u_m=(v_m)_{\text{Span}\{u_1,u_2,\cdots ,u_{m-1}\}^{\perp}}=v_m-\sum\limits_{i=1}^{m-1}\frac{v_m\cdot u_i}{u_i\cdot u_i}u_i\).

Entonces\(\{u_1,\: u_2,\cdots ,u_m\}\) es una base ortogonal para el mismo subespacio\(W\).

Prueba

Primero afirmamos que cada uno\(u_i\) está adentro\(W\), y de hecho eso\(u_i\) está adentro\(\text{Span}\{v_1,\: v_2,\cdots ,v_i\}\). Claramente\(u_1=v_1\) está en\(\text{Span}\{v_1\}\). Entonces\(u_2\) es una combinación lineal de\(u_1\) y\(v_2\), que están ambos en\(\text{Span}\{v_1,\: v_2\}\), así\(u_2\) es en\(\text{Span}\{v_1,\:v_2\}\) también. Del mismo modo,\(u_3\) es una combinación lineal de\(u_1,\: u_2\), y\(v_3\), que están todos adentro\(\text{Span}\{v_1,\: v_2,\: v_3\}\), así\(u_3\) es en\(\text{Span}\{v_1,\: v_2,\: v_3\}\). Continuando de esta manera, vemos que cada uno\(u_i\) está adentro\(\text{Span}\{v_1,\: v_2,\cdots ,v_i\}\).

Ahora afirmamos que\(\{u_1,\: u_2,\cdots ,u_m\}\) es un conjunto ortogonal. Vamos\(1\leq i < j\leq m\). Entonces\(u_j=(v_j)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{j−1}\}^{\perp}}\), por definición\(u_j\) es ortogonal a cada vector en\(\text{Span}\{u_1,\:u_2,\cdots ,u_{j−1}\}\). En particular,\(u_j\) es ortogonal a\(u_i\).

Todavía tenemos que demostrar que cada uno\(u_i\) es distinto de cero. Claramente\(u_1=v_1\neq 0\). Supongamos que\(u_i=0\). Entonces\((v_i)_{\text{Span}\{u_1,\:u_2,\cdots,u_{i−1}\}^{\perp}}=0\), lo que significa que\(v_i\) está adentro\(\text{Span}\{u_1,\:u_2,\cdots ,u_{i−1}\}\). Pero cada uno\(u_1,\: u_2,\cdots ,u_{i−1}\) está en\(\text{Span}\{v_1,\:v_2,\cdots ,v_{i−1}\}\) por el primer párrafo, así\(v_i\) está en\(\text{Span}\{v_1,\: v_2,\cdots ,v_{i−1}\}\). Esto contradice el criterio de lapso creciente Teorema 2.5.2 en la Sección 2.5; por lo tanto,\(u_i\) debe ser distinto de cero.

Los dos párrafos anteriores justifican el uso de la fórmula de proyección, Teorema\(\PageIndex{1}\), en las igualdades

\[(v_i)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{i-1}\}^{\perp}}=v_i-(v_i)_{\text{Span}\{u_1,\:u_2,\cdots ,u_{i-1}\}}=v_i-\sum\limits_{j=1}^{i-1}\frac{v_i\cdot u_j}{u_j\cdot u_j}u_j\nonumber\]

en el enunciado del teorema.

Dado que\(\{u_1,\: u_2,\cdots ,u_m\}\) es un conjunto ortogonal, es linealmente independiente. Así se trata de un conjunto de vectores\(m\) linealmente independientes en\(W\), por lo que es una base para\(W\) por el teorema de base, Teorema 2.7.3 en la Sección 2.7. Del mismo modo, para cada\(i\), vimos que el conjunto\(\{u_1,\: u_2,\cdots ,u_i\}\) está contenido en el subespacio\(i\) -dimensional\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\), por lo que\(\{u_1,\:u_2,\cdots ,u_i\}\) es una base ortogonal para\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\).

Ejemplo\(\PageIndex{11}\): Two Vectors

Encontrar una base ortogonal\(\{u_1,\:u_2\}\) para\(W=\text{Span}\{v_1,\:v_2\}\), donde

\[v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\1\\1\end{array}\right).\nonumber\]

Solución

Ejecutamos Gram—Schmidt: primero toma\(u_1=v_1\), luego

\[u_2=v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}1\\1\\1\end{array}\right)-\frac{2}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right).\nonumber\]

Entonces\(\{u_1,\:u_2\}\) es una base ortogonal para\(W\): en efecto, es claro que\(u_1\cdot u_2=0\).

Geométricamente, simplemente estamos reemplazando\(v_2\) con la parte de\(v_2\) que es perpendicular a la línea\(L_1=\text{Span}\{v_1\}\):

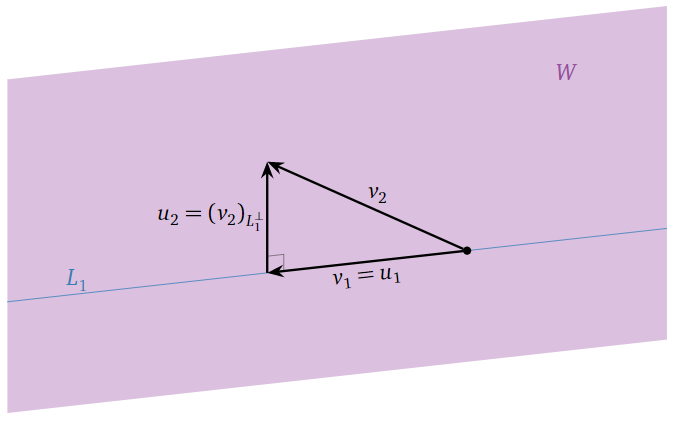
Figura\(\PageIndex{9}\)

Ejemplo\(\PageIndex{12}\): Three Vectors

Encontrar una base ortogonal\(\{u_1,\: u_2,\:u_3\}\) para\(W=\text{Span}\{v_1,\:v_2,\:v_3\}=\mathbb{R}^3\), donde

\[v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\quad v_2=\left(\begin{array}{c}1\\1\\1\end{array}\right)\quad v_3=\left(\begin{array}{c}3\\1\\1\end{array}\right).\nonumber\]

Solución

Ejecutamos Gram-Schmidt:

1. \(u_1=v_1=\left(\begin{array}{c}1\\1\\0\end{array}\right)\)
2. \(u_2=v_2=\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}1\\1\\1\end{array}\right)-\frac{2}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)=\left(\begin{array}{c}0\\0\\1\end{array}\right)\)
3. \(\begin{aligned}u_3&=v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2 \\ &=\left(\begin{array}{c}3\\1\\1\end{array}\right)-\frac{4}{2}\left(\begin{array}{c}1\\1\\0\end{array}\right)-\frac{1}{1}\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{c}1\\-1\\0\end{array}\right).\end{aligned}\)

Entonces\(\{u_1,\:u_2,\:u_3\}\) es una base ortogonal para\(W\): en efecto, tenemos

\[u_1\cdot u_2=0\quad u_1\cdot u_3=0\quad u_2\cdot u_3=0.\nonumber\]

Geométricamente, una vez que tenemos\(u_1\) y\(u_2\), reemplazamos\(v_3\) por la parte que es ortogonal a\(W_2=\text{Span}\{u_1,\:u_2\}=\text{Span}\{v_1,\:v_2\}\):

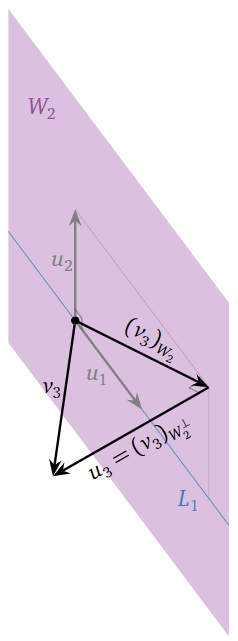
Figura\(\PageIndex{10}\)

Ejemplo\(\PageIndex{13}\): Three Vectors in \(\mathbb{R}^4\)

Encontrar una base ortogonal\(\{u_1,\:u_2,\:u_3\}\) para\(W=\text{Span}\{v_1,\:v_2,\:v_3\}\), donde

\[v_1=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\quad v_2=\left(\begin{array}{c}-1\\4\\4\\-1\end{array}\right)\quad v_3=\left(\begin{array}{c}4\\-2\\-2\\0\end{array}\right).\nonumber\]

Solución

Ejecutamos Gram—Schmidt:

1. \(u_1=v_1=\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)\)
2. \(u_2=v_2-\frac{v_2\cdot u_1}{u_1\cdot u_1}u_1=\left(\begin{array}{c}-1\\4\\4\\-1\end{array}\right)-\frac{6}{4}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)=\left(\begin{array}{c}-5/2\\5/2\\5/2\\-5/2\end{array}\right)\)
3. \(\begin{aligned}u_3&=v_3-\frac{v_3\cdot u_1}{u_1\cdot u_1}u_1-\frac{v_3\cdot u_2}{u_2\cdot u_2}u_2 \\ &=\left(\begin{array}{c}4\\-2\\-2\\0\end{array}\right)-\frac{0}{24}\left(\begin{array}{c}1\\1\\1\\1\end{array}\right)-\frac{-20}{25}\left(\begin{array}{c}-5/2\\5/2\\5/2\\-5/2\end{array}\right)=\left(\begin{array}{c}2\\0\\0\\-2\end{array}\right).\end{aligned}\)

Entonces\(\{u_1,\:u_2,\:u_3\}\) es una base ortogonal para\(W\).

Vimos en la prueba del Proceso Gram—Schmidt que para cada\(i\) entre\(1\) y\(m\), el conjunto\(\{u_1,\:u_2,\cdots ,u_i\}\) es una base ortogonal para\(\text{Span}\{v_1,\:v_2,\cdots ,v_i\}\).

Si hubiéramos comenzado con un conjunto de expansión\(\{v_1,\:v_2,\cdots ,v_m\}\) que es linealmente dependiente, entonces para algunos\(i\), el vector\(v_i\) está adentro\(\text{Span}\{v_1,\:v_2,\cdots ,v_{i−1}\}\) por el criterio de span creciente, Teorema 2.5.2 en la Sección 2.5. De ahí

\[0=(v_i)_{\text{Span}\{v_1,\:v_2,\cdots ,v_{i-1}\}^{\perp}}=(v_i)_{\text{Span}\{u_1,\:u_2,\cdots u_{i-1}\}^{\perp}}=u_i.\nonumber\]

Nota\(\PageIndex{2}\)

Puede usar el proceso Gram—Schmidt para producir una base ortogonal a partir de cualquier conjunto de expansión: si hay alguno\(u_i=0\), simplemente deseche\(u_i\) y\(v_i\), y continúe.