9.6: Proyecciones ortogonales y problemas de minimización
- Page ID
- 115083
{{Template.dropdown {ruta:” /álgebra/linear_álgebra "}}}
Definición 9.6.1 Dejar\(V \) ser un espacio de producto interior finito-dimensional y\(U\subset V \) ser un subconjunto (pero no necesariamente un subespacio) de\(V\). Entonces el complemento ortogonal de\(U \) se define como el conjunto
\[ U^\bot = \{ v \in V \mid \inner{u}{v}=0 ~\rm{for~ all}~ u\in U \} .\]
Tenga en cuenta que, de hecho, siempre\(U^\bot \) es un subespacio de\(V \) (¡como debe comprobar!) y que
\[ \{0\}^\bot = V \quad \text{and} \quad V^\bot = \{0\}. \]
Además, si\(U_{1} \) y\(U_{2} \) son subconjuntos de\(V \) satisfactorios\(U_1\subset U_2\), entonces\(U_2^\bot \subset U_1^\bot\). Sorprendentemente, si\(U\subset V \) es un subespacio de\(V\), entonces podemos decir bastante más sobre\(U^{\bot}\).
Teorema 9.6.2. Si\(U\subset V \) es un subespacio de\(V\), entonces\(V=U\oplus U^\bot\).
Comprobante. Tenemos que mostrar dos cosas:
- \(V=U+U^\bot\).
- \(U\cap U^\bot = \{0\}\).
Para mostrar Condición~1 sostiene, dejar\((e_1,\ldots,e_m) \) ser una base ortonormal de\(U\). Entonces, para todos\(v\in V\), podemos escribir
\ begin {ecuación}\ label {eQ:u Ubot}
v=\ underbrackets {\ inner {v} {e_1} e_1 +\ cdots +\ inner {v} {e_m} e_m} _u +
\ underbrackets {v-\ inner {v} {e_1} e_1 -\ cdots -\ inner {v} {e_m} e_m} _w.\ tag {9.6.1}
\ end {ecuación}
El vector \(u\in U\), y
\ begin {ecuación*}
\ inner {w} {e_j} =\ inner {v} {e_j} -\ inner {v} {e_j} =0, ~\ rm {for~ all} ~ {j=1,2,\ ldots, m,}
\ end {ecuación*}
ya que\((e_1,\ldots,e_m) \) es una lista ortonormal de vectores. De ahí,\(w\in U^\bot\). Esto implica que\(V=U+U^\bot\).
Para probar que Condition~2 también se mantiene, vamos\(v\in U\cap U^\bot\). Entonces\(v \) tiene que ser ortogonal a cada vector en\(U\), incluso a sí mismo, y así\(\inner{v}{v}=0\). Sin embargo, esto implica\(v=0 \) así que\(U\cap U^\bot=\{0\}\).
Ejemplo 9.6.3. \(\mathbb{R}^2 \)es la suma directa de dos líneas ortogonales cualesquiera, y\(\mathbb{R}^3 \) es la suma directa de cualquier plano y cualquier línea ortogonal al plano como se ilustra en la Figura 9.6.1. Por ejemplo,
\ begin {ecuation*}
\ begin {split}
\ mathbb {R} ^2 &=\ {(x,0)\ mid x\ in\ mathbb {R}\}\ oplus\ {(0, y)\ mid y\ in\ mathbb {R}\},\
\ mathbb {R} ^3 &=\ {(x, y,0)\ mid x, y\ in\ mathbb {R}\}\ oplus\ {(0,0, z)\ mid z\ in\ mathbb {R}\}.
\ end {split}
\ end {ecuación*}
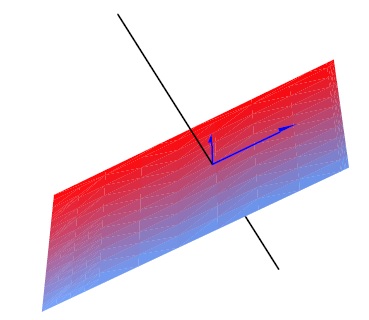
Figura 9.6.1:\( \mathbb{R^3} \) como suma directa de un plano y una línea.
Otro dato fundamental sobre el complemento ortogonal de un subespacio es el siguiente.
Teorema 9.6.4. Si\(U\subset V \) es un subespacio de\(V\), entonces\(U=(U^\bot)^\bot\).
Comprobante. Primero lo demostramos\(U\subset (U^\bot)^\bot\). Vamos\(u\in U\). Entonces, para todos\(v\in U^\bot\), tenemos\(\inner{u}{v}=0\). De ahí,\(u\in (U^\bot)^\bot \) por la definición de\((U^\bot)^\bot\).
A continuación lo demostramos\((U^\bot)^\bot\subset U\). Supongamos\(0\neq v\in (U^\bot)^\bot \) tal que\(v\not\in U\), y descomponerse\(v \) según el Teorema 9.6.2, es decir, como
\ begin {ecuación*}
v = u_1 + u_2\ in U\ oplus U^\ bot
\ end {ecuación*}
con\(u_1\in U \) y\(u_2\in U^\bot\). Entonces\(u_2\neq 0 \) desde\(v\not\in U\).
Además,\(\inner{u_2}{v} = \inner{u_2}{u_2} \neq 0\). Pero entonces no\(v \) está en\((U^\bot)^\bot\), lo que contradice nuestra suposición inicial. De ahí, debemos tener eso\((U^\bot)^\bot\subset U\).
Por Teorema 9.6.2, tenemos la descomposición\(V=U\oplus U^\bot \) para cada subespacio\(U\subset V\). Esto nos permite definir la proyección ortogonal\(P_U \) de\(V \) sobre\(U\).
Definición 9.6.5. Dejar\(U\subset V \) ser un subespacio de un espacio de producto interior finito-dimensional. Cada uno se\(v\in V \) puede escribir de manera única como\(v=u+w \) dónde\(u\in U \) y\(w\in U^\bot\). Definir
\ begin {ecuación*}
\ begin {split}
P_U:V &\ a V,\\
v &\ mapsto u.
\ end {split}
\ end {equation*}
Tenga en cuenta que\(P_U \) se llama operador de proyección ya que satisface\(P_U^2=P_U\). Además, como también tenemos
\ begin {equation*}
\ begin {split}
&\ range (P_U) = U,\\
&\ kernel (P_U) = U^\ bot,
\ end {split}
\ end {equation*}
se deduce de eso\(\range(P_U) \bot \kernel(P_U)\). Por lo tanto,\(P_U \) se denomina proyección ortogonal.
La descomposición de un vector\(v\in V\) como se da en la Ecuación (9.6.1) produce la fórmula
\ begin {ecuación}\ label {eq:orto decomp}
P_U v =\ inner {v} {e_1} e_1 +\ cdots +\ inner {v} {e_m} e_m,\ tag {9.6.2}
\ end {ecuación}
donde\((e_1,\ldots,e_m) \) está cualquier base ortonormal de \(U\). La ecuación (9.6.2) es una herramienta particularmente útil para computar cosas como la matriz de\(P_{U} \) respecto a la base\((e_1,\ldots,e_m)\).
Ahora apliquemos el producto interno al siguiente problema de minimización: Dado un subespacio\(U\subset V \) y un vector\(v\in V\), encontrar el vector\(u\in U \) que está más cerca del vector\(v\). En otras palabras, queremos hacer\(\norm{v-u} \) lo más pequeño posible. La siguiente proposición muestra que\(P_Uv \) es el punto más cercano\(U \) al vector\(v \) y que este mínimo es, de hecho, único.
Proposición 9.6.6. Que\(U\subset V \) sea un subespacio de\(V \) y\(v\in V\). Entonces
\[ \norm{v-P_Uv} \le \norm{v-u} \qquad \text{for every \(u\in U\).}\]
Además, la igualdad se mantiene si y solo si\(u=P_Uv\).
Comprobante. Dejar\(u\in U \) y establecer\(P:=P_U \) para abreviar. Entonces
\ begin {ecuación*}
\ begin {split}
\ norm {v-p v} ^2 &\ le\ norm {v-p v} ^2 +\ norm {pv-u} ^2\\
&=\ norm {(v-p v) + (P v-u)} ^2 =\ norm {v-u} ^2,
\ end {split}
\ end {ecuación*}
donde la segunda línea sigue de la Teorema de Pitágoras 9.3.2~\ ref {thm:pitágoras} desde\(v-Pv\in U^\bot \) y\(Pv-u\in U\). Además, la igualdad se mantiene sólo si\(\norm{Pv-u}^2=0\), que es equivalente a\(Pv=u\).
Ejemplo 9.6.7. Considera el plano\(U\subset \mathbb{R}^3 \) a través de 0 y perpendicular al vector\(u=(1,1,1)\). Usando la norma estándar on\(\mathbb{R}^3\), podemos calcular la distancia del punto\(v=(1,2,3) \) a\(U \) usar la Proposición 9.6.6. En particular, la distancia\(d \) entre\(v \) y\(U \) viene dada por\(d=\norm{v-P_Uv}\). Dejar\((\frac{1}{\sqrt{3}}u,u_1,u_2) \) ser una base para\(\mathbb{R}^3 \) tal que\((u_1,u_2) \) sea una base ortonormal de\(U\). Entonces, por la Ecuación (9.6.2), tenemos
\ begin {align*}
v-p_UV & = (\ frac {1} {3}\ inner {v} {u} u+\ inner {v} {u_1} u_1+\ inner {v} {u_2} u_2) - (\ inner {v} {u_1} u_1 +\ inner {v} {u_2} _2)\\
& =\ frac {1} {3}\ interior {v} {u} u\\
& =\ frac {1} {3}\ interior {(1,2,3)} {(1,1,1)} (1,1,1)\\
& = (2,2,2).
\ end {align*}
Por lo tanto,\(d=\norm{(2,2,2)}=2\sqrt{3}\).


