4.1: Mínimos Cuadrados
- Page ID
- 113154
Introducción
Aprendimos en el capítulo anterior que no es\(Ax = b\) necesario poseer una solución cuando el número de filas de\(A\) excede su rango, es decir,\(r < m\). Como esta situación surge con bastante frecuencia en la práctica, típicamente bajo la apariencia de 'más ecuaciones que incógnitas', establecemos una justificación para lo absurdo\(Ax = b\).
Las ecuaciones normales
El objetivo es elegir\(x\) tal que\(Ax\) esté lo más cerca posible de\(b\). Midiendo la cercanía en términos de la suma de los cuadrados de los componentes llegamos al problema de 'mínimos cuadrados' de minimizar
res
\[(||Ax-b||)^2 = (Ax-b)^{T}(Ax-b) \nonumber\]
sobre todo\(x \in \mathbb{R}\). El camino hacia la solución es iluminado por el Teorema Fundamental. Más precisamente, escribimos
\(\forall b_{R}, b_{N}, b_{R} \in \mathbb{R}(A) \wedge b_{N} \in \mathbb{N} (A^{T}) : (b = b_{R}+b_{N})\). Al señalar que (i)\(\forall b_{R}, x \in \mathbb{R}^n : ((Ax-bR) \in \mathbb{R}(A))\) y (ii)\(\mathbb{R}(A) \perp \mathbb{N} (A^T)\) llegamos al Teorema de Pitágoras.
\[norm^{2}(Ax-b) = (||Ax-b_{R}+b_{N}||)^2 \nonumber\]
\[= (||Ax-b_{R}||)^2+(||b_{N}||)^2 \nonumber\]
Ahora queda claro del Teorema de Pitágoras que el mejor\(x\) es el que satisface
\[Ax = b_{R} \nonumber\]
Como\(b_{R} \in \mathbb{R}(A)\) esta ecuación en efecto posee una solución. Sin embargo, todavía tenemos que especificar cómo se calcula\(b_{R}\) dado\(b\). Si bien una expresión explícita para la proyección\(b_{R}\) ortogonal de\(b\) sobre\(\mathbb{R}(A)\), en términos de\(A\) y\(b\) está a nuestro alcance, estrictamente hablando, no la requeriremos. Para ver esto, notemos que si\(x\) satisface la ecuación anterior entonces la proyección ortogonal de\(b\) sobre\(\mathbb{R}(A)\), en términos de\(A\) y\(b\) está a nuestro alcance, estrictamente hablando, no la requeriremos. Para ver esto, notemos que si\(x\) satisface la ecuación anterior entonces
\[Ax-b = Ax-b_{R}+b_{N} \nonumber\]
\[= -b_{N} \nonumber\]
Como no\(b_{N}\) se calcula más fácilmente de\(b_{R}\) lo que puede afirmar que sólo vamos en círculos. Sin embargo, la información 'práctica' en la ecuación anterior es que\((Ax-b) \in A^{T}\), es decir\(A^{T}(Ax-b) = 0\), es decir,
\[A^{T} Ax = A^{T} b \nonumber\]
Como\(A^{T} b \in \mathbb{R} (A^T)\) independientemente de\(b\) este sistema, a menudo referido como las ecuaciones normales, de hecho tiene una solución. Esta solución es única siempre y cuando las columnas de\(A^{T}A\) sean linealmente independientes, es decir, siempre y cuando\(\mathbb{N}(A^{T}A) = {0}\). Recordando el Capítulo 2, Ejercicio 2, observamos que esto equivale a\(\mathbb{N}(A) = \{0\}\)
El conjunto de\(x \in b_{R}\) para el que el inadaptado\((||Ax-b||)^2\) es más pequeño está compuesto por aquellos\(x\) para los que Siempre\(A^{T}Ax = A^{T}b\) hay al menos uno de esos\(x\). Hay exactamente uno de esos\(x\) si\(\mathbb{N}(A) = \{0\}\).
Como ejemplo concreto, supongamos con referencia a la Figura 1 que\(A = \begin{pmatrix} {1}&{1}\\ {0}&{1}\\ {0}&{0} \end{pmatrix}\) y\(A = \begin{pmatrix} {1}\\ {1}\\ {1} \end{pmatrix}\)
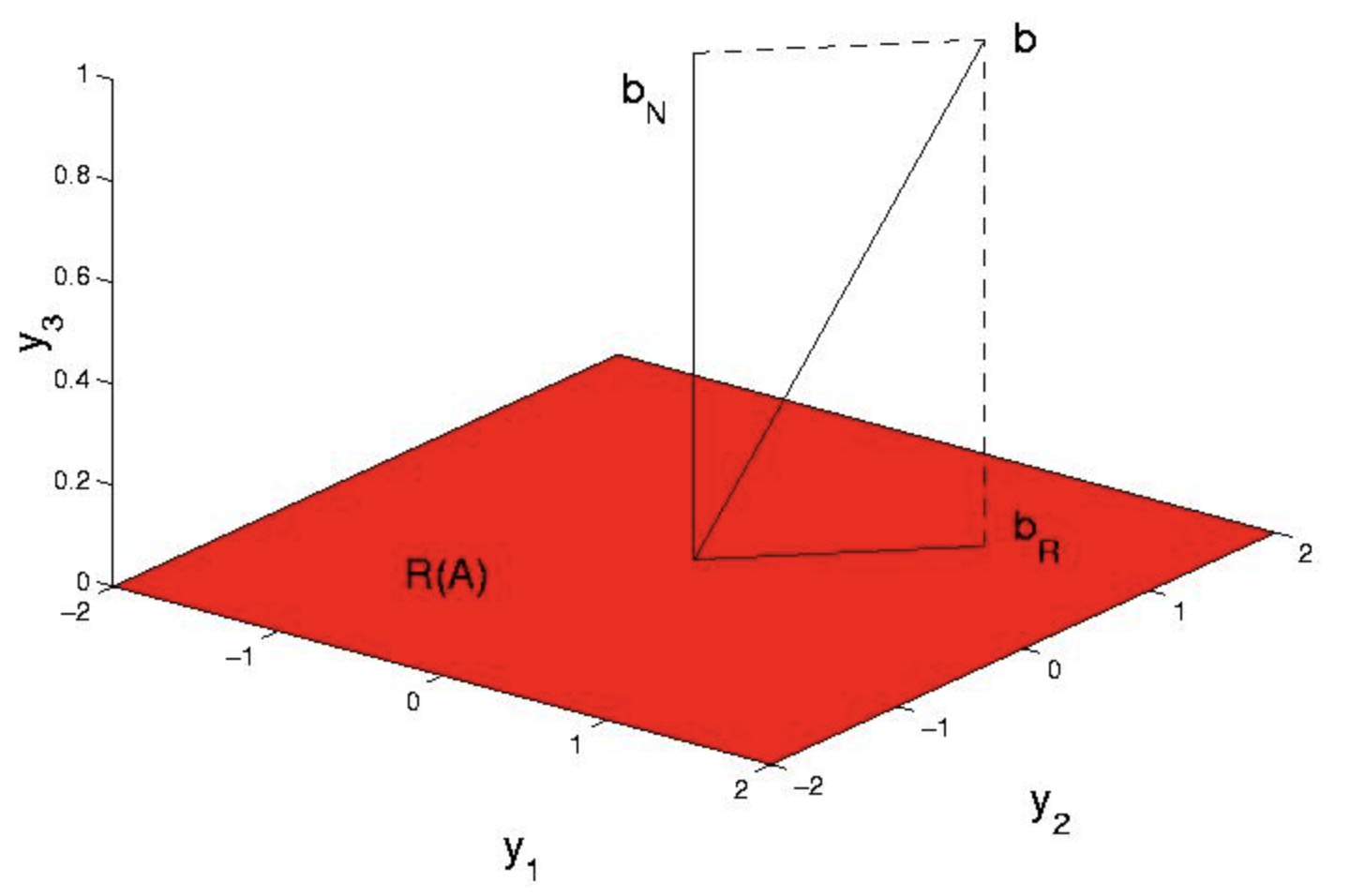
Como no\(b \ne \mathbb{R}(A)\) hay\(x\) tal que\(Ax = b\). En efecto\((||Ax-b||)^2 = (x_{1}+x_{2}+-1)^2+(x_{2}-1)^2+1 \ge 1\),, con el mínimo obtenido de manera única en\(x = \begin{pmatrix} {0}\\ {1} \end{pmatrix}\), de acuerdo con la solución única de la ecuación anterior, para\(A^{T} A = \begin{pmatrix} {1}&{1}\\ {1}&{2} \end{pmatrix}\) y\(A^{T} b = \begin{pmatrix} {1}\\ {2} \end{pmatrix}\). Ahora reconocemos, a posteriori, que\(b_{R} = Ax = \begin{pmatrix} {1}\\ {1}\\ {0} \end{pmatrix}\) es la proyección ortogonal de b sobre el espacio de columna de\(A\).
Aplicación de mínimos cuadrados al problema de la prueba biaxial
Formularemos la identificación de las 20 rigideces de fibra en esta figura anterior, como problema de mínimos cuadrados. Visualizamos la carga, los 9 nodos y midiendo los 18 desplazamientos asociados,\(x\). A partir del conocimiento\(x\) y\(f\) deseamos inferir los componentes de\(K=diag(k)\) donde\(k\) se encuentra el vector de rigideces de fibra desconocidas. El primer paso es reconocer que
\[A^{T}KAx = f \nonumber\]
puede escribirse como
\[\forall B, B = A^{T} diag(Ax) : (Bk = f) \nonumber\]
Aunque conceptualmente simple esto no es de gran utilidad en la práctica, pues\(B\) es de 18 por 20 y de ahí que la ecuación anterior posee muchas soluciones. La salida es computar\(k\) como resultado de más de un experimento. Veremos que, para nuestra pequeña muestra, bastarán 2 experimentos. Para ser precisos, suponemos que\(x^1\) es el desplazamiento producido por la carga\(f^1\) mientras que\(x^2\) es el desplazamiento producido por la carga\(f^2\). Luego recogimos las piezas asociadas en
\[B = \begin{pmatrix} {A^{T} \text{diag} (Ax^1)}\\ {A^{T} \text{diag} (Ax^2)} \end{pmatrix}\]
y
\[f= \begin{pmatrix} {f^1}\\ {f^2} \end{pmatrix}.\]
Esto\(B\) es 36-por-20 y así el sistema\(Bk = f\) está sobredeterminado y por lo tanto maduro para mínimos cuadrados.
Se procede entonces a ensamblar\(B\) y\(f\). Suponemos\(f^{1}\) y\(f^{2}\) para corresponder al estiramiento horizontal y vertical
\[f^{1} = \begin{pmatrix} {-1}&{0}&{0}&{0}&{1}&{0}&{-1}&{0}&{0}&{0}&{1}&{0}&{-1}&{0}&{0}&{0}&{1}&{0} \end{pmatrix}^{T} \nonumber\]
\[f^{2} = \begin{pmatrix} {0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{1}&{0}&{-1}&{0}&{-1}&{0}&{-1} \end{pmatrix}^{T} \nonumber\]
respectivamente. A los efectos de nuestro ejemplo suponemos que cada uno\(k_{j} = 1\) excepto\(k_{8} = 5\). Ensamblamos\(A^{T}KA\) como en el Capítulo 2 y resolvemos
\[A^{T}KAx^{j} = f^{j} \nonumber\]
con la ayuda de la pseudoinversa. Para impartir cierta `realidad' a este problema, contaminamos cada uno\(x^{j}\) con un 10 por ciento de ruido antes de construir\(B\)
\[B^{T}Bk = B^{T}f \nonumber\]
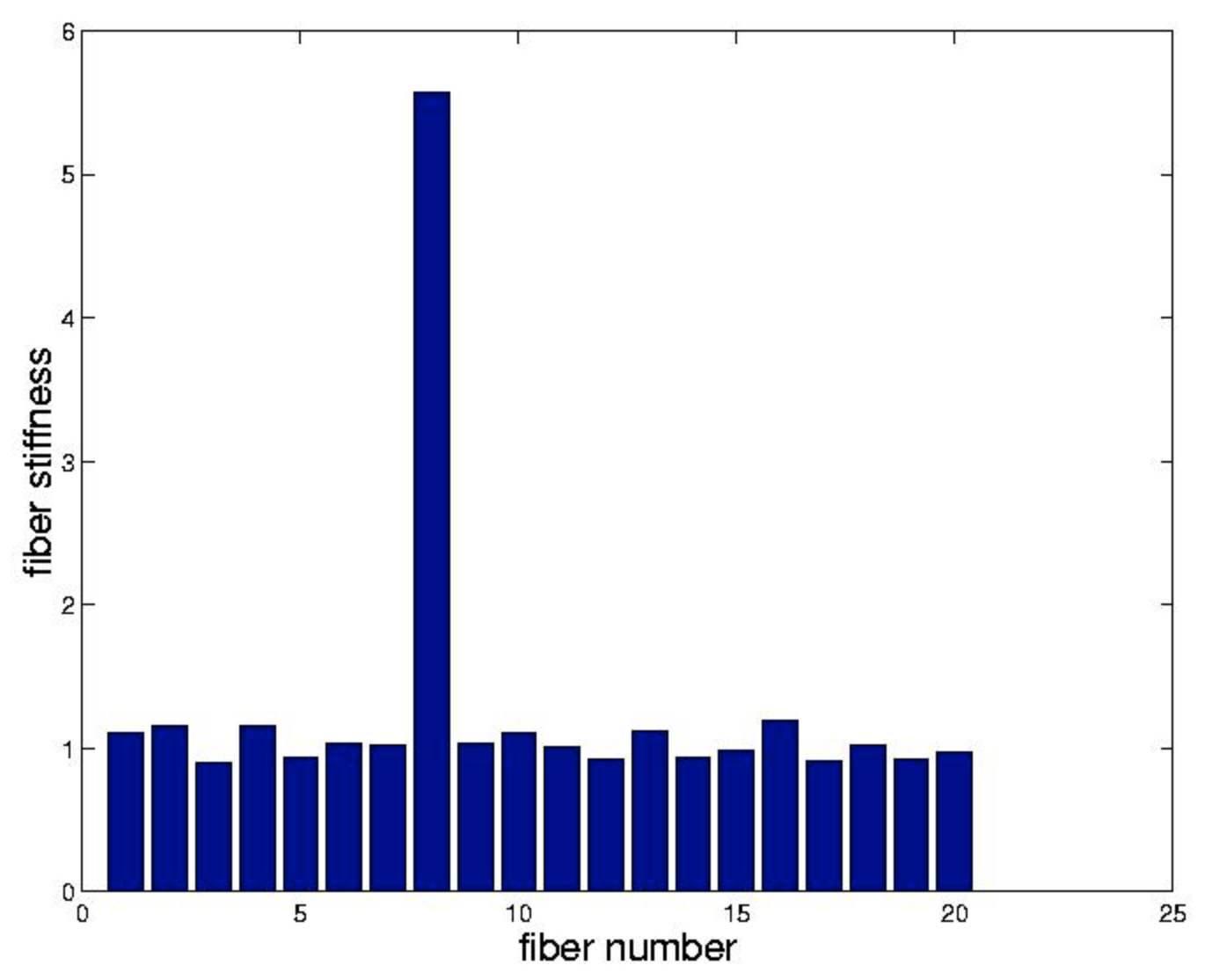
observamos que Matlab resuelve este sistema cuando se presenta con K=b\ f cuando BB es rectangular. Hemos trazado los resultados de este procedimiento en el enlace. La fibra rígida se identifica fácilmente.
Proyecciones
Desde un punto de vista algebraico La ecuación es una elegante reformulación del problema de mínimos cuadrados. Aunque fácil de recordar, desgraciadamente oscurece el contenido geométrico, sugerido por la palabra 'proyección', de Ecuación. Como las proyecciones surgen frecuentemente en muchas aplicaciones hacemos una pausa aquí para desarrollarlas con más cuidado. Con respecto a las ecuaciones normales observamos que si\(\mathbb{N}(A) = \{0\}\) entonces
\[x = (A^{T}A)^{-1} A^{T} b \nonumber\]
y así la proyección ortogonal de bb sobre\(\mathbb{R}(A)\) es:
\[b_{R}= Ax \nonumber\]
\[= A (A^{T}A)^{-1} A^T b \nonumber\]
Definiendo
\[P = A (A^{T}A)^{-1} A^T \nonumber\]
toma la forma\(b_{R} = Pb\). De acuerdo con nuestra noción de lo que debería ser una 'proyección', esperamos que\(P\) mapee vectores que no estén dentro\(\mathbb{R}(A)\) mientras dejan vectores ya\(\mathbb{R}(A)\) ilesos.\(\mathbb{R}(A)\) De manera más sucinta, esperamos que\(Pb_{R} = b_{R}\) i.e\(Pb_{R} = Pb_{R}\).,. Como este último debe sostenerse para todos\(b \in R^{m}\) esperamos que
\[P^2 = P \nonumber\]
Encontramos que de hecho
\[P^2 = A (A^{T}A)^{-1} A^T A (A^{T}A)^{-1} A^T \nonumber\]
\[= A (A^{T}A)^{-1} A^T \nonumber\]
\[= P \nonumber\]
También observamos que el\(P\) es simétrico. Dignificamos estas propiedades a través de
Una matriz\(P\) que satisface\(P^2 = P\) se llama proyección. Una proyección simétrica se denomina proyección ortogonal.
Nos hemos esforzado por motivar el uso de la palabra 'proyección'. Quizás se esté preguntando sin embargo qué tiene que ver la simetría con la ortogonalidad. Esto lo explicamos en términos de la tautología
\[b = Pb−Ib \nonumber\]
Ahora bien, si\(P\) es una proyección entonces también lo es\(I-P\). Además, si\(P\) es simétrico entonces el punto producto de\(b\).
\ [\ begin {align*} (Pb) ^T (I-P) b &= b^ {T} P^ {T} (I-P) b\\ [4pt] &= b^ {T} (P-P^ {2}) b\\ [4pt] &= b^ {T} 0 b\\ [4pt] &= 0\ end {align*}
es decir,\(Pb\) es ortogonal a\((I-P)b\). Como ejemplos de proyecciones no ortogonales ofrecemos
\[P = \begin{pmatrix} {1}&{0}&{0}\\ {\frac{-1}{2}}&{0}&{0}\\ {\frac{-1}{4}}&{\frac{-1}{2}}&{1} \end{pmatrix}\]
y\(I-P\). Por último, señalemos que la fórmula central\(P = A (A^{T}A)^{-1} A^T\), es incluso un poco más general de lo que se anuncia. Se ha facturado como la proyección ortogonal sobre el espacio de columna de\(A\). Sin embargo, a menudo surge la necesidad de la proyección ortogonal sobre algún subespacio arbitrario M. La clave para usar el PP antiguo es simplemente darse cuenta de que cada subespacio es el espacio de columna de alguna matriz. Más precisamente, si
\[\{x_{1}, \cdots, x_{m}\} \nonumber\]
es una base para MM entonces claramente si estos\(x_{j}\) se colocan en las columnas de una matriz llamada\(A\) entonces\(\mathbb{R}(A) = M\). Por ejemplo, si\(M\) es la línea a través de\(\begin{pmatrix} {1}&{1} \end{pmatrix}^{T}\) entonces
\[P = \begin{pmatrix} {1}\\ {1} \end{pmatrix} \frac{1}{2} \begin{pmatrix} {1}&{1} \end{pmatrix} \nonumber\]
\[P = \frac{1}{2} \begin{pmatrix} {1}&{1}\\ {1}&{1} \end{pmatrix} \nonumber\]
es proyección ortogonal sobre\(M\).
Ejercicios
Gilbert Strang se estiró sobre una rejilla a longitudes\(l = 6, 7, 8\) pies bajo fuerzas aplicadas de\(f = 1, 2, 4\) toneladas. Asumiendo la ley de Hooke\(l−L = cf\), encuentra su cumplimiento\(c\),, y altura original\(L\),, por mínimos cuadrados.
Con respecto al ejemplo del § 3 señalar que, debido a la generación aleatoria del ruido que mancha los desplazamientos, se obtiene una 'respuesta' diferente cada vez que se invoca el código.
- Escriba un bucle que invoque el código un número de veces estadísticamente significativo y envíe gráficas de barras de la rigidez promedio de la fibra y su desviación estándar para cada fibra, junto con el archivo M asociado.
- Experimentar con diversos niveles de ruido con el objetivo de determinar el nivel por encima del cual se hace difícil discernir la fibra rígida. Explique cuidadosamente sus hallazgos.
Encuentra la matriz que\(\mathbb{R}^3\) proyecta en la línea abarcada por\(\begin{pmatrix} {1}&{0}&{1} \end{pmatrix}^{T}\).
Encuentra la matriz que\(\mathbb{R}^3\) proyecta en la línea abarcada por\(\begin{pmatrix} {1}&{0}&{1} \end{pmatrix}^{T}\) y\(\begin{pmatrix} {1}&{1}&{-1} \end{pmatrix}^{T}\).
Si\(P\) es la\(\mathbb{R}^m\) proyección de un subespacio k—dimensional\(M\), ¿cuál es el rango\(P\) y cuál es\(\mathbb{R}(P)\)?