4.9: El Producto Cruzado
- Page ID
- 114514
- Compute el producto cruzado y el producto de caja de vectores en\(\mathbb{R}^3\).
Recordemos que el producto punto es uno de los dos productos importantes para vectores. El segundo tipo de producto para vectores se llama el producto cruzado. Es importante señalar que el producto cruzado solo se define en\(\mathbb{R}^{3}.\) Primero discutimos el significado geométrico y luego se da una descripción en términos de coordenadas, ambas de las cuales son importantes. La descripción geométrica es esencial para comprender las aplicaciones a la física y la geometría, mientras que la descripción de coordenadas es necesaria para calcular el producto cruzado.
Considera la siguiente definición.
Tres vectores,\(\vec{u},\vec{v},\vec{w}\) forman un sistema de mano derecha si cuando extiendes los dedos de tu mano derecha a lo largo de la dirección del vector\(\vec{u}\) y los cierras en la dirección de\(\vec{v}\), el pulgar apunta aproximadamente en la dirección de\(\vec{w}\).
Para ver un ejemplo de un sistema de vectores diestros, vea la siguiente imagen.
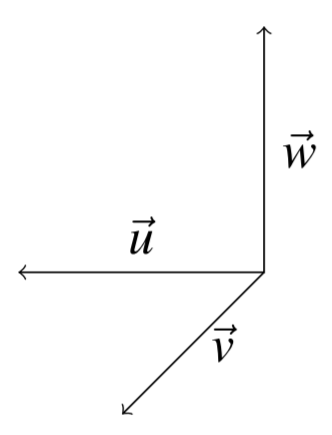
En esta imagen el vector\(\vec{w}\) apunta hacia arriba desde el plano determinado por los otros dos vectores. Apunta los dedos de tu mano derecha a lo largo\(\vec{u}\), y ciérralos en la dirección de\(\vec{v}\). Observe que si extiende el pulgar sobre su mano derecha, apunta en la dirección de\(\vec{w}\).
Debe considerar en qué se diferenciaría un sistema de mano derecha de un sistema de mano izquierda. Intenta usar tu mano izquierda y verás que el vector\(\vec{w}\) necesitaría apuntar en dirección opuesta.
Observe que los vectores especiales, siempre\(\vec{i},\vec{j},\vec{k}\) formarán un sistema diestro. Si extiende los dedos de su mano derecha\(\vec{i}\) y los cierra en la dirección\(\vec{j}\), el pulgar apunta en la dirección de\(\vec{k}\).
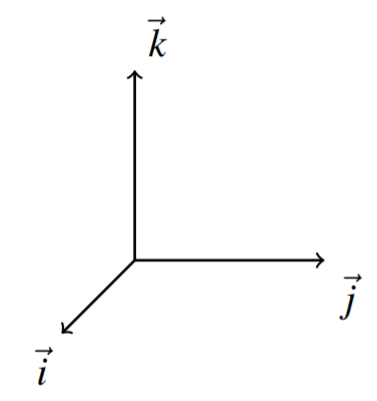
A continuación se presenta la descripción geométrica del producto cruzado. Recordemos que el producto punto de dos vectores da como resultado un escalar. En contraste, el producto cruzado da como resultado un vector, ya que el producto da una dirección así como una magnitud.
Dejar\(\vec{u}\) y\(\vec{v}\) ser dos vectores en\(\mathbb{R}^{3}.\) Entonces el producto cruzado, escrito\(\vec{u}\times \vec{v}\), se define por las siguientes dos reglas.
- Su longitud es\[\| \vec{u}\times \vec{v}\| =\| \vec{u}\| \| \vec{v}\| \sin \theta, \nonumber \] donde\(\theta\) está el ángulo incluido entre\(\vec{u}\) y\(\vec{v}\).
- Es perpendicular a ambos\(\vec{u}\) y\(\vec{v}\), es decir\[\left( \vec{u}\times \vec{v} \right) \cdot \vec{u}=0, \]\[\left( \vec{u}\times \vec{v} \right) \cdot \vec{v}=0, \nonumber\] y\[\vec{u},\vec{v},\vec{u}\times \vec{v} \nonumber\] formar un sistema de mano derecha.
El producto cruzado de los vectores especiales\(\vec{i}, \vec{j}, \vec{k}\) es el siguiente. \[\begin{array}{cc} \vec{i}\times \vec{j}=\vec{k} & \vec{j}\times \vec{i}=-\vec{k} \\ \vec{k}\times \vec{i}=\vec{j} & \vec{i}\times \vec{k}=-\vec{j} \\ \vec{j}\times \vec{k}=\vec{i} & \vec{k}\times \vec{j}=-\vec{i} \end{array}\nonumber \]Con esta información, a continuación se da la descripción coordinada del producto cruzado.
Recordemos que el vector se\(\vec{u}= \left[ \begin{array}{ccc} u_1 & u_2 & u_3 \end{array} \right]^T\) puede escribir en términos de\(\vec{i}, \vec{j}, \vec{k}\) as\(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\).
Dejar\(\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\) y\(\vec{v}=v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\) ser dos vectores. Entonces
\[\begin{array}{c} \vec{u}\times \vec{v} =\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3} - u_{3}v_{1}\right) \vec{j}+ \left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \label{crossprod1} \end{array}\]
Escribiendo\(\vec{u} \times \vec{v}\) de la manera habitual, viene dada por
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} u_{2}v_{3}-u_{3}v_{2} \\ -(u_{1}v_{3}-u_{3}v_{1}) \\ u_{1}v_{2}-u_{2}v_{1} \end{array} \right]\nonumber \]
Ahora probamos esta proposición.
- Prueba
-
De la tabla anterior y las propiedades del producto cruzado enumerado,\[\begin{aligned} \vec{u} \times \vec{v} &= \left( u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\right) \times \left( v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\right) \\ &= u_{1}v_{2}\vec{i}\times \vec{j}+u_{1}v_{3}\vec{i}\times \vec{k}+u_{2}v_{1}\vec{j}\times \vec{i}+ u_{2}v_{3}\vec{j}\times \vec{k}+ +u_{3}v_{1}\vec{k}\times \vec{i}+u_{3}v_{2}\vec{k}\times \vec{j} \\ &=u_{1}v_{2}\vec{k}-u_{1}v_{3}\vec{j}-u_{2}v_{1}\vec{k}+u_{2}v_{3} \vec{i}+u_{3}v_{1}\vec{j}-u_{3}v_{2}\vec{i} \\ &=\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}+\left( u_{3}v_{1}-u_{1}v_{3}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \end{aligned}\]\[\label{crossprod2}\]
Hay otra versión de la\(\eqref{crossprod1}\) cual puede ser más fácil de recordar. Podemos expresar el producto cruzado como determinante de una matriz, de la siguiente manera.
\[\vec{u}\times \vec{v} = \left\vert \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{array} \right\vert \label{crossprod3}\]Expandiendo el determinante a lo largo de la fila superior rinde\[\vec{i}\left( -1\right) ^{1+1}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert +\vec{j}\left( -1\right) ^{2+1}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left( -1\right) ^{3+1}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber \]\
\[=\vec{i}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert -\vec{j}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber \]
Ampliar estos determinantes lleva a\[\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3}-u_{3}v_{1}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \nonumber \] que es lo mismo que\(\eqref{crossprod2}\).
El producto cruzado satisface las siguientes propiedades.
Dejar\(\vec{u}, \vec{v}, \vec{w}\) ser vectores adentro\(\mathbb{R}^3\), y\(k\) un escalar. Entonces, se mantienen las siguientes propiedades del producto cruzado.
- \(\vec{u}\times \vec{v}= -\left( \vec{v}\times \vec{u}\right), \mbox{and} \; \vec{u}\times \vec{u}=\vec{0}\)
- \(\left( k \vec{u}\right)\times \vec{v}= k \left( \vec{u}\times \vec{v}\right) =\vec{u}\times \left( k \vec{v}\right)\)
- \(\vec{u}\times \left( \vec{v}+\vec{w}\right) =\vec{u}\times \vec{v}+\vec{u}\times \vec{w}\)
- \(\left( \vec{v}+\vec{w}\right) \times \vec{u}=\vec{v} \times \vec{u}+\vec{w}\times \vec{u}\)
- Prueba
-
La fórmula\(1.\) se desprende inmediatamente de la definición. Los vectores\(\vec{u}\times \vec{v}\) y\(\vec{v}\times \vec{u}\) tienen la misma magnitud,\(\left\vert \vec{u}\right\vert \left\vert \vec{v}\right\vert \sin \theta ,\) y una aplicación de la regla de la mano derecha muestra que tienen dirección opuesta.
\(2.\)La fórmula está probada de la siguiente manera. Si\(k\) es un escalar no negativo, la dirección de\(\left( k \vec{u}\right) \times \vec{v}\) es la misma que la dirección de\(\vec{u}\times \vec{v}, k \left( \vec{u}\times \vec{v}\right)\) y\(\vec{u}\times \left( k \vec{v}\right)\). La magnitud es\(k\) por la magnitud de la\(\vec{u}\times \vec{v}\) cual es la misma que la magnitud de\(k \left( \vec{u}\times \vec{v}\right)\) y El\(\vec{u}\times \left( k \vec{v}\right) .\) uso de esto produce igualdad en\(2\). En el caso en\(k <0,\) que todo funcione de la misma manera excepto los vectores están todos apuntando en dirección opuesta y debes multiplicar por\(\left\vert k \right\vert\) al comparar sus magnitudes.
Las leyes distributivas,\(3.\) y\(4.\), son mucho más difíciles de establecer. Por ahora, basta con notar que si sabemos que eso\(3.\) es cierto,\(4.\) sigue. Así, asumiendo\(3.\), y utilizando\(1.\),\[\begin{aligned} \left( \vec{v}+\vec{w}\right) \times \vec{u}& =-\vec{u}\times \left( \vec{v}+\vec{w}\right) \\ & =-\left( \vec{u}\times \vec{v}+\vec{u}\times \vec{w}\right) \\ & =\vec{v}\times \vec{u}+\vec{w}\times \vec{u}\end{aligned}\]
Ahora veremos un ejemplo de cómo calcular un producto cruzado.
Encuentra\(\vec{u} \times \vec{v}\) los siguientes vectores
\[\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber \]
Solución
Tenga en cuenta que podemos escribir\(\vec{u}, \vec{v}\) en términos de los vectores especiales\(\vec{i}, \vec{j}, \vec{k}\) como
\[\begin{array}{c} \vec{u} = \vec{i}-\vec{j}+2\vec{k} \\ \vec{v} = 3\vec{i}-2\vec{j}+\vec{k} \end{array}\nonumber \]
Utilizaremos la ecuación dada por\(\eqref{crossprod3}\) para calcular el producto cruzado.
\[\vec{u} \times \vec{v} = \left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & -1 & 2 \\ 3 & -2 & 1 \end{array} \right\vert =\left\vert \begin{array}{rr} -1 & 2 \\ -2 & 1 \end{array} \right\vert \vec{i}-\left\vert \begin{array}{rr} 1 & 2 \\ 3 & 1 \end{array} \right\vert \vec{j}+\left\vert \begin{array}{rr} 1 & -1 \\ 3 & -2 \end{array} \right\vert \vec{k}=3\vec{i}+5\vec{j}+\vec{k}\nonumber \]
Podemos escribir este resultado de la manera habitual, como\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber \]
Una aplicación geométrica importante del producto cruzado es la siguiente. El tamaño del producto cruzado,\(\| \vec{u}\times \vec{v}\|\), es el área del paralelogramo determinada por\(\vec{u}\) y\(\vec{v}\), como se muestra en la siguiente imagen.
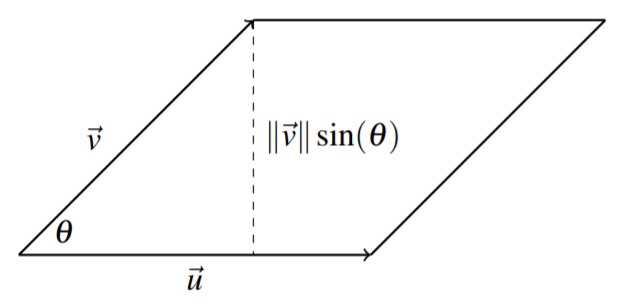
Examinamos este concepto en el siguiente ejemplo.
Encuentra el área del paralelogramo determinada por los vectores\(\vec{u}\) y\(\vec{v}\) dada por
\[\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber \]
Solución
Observe que estos vectores son los mismos que los dados en Ejemplo\(\PageIndex{1}\). Recordemos de la descripción geométrica del producto cruzado, que el área del paralelogramo es simplemente la magnitud de\(\vec{u} \times \vec{v}\). De Ejemplo\(\PageIndex{1}\),\(\vec{u} \times \vec{v} = 3\vec{i}+5\vec{j}+\vec{k}\). También podemos escribir esto como
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber \]
Así el área del paralelogramo es
\[\| \vec{u} \times \vec{v} \| = \sqrt{(3)(3) + (5)(5) + (1)(1)} = \sqrt{9+25+1}=\sqrt{35}\nonumber \]
También podemos utilizar este concepto para encontrar el área de un triángulo. Considera el siguiente ejemplo.
Encuentra el área del triángulo determinada por los puntos\(\left(1, 2, 3 \right) , \left( 0,2,5\right), \left( 5,1, 2 \right)\)
Solución
Este triángulo se obtiene conectando los tres puntos con líneas. Picking\(\left( 1,2,3\right)\) como punto de partida, hay dos vectores de desplazamiento,\(\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T\) y\(\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T\). Observe que si agregamos cualquiera de estos vectores al vector de posición del punto de partida, el resultado son los vectores de posición de los otros dos puntos. Ahora, el área del triángulo es la mitad del área del paralelogramo determinado por\(\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T\) y\(\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T.\) El producto cruzado requerido viene dado por
\[\left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right] \times \left[ \begin{array}{r} 4 \\ -1 \\ -1 \end{array} \right] = \left[ \begin{array}{rrr} 2 & 7 & 1 \end{array} \right]\nonumber \]
Tomando el tamaño de este vector da el área del paralelogramo, dada por
\[\sqrt{(2)(2) + (7)(7) + (1)(1)} = \sqrt{4+49+1} = \sqrt{54}\nonumber \]De ahí que el área del triángulo sea\(\frac{1}{2}\sqrt{54}= \frac{3}{2}\sqrt{6}.\)
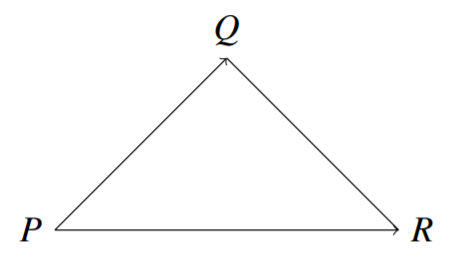
En general, si tienes tres puntos adentro\(\mathbb{R}^{3}, P,Q,R\), el área del triángulo viene dada por\[\frac{1}{2}\| \vec{PQ} \times \vec{PR} \|\nonumber \]
Recordemos que\(\vec{PQ}\) es el vector que va de punto\(P\) a punto\(Q\).
En la siguiente sección, exploramos otra aplicación del producto cruzado.
El producto de la caja
Recordemos que podemos utilizar el producto cruzado para encontrar el área de un paralelogramo. De ello se deduce que podemos utilizar el producto cruzado junto con el producto punto para encontrar el volumen de un paralelepípedo. Comenzamos con una definición.
Un paralelepípedo determinado por los tres vectores,\(\vec{u},\vec{v}\), y\(\vec{w}\) consiste en\[\left\{ r\vec{u}+s\vec{v}+t\vec{w}:r,s,t\in \left[ 0,1\right] \right\}\nonumber \]
Es decir, si eliges tres números,\(r,s,\) y\(t\) cada uno en\(\left[ 0,1\right]\) y forma\(r\vec{u}+s\vec{v}+t\vec{w}\) entonces la colección de todos esos puntos constituye el paralelepípedo determinado por estos tres vectores.
El siguiente es un ejemplo de un paralelepípedo.
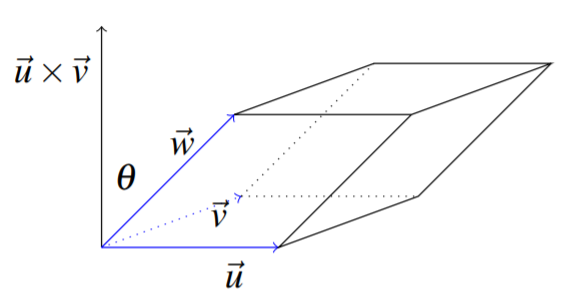
Observe que la base del paralelepípedo es el paralelogramo determinado por los vectores\(\vec{u}\) y\(\vec{v}\). Por lo tanto, su área es igual a\(\| \vec{u}\times \vec{v} \|\). La altura del paralelepípedo es\(\| \vec{w}\| \cos \theta\) donde\(\theta\) está el ángulo que se muestra en la imagen entre\(\vec{w}\) y\(\vec{u}\times \vec{v}\). El volumen de este paralelepípedo es el área de la base multiplicada por la altura que es justo\[\| \vec{u}\times \vec{v}\| \| \vec{w}\| \cos \theta = \left( \vec{u}\times\vec{v}\right) \cdot \vec{w}\nonumber \] Esta expresión se conoce como el producto de la caja y a veces se escribe como\(\left[ \vec{u},\vec{v},\vec{w}\right] .\) Deberías considerar lo que sucede si te intercambias el\(\vec{v}\) con el\(\vec{w}\) o el\(\vec{u}\) con el \(\vec{w}\). Se puede ver geométricamente a partir del dibujo de imágenes que esto simplemente introduce un signo menos. En cualquier caso la caja producto de tres vectores siempre es igual o bien al volumen del paralelepípedo determinado por los tres vectores o bien\(-1\) multiplicado por este volumen.
Dejan\(\vec{u}, \vec{v}, \vec{w}\) ser tres vectores en\(\mathbb{R}^n\) los que definen un paralelepípedo. Entonces el volumen del paralelepípedo es el valor absoluto del producto de caja, dado por\[\left| \left(\vec{u}\times\vec{v}\right) \cdot \vec{w} \right|\nonumber \]
Consideremos un ejemplo de este concepto.
Encuentra el volumen del paralelepípedo determinado por los vectores
\[\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right], \vec{w} = \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right]\nonumber \]
Solución
De acuerdo con la discusión anterior, escoge cualquiera de estos vectores, toma el producto cruzado y luego toma el producto punto de este con el tercero de estos vectores. El resultado será el volumen deseado o\(-1\) veces el volumen deseado. Por lo tanto, al tomar el valor absoluto del resultado, obtenemos el volumen.
Tomaremos el producto cruzado de\(\vec{u}\) y\(\vec{v}\). Esto viene dado por
\[\vec{u} \times \vec{v} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right] \times \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right]\nonumber \]\[=\left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & 2 & -5 \\ 1 & 3 & -6 \end{array} \right\vert = 3\vec{i}+\vec{j}+\vec{k} = \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right]\nonumber \]
Ahora toma el punto producto de este vector con el\(\vec{w}\) que rinde\[\begin{aligned} (\vec{u} \times \vec{v}) \cdot \vec{w} &= \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right] \cdot \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right] \\ &=\left( 3\vec{i}+\vec{j}+\vec{k}\right) \cdot \left( 3\vec{i}+2\vec{j}+3\vec{k}\right) \\ &=9+2+3 \\ &=14\end{aligned}\]
Esto muestra que el volumen de este paralelepípedo es de 14 unidades cúbicas.
Hay una observación fundamental que proviene directamente de las definiciones geométricas del producto cruzado y el producto de punto.
Dejar\(\vec{u},\vec{v}\), y\(\vec{w}\) ser vectores. Entonces\(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}=\vec{u}\cdot \left( \vec{v}\times \vec{w} \right) .\)
- Prueba
-
Esto se deduce de observar que cualquiera\(\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}\) y\(\vec{u}\cdot \left( \vec{v}\times \vec{w}\right)\) ambos dan el volumen del paralelepípedo o ambos dan\(-1\) veces el volumen.
Recordemos que podemos expresar el producto cruzado como el determinante de una matriz particular. Resulta que lo mismo se puede hacer para el producto de caja. Supongamos que tiene tres vectores,\(\vec{u}=\left[ \begin{array}{rrr} a & b & c \end{array} \right]^T ,\vec{v}=\left[ \begin{array}{rrr} d & e & f \end{array} \right]^T ,\) y\(\vec{w}=\left[ \begin{array}{rrr} g & h & i \end{array} \right]^T .\) Entonces el producto de caja\(\vec{u}\cdot \left(\vec{v}\times \vec{w}\right)\) viene dado por lo siguiente. \[\begin{aligned} \vec{u}\cdot \left(\vec{v}\times \vec{w}\right) &= \left[ \begin{array}{r} a \\ b \\ c \end{array} \right] \cdot \left| \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ d & e & f \\ g & h & i \end{array} \right| \\ &=a\left| \begin{array}{rr} e & f \\ h & i \end{array} \right| -b\left| \begin{array}{rr} d & f \\ g & i \end{array} \right| +c\left| \begin{array}{rr} d & e \\ g & h \end{array} \right| \\ &= \det \left[ \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \right] \end{aligned}\]
Para tomar el producto de caja, simplemente puede tomar el determinante de la matriz que resulta dejando que las filas sean los componentes de los vectores dados en el orden en que ocurren en el producto de caja.
Esto se desprende directamente de la definición del producto cruzado dada anteriormente y de la forma en que expandimos los determinantes. Así, el volumen de un paralelepípedo determinado por los vectores\(\vec{u},\vec{v},\vec{w}\) es solo el valor absoluto del determinante anterior.


