3.4: Números Complejos
- Page ID
- 113923
Con todas las operaciones definidas en §§1-3, aún no\(E^{n}(n>1)\) es un campo por la falta de multiplicación vectorial que satisfagan los axiomas de campo. Ahora vamos a definir tal multiplicación, pero sólo para\(E^{2} .\) Así se\(E^{2}\) convertirá en un campo, al que llamaremos el campo complejo,\(C .\)
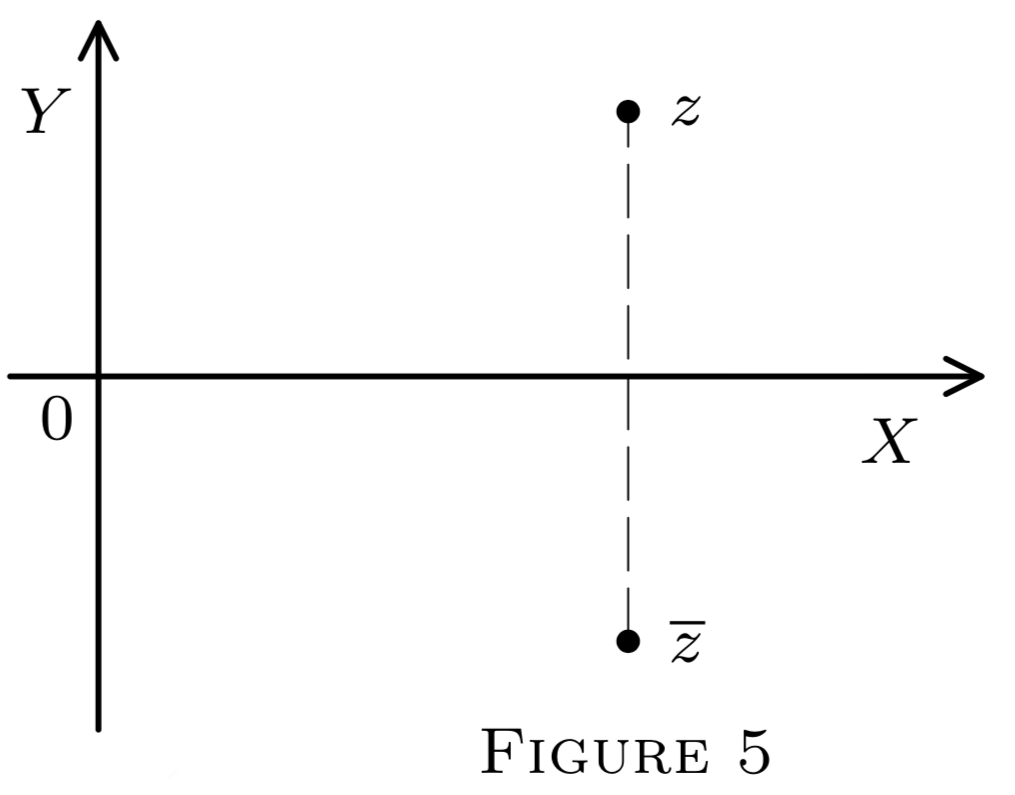
Aquí hacemos algunos cambios en la notación y terminología. Los puntos de\(E^{2},\) cuando se consideran elementos de se\(C,\) llamarán números complejos (siendo cada uno un par ordenado de números reales). Los denotamos por letras simples (preferiblemente z) sin barra ni flecha. Por ejemplo,\(z=(x, y)\). Preferiblemente escribimos\((x, y)\) para\(\left(x_{1}, x_{2}\right) .\) Si\(z=(x, y),\) entonces\(x\) y\(y\) se llaman las partes real e imaginaria de\(z,\) respectivamente,\(^{1}\) y\(\overline{z}\) denota el número complejo\((x,-y),\) llamado el conjugado de\(z\) (ver Figura 5\()\).
Los números complejos con parte imaginaria desaparecida,\((x, 0),\) se llaman puntos reales de\(C .\) Para brevedad, simplemente escribimos\(x\)\((x, 0) ;\) por ejemplo,\(2=(2,0)\). En particular,\(1=(1,0)=\overline{\theta}_{1}\) se llama la unidad real en\(C .\) Puntos con parte real desaparecida,\((0, y),\) se llaman números (puramente) imaginarios. En particular,\(\overline{\theta}_{2}=(0,1)\) es tal número; ahora lo vamos a denotar por\(i\) y llamarlo la unidad imaginaria en\(C .\) Aparte de estas peculiaridades, todas nuestras definiciones anteriores de §§1-3 siguen siendo válidas\(E^{2}=C .\) en En particular, si\(z=(x, y)\) y\(z^{\prime}=\left(x^{\prime}, y^{\prime}\right),\) tenemos
\[z \pm z^{\prime}=(x, y) \pm\left(x^{\prime}, y^{\prime}\right)=\left(x \pm x^{\prime}, y \pm y^{\prime}\right),\]
\[\rho\left(z, z^{\prime}\right)=\sqrt{\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}}, \text{ and} \]
\[|z|=\sqrt{x^{2}+y^{2}}.\]
Todos los teoremas de §§1-3 son válidos.
Ahora definimos la nueva multiplicación en la\(C,\) que la hará un campo.
\[\text{If } z=(x, y) \text{ and } z^{\prime}=\left(x^{\prime}, y^{\prime}\right), \text{ then } z z^{\prime}=\left(x x^{\prime}-y y^{\prime}, x y^{\prime}+y x^{\prime}\right).\]
\(E^{2}=C\)es un campo, con cero elemento\(0=(0,0)\) y unidad\(1=(1, 0)\), bajo suma y multiplicación como se definió anteriormente.
- Prueba
-
Sólo debemos demostrar que la multiplicación obedece a los axiomas 1-6 de los axiomas de campo. Tenga en cuenta que para la adición, todo está probado en el Teorema 1 de §§1-3.
El axioma 1 (cierre) es obvio a partir de nuestra definición, porque si\(z\) y\(z^{\prime}\) están en\(C,\) así es\(z z^{\prime}\).
Para probar la conmutatividad, tomar cualquier número complejo
\[z=(x, y) \text{ and } z^{\prime}=\left(x^{\prime}, y^{\prime}\right)\]
y verificar que\(z z^{\prime}=z^{\prime} z .\) Efectivamente, por definición,
\[z z^{\prime}=\left(x x^{\prime}-y y^{\prime}, x y^{\prime}+y x^{\prime}\right) \text{ and } z^{\prime} z=\left(x^{\prime} x-y^{\prime} y, x^{\prime} y+y^{\prime} x\right);\]
pero las dos expresiones coinciden por las leyes conmutativas para números reales. La asociatividad y distributividad se prueban de manera similar.
A continuación, mostramos que\(1=(1,0)\) satisface el Axioma 4 (b), es decir, que\(1 z=z\) para cualquier número complejo\(z=(x, y) .\) De hecho, por definición, y por axiomas para\(E^{1}\),
\[1 z=(1,0)(x, y)=(1 x-0 y, 1 y+0 x)=(x-0, y+0)=(x, y)=z.\]
Queda por verificar el Axioma 5 (b), es decir, mostrar que cada número complejo\(z=(x, y) \neq(0,0)\) tiene una inversa\(z^{-1}\) tal que\(z z^{-1}=1 .\) resulta que la inversa se obtiene configurando
\[z^{-1}=\left(\frac{x}{|z|^{2}},-\frac{y}{|z|^{2}}\right).\]
De hecho, entonces obtenemos
\[z z^{-1}=\left(\frac{x^{2}}{|z|^{2}}+\frac{y^{2}}{|z|^{2}},-\frac{x y}{|z|^{2}}+\frac{y x}{|z|^{2}}\right)=\left(\frac{x^{2}+y^{2}}{|z|^{2}}, 0\right)=(1,0)=1\]
ya que\(x^{2}+y^{2}=|z|^{2},\) por definición. Esto completa la prueba. \(\square\)
\(i^{2}=-1 ; i . e .,(0,1)(0,1)=(-1,0)\).
- Prueba
-
Por definición,\((0,1)(0,1)=(0 \cdot 0-1 \cdot 1,0 \cdot 1+1 \cdot 0)=(-1,0)\).
Así\(C\) tiene un elemento\(i\) cuyo cuadrado es\(-1,\) mientras que no\(E^{1}\) tiene tal elemento, por Corolario 2 en Capítulo\(2,8\{1-4 .\) Esto no es contradicción ya que ese corolario se sostiene únicamente en campos ordenados. Sólo muestra que\(C\) no se puede hacer un campo ordenado.
Sin embargo, los “puntos reales”\(C\) forman un subcampo que se puede ordenar estableciendo
\[(x, 0)<\left(x^{\prime}, 0\right) \text{ iff } x<x^{\prime} \text{ in } E^{1} .\]
Entonces este subcampo se comporta exactamente como\(E^{1} .\) Por lo tanto, es costumbre no distinguir entre “puntos reales en\(C^{\prime \prime}\) y “números reales”, identificándose\((x, 0)\)\(x .\) con Con esta convención,\(E^{1}\) simplemente es un subconjunto\((\) y un subcampo\()\) de En\(C .\) adelante, simplemente diremos que “x es real” o “x\(\in E^{1 \prime}\) en lugar de"\(x =(x, 0)\) es un punto real”. Luego obtenemos el siguiente resultado.
Cada uno\(z \in C\) tiene una representación única como
\[z=x+y i,\]
donde\(x\) y\(y\) son reales y\(i=(0,1) .\) Específicamente,
\[z=x+y i \text{ iff } z=(x, y).\]
- Prueba
-
Por nuestras convenciones,\(x=(x, 0)\) y\(y=(y, 0),\) así
\[x+y i=(x, 0)+(y, 0)(0,1).\]
Computando la expresión de la derecha a partir de definiciones, tenemos para cualquiera\(x, y \in E^{1}\) que
\[x+y i=(x, 0)+(y \cdot 0-0 \cdot 1, y \cdot 1+0 \cdot 1)=(x, 0)+(0, y)=(x, y).\]
Así\((x, y)=x+y i\) para cualquier\(x, y \in E^{1} .\) En particular, si\((x, y)\) es el número dado\(z \in C\) del teorema, obtenemos\(z=(x, y)=x+y i,\) según se requiera.
Para probar la singularidad, supongamos que también tenemos
\[z=x^{\prime}+y^{\prime} i \text{ with } x^{\prime}=\left(x^{\prime}, 0\right) \text{ and } y^{\prime}=\left(y^{\prime}, 0\right).\]
Entonces, como se muestra arriba,\(z=\left(x^{\prime}, y^{\prime}\right) .\) ya que también\(z=(x, y),\) tenemos\((x, y)= \left(x^{\prime}, y^{\prime}\right),\) i.e., los dos pares ordenados coinciden, y así\(x=x^{\prime}\) y\(y=y^{\prime}\) después de todo. \(\square\)
Geométricamente, en lugar de coordenadas cartesianas también\((x, y),\) podemos usar coordenadas polares\(r, \theta,\) donde
\[r=\sqrt{x^{2}+y^{2}}=|z|\]
y\(\theta\) es el ángulo de rotación (en sentido contrario a las agujas del reloj) desde el\(x\) eje -eje a la línea dirigida\(\overrightarrow{0 z} ;\) ver Figura\(6 .\) Claramente,\(z\) está determinado de manera única por\(r\) y\(\theta\) pero no\(\theta\) está determinado únicamente por de\(z ;\) hecho, el mismo punto de\(E^{2}\) resultados si\(\theta\) es reemplazado por\(\theta+2 n \pi(n=1,2, \ldots)\). (Si\(z=0,\) entonces no\(\theta\) está definido en absoluto.) Los valores\(r\) y\(\theta\) se denominan, respectivamente, el módulo y argumento de\(z=(x, y) .\) Por trigonometría elemental,\(x=r \cos \theta\) y\(y=r \sin \theta .\) Sustituyendo en\(z=x+y i,\) obtenemos el siguiente corolario.
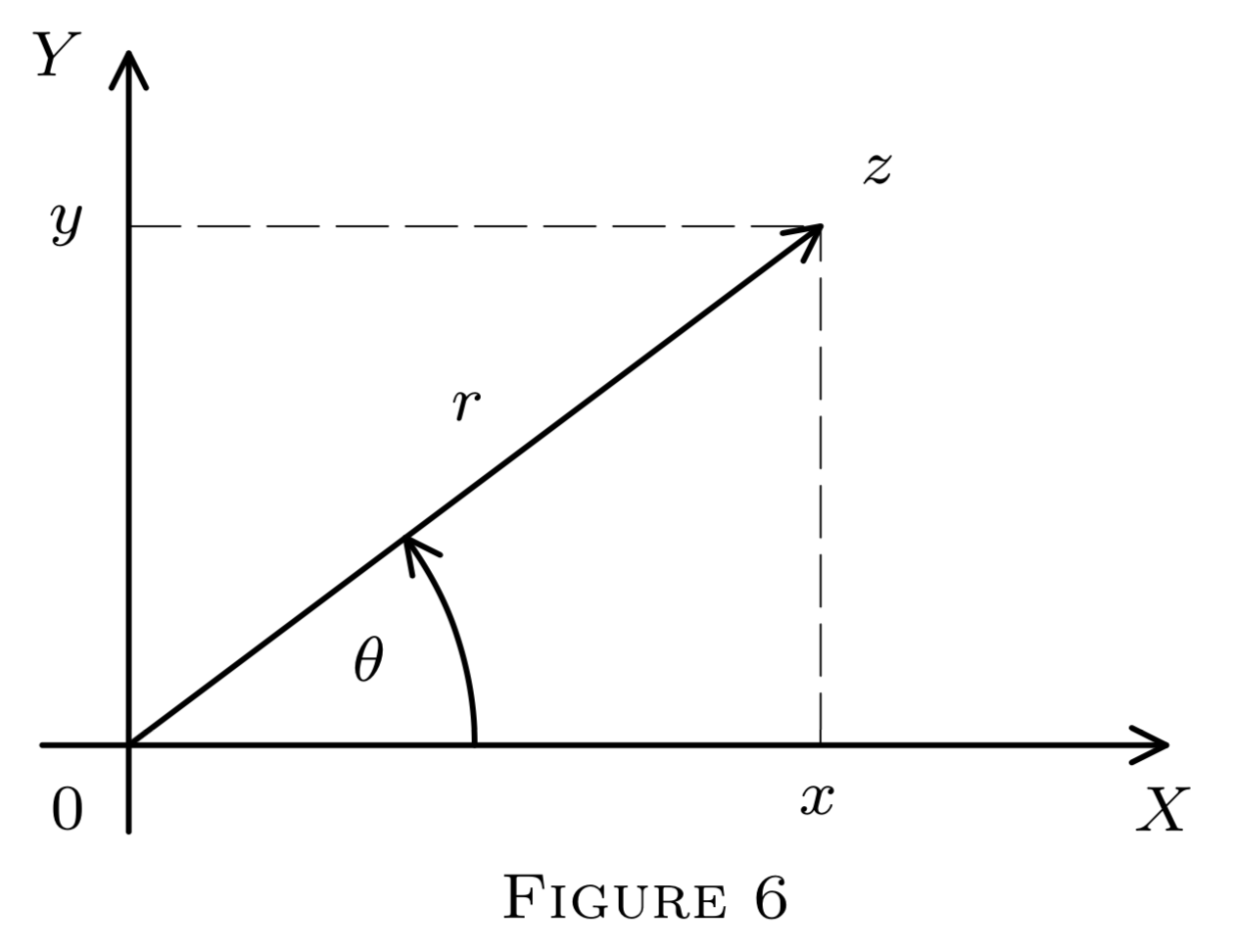
\[z=r(\cos \theta+i \sin \theta)(\text{trigonometric or polar form of }z).\]