1.9: La función arg (z)
- Page ID
- 109923
Funciones de muchos a uno
La función se\(f(z) = z^2\) mapea\(\pm z\) al mismo valor, e.g\(f(2) = f(-2) = 4\). Decimos que\(f(z)\) es una función de 2 a 1. Es decir, mapea 2 puntos diferentes a cada valor. (Técnicamente, solo mapea un punto a 0, pero por ahora pasaremos por alto eso). Aquí hay algunos otros ejemplos de funciones de muchos a uno.
\(w = z^3\)es una función de 3 a 1. Por ejemplo, 3\(z\) valores diferentes se mapean a\(w = 1\):
\(1^3 = (\dfrac{-1 + \sqrt{3} i}{2})^3 = (\dfrac{-1 - \sqrt{3} i}{2})^3 = 1\)
La función\(w = e^z\) mapea infinitamente muchos puntos a cada valor. Por ejemplo
\(e^0 = e^{2\pi i} = e^{4\pi i} = ... = e^{2n \pi i} = ... = 1\)
\(e^{i \pi /2} = e^{i \pi /2 + 2\pi i} = e^{i \pi /2 + 4 \pi i} = ... = e^{i\pi /2 + 2 n \pi i} = ... = 1\)
En general,\(e^{z + 2n \pi i}\) tiene el mismo valor para cada entero\(n\).
Sucursales de\(\text{arg} (z)\)
Debes dominar esta sección. Las ramas de\(\text{arg} (z)\) son la clave que realmente subyace a todos nuestros otros ejemplos. Afortunadamente es razonablemente sencillo.
El punto clave es que el argumento sólo se define hasta múltiplos de\(2\pi i\) por lo que cada\(z\) produce infinitamente muchos valores para\(\text{arg} (z)\). Debido a esto diremos que\(\text{arg} (z)\) es una función de múltiples valores.
En general una función debe tomar solo un valor. Lo que eso significa en la práctica es que cada vez que usemos tal función habrá que tener cuidado para especificar a cuál de los posibles valores nos referimos. Esto se conoce como especificar una rama de la función.
Por una rama de la función de argumento nos referimos a una elección de rango para que se convierta en un solo valor. Al especificar una rama estamos diciendo que tomaremos el valor único de\(\text{arg} (z)\) que se encuentra en la rama.
Veamos varias ramas diferentes para entender cómo funcionan:
(i). Si especificamos la rama como\(0 \le \text{arg} (z) < 2\pi\) entonces tenemos los siguientes argumentos.
\(\text{arg} (1) = 0\);\(\text{arg} (i) = \pi /2\);\(\text{arg} (-1) = \pi \);\(\text{arg} (-i) = 3 \pi /2\)
Esta rama y estos puntos se muestran gráficamente en la Figura (i) a continuación.
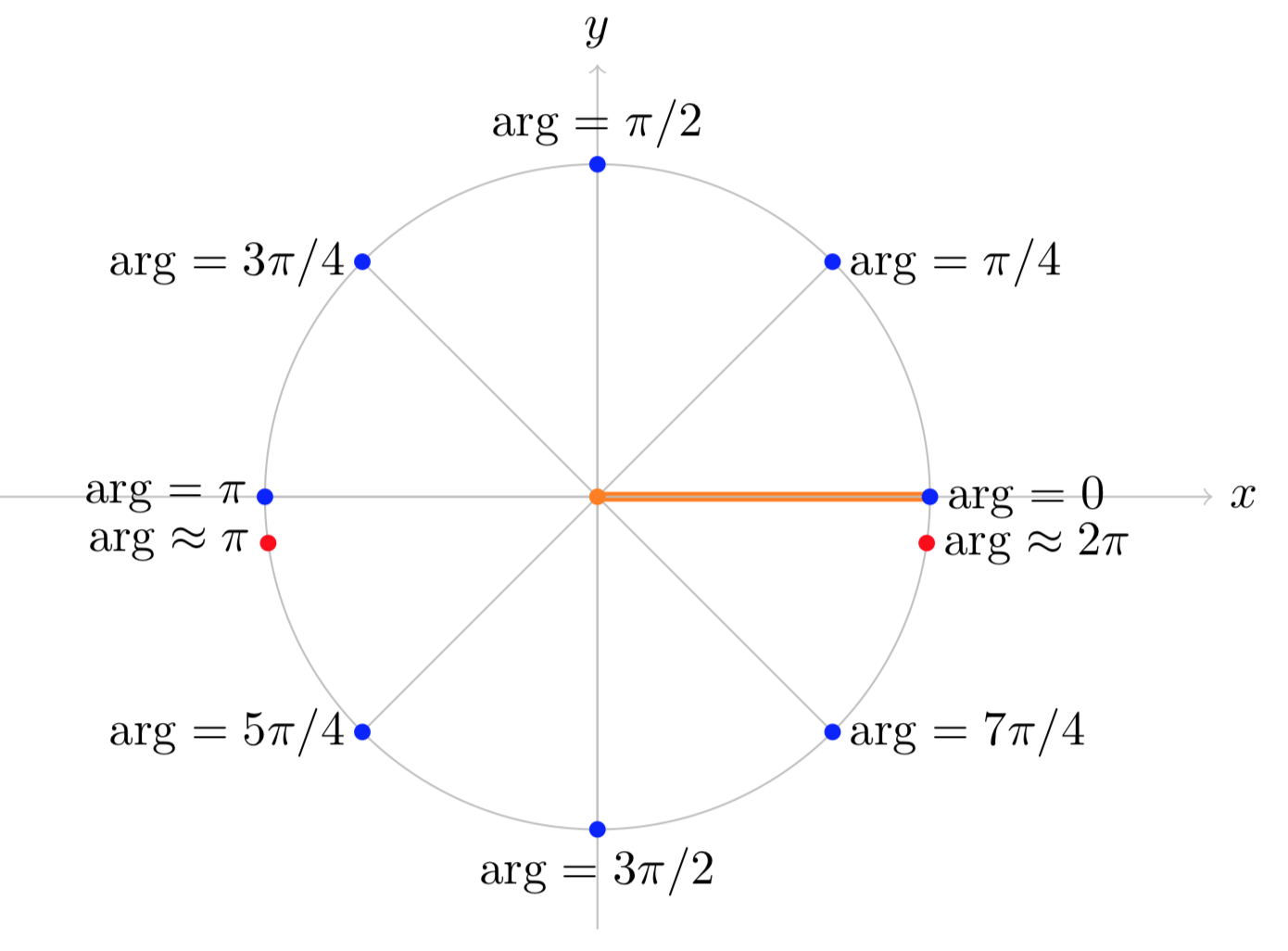
Figura (i): La rama\(0 \le \text{arg} (z) < 2\pi\) de\ text {arg} (z)\).
Observe que si empezamos en\(z = 1\) sobre el eje real positivo tenemos\(\text{arg} (z) = 0\). Luego\(\text{arg} (z)\) aumenta a medida que nos movemos en sentido antihorario alrededor del círculo. El argumento es continuo hasta que volvemos al eje real positivo. Ahí salta de casi\(2 \pi\) atrás a 0.
No hay forma de moverse (sin juego de palabras intencionado) esta discontinuidad. Si necesitamos\(\text{arg} (z)\) ser continuos tendremos que eliminar (cortar) los puntos de discontinuidad fuera del dominio. El corte de rama para esta rama de\(\text{arg} (z)\) se muestra como una gruesa línea naranja en la figura. Si hacemos el corte de rama entonces el dominio para\(\text{arg} (z)\) es el plano menos el corte, es decir, solo consideraremos\(\text{arg} (z)\) para\(z\) no en el corte.
Para futuras referencias hay que señalar que, en esta rama,\(\text{arg} (z)\) es continuo cerca del eje real negativo, es decir, los argumentos de los puntos cercanos están cerca unos de otros.
ii). Si especificamos la rama como\(-\pi < \text{arg} (z) \le \pi\) entonces tenemos los siguientes argumentos:
\(\text{arg} (1) = 0\);\(\text{arg} (i) = \pi /2\);\(\text{arg} (-1) = \pi\);\(\text{arg} (-i) = -\pi /2\)
Esta rama y estos puntos se muestran gráficamente en la Figura (ii) a continuación.
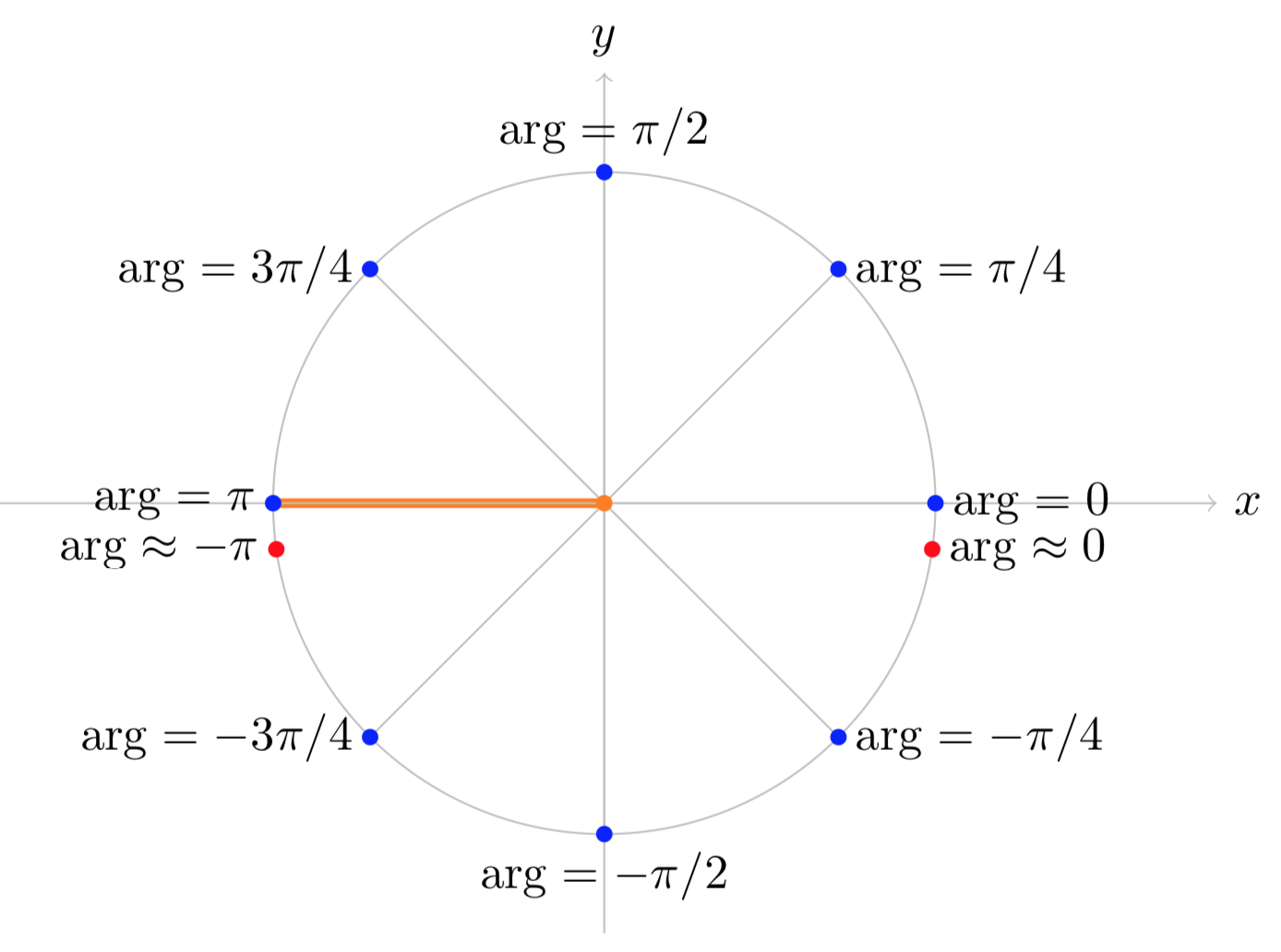
Figura (ii): La rama\(-\pi < \text{arg} (z) \le \pi\) de\(\text{arg} (z)\).
Compare la Figura (ii) con la Figura (i). Los valores de\(\text{arg} (z)\) son los mismos en el plano de la mitad superior, pero en el plano de la mitad inferior difieren en\(2 \pi\).
Para esta rama el corte de rama es a lo largo del eje real negativo. Al cruzar la rama cortamos el valor de los\(\text{arg} (z)\) saltos de\(\pi\) a algo cercano a\(-\pi\).
iii). La figura (iii) muestra la rama de\(\text{arg} (z)\) con\(\pi /4 \le \text{arg} (z) < 9 \pi /4\).
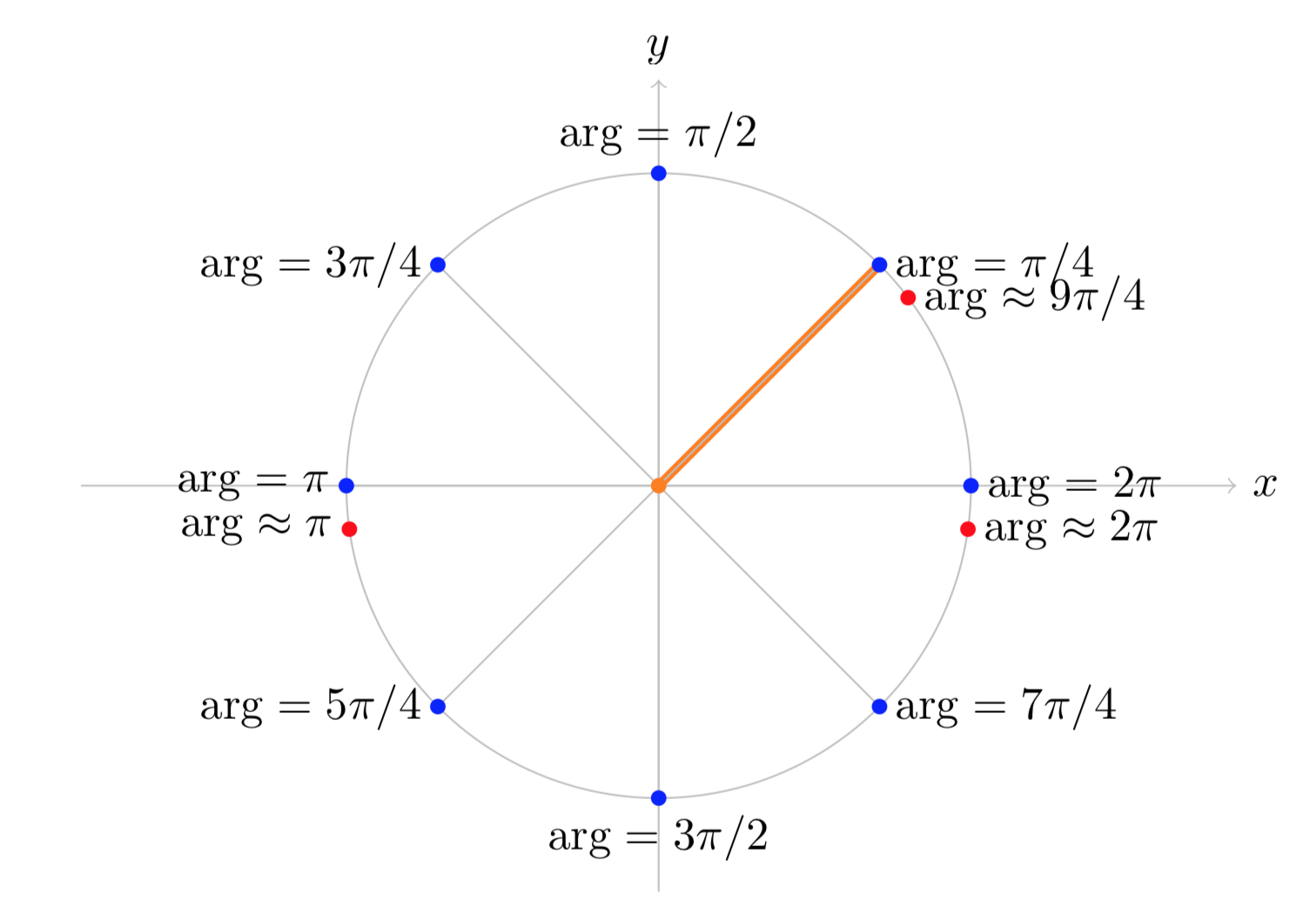
Figura (iii): La rama\(\pi /4 \le \text{arg} (z) < 9 \pi /4\) de\(\text{arg} (z)\).
Observe que en esta rama\(\text{arg} (z)\) es continuo tanto en el eje real positivo como en el negativo. El salto de\(2\pi \) ocurre a lo largo del rayo en ángulo\(\pi /4\).
iv). Obviamente, hay muchas muchas sucursales posibles. Por ejemplo,
\(42 < \text{arg} (z) \le 42 + 2\pi \).
(v). No vamos a hacer uso de esto en 18.04, pero, de hecho, el corte de rama no tiene que ser una línea recta. Cualquier curva que vaya desde el origen hasta el infinito servirá. El argumento será continuo a excepción de un salto por\(2 \pi\) cuando\(z\) cruza el corte de rama.
rama principal de\(\text{arg} (z)\)
Se destaca la rama (ii) en el apartado anterior y se le da nombre:
A la sucursal\(-\pi < \text{arg} (z) \le \pi\) se le llama la rama principal de\(\text{arg} (z)\). Usaremos la notación\(\text{Arg} (z)\) (A mayúscula) para indicar que estamos usando la rama principal. (Por supuesto, en los casos en que no queramos que haya ninguna duda vamos a decir explícitamente que estamos usando la rama principal.)
Continuidad de\(\text{arg} (z)\)
Los ejemplos anteriores muestran que no hay forma de moverse por el salto de\(2 \pi\) mientras cruzamos el corte de rama. Esto quiere decir que cuando necesitamos\(\text{arg} (z)\) ser continuos tendremos que restringir su dominio al plano menos un corte de rama.


