5.5: Sorprendente consecuencia de la fórmula integral de Cauchy
- Page ID
- 109841
Existencia de derivados
Supongamos que\(f(z)\) es analítico en una región\(A\). Entonces,\(f\) tiene derivados de todo orden.
- Prueba
-
Esto se desprende de la fórmula integral de Cauchy para derivados. Es decir, tenemos una fórmula para todos los derivados, por lo que en particular los derivados existen todos.
Un poco más precisamente: para cualquier punto\(z\) en\(A\) podemos poner alrededor un pequeño disco\(z_0\) que esté completamente contenido en\(A\). \(C\)Sea el límite del disco, entonces la fórmula de Cauchy da una fórmula para todas las derivadas\(f^{(n)} (z_0)\) en términos de integrales sobre\(C\). En particular, esos derivados existen.
Observación. Si miras la prueba de la fórmula de Cauchy para derivados verás que\(f\) tener derivados de todos los pedidos se reduce a\(1/(w - z)\) tener derivados de todos los pedidos para\(w\) en una curva que no contiene\(z\).
Observación importante. A veces hemos asumido que para\(f(u + iv)\) analítica,\(u\) y\(v\) tienen derivadas parciales continuas de orden superior. Este teorema confirma ese hecho. En particular\(u_{xy} = u_{yx}\),, etc.
Desigualdad de Cauchy
\(C_R\)Déjese ser el círculo\(|z - z_0| = R\). Supongamos que\(f(z)\) es analítico en\(C_R\) y su interior, es decir, en el disco\(|z - z_0| \le R\). Finalmente\(M_R = \text{max } |f(z)|\) déjalo\(z\) pasar\(C_R\). Entonces
\[|f^{(n)} (z_0)| \le \dfrac{n! M_R}{R^n}, \ \ \ n = 1, 2, 3, ...\]
- Prueba
-
Usando la fórmula integral de Cauchy para derivados (Ecuación 5.3.1) tenemos
\[|f^{(n)} (z_0)| \le \dfrac{n!}{2\pi} \int_{C_R} \dfrac{|f(w)|}{|w - z_0|^{n + 1}} |dw| \le \dfrac{n!}{2\pi} \dfrac{M_R}{R^{n + 1}} \int_{C_R} |dw| = \dfrac{n!}{2\pi} \dfrac{M_R}{R^{n + 1}} \int_{C_R} \cdot 2\pi R\]
Teorema de Liouville
Supongamos que\(f(z)\) es entero y supongamos que está acotado en el plano complejo, es decir,\(|f(z)| < M\) para todos\(z \in C\) entonces\(f(z)\) es constante.
- Prueba
-
Para cualquier círculo de radio\(R\) alrededor de\(z_0\) la desigualdad de Cauchy dice\(|f'(z_0)| \le \dfrac{M}{R}\). Pero,\(R\) puede ser tan grande como nos guste así que concluimos que\(|f'(z_0)| = 0\) para cada uno\(z_0 \in C\). Dado que la derivada es 0, la función en sí es constante.
En resumen:
Si\(f\) es entero y acotado entonces\(f\) es constante.
Ahora, prácticamente gratis, obtenemos el teorema fundamental del álgebra.\(P(z) = a_n z^n + ... + a_0\),\(\sin (z)\),\(e^z\) son todos enteros pero no acotados.
Cualquier polinomio\(P\) de grado\(n \ge 1\), i.e.
\[P(z) = a_0 + a_1 z + ... + a_n z^n, a_n \ne 0,\]
tiene exactamente\(n\) raíces.
- Prueba
-
Hay dos partes a la prueba.
Parte dura: Mostrar que\(P\) tiene al menos una raíz.
Esto se hace por contradicción, junto con el teorema de Liouville. Supongamos que\(P(z)\) no tiene un cero. Entonces
- \(f(z) = 1/P(z)\)es entero. Esto es obvio porque (por supuesto) no\(P(z)\) tiene ceros.
- \(f(z)\)está acotado. Esto sigue porque\(1/P(z)\) va a 0 como\(|z|\) va a\(\infty\).
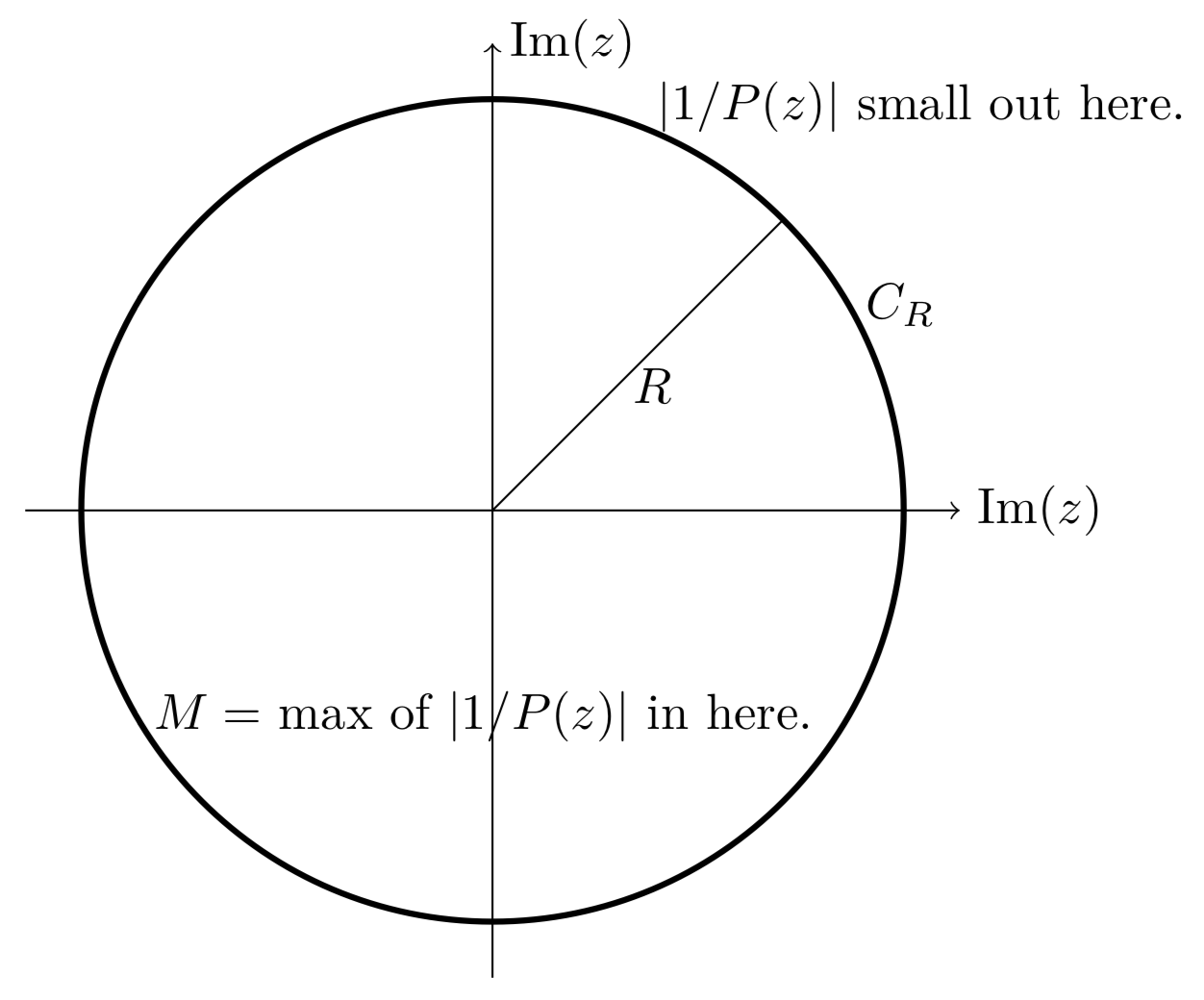
(Está claro que\(|1/P(z)|\) va a 0 como\(z\) va al infinito, es decir,\(|1/P(z)|\) es pequeño fuera de un círculo grande. Así\(|1/P(z)|\) está delimitado por\(M\).)
Entonces, por el teorema de Liouville\(f(z)\) es constante, y por lo tanto\(P(z)\) debe ser constante también. Pero esto es una contradicción, por lo que la hipótesis de “No ceros” debe estar equivocada, es decir,\(P\) debe tener un cero.
Parte fácil:\(P\) tiene exactamente\(n\) ceros. \(z_0\)Sea uno cero. Podemos factorizar\(P(z) = (z - z_0) Q(z)\). \(Q(z)\)tiene título\(n - 1\). Si\(n -1 > 0\), entonces podemos aplicar el resultado a\(Q(z)\). Podemos continuar con este proceso hasta que el grado de\(Q\) sea 0.
Principio de módulo máximo
Brevemente, el principio de módulo máximo establece que si\(f\) es analítico y no constante en un dominio\(A\) entonces no\(|f(z)|\) tiene máximo relativo en\(A\) y el máximo absoluto de\(|f|\) ocurre en el límite de\(A\).
Para probar el principio de módulo máximo primero probaremos la propiedad de valor medio. Esto te dará una buena sensación para el principio de módulo máximo. También es importante e interesante por derecho propio.
Supongamos que\(f(z)\) es analítico en el disco cerrado de radio\(r\) centrado en\(z_0\), es decir, el conjunto\(|z - z_0| \le r\). Entonces,
\[f(z_0) = \dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta})\ d \theta\]
- Prueba
-
Esta es una aplicación de la fórmula integral de Cauchy en el disco\(D_r = |z - z_0| \le r\).
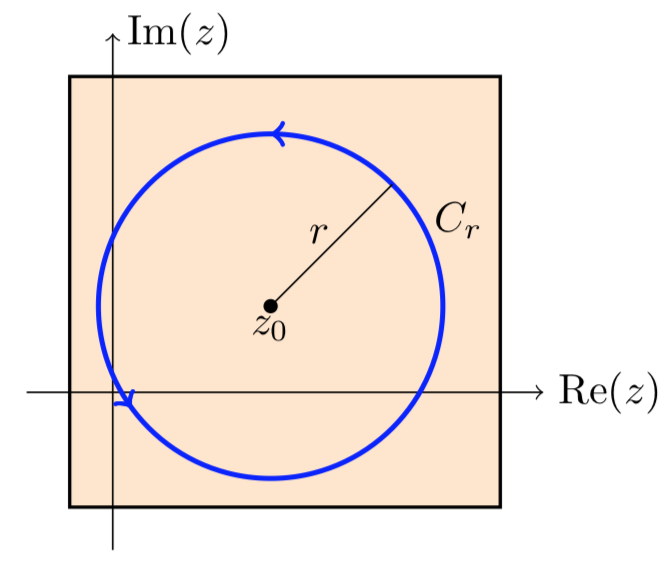
Podemos parametrizar\(C_r\), el límite de\(D_r\), como
\[\gamma (\theta) = z_0 + re^{i \theta}, \text{ with } 0 \le \theta \le 2\pi, \text{ so } \gamma ' (\theta) = ire^{i \theta}.\]
Por la fórmula de Cauchy tenemos
\[f(z_0) = \dfrac{1}{2\pi i} \int_{C_r} \dfrac{f(z)}{z - z_0}\ dz = \dfrac{1}{2\pi i} \int_{0}^{2\pi} \dfrac{f(z_0 + re^{i\theta})}{re^{i \theta}} ire^{i \theta} \ d \theta = \dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta}) \ d\theta\]
Esto prueba el inmueble.
En palabras, la propiedad de valor medio dice\(f(z_0)\) es la media aritmética de los valores en el círculo. Ahora podemos afirmar y probar el principio de módulo máximo. Nosotros exponemos cuidadosamente los supuestos.
Al aplicar este teorema, es importante verificar que los supuestos están satisfechos.
Supongamos que\(f(z)\) es analítico en una región conectada\(A\) y\(z_0\) es un punto en\(A\).
- Si\(|f|\) tiene un máximo relativo en\(z_0\) entonces\(f(z)\) es constante en un vecindario de\(z_0\).
- Si\(A\) está delimitado y conectado, y\(f\) es continuo en\(A\) y su límite, entonces o bien\(f\) es constante o el máximo absoluto de\(|f|\) ocurre solo en el límite de\(A\).
- Prueba
-
Parte (1): El argumento para la parte (1) es un poco quisquilloso. Utilizaremos la propiedad de valor medio y la desigualdad del triángulo del Teorema 5.3.2.
Ya que\(z_0\) es un máximo relativo de\(|f|\), por cada círculo lo suficientemente pequeño\(C\):\(|z - z_0| = r\) alrededor\(z_0\) tenemos\(|f(z)| \le |f(z_0)|\) para\(z\) en\(C\). Por lo tanto, por la propiedad de valor medio y la desigualdad del triángulo
\[\begin{array} {rclcc} {|f(z_0)|} & = & {|\dfrac{1}{2\pi} \int_{0}^{2\pi} f(z_0 + re^{i \theta}) \ d \theta|} & \ \ \ & {\text{(mean value property)}} \\ {} & \le & {\dfrac{1}{2\pi} \int_{0}^{2\pi} |f(z_0 + re^{i \theta})| \ d \theta} & \ \ \ & {\text{(triangle inequality)}} \\ {} & \le & {\dfrac{1}{2\pi} \int_{0}^{2\pi} |f(z_0)|\ d\theta} & \ \ \ & {(|f(z_0 + re^{i \theta}| \le |f(z_0)|)} \\ {} & = & {|f(z_0)|} & \ \ \ & {} \end{array}\]
Desde el principio y el final de lo anterior son ambos\(|f(z_0)|\) todas las desigualdades en la cadena deben ser igualdades.
La primera desigualdad sólo puede ser una igualdad si para todos\(\theta\), se\(f(z_0 + re^{i\theta})\) encuentran en el mismo rayo desde el origen, es decir, tienen el mismo argumento o son 0.
La segunda desigualdad sólo puede ser una igualdad si todos\(|f(z_0 + re^{i \theta})| = |f(z_0)|\). Entonces todos\(f(z_0 + re^{i \theta})\) tenemos la misma magnitud y la misma argumenía. Esto implica que todos son iguales.
Finalmente, si\(f(z)\) es constante a lo largo del círculo y\(f(z_0)\) es el promedio de\(f(z)\) sobre el círculo entonces\(f(z) = f(z_0)\)\), es decir,\(f\) es constante en un pequeño disco alrededor\(z_0\).
Parte (2): Los supuestos que\(A\) está delimitado y\(f\) es continuo\(A\) y su límite sirven para garantizar que\(|f|\) tiene un máximo absoluto (en\(A\) combinado con su límite). La parte (1) garantiza que el máximo absoluto no puede estar en el interior de la región\(A\) a menos que\(f\) sea constante. (Esto requiere un poco más de argumento. ¿Ves por qué?) Si el máximo absoluto no está en el interior debe estar en el límite.
Encuentra el módulo máximo de\(e^z\) en la unidad cuadrada con\(0 \le x, y \le 1\).
Solución
\[|e^{x + iy}| = e^x,\]
por lo que el máximo es cuando\(x = 1\),\(0 \le y \le 1\) es arbitrario. Esto es, de hecho, en el límite de la plaza de la unidad
Encuentra el módulo máximo para\(\sin (z)\) en el cuadrado\([0, 2\pi] \times [0, 2\pi]\).
Solución
Utilizamos la fórmula
\[\sin (z) = \sin x \cosh y + i \cos x \sinh y.\]
Entonces,
\[\begin{array} {rcl} {|\sin (z)|^2} & = & {\sin ^2 x \cosh ^2 y + \cos ^2 x \sinh ^2 y} \\ {} & = & {\sin ^2 x \cosh ^2 y + (1 - \sin ^2 x) \sinh ^2 y} \\ {} & = & {\sin ^2 x + \sinh ^2 y} \end{array}\]
Sabemos que el máximo sobre\(x\) de\(\sin ^2 (x)\) es en\(x = \pi /2\) y\(x = 3\pi /2\). El máximo de\(\sinh ^2 y\) es en\(y = 2\pi\). Entonces el módulo máximo es
\[\sqrt{1 + \sinh ^2 (2\pi)} = \sqrt{\cosh ^2 (2\pi)} = \cosh (2\pi).\]
Esto ocurre en los puntos
\[z = x + iy = \dfrac{\pi}{2} + 2\pi i, \text{ and } z = \dfrac{3\pi}{2} + 2\pi i.\]
Ambos puntos se encuentran en el límite de la región.
Supongamos que\(f(z)\) es entero. Demuéstralo si\(\lim_{z \to \infty} f(z) = 0\) entonces\(f(z) \equiv 0\).
Solución
Este es un uso estándar del principio de módulo máximo. La estrategia es mostrar que el máximo de no\(|f(z)|\) está en el límite (de la región elegida apropiadamente), por lo que\(f(z)\) debe ser constante.
Arreglar\(z_0\). Para\(R > |z_0|\) dejar\(M_R\) ser el máximo de\(|f(z)|\) en el círculo\(|z| = R\). El teorema del módulo máximo dice eso\(|f(z_0)| < M_R\). Ya que\(f(z)\) va a 0, como\(R\) va al infinito, debemos tener\(M_R\) también va a 0. Esto significa\(|f(z_0)| = 0\). Ya que esto es cierto para cualquiera\(z_0\), tenemos\(f(z) \equiv 0\).
Aquí hay un ejemplo de por qué necesitas\(A\) estar acotado en el teorema del módulo máximo. Dejar\(A\) ser el medio plano superior
\[\text{Im} (z) > 0.\]
Entonces el límite de\(A\) es el eje real.
Vamos\(f(z) = e^{-iz}\). Tenemos
\[|f(x)| = |e^{-ix}| = 1\]
para\(x\) a lo largo del eje real. Ya que\(|f(2i)| = |e^2| > 1\), vemos\(|f|\) no puede tomar su máximo a lo largo del límite de\(A\).
Por supuesto, no puede tomar su máximo en el interior de\(A\) ninguno de los dos. Lo que pasa aquí es que\(f(z)\) no tiene un módulo máximo. Efectivamente\(|f(z)|\) va al infinito a lo largo del eje imaginario positivo.


