1.1: Funciones
- Page ID
- 110581
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)¿Qué es una función?
El mundo natural está lleno de relaciones entre cantidades que cambian. Cuando vemos estas relaciones, es natural que preguntemos Si conozco una cantidad, ¿puedo entonces determinar la otra?
Esto establece la idea de una cantidad de entrada, o variable independiente, y una cantidad de salida correspondiente, o variable dependiente. De esto obtenemos la noción de una relación funcional en la que la salida se puede determinar a partir de la entrada.
Para algunas cantidades, como la altura y la edad, ciertamente existen relaciones entre estas cantidades. Dada una persona específica y cualquier edad, es bastante fácil determinar su estatura, pero si intentamos revertir esa relación y determinar la altura a partir de una edad determinada, eso sería problemático, ya que la mayoría de las personas mantienen la misma altura durante muchos años.
Una función es una regla para una relación entre una cantidad de entrada, o independiente, y una cantidad de salida, o dependiente, en la que cada valor de entrada determina de manera única un valor de salida. Decimos que la salida es una función de la entrada.
En el ejemplo de altura y edad anterior, ¿la estatura es función de la edad? ¿La edad es una función de la altura?
Solución
En el ejemplo de altura y edad anterior, sería correcto decir que la altura es una función de la edad, ya que cada edad determina de manera única una altura. Por ejemplo, en mi 18 cumpleaños, tenía exactamente una altura de 69 pulgadas.
Sin embargo, la edad no es función de la altura, ya que una entrada de altura podría corresponder con más de una edad de salida. Por ejemplo, para una altura de entrada de 70 pulgadas, hay más de una salida de edad ya que tenía 70 pulgadas a la edad de 20 y 21 años.
Notación de funciones
Para simplificar la escritura de expresiones y ecuaciones que involucran funciones, a menudo se usa una notación simplificada. También utilizamos variables descriptivas para ayudarnos a recordar el significado de las cantidades en el problema.
En lugar de escribir la altura es una función de la edad,
podríamos usar la variable descriptiva\(h\) para representar la altura y podríamos usar la variable descriptiva\(a\) para representar la edad.
| “la altura es una función de la edad” | si nombramos la función\(f\) escribimos |
| “\(h\)es\(f\) de\(a\)” | o más simplemente |
| \(h = f(a)\) | podríamos nombrar la función\(h\) y escribir |
| \(h(a)\) | que se lee "\(h\)de\(a\)” |
Recuerda que podemos usar cualquier variable para nombrar la función; la notación nos\(h(a)\) muestra que\(h\) depende de\(a\). El valor \(a\)
debe ser puesto en la función \(h\)
para obtener un resultado. Ten cuidado — los paréntesis indican que la edad se introduce en la función (Nota: ¡no confundas estos paréntesis con multiplicación!).
La salida de notación =\(f\) (entrada) define una función llamada\(f\). Esta sería la salida leída es\(f\) de entrada.
Una función\(N = f(y)\) da el número de policías,\(N\), en una localidad en año\(y\). ¿Qué\(f(2005) = 300\) nos dice?
Solución
Cuando leemos\(f(2005) = 300\), vemos que la cantidad de entrada es 2005, que es un valor para la cantidad de entrada de la función, el año (\(y\)). El valor de salida es 300, el número de policías (\(N\)), un valor para la cantidad de salida. Recuerda\(N=f(y)\). Entonces esto nos dice que en el año 2005 había 300 policías en la localidad.
Tablas como funciones
Las funciones se pueden representar de muchas maneras: Palabras (como hicimos en los últimos ejemplos), tablas de valores, gráficas o fórmulas. Representados como una tabla, se nos presenta una lista de valores de entrada y salida.
Esta tabla representa la edad de los niños en años y sus alturas correspondientes. Si bien algunas tablas muestran toda la información que conocemos sobre una función, esta tabla en particular representa solo algunos de los datos disponibles para la altura y las edades de los niños.
| (entrada)\(a\), edad en años | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|
| (salida)\(h\), altura en pulgadas | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
¿Cuál de estas tablas define una función (si la hay)?
| Entrada | Salida |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Entrada | Salida |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Entrada | Salida |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Solución
Las tablas primera y segunda definen funciones. En ambos, cada entrada corresponde exactamente a una salida. La tercera tabla no define una función ya que el valor de entrada de 5 corresponde con dos valores de salida diferentes.
Resolver y evaluar funciones
Cuando trabajamos con funciones, hay dos cosas típicas que hacemos: evaluar y resolver. Evaluar una función es lo que hacemos cuando conocemos una entrada, y usamos la función para determinar la salida correspondiente. Evaluar siempre producirá un resultado, ya que cada entrada de una función corresponde exactamente a una salida.
Resolver ecuaciones que involucran una función es lo que hacemos cuando conocemos una salida, y usamos la función para determinar las entradas que producirían esa salida. Resolver una función podría producir más de una solución, ya que diferentes entradas pueden producir la misma salida.
Usando la tabla que se muestra, donde\(Q=g(n)\)
| \(n\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| \(Q\) | 8 | 6 | 7 | 6 | 8 |
- Evaluar\(g(3)\)
- Resolver\(g(n)=6\)
Solución
- Evaluar\(g(3)\): Evaluar\(g(3)\) (léase:
g de 3
) significa que necesitamos determinar el valor de salida,\(Q\), de la función g dado el valor de entrada de\(n=3\). Al mirar la tabla, vemos la salida correspondiente a\(n=3\) is\(Q=7\), permitiéndonos concluir\(g(3) = 7\). - Resolver\(g(n)=6\): Resolver\(g(n) = 6\) significa que necesitamos determinar qué valores de entrada\(n\),, producir un valor de salida de 6. Al mirar la mesa vemos que hay dos soluciones:\(n = 2\) y\(n = 4\). Cuando ingresamos 2 en la función\(g\), nuestra salida es\(Q = 6\). Cuando ingresamos 4 en la función\(g\), nuestra salida también lo es\(Q = 6\).
Gráficas como funciones
A menudo se puede utilizar una gráfica de una relación para definir una función. Por convención, los gráficos se crean típicamente con la cantidad de entrada a lo largo del eje horizontal y la cantidad de salida a lo largo de la vertical.
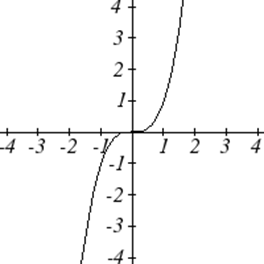
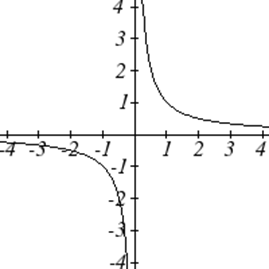
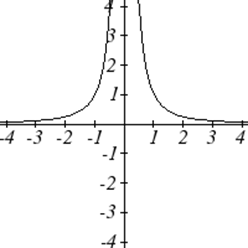
¿Cuál de estas gráficas define una función\(y=f(x)\)?
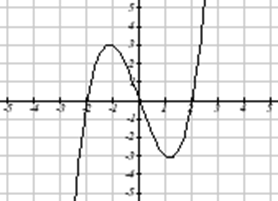
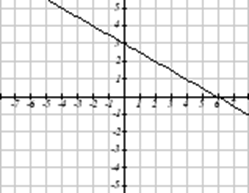
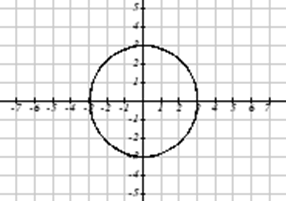
Solución
Al observar las tres gráficas anteriores, las dos primeras definen una función\(y=f(x)\), ya que para cada valor de entrada a lo largo del eje horizontal hay exactamente un valor de salida correspondiente, determinado por el valor y de la gráfica. La tercera gráfica no define una función\(y=f(x)\) ya que algunos valores de entrada, como\(x=2\), corresponden con más de un valor de salida.
La prueba de línea vertical es una manera práctica de pensar si un gráfico define la salida vertical como una función de la entrada horizontal. Imagina dibujar líneas verticales a través de la gráfica. Si alguna línea vertical cruzaría la gráfica más de una vez, entonces la gráfica no define solo una salida vertical para cada entrada horizontal.
Evaluar una función usando una gráfica requiere tomar la entrada dada y usar la gráfica para buscar la salida correspondiente. Resolver una ecuación de función usando una gráfica requiere tomar la salida dada y mirar en la gráfica para determinar la entrada correspondiente.
Teniendo en cuenta la siguiente gráfica,
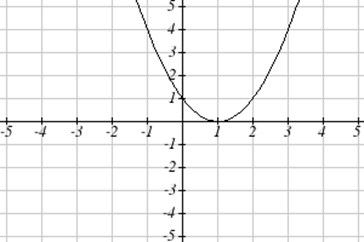
- Evaluar\(f(2)\).
- Resolver\(f(x) = 4\).
Solución
- Para evaluar\(f(2)\), encontramos la entrada de\(x=2\) en el eje horizontal. Al subir a la gráfica se da el punto (2, 1), dando una salida de\(y=1\). Entonces\(f(2) = 1\).
- Para resolver\(f(x) = 4\), encontramos el valor 4 en el eje vertical porque si\(f(x) = 4\) entonces 4 es la salida. Al moverse horizontalmente a través de la gráfica se obtienen dos puntos con la salida de 4: (-1,4) y (3,4). Estos dan las dos soluciones a\(f(x) = 4\):\(x = -1\) o\(x = 3\). Esto significa\(f(-1)=4\) y\(f(3)=4\), o cuando la entrada es -1 o 3, la salida es 4.
Observe que si bien la gráfica en el ejemplo anterior es una función, obtener dos valores de entrada para el valor de salida de 4 nos muestra que esta función no es uno a uno.
Fórmulas como funciones
Cuando es posible, es muy conveniente definir relaciones usando fórmulas. Si es posible expresar la salida como una fórmula que involucra la cantidad de entrada, entonces podemos definir una función.
Expresar la relación\(2n + 6p = 12\) como una función\(p = f(n)\) si es posible.
Solución
Para expresar la relación en esta forma, necesitamos poder escribir la relación donde\(p\) es una función de\(n\), lo que significa escribirla como\(p =\) [algo que implica\(n\)].
| \(2n + 6p = 12\) | restar\(2n\) de ambos lados |
| \(6p = 12 - 2n\) | dividir ambos lados por 6 y simplificar |
\[p=\frac{12-2n}{6}=\frac{12}{6}-\frac{2n}{6}=2-\frac{1}{3}n\nonumber \]
Habiendo reescrito la fórmula como\(p=\), ahora podemos expresar\(p\) como una función:\(p=f(n)=2-\frac{1}{3}n\)
No todas las relaciones pueden expresarse como una función con una fórmula.
Al igual que con las tablas y gráficas, es común evaluar y resolver funciones que involucran fórmulas. Evaluar requerirá reemplazar la variable de entrada en la fórmula con el valor proporcionado y calcular. Resolver requerirá reemplazar la variable de salida en la fórmula con el valor proporcionado, y resolver la (s) entrada (s) que produciría esa salida.
Dada la función\(k(t)=t^3+2\):
- Evaluar\(k(2)\).
- Resolver\(k(t)=1\).
Solución
- Para evaluar\(k(2)\), conectamos el valor de entrada 2 en la fórmula dondequiera que veamos la variable de entrada\(t\), luego simplificamos:\[\begin{align*}k(2) & = 2^3+2\\k(2) & = 8+2 \end{align*}\nonumber \] Entonces\(k(2) = 10\).
- Para resolver\(k(t) = 1\), establecemos la fórmula para\(k(t)\) igual a 1, y resolvemos para el valor de entrada que producirá esa salida:\[\begin{align*} k(t) & = 1 & \\ t^3+2 & = 1 &\text{substitute the original formula} \\ t^3 & = -1 &\text{subtract 2 from each side} \\ t & = 1 &\text{take the cube root of each side} \end{align*}\nonumber \]
Al resolver una ecuación usando fórmulas, puedes verificar tu respuesta usando tu solución en la ecuación original para ver si tu respuesta calculada es correcta.
Queremos saber si\(k(t) = 1\) es cierto cuándo\(t=-1\):\[\begin{align*}k(-1) & = (-1)^3+2\\ & = -1+2\\ & = 1,\end{align*}\nonumber \] cual fue el resultado deseado.
Funciones básicas del kit de herramientas
Hay algunas funciones básicas de las que es útil conocer el nombre y la forma de. A estos los llamamos el kit de herramientas básico de funciones.
Para estas definiciones usaremos\(x\) como la variable de entrada y\(f(x)\) como la variable de salida.
| Lineal | |
| Constante: | \(f(x)=c\), donde\(c\) es una constante (número) |
| Identidad: | \(f(x)=x\) |
| Valor Absoluto: | \(f(x)=|x|\) |
| Poder | |
| Cuadrática: | \(f(x)=x^2\) |
| Cúbico: | \(f(x)=x^3\) |
| Recíproco: | \(f(x)=\frac{1}{x}\) |
| Recíproco al cuadrado: | \(f(x)=\frac{1}{x^2}\) |
| Raíz cuadrada: | \(f(x)=\sqrt[2]{x}=\sqrt{x}\) |
| Raíz cúbica: | \(f(x)=\sqrt[3]{x}\) |
Gráficas de las Funciones del Toolkit
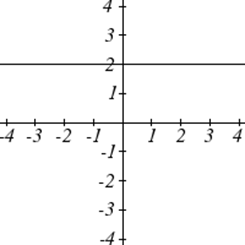
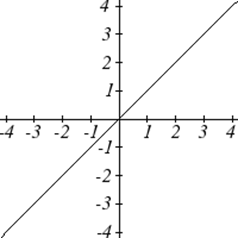
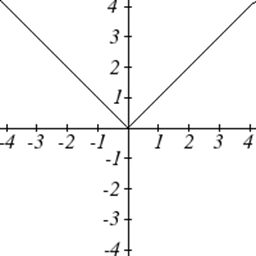
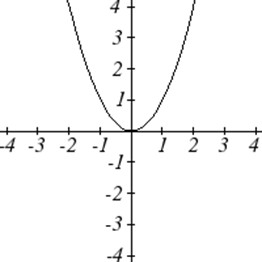
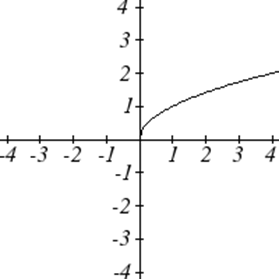
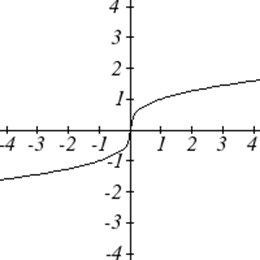
Uno de nuestros principales objetivos en matemáticas es modelar el mundo real con funciones matemáticas. Al hacerlo, es importante tener en cuenta las limitaciones de esos modelos que creamos.
Esta tabla muestra una relación entre la circunferencia y la altura de un árbol a medida que crece.
| Circunferencia,\(c\) | 1.7 | 2.5 | 5.5 | 8.2 | 13.7 |
| Altura,\(h\) | 24.5 | 31 | 45.2 | 54.6 | 92.1 |
Si bien existe una fuerte relación entre ambos, sin duda sería ridículo hablar de un árbol con una circunferencia de -3 pies, o una altura de 3000 pies. Cuando identificamos limitaciones en las entradas y salidas de una función, estamos determinando el dominio y el rango de la función.
- Dominio: El conjunto de posibles valores de entrada a una función.
- Rango: El conjunto de posibles valores de salida de una función
Usando la tabla de árbol anterior, determine un dominio y rango razonables.
Solución
Podríamos combinar los datos aportados con nuestras propias experiencias y razón para aproximar el dominio y rango de la función\( h = f(c)\). Para el dominio, posibles valores para la circunferencia de entrada c, no tiene sentido tener valores negativos, entonces\(c > 0\). Podríamos hacer una conjetura educada a un valor máximo razonable, o buscar que la circunferencia máxima medida sea de aproximadamente 119 pies. Con esta información diríamos que un dominio razonable es pies.
De manera similar para el rango, no tiene sentido tener alturas negativas, y la altura máxima de un árbol se podría mirar hacia arriba para ser 379 pies, por lo que un rango razonable son pies.
Una alternativa más compacta a la notación de desigualdad es la notación de intervalos, en la que los intervalos de valores son referidos por los valores inicial y final. Los paréntesis curvos se utilizan para estrictamente menos de,
y los corchetes se usan para menos de o igual a.
Como infinito no es un número, no podemos incluirlo en el intervalo, por lo que siempre usamos paréntesis curvos con\(\infty\) y\(-\infty\). La siguiente tabla te ayudará a ver cómo las desigualdades corresponden a la notación de intervalos:
| Desigualdad | Notación de intervalos |
|---|---|
| \( 5 \lt h \leq10 \) | (5, 10] |
| \(5\leq h \lt10 \) | [5, 10) |
| \(5 \lt h \lt 10\) | (5, 10) |
| \(h \lt10\) | \((-\infty,10)\) |
| \(h\geq10\) | \([10,\infty)\) |
| Todos los números reales (\(\mathbb{R}\)) | \((-\infty,\infty)\) |
Describa los intervalos de valores que se muestran en el gráfico de líneas a continuación usando el generador de conjuntos y las notaciones de intervalos

Solución
Para describir los valores,\(x\), que se encuentran en los intervalos mostrados anteriormente diríamos, \(x\)es un número real mayor o igual a 1 y menor o igual a 3, o un número real mayor que 5.
Como desigualdad es \(1\leq x\leq 3\)o\(x \gt 5 \)
. En notación de intervalos lo es \([1,3]\cup(5,\infty)\)
.
Encuentra el dominio de cada función:
- \(f(x)=2\sqrt{x+4}\)
- \(g(x)=\dfrac{3}{6-3x}\)
Solución
- Como no podemos tomar la raíz cuadrada de un número negativo, necesitamos que el interior de la raíz cuadrada sea no negativo. \(x+4\geq 0\)cuando\(x\geq -4\), entonces el dominio de\(f(x)\) es\([-4,\infty)\).
- No podemos dividir por cero, entonces necesitamos que el denominador sea distinto de cero. \(6-3x=0\)cuando\(x = 2\), por lo que debemos excluir 2 del dominio. El dominio de\(g(x)\) es\((-\infty,2)\cup(2,\infty)\).


