1.2: Operaciones en funciones

Composición de Funciones

Supongamos que queríamos calcular cuánto cuesta calentar una casa en un día determinado del año. El costo para calentar una casa dependerá de la temperatura media diaria, y la temperatura media diaria depende del día particular del año. Observe cómo acabamos de definir dos relaciones: La temperatura depende del día, y el costo depende de la temperatura. Usando variables descriptivas, podemos anotar estas dos funciones.

La primera función,$C(T)$, da el costo$C$ de calentar una casa cuando la temperatura media diaria es de$T$ grados centígrados, y la segunda$T(d)$,, da la temperatura media diaria de una ciudad en particular el día$d$ del año. Si quisiéramos determinar el costo de calentar la casa el quinto día del año, podríamos hacer esto uniendo nuestras dos funciones, una idea llamada composición de funciones. Usando la función$T(d)$, podríamos evaluar$T(5)$ para determinar la temperatura promedio diaria al quinto día del año. Entonces podríamos usar esa temperatura como entrada a la$C(T)$ función para encontrar el costo para calentar la casa el quinto día del año:$C(T(5))$.

Composición de Funciones

Cuando la salida de una función se usa como entrada de otra, llamamos a toda la operación una composición de funciones. Escribimos$f(g(x))$, y leemos esto como “$f$$g$de$x$” o “$f$compuesto con$g$ at$x$”.

Una notación alternativa para la composición utiliza el operador de composición:$\circ$. $(f\circ g)(x)$se lee “$f$$g$de$x$” o “$f$compuesto con$g$ at$x$”, al igual que$f(g(x))$.

Ejemplo$\PageIndex{1}$

Supongamos que$c(s)$ da la cantidad de calorías quemadas haciendo$s$ abdominales, y$s(t)$ da la cantidad de abdominales que una persona puede hacer en$t$ minutos. Interpretar$c(s(3))$.

Solución

Cuando se nos pide que interpretemos, se nos pide que expliquemos el significado de la expresión en palabras. La expresión interior en la composición es$s(3)$. Dado que la entrada a la$s$ función es tiempo, el 3 representa 3 minutos, y$s(3)$ es el número de abdominales que se pueden hacer en 3 minutos. Tomando esta salida y utilizarla como entrada a la$c(s)$ función nos dará las calorías que se pueden quemar por el número de abdominales que se pueden hacer en 3 minutos.

Composición de Funciones mediante Tablas y Gráficas

Al trabajar con funciones dadas como tablas y gráficas, podemos buscar valores para las funciones usando una tabla o gráfica proporcionada. Comenzamos la evaluación a partir de la entrada proporcionada, y primero evaluamos la función interna. Entonces podemos usar la salida de la función inside como la entrada a la función externa. Para recordar esto, siempre trabaja de adentro hacia afuera.

Ejemplo$\PageIndex{2}$

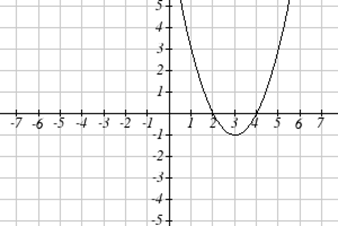
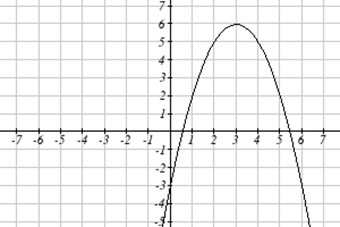
Usando las gráficas a continuación, evalúe$f(g(1))$.

$g(x)$

$f(x)$

Solución

Para evaluar$f(g(1))$, nuevamente comenzamos con la evaluación interna. Evaluamos$g(1)$ usando la gráfica de la$g(x)$ función, encontrando la entrada de 1 en el eje horizontal y encontrando el valor de salida de la gráfica en esa entrada. Aquí,$g(1)=3$. Usando este valor como entrada a la$f$ función,$f(g(1))=f(3)$. Luego podemos evaluar esto mirando a la gráfica de la$f(x)$ función, encontrando la entrada de 3 en el eje horizontal y leyendo el valor de salida de la gráfica en esta entrada. Aquí,$f(3)=6$, entonces$f(g(1))=6$.

Composiciones usando Fórmulas

Al evaluar una composición de funciones donde ya sea hemos creado o se nos han dado fórmulas, el concepto de trabajar de adentro hacia afuera sigue siendo el mismo. Primero evaluamos la función inside usando el valor de entrada proporcionado, luego usamos la salida resultante como la entrada a la función externa.

Ejemplo$\PageIndex{3}$

Dado$f(t)=t^2-t$ y$h(x)=3x+2$, evaluar$f(h(1))$.

Solución

Dado que la evaluación interna es$h(1)$ comenzamos evaluando la$h(x)$ función en 1:

$$h(1)=3(1)+2=5\nonumber$$

Luego$f(h(1))=f(5)$, así evaluamos la$f(t)$ función a una entrada de 5:

$$f(h(1))=f(5)=5^2-5=20\nonumber$$

No estamos limitados, sin embargo, a usar un valor numérico como entrada a la función. Podemos poner cualquier cosa en la función: un valor, una variable diferente, o incluso una expresión algebraica, siempre que usemos la expresión de entrada en todas partes donde veamos la variable de entrada.

Ejemplo$\PageIndex{4}$

Dejar$f(x)=x^2$ y$g(x)=\dfrac{1}{x}-2x$. Encontrar$f(g(x))$ y$g(f(x))$.

Solución

Para encontrar$f(g(x))$, comenzamos evaluando el interior, escribiendo la fórmula para$g(x)$:

$$g(x)=\dfrac{1}{x}-2x\nonumber$$

Luego usamos la expresión$\left(\dfrac{1}{x}-2x\right)$ como entrada para la función$f$:

$$f(g(x))=f\left(\dfrac{1}{x}-2x\right)\nonumber$$

Luego evaluamos la función$f(x)$ usando la fórmula para$g(x)$ como entrada. Desde$f(x)=x^2$ entonces

$$f\left(\dfrac{1}{x}-2x\right)=\left(\dfrac{1}{x}-2x\right)^2\nonumber$$

Esto nos da la fórmula para la composición:

$$f(g(x))=\left(\dfrac{1}{x}-2x\right)^2\nonumber$$

De igual manera$g(f(x))$, para encontrar, evaluamos el interior, escribiendo la fórmula para$f(x)$:$g(f(x))=g(x^2)$.

Ahora evaluamos la función$g(x)$ usando$x^2$ como entrada:

$$g(f(x))=\dfrac{1}{x^2}-2x^2\nonumber$$

Ejemplo$\PageIndex{5}$

Un administrador municipal determina que los ingresos fiscales,$R$, en millones de dólares recaudados a una población de$p$ mil personas, viene dado por la fórmula$R(p)=0.03p+\sqrt{p}$, y que se prevé que la población de la ciudad, en miles, siga la fórmula$p(t)=60+2t+0.3t^2$, donde$t$ se mide en años después de 2010. Encuentre una fórmula para los ingresos fiscales en función del año.

Solución

Como queremos que los ingresos fiscales sean una función del año, queremos que el año sea nuestro insumo inicial, y que los ingresos sean nuestro producto final. Para encontrar ingresos, primero tendremos que predecir la población de la ciudad, y luego usar ese resultado como insumo para la función fiscal. Entonces necesitamos encontrar$R(p(t)).$ Evaluando esto,

$$\begin{align*} R(p(t)) & = R(60+2t+0.3t^2)\\ & = 0.03(60+2t+0.3t^2)+\sqrt{60+2t+0.3t^2} \end{align*}\nonumber$$

Esta composición nos da una fórmula única que puede ser utilizada para predecir los ingresos fiscales durante un año determinado, sin necesidad de encontrar el valor de la población intermediaria.

Por ejemplo, para predecir los ingresos fiscales en 2017, cuando$t = 7$ (porque$t$ se mide en años posteriores a 2010),

$$\begin{align*} R(p(7)) & = 0.03\left(60+2(7)+0.3\left(7^2\right)\right)+\sqrt{60+2(7)+0.3\left(7^2\right)}\\ \approx & 12.079\text{ million dollars} \end{align*}\nonumber$$

Más adelante en este curso, será deseable descomponer una función —escribirla como una composición de dos funciones más simples.

Ejemplo$\PageIndex{6}$

Escribir$f(x)=3+\sqrt{5-x^2}$ como la composición de dos funciones.

Solución

Estamos buscando dos funciones,$g$ y$h$, entonces$f(x)=g(h(x))$. Para ello, buscamos una función dentro de una función en la fórmula para$f(x)$. Como una posibilidad, podríamos notar que$5-x^2$ es el interior de la raíz cuadrada. Entonces podríamos descomponer la función como:

$$h(x)=5-x^2, \quad g(x)=3+\sqrt{x}\nonumber$$

Podemos verificar nuestra respuesta recomponiendo las funciones:

$$g(h(x))=g(5-x^2)=3+\sqrt{5-x^2}\nonumber$$

Tenga en cuenta que esta no es la única solución al problema. Otra descomposición no trivial sería

$$h(x)=x^2, \quad g(x)=3+\sqrt{5-x}.\nonumber$$

Transformaciones de funciones

Las transformaciones nos permiten construir nuevas ecuaciones a partir de nuestras funciones básicas del kit de herramientas. Las transformaciones más básicas son desplazar la gráfica vertical u horizontalmente.

Desplazamiento vertical

Dada una función$f(x)$, si definimos una nueva función$g(x)$ como$g(x)=f(x)+k$, donde$k$ es una constante, entonces$g(x)$ es un desplazamiento vertical de la función$f(x)$, donde todos los valores de salida se han incrementado en$k$.

Si$k$ es positivo, entonces la gráfica se desplazará hacia arriba. Si$k$ es negativo, entonces la gráfica se desplazará hacia abajo.

Desplazamiento Horizontal

Dada una función$f(x)$, si definimos una nueva función$g(x)$ como$g(x)=f(x+k)$, donde$k$ es una constante, entonces$g(x)$ es un desplazamiento horizontal de la función$f(x)$, donde todos los valores de salida se han incrementado en$k$.

Si$k$ es positivo, entonces la gráfica se desplazará a la izquierda. Si$k$ es negativo, entonces la gráfica se desplazará a la derecha.

Ejemplo$\PageIndex{7}$

Dado$f(x)=|x|$, esbozar una gráfica de$h(x)=f(x+1)-3=|x+1|-3$.

Solución

La función$f$ es nuestra función de valor absoluto de kit de herramientas. Sabemos que esta gráfica tiene forma de V, con el punto en el origen. La gráfica de se$h$ ha transformado$f$ de dos maneras:$f(x+1)$ es un cambio en el interior de la función, dando un desplazamiento horizontal a la izquierda por 1, luego la resta por 3 in$f(x+1)-3$ es un cambio al exterior de la función, dando un desplazamiento vertical hacia abajo por 3. Transformar la gráfica da:

Ejemplo$\PageIndex{8}$

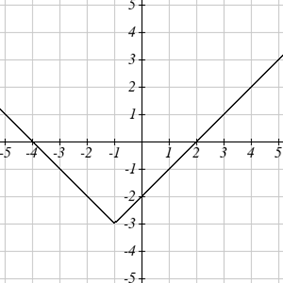
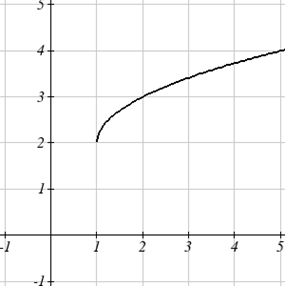
Escribe una fórmula para la gráfica mostrada, una transformación de la función de raíz cuadrada del kit de herramientas.

Solución

La gráfica de la función del kit de herramientas comienza en el origen, por lo que esta gráfica se ha desplazado 1 a la derecha, y hacia arriba 2. En notación de funciones, podríamos escribir eso como$h(x)=f(x-1)+2$. Usando la fórmula para la función de raíz cuadrada podemos escribir$h(x)=\sqrt{x-1}+2$.

Tenga en cuenta que esta transformación ha cambiado el dominio y el rango de la función. Esta nueva gráfica tiene dominio$[1,\infty)$ y rango$[2,\infty)$.

Otra transformación que se puede aplicar a una función es una reflexión sobre el eje horizontal o vertical.

Reflexiones

Dada una función$f(x)$, si definimos una nueva función$g(x)$ como$-f(x)$, entonces$g(x)$ es una reflexión vertical de la función$f(x)$, a veces llamada reflexión sobre el eje x

Si definimos una nueva función$g(x)$ como$f(-x)$, entonces$g(x)$ es una reflexión horizontal de la función$f(x)$, a veces llamada reflexión sobre el$y$ eje -eje.

Ejemplo$\PageIndex{9}$

Un modelo común para el aprendizaje tiene una ecuación similar a$k(t)=-2^t+1$, donde$k$ está el porcentaje de dominio que se puede lograr después de las sesiones de$t$ práctica. Esta es una transformación de la función aquí$f(t)=2^t$ mostrada. Esbozar una gráfica de$k(t)$.

$f(t)=2^t$

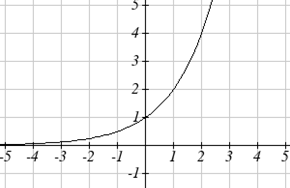
Solución

Esta ecuación combina tres transformaciones en una sola ecuación.

Una reflexión horizontal:	$f(-t)=2^{-t}$	combinado con
una reflexión vertical:	$-f(-t)=-2^{-t}$	combinado con
un desplazamiento vertical hacia arriba 1:	$-f(-t)+1=-2^{-t}+1$.

Podemos esbozar una gráfica aplicando estas transformaciones una a la vez a la función original:

La gráfica original

Reflejado horizontalmente

Luego se refleja verticalmente

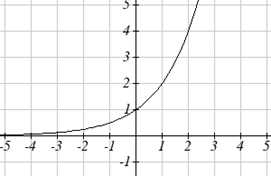
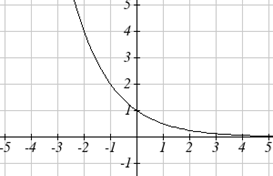
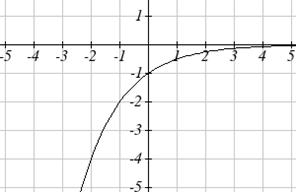
Luego, después de subir 1, obtenemos la gráfica final:

$$k(t)=-f(-t)+1=-2^{-t}+1\nonumber$$

Gráfica final

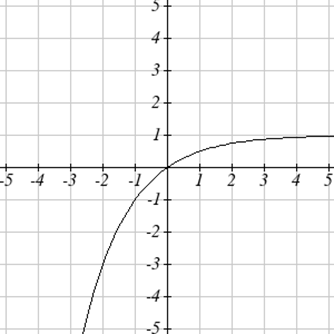
Nota: Como modelo de aprendizaje, esta función estaría limitada a un dominio de$t\geq 0$, con rango correspondiente$[0,1)$.

Con los turnos, vimos el efecto de sumar o restar a las entradas o salidas de una función. Ahora exploramos los efectos de multiplicar las salidas.

Estiramiento/Compresión Vertical

Dada una función$f(x)$, si definimos una nueva función$g(x)$ como$g(x)=k\cdot f(x)$, donde$k$ es una constante, entonces$g(x)$ es un estiramiento vertical o compresión de la función$f(x)$.

• Si$k \gt 1$, entonces la gráfica se estirará
• Si$0\lt k \lt 1$, entonces la gráfica se comprimirá
• Si$k \lt 0$, entonces habrá combinación de un estiramiento vertical o compresión con una reflexión vertical

Ejemplo$\PageIndex{10}$

La gráfica a continuación es una transformación de la función del kit de herramientas$f(x)=x^3$. Relacionar esta nueva función$g(x)$ con$f(x)$, luego encontrar una fórmula para$g(x)$.

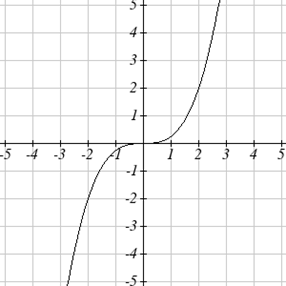
Solución

Al tratar de determinar un estiramiento o desplazamiento vertical, es útil buscar un punto en la gráfica que sea relativamente claro. En esta gráfica, aparece que$g(2)=2$. Con la función cúbica básica en la misma entrada,$f(2)=2^3=8$. En base a eso, parece que las salidas de$g$ son$\frac{1}{4}$ las salidas de la función$f$, ya que$g(2)=\frac{1}{4}f(x)$. De esto podemos concluir con bastante seguridad que

$$g(x)=\frac{1}{4}f(x).\nonumber$$

Podemos escribir una fórmula para$g$ usando la definición de la función$f$:

$$g(x)=\frac{1}{4}f(x)=\frac{1}{4}x^3.\nonumber$$

Combinando Transformaciones

Al combinar transformaciones verticales, es muy importante considerar el orden de las transformaciones. Por ejemplo, el desplazamiento vertical en 3 y luego el estiramiento vertical en 2 no crea la misma gráfica que el estiramiento vertical por 2 y luego el desplazamiento vertical en 3. El orden sigue muy bien del orden de operaciones.

Combinando transformaciones verticales

Al combinar transformaciones verticales escritas en la forma$a\cdot f(x)+k$, primero estira verticalmente por$a$, luego desplazarlo verticalmente por$k$.

Ejemplo$\PageIndex{11}$

Escribe una ecuación para la gráfica transformada de la función cuadrática mostrada.

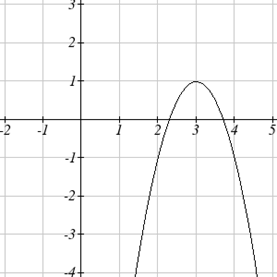
Solución

Dado que esta es una función cuadrática, primero considere cómo se ve la función básica del kit de herramientas cuadráticas y cómo ha cambiado esto. Observando la gráfica, notamos varias transformaciones: La función del kit de herramientas original se ha volteado sobre el$x$ eje, se ha producido algún tipo de estiramiento o compresión, y podemos ver un desplazamiento hacia la derecha 3 unidades y un cambio hacia arriba 1 unidad. En total hay cuatro operaciones:

1. Reflexión vertical, requiriendo un signo negativo fuera de la función.
2. Estiramiento Vertical
3. Desplazamiento Horizontal Derecha 3 unidades, lo que nos indica poner x-3 en el interior de la función.
4. Vertical Shift up 1 unidad, diciéndonos que agreguemos 1 en el exterior de la función.

Por observación, la función básica del kit de herramientas tiene un vértice en (0, 0) y puntos simétricos en (1, 1) y (-1, 1). Estos puntos son 1 unidad hacia arriba y 1 unidad por encima del vértice. Los nuevos puntos en la gráfica transformada están a 1 unidad horizontalmente pero a 2 unidades verticalmente. Se han estirado verticalmente por 2.

No todo el mundo puede ver esto simplemente mirando la gráfica. Si puedes, genial, pero si no podemos resolverlo. Primero, escribiremos la ecuación para esta gráfica, con un estiramiento vertical desconocido:

$f(x)=x^2$	La función original
$-f(x)=-x^2$	Reflejado verticalmente
$-a\cdot f(x)=-a x^2$	Estirados verticalmente
$-a\cdot f(x-3)=-a(x-3)^2$	Desplazado derecho 3
$-a\cdot f(x-3)+1=-a(x-3)^2+1$	Desplazado hacia arriba 1

Ahora sabemos que nuestra gráfica va a tener una ecuación de la forma$g(x)=-a(x-3)^2+1$. Para encontrar el estiramiento vertical, podemos identificar cualquier punto de la gráfica (que no sea el punto más alto), como el punto (2, -1), que nos dice$g(2)=-1$. Usando nuestra fórmula general, y sustituyendo 2 por$x$, y -1 por$g(x)$.

Esto nos dice que para producir la gráfica necesitamos un estiramiento vertical por dos.

Así, la función que produce esta gráfica es

$$g(x)=-2(x-3)^2+1.\nonumber$$

Ejemplo$\PageIndex{12}$

¿En qué intervalo (s)$g(x)=\dfrac{-2}{(x-1)^2}+3$ aumenta y disminuye la función?

Solución

Se trata de una transformación de la función recíproca al cuadrado del conjunto de herramientas,$f(x)=\dfrac{1}{x^2}$

$-2f(x)=\dfrac{-2}{x^2}$	Un volteo vertical y estiramiento vertical por 2
$-2f(x-1)=\dfrac{-2}{(x-1)^2}$	Un desplazamiento a la derecha por 1
$-2f(x-1)+3=\dfrac{-2}{(x-1)^2}+3$	Un cambio hacia arriba por 3

La función básica recíproca al cuadrado está aumentando$(-\infty,0)$ y disminuyendo en$(0,\infty)$. Debido al giro vertical, la$g(x)$ función estará disminuyendo a la izquierda y aumentando a la derecha. El desplazamiento horizontal a la derecha en 1 también desplazará estos intervalos a la derecha. A partir de esto, podemos determinar que$g(x)$ va a aumentar$(1,\infty)$ y disminuir en$(-\infty,1)$. También podríamos graficar la transformación para ayudarnos a determinar estos intervalos.

Gráfica de la función transformada.