1.E: Revisión (Ejercicios)
- Page ID
- 110561
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)1.1 Ejercicios
La cantidad de basura,\(G\), producida por una ciudad con población\(p\) viene dada por\(G = f(p)\). \(G\)se mide en toneladas por semana, y\(p\) se mide en miles de personas.
- El poblado de Tola tiene una población de 40,000 y produce 13 toneladas de basura cada semana. Exprese esta información en términos de la función\(f\).
- Explique el significado de la declaración\(f(5) = 2\).
El número de yardas cúbicas de tierra\(D\),, necesario para cubrir un jardín con área pies\(a\) cuadrados viene dado por\(D = g(a)\).
- Un jardín con área 5000\(ft^2\) requiere 50 yardas cúbicas de tierra. Exprese esta información en términos de la función\(g\).
- Explique el significado de la declaración\(g(100) = 1\).
Seleccione todas las siguientes gráficas que representen\(y\) como una función de\(x\).
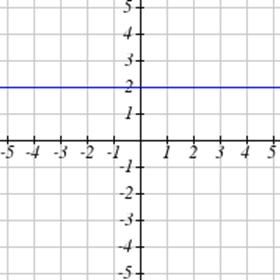
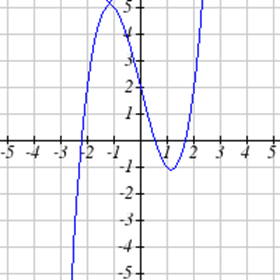
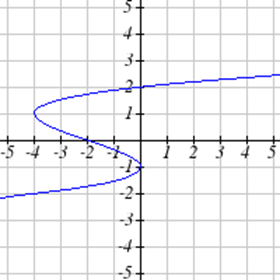
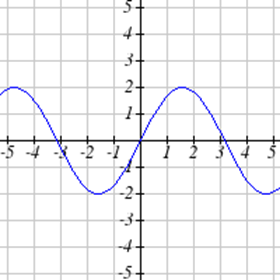
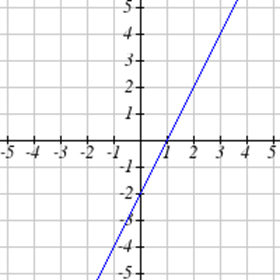
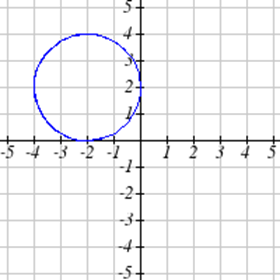
Seleccione todas las siguientes gráficas que representen\(y\) como una función de\(x\).
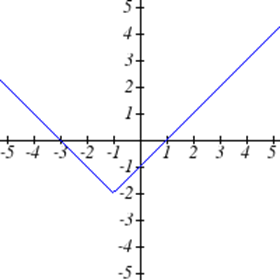
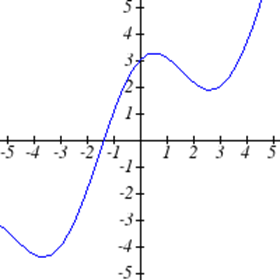
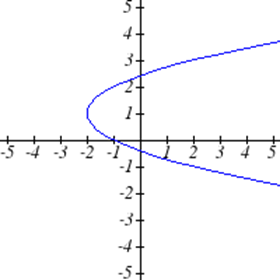
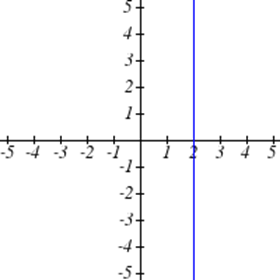
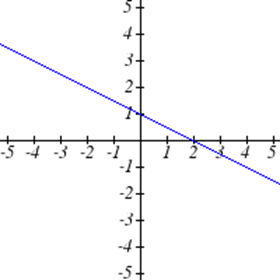
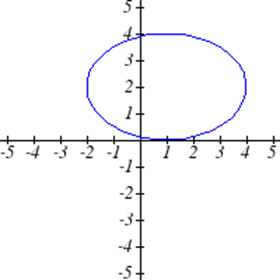
Seleccione todas las tablas siguientes que representan\(y\) como una función de\(x\).
a.
|
x |
5 |
10 |
15 |
|
y |
3 |
8 |
14 |
b.
|
x |
5 |
10 |
15 |
|
y |
3 |
8 |
8 |
c.
|
x |
5 |
10 |
10 |
|
y |
3 |
8 |
14 |
Seleccione todas las tablas siguientes que representan\(y\) como una función de\(x\).
a.
|
x |
2 |
6 |
13 |
|
y |
3 |
10 |
10 |
b.
|
x |
2 |
6 |
6 |
|
y |
3 |
10 |
14 |
c.
|
x |
2 |
6 |
13 |
|
y |
3 |
10 |
14 |
Dada la función\(g(x)\) graficada aquí,
- Evaluar\(g(2)\)
- Resolver\(g(x) = 2\)
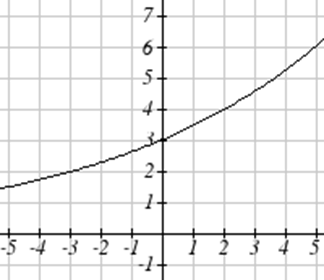
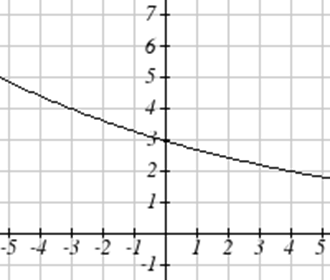
Dada la función\(f(x)\) graficada aquí.
- Evaluar\(f(4)\)
- Resolver\(f(x) = 4\)
Sobre la base del cuadro que figura a continuación,
- Evaluar\(f(3)\)
- Resolver\(f(x) = 1\)
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
74 |
28 |
1 |
53 |
56 |
3 |
36 |
45 |
14 |
47 |
Sobre la base del cuadro que figura a continuación,
- Evaluar\(f(8)\)
- Resolver\(f(x) = 7\)
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
\(f(x)\) |
62 |
8 |
7 |
38 |
86 |
73 |
70 |
39 |
75 |
34 |
Para cada una de las siguientes funciones, evaluar:\(f(-2)\),\(f(-1)\),\(f(0)\),\(f(1)\), y\(f(2)\)
| 11. \(f(x) = 4-2x\) | 12. \(f(x) = 8 - 3x\) |
| 13. \(f(x) = 8x^2 - 7x + 3\) | 14. \(f(x) = 6x^2 -7x+4\) |
| 15. \(f(x) = 3 + \sqrt{x+3}\) | 16. \(f(x) = 4 - \sqrt[3]{x-2}\) |
| 17. \(f(x) = \frac{x-3}{x+1}\) | 18. \(f(x) = \frac{x-2}{x+2}\) |
Let\(f(t) = 3t+5\)
- Evaluar\(f(0)\)
- Resolver\(f(t) = 0\)
Let\(g(p) = 6 - 2p\)
- Evaluar\(g(0)\)
- Resolver\(g(p) = 0\)
Usando la gráfica mostrada,
- Evaluar\(f(c)\)
- Resolver\(f(x) = p\)
- ¿Cuáles son las coordenadas de los puntos\(L\) y\(K\)?
Coincide cada gráfica con su ecuación.
| a.\(y=x\) | b.\(y = x^3\) | \(y = \sqrt[3]{x}\) | d.\(y = \frac{1}{x}\) |
| e.\(y = x^2\) | f.\(y = \sqrt{x}\) | g.\(y = |x|\) | h.\(y = \frac{1}{x^2}\) |
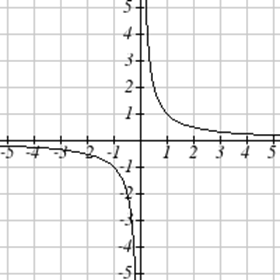
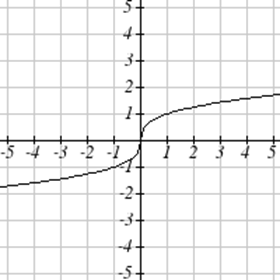
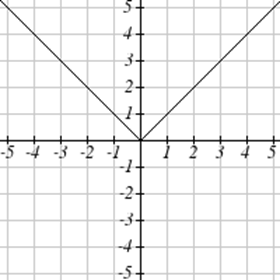
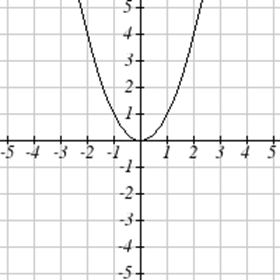
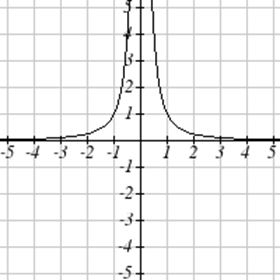
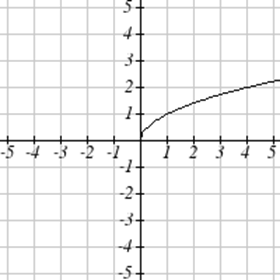
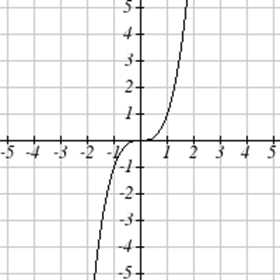
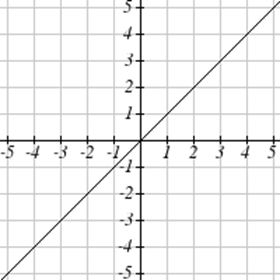
Para Ejercicios\(\PageIndex{23}-\PageIndex{24}\), escriba el dominio y el rango de cada gráfica como una desigualdad.
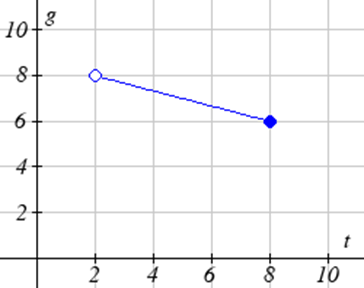
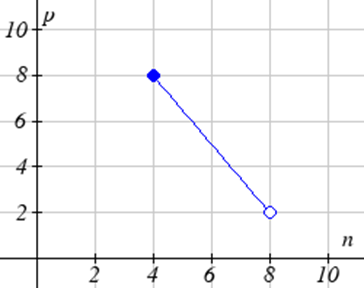
Encuentra el dominio de cada función.
| 25. \(f(x) = 3\sqrt{x-2}\) | 26. \(f(x) = 5\sqrt{x+3}\) |
| 27. \(f(x) = \frac{9}{x-6}\) | 28. \(f(x) = \frac{6}{x-8}\) |
| 29. \(f(x) = \frac{3x+1}{4x+2}\) | 30. \(f(x) = \frac{5x+3}{4x-1}\) |
1.2 Ejercicios
| 1. \(f(x) = 4x+8, g(x) = 7-x^2\) | 2. \(f(x) = 5x+7, g(x) = 4-2x^2\) |
| 3. \(f(x) = \sqrt{x+4}, g(x) = 12-x^3\) | 4. \(f(x) = \frac{1}{x+2}, g(x) = 4x+3\) |
|
x |
\(f(x)\) |
\(g(x)\) |
|
0 |
7 |
9 |
|
1 |
6 |
5 |
|
2 |
5 |
6 |
|
3 |
8 |
2 |
|
4 |
4 |
1 |
|
5 |
0 |
8 |
|
6 |
2 |
7 |
|
7 |
1 |
3 |
|
8 |
9 |
4 |
|
9 |
3 |
0 |
Utilice la tabla de valores para evaluar cada expresión.
| 5. \(f(g(8))\) |
| 6. \(f(g(5))\) |
| 7. \(g(f(5))\) |
| 8. \(g(f(3))\) |
| 9. \(f(f(4))\) |
| 10. \(f(f(1))\) |
| 11. \(g(g(2))\) |
| 12. \(g(g(6))\) |
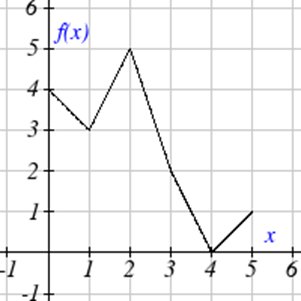
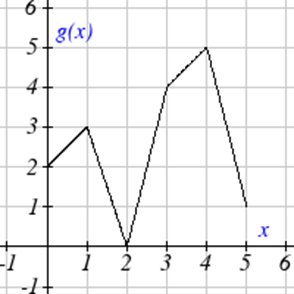
Utilice las gráficas para evaluar las expresiones que aparecen a continuación.
| 13. \(f(g(3))\) |
| 14. \(f(g(1))\) |
| 15. \(g(f(1))\) |
| 16. \(g(f(0))\) |
| 17. \(f(f(5))\) |
| 18. \(f(f(4))\) |
| 19. \(g(g(2))\) |
| 20. \(g(g(0))\) |
Para cada par de funciones, buscar\(f(g(x))\) y\(g(f(x))\). Simplifica tus respuestas.
| 21. \(f(x) = \frac{1}{x-6}, g(x) = \frac{7}{x}+6\) | 22. \(f(x) = \frac{1}{x-4}, g(x) = \frac{2}{x} + 4\) |
| 23. \(f(x) = x^2+1, g(x) = \sqrt{x+2}\) | 24. \(f(x) = \sqrt{x} + 2, g(x) = x^2 + 3\) |
| 25. \(f(x) = |x|, g(x) = 5x+1\) | 26. \(f(x) = \sqrt[3]{x}, g(x) = \frac{x+1}{x^3}\) |
Si\(f(x) = x^4+6\),\(g(x) = x - 6\), y\(h(x) = \sqrt{x}\), encontrar\(f(g(h(x)))\)
Si\(f(x) = x^2+1\),\(g(x) = \frac{1}{x}\), y\(h(x) = x+3\), encontrar\(f(g(h(x)))\)
La función\(D(p)\) da el número de artículos que se exigirán cuando el precio sea\(p\). El costo de producción,\(C(x)\) es el costo de producir\(x\) artículos. Para determinar el costo de producción cuando el precio es de $6, usted haría cuál de las siguientes acciones:
- Evaluar\(D(C(6))\)
- Resolver\(C(D(6))\)
- Evaluar\(D(C(x)) = 6\)
- Resolver\(C(D(p)) = 6\)
La función\(A(d)\) da el nivel de dolor en una escala de 0-10 experimentado por un paciente con\(d\) miligramos de un medicamento para la reducción del dolor en su sistema. Los miligramos de fármaco en el sistema del paciente después de\(t\) minutos son modelados por\(m(t)\). Para determinar cuándo el paciente estará en un nivel de dolor de 4, se necesitaría:
- Evaluar\(A(m(4))\)
- Resolver\(m(A(4))\)
- Evaluar\(A(m(t)) = 4\)
- Resolver\(m(A(d)) = 4\)
Buscar funciones\(f(x)\) y\(g(x)\) así la función dada se puede expresar como\(h(x) = f(g(x))\).
| 31. \(h(x) = (x+2)^2\) | 32. \(h(x) = (x-5)^3\) |
| 33. \(h(x) = \frac{3}{x-5}\) | 34. \(h(x) = \frac{4}{(x+2)^2}\) |
| 35. \(h(x) = 3+\sqrt{x-2}\) | 36. \(h(x) = 4+\sqrt[3]{x}\) |
Esboce un gráfico de cada función como una transformación de una función de kit de herramientas.
| 37. \(f(t) = (t+1)^2 - 3\) | 38. \(h(x) = |x-1|+4\) |
| 39. \(k(x) =(x-2)^3 -1\) | 40. \(m(t) = 3+\sqrt{t+2}\) |
| 41. \(f(x) = 4(x+1)^2 - 5\) | 42. \(g(x) = 5(x+3)^2 - 2\) |
| 43. \(h(x) = -2|x-4|+3\) | 44. \(k(x) = -3\sqrt{x} - 1\) |
Escribe una ecuación para cada función graficada a continuación.
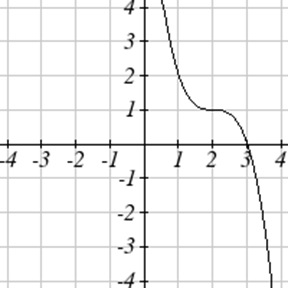
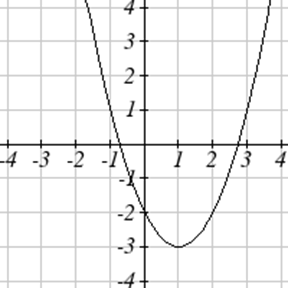
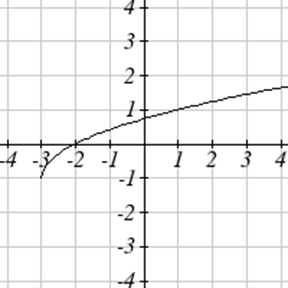
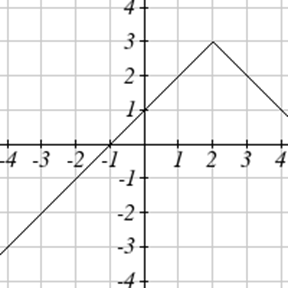
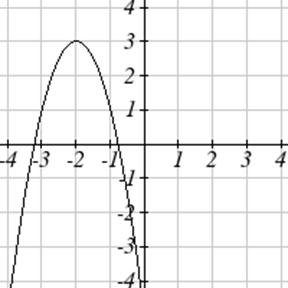
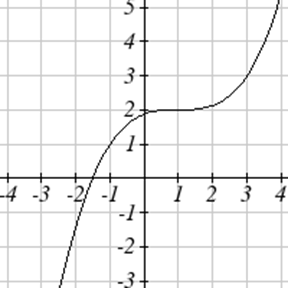
Para cada función graficada, estime los intervalos en los que la función está aumentando y disminuyendo.
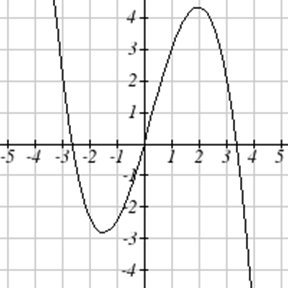
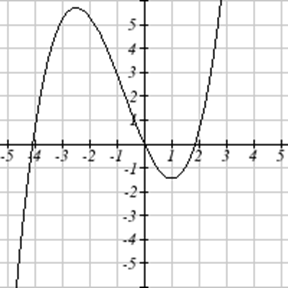 52.
52.1.3 Ejercicios
La población de un pueblo ha ido creciendo linealmente. En 2003, la población era de 45 mil, y la población ha ido creciendo en 1700 personas cada año. Escribir una ecuación,\(P(t)\), para la población\(t\) años posteriores a 2003.
La población de un pueblo ha ido creciendo linealmente. En 2005, la población era de 69 mil, y la población ha ido creciendo en 2500 personas cada año. Escribir una ecuación,\(P(t)\), para la población\(t\) años posteriores a 2005.
Timmy va a la feria con $40. Cada viaje cuesta $2. ¿Cuánto dinero le quedará después de montar\(n\) en bicicleta?
Al mediodía, una barista se da cuenta de que tiene 20 dólares en su jarra de propinas. Si gana un promedio de $0.50 por cada cliente, ¿cuánto tendrá en su bote de propinas si atiende a\(n\) más clientes durante su turno?
Una compañía telefónica cobra por el servicio de acuerdo a la fórmula:\(C(n) = 24+0.1n\), dónde\(n\) está el número de minutos platicado, y\(C(n)\) es el cargo mensual, en dólares.
Encuentra e interpreta la tasa de cambio y el valor inicial.
Una compañía telefónica cobra por el servicio de acuerdo a la fórmula:\(C(n) = 26+0.04n\), dónde\(n\) está el número de minutos platicado, y\(C(n)\) es el cargo mensual, en dólares.
Encuentra e interpreta la tasa de cambio y el valor inicial.
Dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones, si es posible.
| 7. \(f(-5) = -4\), y\(f(5)=2\) | 8. \(f(-1)=4\), y\(f(5)=1\) |
| 9. Pasa a través de (2,4) y (4,10) | 10. Pasa a través de (1, 5) y (4, 11) |
| 11. Pasa a través de (-1,4) y (5, 2) | 12. Pasa a través de (-2, 8) y (4, 6) |
| 13. \(x\)interceptar en (-2, 0) e\(y\) interceptar en (0, -3) | 14. \(x\)interceptar en (-5, 0) e\(y\) interceptar en (0, 4) |
Encuentra una ecuación para la función graficada.
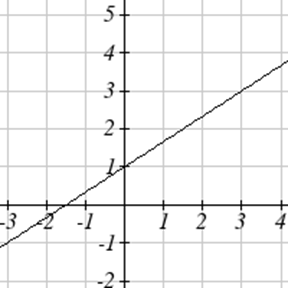
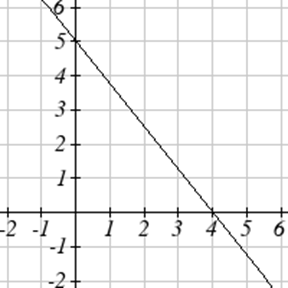
Un negocio de ropa encuentra que existe una relación lineal entre el número de camisas\(n\),, puede vender y el precio\(p\),, puede cobrar por camisa. En particular, los datos históricos muestran que se pueden vender 1000 playeras a un precio de 30 dólares, mientras que 3000 camisas se pueden vender a un precio de 22 dólares. Encuentra una ecuación lineal en la forma\(p=mn+b\) que dé el precio\(p\) que pueden cobrar por las\(n\) camisas.
Un agricultor encuentra que existe una relación lineal entre el número de tallos de frijol\(n\),, ella planta y el rendimiento,\(y\), cada planta produce. Cuando planta 30 tallos, cada planta produce 30 oz de frijoles. Cuando planta 34 tallos, cada planta produce 28 oz de frijoles. Encuentra una relación lineal en la forma\(y=mn+b\) que da el rendimiento cuando se plantan\(n\) tallos.
Coincide cada ecuación lineal con su gráfica
| 19. \(f(x) = -x-1\) |
| 20. \(f(x) = -2x-1\) |
| 21. \(f(x) = -\frac{1}{2}x-1\) |
| 22. \(f(x) = 2\) |
| 23. \(f(x) = 2+x\) |
| 24. \(f(x) = 3x+2\) |
Esbozar la gráfica de cada ecuación
| 25. \(f(x) = -2x-1\) | 26. \(g(x) = -3x+2\) |
| 27. \(h(x)=\frac{1}{3}x+2\) | 28. \(k(x) = \frac{2}{3}x-3\) |
Encuentra el punto en el que la línea\(f(x) = -2x-1\) se cruza con la línea\(g(x)=-x\)
Encuentra el punto en el que la línea\(f(x)=2x+5\) se cruza con la línea\(g(x)=-3x-5\)
Una empresa de alquiler de autos ofrece dos planes para rentar un auto.
Plan A: 30 dólares por día y 18 centavos por milla
Plan B: 50 dólares por día con kilometraje ilimitado gratuito
¿Cuántas millas necesitarías conducir para el plan B para ahorrarte dinero?
Una compañía de telefonía celular ofrece dos opciones de datos para sus teléfonos prepagos
Pago por uso: $0.002 por Kilobyte (KB) usado
Paquete de Datos: $5 por 5 Megabytes (5120 Kilobytes) + $0.002 por KB adicional
Suponiendo que usará menos de 5 Megabytes, ¿bajo qué circunstancias el paquete de datos le ahorrará dinero?
La Reserva Federal de Helio tenía alrededor de 16 mil millones de pies cúbicos de helio en 2010, y se está agotando en alrededor de 2.1 mil millones de pies cúbicos cada año.
- Dar una ecuación lineal para el resto de las reservas federales de helio\(R\), en términos de\(t\), el número de años desde 2010.
- En 2015, ¿cuáles serán las reservas de helio?
- Si la tasa de agotamiento no cambia, ¿cuándo se agotará la Reserva Federal de Helio?
Supongamos que las actuales reservas mundiales de petróleo son de 1820 mil millones de barriles. Si, en promedio, las reservas totales están disminuyendo en 25 mil millones de barriles de petróleo cada año:
- Dar una ecuación lineal para las reservas de petróleo restantes,\(R\), en términos de\(t\), el número de años transcurridos desde ahora.
- Dentro de siete años, ¿cuáles serán las reservas petroleras?
- Si no cambia la tasa de agotamiento, ¿cuándo se agotarán las reservas mundiales de petróleo?
1.4 Ejercicios
Simplificar cada expresión
| 1. \(x^3x^5\) | 2. \(x^4x^2\) |
| 3. \(\left(x^3\right)^4\) | 4. \(\left(x^7\right)^2\) |
| 5. \(\left(2x^2\right)^3x^4\) | 6. \(\left(5x^4\right)^2x^5\) |
| 7. \(\frac{\left(3x^2\right)^2}{6x^3}\) | 8. \(\frac{5x\left(4x\right)^2}{2x^2}\) |
Simplifique y reescriba sin exponentes negativos
| 9. \(4x^{-3}\) | 10. \(2x^{-5}\) |
| 11. \(x^{-4}x^2\) | 12. \(x^{-2}x\) |
| 13. \(\frac{5x^{-3}}{2x^{-6}}\) | 14. \(\frac{2x^{-4}}{6x^{-2}}\) |
Reescribir usando exponentes negativos o fraccionarios
| 15. \(\frac{4}{x^{-5}}\) | 16. \(\frac{4}{x^{-3}}\) |
| 17. \(3\sqrt{x}\) | 18. \(\sqrt[4]{x}\) |
| 19. \(\frac{4}{\sqrt[3]{x}}\) | 20. \(\frac{1}{5\sqrt{x}}\) |
Reescribir como radical
| 21. \(4x^{-\frac{1}{2}}\) | 22. \(5x^{-\frac{1}{3}}\) |
| 23. \(2x^{\frac{1}{3}}\) | 24. \(5x^{\frac{3}{2}}\) |
1.5 Ejercicios
Escribe una ecuación para la función cuadrática graficada.
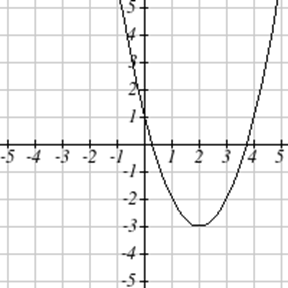
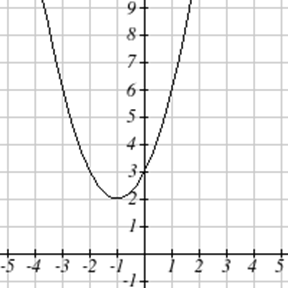
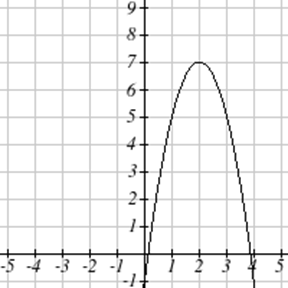
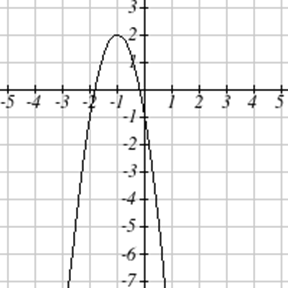
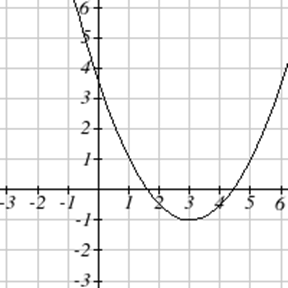
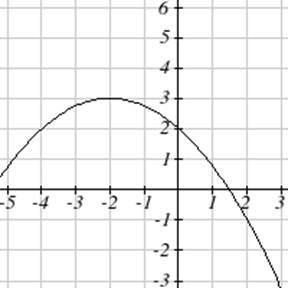
| 7. \(y(x) = 2x^2+10x+12\) | 8. \(z(p)=3x^2+6x-9\) |
| 9. \(f(x)=2x^2-10x+4\) | 10. \(g(x) = -2x^2-14x+12\) |
| 11. \(h(t)=-4t^2+6t-1\) | 12. \(k(t) = 2x^2+4x-15\) |
La altura de una pelota lanzada al aire viene dada por\(h(x) = -\frac{1}{12}x^2+6x+3\), donde\(x\) está la distancia horizontal en pies desde el punto en el que se lanza la pelota.
- ¿Qué tan alto es el balón cuando fue arrojado?
- ¿Cuál es la altura máxima de la pelota?
- ¿A qué distancia del lanzador golpea el balón al suelo?
Se lanza una jabalina al aire. Su altura viene dada por\(h(x)=-\frac{1}{20}x^2+8x+6\), donde\(x\) está la distancia horizontal en pies desde el punto en el que se lanza la jabalina.
- ¿Qué tan alta es la jabalina cuando la tiraron?
- ¿Cuál es la altura máxima de la jabalina?
- ¿A qué distancia del lanzador golpea el suelo la jabalina?
1.6 Ejercicios
Encuentra el grado y coeficiente principal de cada polinomio
| 1. \(4x^7\) | 2. \(5x^6\) |
| 3. \(5-x^2\) | 4. \(6+3x-4x^3\) |
| 5. \(-2x^4-3x^2+x-1\) | 6. \(6x^5-2x^4+x^2+3\) |
Encuentra las intercepciones verticales y horizontales de cada función.
| 7. \(f(t) = 2(t-1)(t+2)(t-3)\) | 8. \(f(x)=3(x+1)(x-4)(x+5)\) |
| 9. \(g(n) = -2(3n-1)(2n+1)\) | 10. \(k(u)=-3(4-n)(4n+3)\) |
| 11. \(C(t) = 2t^4-8t^3+6t^2\) | 12. \(C(t)=4t^4+12t^3-40t^2\) |
Usa tu calculadora u otra tecnología gráfica para resolver gráficamente los ceros de la función.
| 13. \(f(x) = x^3 - 7x^2+4x+30\) | 14. \(g(x)=x^3-6x^2+x+28\) |
Resolver cada desigualdad.
| 15. \((x-3)(x-2)^2>0\) | 16. \((x-5)(x+1)^2>0\) |
| 17. \((x-1)(x+2)(x-3)<0\) | 18. \((x-4)(x+3)(x+6)<0\) |
Para cada función, encuentra las intercepciones horizontales, la intercepción vertical, las asíntotas verticales y la asíntota horizontal.
| 19. \(p(x) = \frac{2x-3}{x+4}\) | 20. \(q(x) = \frac{x-5}{3x-1}\) |
| 21. \(s(x) = \frac{4}{(x-2)^2}\) | 22. \(r(x) = \frac{5}{(x+1)^2}\) |
| 23. \(f(x) = \frac{3x^2-14x-5}{3x^2+8x-16}\) | 24. \(g(x) = \frac{2x^2+7x-15}{3x^2-14+15}\) |
| 25. \(h(x) = \frac{2x^2+x-1}{x-4}\) | 26. \(k(x) = \frac{2x^2-3x-20}{x-5}\) |
Un científico tiene un vaso de precipitados que contiene 20 mL de una solución que contiene 20% de ácido. Para diluir esto, agrega agua pura.
- Escribe una ecuación para la concentración en el vaso de precipitados después de agregar\(n\) mL de agua.
- Encuentra la concentración si se han agregado 10 mL de agua.
- ¿Cuántos mL de agua se deben agregar para obtener una solución al 4%?
- ¿Cuál es el comportamiento como\(n \to \infty\), y cuál es el significado físico de esto?
Un científico tiene un vaso de precipitados que contiene 30 mL de una solución que contiene 3 gramos de hidróxido de potasio. Para ello, mezcla una solución que contiene 8 miligramos por mL de hidróxido de potasio.
- Escribe una ecuación para la concentración en el tanque después de agregar\(n\) mL de la segunda solución.
- Encuentra la concentración si se han agregado 10 mL de la segunda solución.
- ¿Cuántos mL de agua se deben agregar para obtener una solución de 50 mg/mL?
- ¿Cuál es el comportamiento como\(n \to \infty\), y cuál es el significado físico de esto?
1.7 Ejercicios
Una población asciende inicialmente a 11 mil organismos y crece 8.5% cada año. Escribir un modelo exponencial para la población.
Actualmente una población es de 6 mil y ha ido aumentando 1.2% cada día. Escribir un modelo exponencial para la población.
Un vehículo adquirido por $32,500 se deprecia a una tasa constante de 5% cada año. Determinar el valor aproximado del vehículo 12 años después de la compra.
Una empresa compra $125,000 de muebles de oficina que se deprecian a una tasa constante de 12% cada año. Encuentra el valor residual de los muebles 6 años después de la compra.
Si se invierten $4,000 en una cuenta bancaria a una tasa de interés del 7 por ciento anual, encuentra el monto en el banco después de 9 años si los intereses se componen anual, trimestral, mensual y continuamente.
Si se invierten $6,000 en una cuenta bancaria a una tasa de interés del 9 por ciento anual, encuentra el monto en el banco después de 5 años si los intereses se componen anual, trimestral, mensual y continuamente.
Haga coincidir cada función con una de las gráficas a continuación.
| 7. \(f(x) = 2(0.69)^x\) |
| 8. \(f(x) = 2(1.28)^x\) |
| 9. \(f(x) = 2(0.81)^x\) |
| 10\(f(x) = 4(1.28)^x\) |
| 11. \(f(x) = 2(1.59)^x\) |
| 12. \(f(x) = 4(0.69)^x\) |
Si todas las gráficas de la derecha tienen ecuaciones con forma\(f(t) = ae^{kt}\),
|
13. ¿Para qué gráfica tiene el mayor valor\(k\)? |
|
14. ¿Para qué gráfica tiene el valor más pequeño\(k\)? |
|
15. ¿Para qué gráfica tiene el mayor valor\(a\)? |
|
16. ¿Para qué gráfica tiene el valor más pequeño\(a\)? |
1.8 Ejercicios
Reescribir cada ecuación en forma exponencial
| 1. \(\log (v) = t\) | 2. \(\log (r) = s\) | 3. \(\ln (w) = n\) | 4. \(\ln (x) = y\) |
Reescribe cada ecuación en forma logarítmica.
| 5. \(10^a = b\) | 6. \(10^p = v\) | 7. \(e^k = h\) | 8. \(e^y = x\) |
Resuelve cada ecuación para la variable.
| 9. \(5^{x} = 14\) | 10. \(3^x = 23\) | 11. \(7^x = \frac{1}{15}\) | 12. \(3^x = \frac{1}{4}\) |
| 13. \(e^{5x} = 17\) | 14. \(e^{3x} = 12\) | 15. \(3^{4x-5} = 38\) | 16. \(4^{2x-3} = 44\) |
| 17. \(1000(1.03)^t = 5000\) | 18. \(200(1.06)^t = 550\) |
| 19. \(3(1.04)^{3t} = 8\) | 20. \(2(1.08)^{4t} = 7\) |
| 21. \(50e^{-0.12t} = 10\) | 22. \(10e^{-0.03t} = 4\) |
| 23. \(10 - 8 \left(\frac{1}{2}\right)^x = 5\) | 24. \(100-100\left(\frac{1}{4}\right)^x = 70\) |
La población de Kenia era de 39.8 millones en 2009 y ha ido creciendo alrededor de 2.6% cada año. Si esta tendencia continúa, ¿cuándo superará la población los 45 millones?
La población de Argelia era de 34.9 millones en 2009 y ha ido creciendo alrededor de 1.5% cada año. Si esta tendencia continúa, ¿cuándo superará la población los 45 millones?
Si se invierte $1000 en una cuenta que gana 3% compuesto mensualmente, ¿cuánto tiempo tardará la cuenta en crecer en valor a 1500 dólares?
Si se invierten 1000 dólares en una cuenta que gana 2% compuesto trimestralmente, ¿cuánto tiempo tardará la cuenta en crecer en valor a 1300 dólares?
Esbozar una gráfica de:\(f(x) = \log (x)\),\(g(x) = \ln (x)\)
Encuentra el dominio de cada función.
| 30. \(f(x) = \log (x-5)\) | 31. \(f(x) = \ln (3-x)\) |
| 32. \(f(x) = \ln (1-3x)\) | 33. \(f(x) = \log (2x+5)\) |


