1.3: Funciones lineales
- Page ID
- 110592
A medida que te subes a un taxi en Allentown, el medidor leerá inmediatamente $3.30; esta es la carga de “caída” que se realiza cuando se activa el taxímetro. Después de esa tarifa inicial, el taxímetro agregará $2.40 por cada milla que conduzca el taxi. En este escenario, la tarifa total del taxi depende del número de millas recorridas en el taxi, y podemos preguntar si es posible modelar este tipo de escenarios con una función. Usando variables descriptivas, elegimos\(m\) para millas y\(C\) para Costo en dólares en función de millas:\(C(m)\).
Sabemos con certeza que\(C(0)=3.30\), ya que el cargo por caída de $3.30 se evalúa independientemente de cuántas millas se conduzcan. Dado que se agregan $2.40 por cada milla conducida, podríamos escribir que si se manejan\(m\) millas,\(C(m)=3.30+2.40m\) porque comenzamos con una tarifa de caída de $3.30 y luego por cada aumento de milla agregamos $2.40.
Es bueno verificar que las unidades tengan sentido en esta ecuación. El cargo por caída de $3.30 se mide en dólares; el cargo de $2.40 se mide en dólares por milla. Entonces,\[C(m)=3.30\text{ dollars}+\left(2.40\frac{\text{dollars}}{\text{mile}}\right) (m\text{ miles})\nonumber \] cuando los dólares por milla se multiplican por un número de millas, el resultado es un número de dólares, igualando las unidades en las 3.30, y haciendo coincidir las unidades deseadas para la\(C\) función.
Observe que esta ecuación\(C(m)=3.30+2.40m\) consistió en dos cantidades. El primero es el cargo fijo de $3.30 que no cambia con base en el valor de la entrada. El segundo es el valor de $2.40 dólares por milla, que es una tasa de cambio. En la ecuación esta tasa de cambio se multiplica por el valor de entrada.
Al observar este mismo problema en formato de tabla también podemos ver los cambios de costos en $2.40 por cada aumento de 1 milla:
| \(m\) | 0 | 1 | 2 | 3 |
| \(C(m)\) | 3.30 | 5.70 | 8.10 | 10.50 |
Aquí es importante señalar que en esta ecuación, la tasa de cambio es constante; en cualquier intervalo, la tasa de cambio es la misma.
Graficando esta ecuación,\(C(m)=3.30+2.40m\) vemos que la forma es una línea, que es como estas funciones obtienen su nombre: funciones lineales.
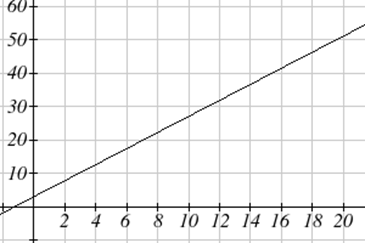
Cuando el número de millas es cero el costo es de $3.30, dando el punto (0, 3.30) en la gráfica. Esta es la vertical o\(C(m)\) intercepción. El gráfico está aumentando en línea recta de izquierda a derecha porque por cada milla el costo sube $2.40; esta tasa sigue siendo consistente.
Una función lineal es una función cuya gráfica produce una línea. Las funciones lineales siempre se pueden escribir en la forma\[f(x)=b+mx\nonumber \] o\[f(x)=mx+b\nonumber \] donde\(b\) está el valor inicial o inicial de la función (con entrada\(x = 0\)), y\(m\) es la tasa constante de cambio de la función.
Esta forma de una línea se llama forma pendiente-intercepción de una línea.
A muchas personas les gusta escribir funciones lineales en la forma\(f(x)=b+mx\) porque corresponde a la forma en que tendemos a hablar: “La salida comienza en\(b\) y aumenta a un ritmo de”\(m\).
Solo por esta razón usaremos el\(f(x)=b+mx\) formulario para muchos de los ejemplos, pero recuerda que son equivalentes y se pueden escribir correctamente en ambos sentidos. [Si bien esta es la convención del libro, en clase y en los videos probablemente usaré\(f(x)=mx+b\).]
\(m\)es la tasa constante de cambio de la función (también llamada pendiente). La pendiente determina si la función es una función creciente o una función decreciente.
- \(f(x)=b+mx\)es una función creciente si\(m\gt 0\).
- \(f(x)=b+mx\)es una función decreciente si\(m\lt 0\).
Si\(m=0\), la tasa de cambio es 0, y la función\(f(x)=b+0x=b\) es solo una línea horizontal que pasa por el punto (0, b), sin aumentar ni disminuir.
Actualmente Marcus posee 200 canciones en su colección de iTunes. Cada mes, agrega 15 canciones nuevas. Escribir una fórmula para el número de canciones,\(N\), en su colección de iTunes en función del número de meses,\(m\). ¿Cuántas canciones tendrá en un año?
Solución
El valor inicial para esta función es de 200, ya que actualmente posee 200 canciones, entonces\(N(0)=200\). El número de canciones aumenta en 15 canciones al mes, por lo que la tasa de cambio es de 15 canciones al mes. Con esta información, podemos escribir la fórmula:\[N(m)=200+15m.\nonumber \]
\(N(m)\)es una función lineal creciente.
Con esta fórmula podemos predecir cuántas canciones tendrá en 1 año (12 meses):\[N(12)=200+15(12)=200+180=380.\nonumber \] Marcus tendrá 380 canciones en 12 meses.
Dados dos valores para la entrada\( x_2 \),\( x_1 \) y, y dos valores correspondientes para la salida\( y_2 \),\( y_1 \) y, o un conjunto de puntos\( (x_2,y_2) \),\( (x_1,y_1) \) y, si deseamos encontrar una función lineal que contenga ambos puntos podemos calcular la tasa de cambio,\(m\):\[m=\dfrac{\text{change in output}}{\text{change in input}}=\dfrac{\Delta y}{\Delta x}=\dfrac{y_2-y_1}{x_2-x_1}.\nonumber \]
La tasa de cambio de una función lineal también se llama la pendiente de la línea.
Nota en notación de funciones\(y_2=f(x_2)\),\(y_1=f(x_1)\) y, así podríamos escribir equivalentemente\[m=\dfrac{f(x_2)-f(x_1)}{x_2-x_1}.\nonumber \]
La población de una ciudad aumentó de 23,400 a 27,800 entre 2002 y 2006. Encuentra la tasa de cambio de la población durante este lapso de tiempo.
Solución
La tasa de cambio relacionará el cambio en la población con el cambio en el tiempo. La población aumentó en 27800-23400=4400 personas en el intervalo de tiempo de 4 años. Para encontrar la tasa de cambio, el número de personas por año la población cambió por:\[\dfrac{4400 \text{ people}}{4\text{ years}}=1100\dfrac{\text{people}}{\text{year}}=1100 \text{ people per year}.\nonumber \]
Observe que sabíamos que la población iba en aumento, por lo que esperaríamos\(m\) que nuestro valor fuera positivo. Esta es una forma rápida de verificar si tu valor es razonable.
La presión,\(P\), en libras por pulgada cuadrada (PSI) sobre un buceador depende de su profundidad por debajo de la superficie del agua\(d\),, en pies, siguiendo la ecuación\(P(d)=14.696+0.43d\). Interpretar los componentes de esta función.
Solución
La tasa de cambio, o pendiente, 0.434 tendría unidades\(\dfrac{\text{output}}{\text{input}}=\dfrac{\text{pressure}}{\text{depth}}=\dfrac{\text{PSI}}{\text{ft}}\). Esto nos dice que la presión sobre el buceador aumenta en 0.434 PSI por cada pie aumenta su profundidad.
El valor inicial, 14.696, tendrá las mismas unidades que la salida, por lo que esto nos dice que a una profundidad de 0 pies, la presión sobre el buceador será de 14.696 PSI.
Ahora podemos encontrar la tasa de cambio dada dos pares entrada-salida, y podríamos escribir una ecuación para una función lineal si tuviéramos la tasa de cambio y el valor inicial. Si tenemos dos pares entrada-salida y no incluyen el valor inicial de la función, entonces tendremos que resolverlo.
Escribe una ecuación para la función lineal graficada a continuación.
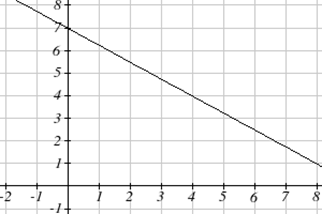
Solución
Al mirar la gráfica, podríamos notar que pasa por los puntos (0, 7) y (4, 4). Desde el primer valor, sabemos que el valor inicial de la función es\(b = 7\), por lo que en este caso solo necesitaremos calcular la tasa de cambio:\[m=\dfrac{4-7}{4-0}=\dfrac{-3}{4}\nonumber \]
Esto nos permite escribir la ecuación:\[f(x)=7-\frac{3}{4}x\nonumber \]
Si\(f(x)\) es una función lineal,\(f(3)=-2\), y\(f(8)=1\), encontrar una ecuación para la función.
Solución
En Ejemplo\(\PageIndex{3}\), calculamos la tasa de cambio a ser\(m=\frac{3}{5}\). En este caso, desconocemos el valor inicial\(f(0)\), por lo que tendremos que resolverlo. Usando la tasa de cambio, sabemos que la ecuación tendrá la forma\(f(x)=b+\frac{3}{5}x\). Ya que conocemos el valor de la función cuando\(x = 3\), podemos evaluar la función en 3:\(f(x)=b+\frac{3}{5}(3)\).
Ya que sabemos eso\(f(3)=-2\), podemos sustituir por el lado izquierdo:\(-2=b+\frac{3}{5}(3)\).
Esto nos deja con una ecuación que podemos resolver para el valor inicial:\(b=-2-\frac{9}{5}=-\frac{19}{5}\).
Combinando esto con el valor de la tasa de cambio, ahora podemos escribir una fórmula para esta función:\[f(x)=-\frac{19}{5}+\frac{3}{5}x.\nonumber \]
Como alternativa al enfoque utilizado anteriormente para encontrar el valor inicial, b, podemos usar la forma punto-pendiente de una línea en su lugar.
Una ecuación para la línea que pasa por el punto\((x_1, y_1)\) con pendiente se\(m\) puede escribir como\[y-y_1=m(x-x_1)\nonumber \]
Esto se llama la forma punto-pendiente de una línea. Es un poco más fácil escribir si conoces un punto y la pendiente, pero requiere un poco de trabajo para reescribir en forma de pendiente-intercepción, y requiere memorizar otra fórmula.
Al trabajar como vendedor de seguros, Ilya gana un salario base y una comisión por cada nueva póliza, por lo que el ingreso semanal de Ilya\(I\),, depende del número de pólizas nuevas, n, vende durante la semana. La semana pasada vendió 3 nuevas pólizas, y ganó 760 dólares por semana. La semana anterior, vendió 5 nuevas pólizas, y ganó $920. Encontrar una ecuación para\(I(n)\), e interpretar el significado de los componentes de la ecuación.
Solución
La información dada nos da dos pares entrada-salida: (3,760) y (5,920). Comenzamos por encontrar la tasa de cambio:\[m=\dfrac{920-760}{5-3}=\dfrac{160}{2}=80.\nonumber \]
Hacer un seguimiento de las unidades puede ayudarnos a interpretar esta cantidad. Los ingresos aumentaron 160 dólares cuando el número de pólizas aumentó en 2, por lo que la tasa de cambio es de 80 dólares por póliza; Ilya gana una comisión de 80 dólares por cada póliza vendida durante la semana.
Ahora podemos escribir la ecuación usando la forma punto-pendiente de la línea, usando la pendiente que acabamos de encontrar y el punto (3,760):\[I-760= 80(n-3)\nonumber \]
Si quisiéramos esto en forma de función (forma de intersección de pendiente), podríamos reescribir la ecuación en esa forma:\[\begin{align*} I-760 & = 80(n-3)\\ I-760 & = 80n-240\\ I(n) & = 520+80n \end{align*}\]
Esta forma nos permite ver el valor inicial de la función: 520. Este es el ingreso de Ilya cuando\(n = 0\), lo que significa que no se venden nuevas pólizas. Podemos interpretar esto como el salario base de Ilya para la semana, que no depende del número de pólizas vendidas.
Nuestra interpretación final es: el salario base de Ilya es de 520 dólares semanales y gana una comisión adicional de 80 dólares por cada póliza vendida cada semana.
Gráficas de Funciones Lineales
Gráficamente, en la ecuación\(f(x)=b+mx\),
- \(b\)es la intersección vertical de la gráfica y nos dice que podemos iniciar nuestra gráfica en\((0, b)\)
- y\(m\) es la pendiente de la línea y nos dice hasta qué punto subir y correr para llegar al siguiente punto.
Una vez que tengamos al menos 2 puntos, podremos extender la gráfica de la línea hacia la izquierda y la derecha.
Gráfica\(f(x)=5-\frac{2}{3}x\) usando la intersección vertical y pendiente.
Solución
La intersección vertical de la función es (0, 5), dándonos un punto en la gráfica de la línea. El desnivel es\(-\frac{2}{3}\). Esto nos dice que por cada 3 unidades la gráfica “corre” en la horizontal, la “subida” vertical disminuye en 2 unidades. Al graficar, podemos usar esto trazando primero nuestra intersección vertical en la gráfica, luego usando la pendiente para encontrar un segundo punto. A partir del valor inicial (0, 5) la pendiente nos dice que si nos movemos hacia la derecha 3, nos moveremos hacia abajo 2, moviéndonos al punto (3, 3). Podemos continuar esto nuevamente para encontrar un tercer punto en (6, 1). Por último, extender la línea hacia la izquierda y hacia la derecha, conteniendo estos puntos.
Otra opción para graficar es utilizar transformaciones de la función de identidad\(f(x)=x\). En la ecuación\(f(x)=mx\), el\(m\) está actuando como el estiramiento vertical de la función de identidad. Cuando\(m\) es negativo, también hay una reflexión vertical de la gráfica. Observar algunos ejemplos también ayudará a mostrar el efecto de la pendiente en la forma de la gráfica:
En\(f(x)=mx+b\), el\(b\) actúa como el desplazamiento vertical, moviendo la gráfica hacia arriba y hacia abajo sin afectar la pendiente de la línea. Algunos ejemplos:
Pruébalo tú mismo usando este applet:
Haga coincidir cada ecuación con una de las líneas de la gráfica a continuación\[\begin{align*} f(x) & = 2x+3\\ g(x) & = 2x-3\\ h(x) & = -2x+3\\ j(x) & = \frac{1}{2}x+3 \end{align*}\]
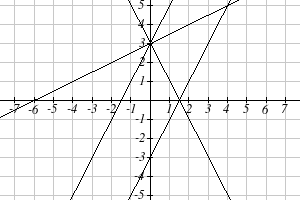
Solución
Sólo una gráfica tiene una intersección vertical de -3, por lo que podemos hacer coincidir inmediatamente esa gráfica con\(g(x)\). Para las tres gráficas con una intersección vertical a 3, solo una tiene pendiente negativa, por lo que podemos hacer coincidir esa línea con\(h(x)\). De las otras dos, la línea más pronunciada tendría una pendiente mayor, por lo que podemos hacer coincidir esa gráfica con la ecuación\(f(x)\), y la línea más plana con la ecuación\(j(x)\).
Además de comprender el comportamiento básico de una función lineal (creciente o decreciente, reconociendo la pendiente y la intersección vertical), a menudo es útil conocer la intercepción horizontal de la función —donde cruza el eje horizontal.
La intersección horizontal de la función es donde la gráfica cruza el eje horizontal. Si una función tiene una intercepción horizontal, siempre puedes encontrarla resolviendo\(f(x)=0\).
Encuentra la intersección horizontal de\(f(x)=-3+\frac{1}{2}x\)
Solución
Establecer la función igual a cero para encontrar qué entrada nos pondrá en el eje horizontal:\[\begin{align*} 0 & = -3+\frac{1}{2}x\\ 3 & = \frac{1}{2}x\\ x & = 6 \end{align*}\] Así la gráfica cruza el eje horizontal en (6,0).
Intersecciones de Líneas
Las gráficas de dos líneas se cruzarán si no son paralelas. Se cruzarán en el punto que satisfaga ambas ecuaciones. Para encontrar este punto cuando las ecuaciones se dan como funciones, podemos resolver para un valor de entrada para que\(f(x)=g(x)\). En otras palabras, podemos establecer las fórmulas para las líneas iguales, y resolver para la entrada que satisfaga la ecuación.
La economía nos dice que en un mercado libre, el precio de un artículo está relacionado con la cantidad que los productores van a suministrar y la cantidad que los consumidores van a exigir. Los aumentos en los precios disminuirán la demanda, mientras que la oferta tiende a aumentar con los precios. En ocasiones la oferta y la demanda se modelan con funciones lineales.
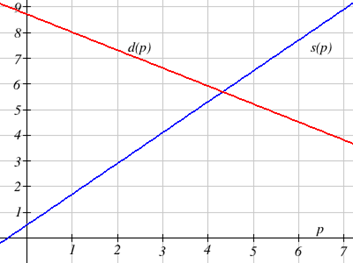
El suministro, en miles de artículos, para fundas de teléfono personalizadas se puede modelar por la ecuación\(s(p)=0.5+1.2p\) mientras que la demanda puede ser modelada por\(d(p)=8.7-0.7p\), donde\(p\) está en dólares. Encuentre el precio y la cantidad de equilibrio, la intersección de las curvas de oferta y demanda.
Solución
Ajuste\(s(p)=d(p)\), encontramos\[\begin{align*} 0.5+1.2p & = 8.7-0.7p\\ 1.9p & = 8.2\\ p & \approx \$4.32 \end{align*}\]
Podemos encontrar el valor de salida del punto de intersección evaluando cualquiera de las funciones en esta entrada:\[s(4.32)=0.5+1.2(4.32)\approx 5.68\nonumber \]
Estas líneas se cruzan en el punto (4.32, 5.68). Al mirar la gráfica, este resultado parece razonable.
Aplicaciones de negocios
En los negocios, una aplicación muy común de funciones es modelar el costo, los ingresos y las ganancias.
Cuando una empresa produce\(q\) artículos, el costo total es el costo del costo total de producción de esos artículos. El costo total incluye tanto los costos fijos, que son los costos iniciales, como equipos y edificios, como los costos variables, que son costos que dependen del número de artículos producidos, como materiales y mano de obra.
En el caso más simple, Costo Total = (Costos Fijos) + (Costos Variables)\(\bf \cdot \)\(\bf q\)
Los ingresos son la cantidad de dinero que una empresa aporta de las ventas.
En el caso más simple, Ingresos = (Precio por artículo)\(\bf \cdot \)\(\bf q\)
El beneficio es la cantidad de dinero que aporta, después de los gastos.
Beneficio = Ingresos — Costos
A menudo hablamos del punto de equilibrio. Este es el nivel de producción donde Ingresos equivale a Costo, o equivalentemente donde la Ganancia es cero. Este suele ser el nivel mínimo de ventas necesario para que la empresa obtenga ganancias.
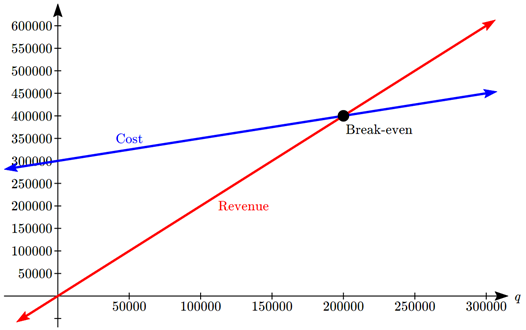
Una startup tecnológica está buscando desarrollar y lanzar una nueva aplicación móvil. El desarrollo inicial de la aplicación costará $300,000, y estiman que el marketing y el soporte para cada usuario costarán $0.50. Si bien la aplicación será gratuita, estiman que podrán traer $2 por usuario en promedio de las compras dentro de la aplicación. ¿Cuántos usuarios necesitará la empresa para alcanzar el punto de equilibrio?
Solución
Comenzamos modelando el costo, los ingresos y las ganancias. Let\(q\) = número de usuarios.
Los costos fijos (iniciales) son $300,000, y los costos variables (por artículo) como $0.50 por usuario. Podemos escribir la ecuación de costo total:
\(TC(q) = 300,000 + 0.50q\)
El ingreso será de $2 por usuario, por lo que la ecuación de ingresos será:
\(R(q) = 2q\)
Podríamos encontrar el punto de equilibrio estableciendo el costo total igual a los ingresos, lo que equivale a encontrar la intersección de las líneas.
Alternativamente, podríamos seguir adelante y encontrar una ecuación de ganancias primero:
\(P(q) = R(q) - TC(q) = 2q - (300,000+0.50q) = 1.5q - 300,000\)
El punto de equilibrio se puede encontrar estableciendo la ganancia igual a cero:\[\begin{align*} 0 & = 1.5q - 300,000\\ q & = 200,000 \end{align*}\]
La compañía tendrá que adquirir 200 mil usuarios para alcanzar el equilibrio.
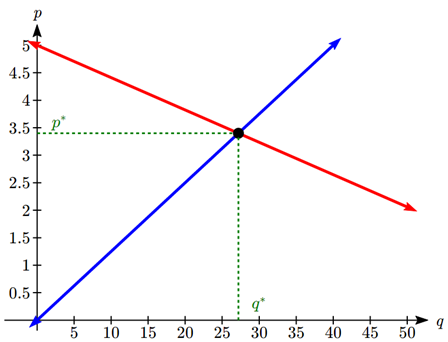
En economía, existe un modelo de cómo se determinan los precios en un mercado libre que establece que la oferta y la demanda de un producto están relacionadas con el precio. La relación de demanda muestra la cantidad de un determinado producto que los consumidores están dispuestos a comprar a un precio determinado. Normalmente la cantidad demandada disminuirá para un artículo si el precio aumenta. La relación de oferta muestra la cantidad de un producto que los proveedores están dispuestos a producir a un determinado precio de venta. Normalmente la oferta demandada aumentará si el precio aumenta. La teoría económica dice que la oferta y la demanda interactuarán, y la intersección será el precio de equilibrio, o precio de mercado, donde la cantidad suministrada y demandada será igual.
Si\(p\) es el precio de un producto, entonces
\(Q_d\)es la cantidad demandada
\(Q_s\)es la cantidad suministrada
La curva de demanda es una función decreciente, mientras que la curva de oferta es una función creciente.
La intersección de las curvas es el precio de equilibrio y la cantidad, también llamado precio de mercado y cantidad. Este punto suele señalarse como\(p^*\),\(Q^*\).
Posteriormente en el curso explorarás curvas de oferta y demanda que son no lineales, pero en esta sección nos centraremos en las funciones lineales de oferta y demanda.
En la mayoría de los libros económicos, verá la curva de oferta y demanda escrita con el precio como entrada y la cantidad como salida, como\(Q_d = 140 - 2p\). Sin embargo, las gráficas de oferta y demanda se dibujan con el precio en el eje vertical y la cantidad en el horizontal. Podemos escribir la ecuación de la manera que nos resulte más conveniente.
A un precio de $2.50 por galón, hay una demanda en cierto pueblo por 42.5 mil galones de gas y un suministro de 20 mil galones. A un precio de $3.50, hay demanda de 25.5 mil galones y una oferta de 28 mil galones. Suponiendo que la oferta y la demanda son lineales, encuentra el equilibrio precio y cantidad.
Solución
Comenzamos por encontrar una ecuación lineal tanto para la oferta como para la demanda. Utilizaremos precio,\(p\) en dólares, como salida y cantidad,\(q\) en miles de galones, como insumo.
Para el suministro, tenemos los puntos (20, 2.50) y (28, 3.50).
Encontrar la pendiente:\(m = \dfrac{3.50-2.50}{28-20} = \frac{1}{8}\)
Sabemos que la ecuación se verá así\(p = \frac{1}{8}q+b\), sustituyendo en (20, 2.50)\[\begin{align*} 2.5 & = \frac{1}{8}(20) +b \\ 2.5 & = 2.5 +b \\ q & = 0 \end{align*}\]
La ecuación de la oferta es:\(p = \frac{1}{8}q\)
Por demanda, tenemos los puntos (42.5, 2.50) y (25.5, 3.50). Usando un enfoque similar, podemos encontrar la ecuación de demanda es:\(p = -\frac{1}{17}q+5\)
Para encontrar el equilibrio, establecemos la oferta igual a la demanda:
\(\frac{1}{8}q = -\frac{1}{17}q+5\)
Multiplicando por 8 (17) = 136 para borrar las fracciones,
\(136\left(\frac{1}{8}q\right) = 136\left(-\frac{1}{17}q+5\right)\)
\(17q = -8q+680\)
Ahora resolvemos para\(q\)
\(25q = 680\)
\(q = 27.2\)
Para encontrar el precio de equilibrio, podemos sustituir ese valor de nuevo en cualquiera de las ecuaciones:
\(p = \frac{1}{8}(27.2) = 3.4\)
La cantidad de equilibrio será de 27.2 mil galones de gas a un precio de $3.40.
