2.2: Gráficas de Funciones Lineales

Última actualización
Guardar como PDF

Page ID: 116750

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Cuando estamos trabajando con una nueva función, es útil saber todo lo que podamos sobre la función: su grafo, donde la función es cero, y cualquier otro comportamiento especial de la función. Comenzaremos esta exploración de funciones lineales con una mirada a las gráficas.

Al graficar una función lineal, hay tres formas básicas de graficarla:

Trazando puntos (al menos 2) y dibujando una línea a través de los puntos
Usando el valor inicial (salida cuando x = 0) y la tasa de cambio (pendiente)
Uso de transformaciones de la función de identidad$f(x)=x$

Ejemplo$\PageIndex{1}$

$f(x)=5-\dfrac{2}{3} x$Gráfica trazando puntos.

Solución

En general, evaluamos la función en dos o más entradas para encontrar al menos dos puntos en la gráfica. Por lo general, lo mejor es elegir valores de entrada que “funcionen bien” en la ecuación. En esta ecuación, los múltiplos de 3 funcionarán muy bien debido a lo$\dfrac{2}{3}$ en la ecuación, y por supuesto$x = 0$ usándolos para obtener la intercepción vertical. Evaluando$f(x)$ en$x = 0$, 3 y 6: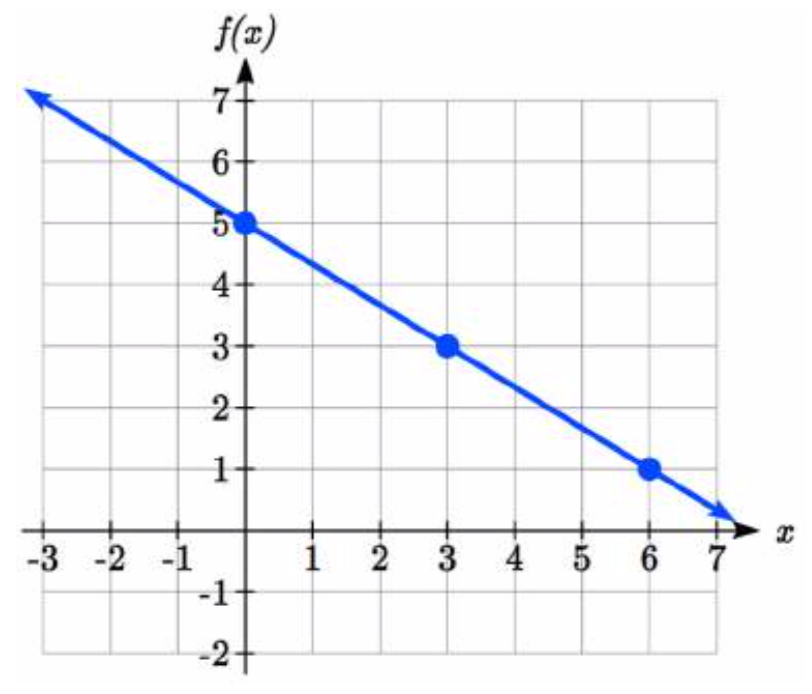 $Una línea decreciente con puntos marcados en la línea en 0 coma 5, 3 coma 3 y 6 coma 1$

\[f(0) = 5 - \dfrac{2}{3} (0) = 5\nonumber \]

\[f(3) = 5 - \dfrac{2}{3} (3) = 3\nonumber \]

\[f(6) = 5 - \dfrac{2}{3} (6) = 1\nonumber \]

Estas evaluaciones nos dicen que los puntos (0,5), (3,3) y (6,1) se encuentran en la gráfica de la línea. Trazar estos puntos y trazar una línea a través de ellos nos da la gráfica.

Al usar el valor inicial y la tasa de cambio para graficar, debemos considerar la interpretación gráfica de estos valores. Recuerde que el valor inicial de la función es la salida cuando la entrada es cero, por lo que en la ecuación$f(x)=b+mx$, la gráfica incluye el punto$(0, b)$. En la gráfica, esta es la intersección vertical, el punto donde la gráfica cruza el eje vertical. 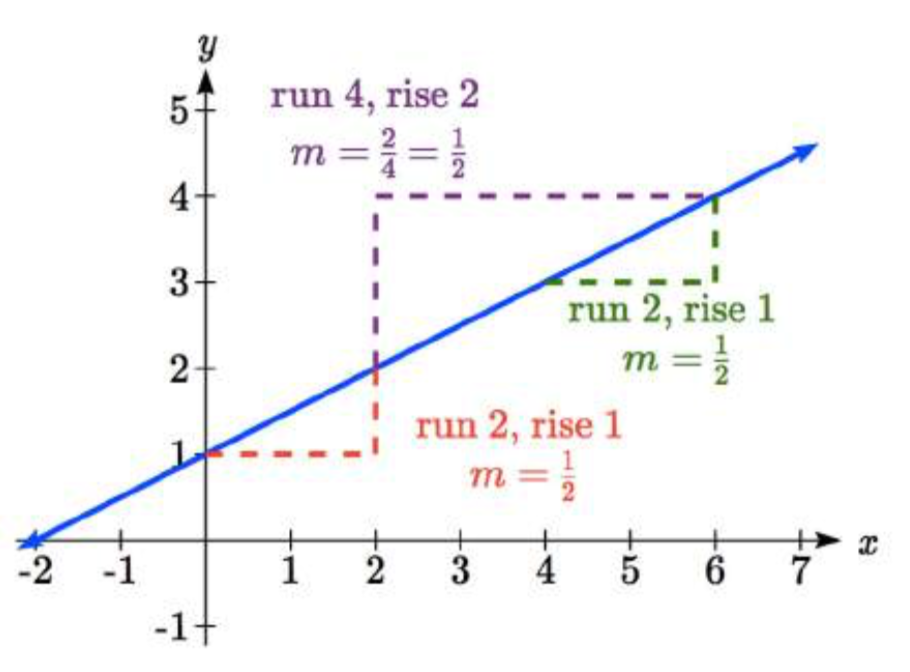$Una línea creciente que pasa por 0 coma 1 y 2 coma 2 con un triángulo dibujado etiquetado como carrera 2, subida 1, m=mitad. Otro triángulo de 2 coma 2 a 6 coma 4 etiquetada carrera 4, subida 2, m=dos cuartas partes = una mitad. Un tercer triángulo de 4 coma 3 a 6 coma 4 con un triángulo dibujado etiquetado como carrera 2, subida 1, m=mitad.$

Para la tasa de cambio, es útil recordar que calculamos este valor como

\[m = \dfrac{change\ of\ output}{change\ of\ input}\nonumber\]

A partir de una gráfica de una línea, esto nos dice que si dividimos la diferencia vertical, o subida, de las salidas de la función por la diferencia horizontal, o corrida, de las entradas, obtendremos la tasa de cambio, también llamada pendiente de la línea.

\[m=\dfrac{change\ of \ output}{change\ of\ input} = \dfrac{rise}{run}\nonumber \]

Observe que esta relación es la misma independientemente de qué dos puntos usemos.

Definición: Interpretación gráfica de una ecuación lineal

Gráficamente, en la ecuación$f(x)=b+mx$,

$b$es la intersección vertical de la gráfica y nos dice que podemos iniciar nuestra gráfica en (0, b)

$m$es la pendiente de la línea y nos dice hasta qué punto subir y correr para llegar al siguiente punto

Una vez que tengamos al menos 2 puntos, podremos extender la gráfica de la línea hacia la izquierda y la derecha.

Ejemplo$\PageIndex{2}$

Gráfica$f(x)=5-\dfrac{2}{3} x$ usando la intersección vertical y pendiente.

Solución

El intercepto vertical de la función es (0, 5), dándonos un punto en la gráfica de la línea.

La pendiente es$-\dfrac{2}{3}$. Esto nos dice que por cada 3 unidades la gráfica “corre” en la horizontal, la “subida” vertical disminuye en 2 unidades. 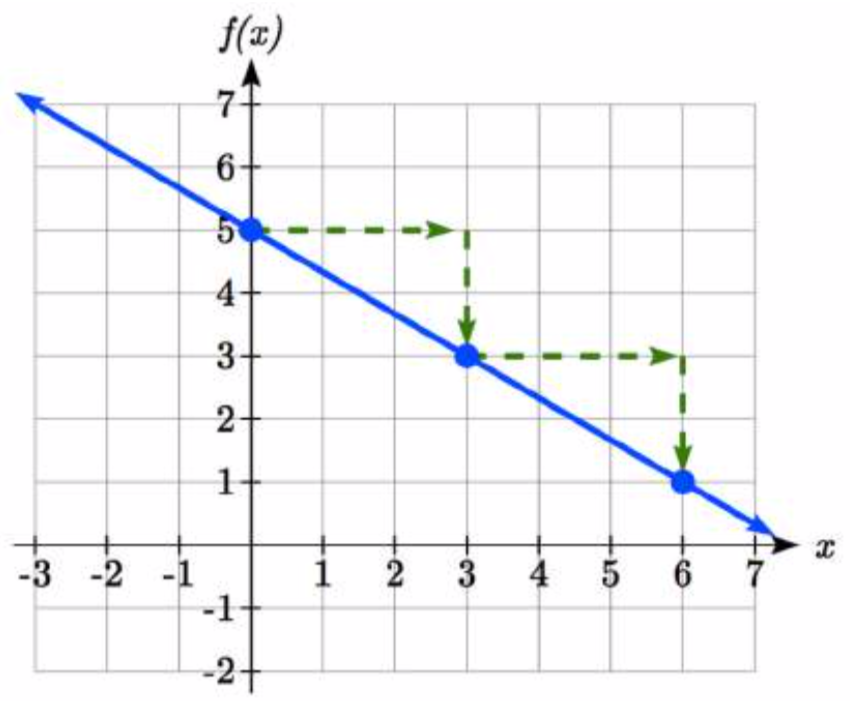$Una línea decreciente. Desde un punto en la línea en 0 coma 5 se dibuja una flecha apuntando 3 a la derecha, luego desde el final de esa otra flecha apuntando hacia abajo 2, terminando en el punto 3 coma 3 en la línea. A partir de ahí, se dibuja otra flecha apuntando 3 a la derecha luego otra 2 hacia abajo terminando en el punto 6 coma 1 en la línea.$

Al graficar, podemos usar esto trazando primero nuestra intersección vertical en la gráfica, luego usando la pendiente para encontrar un segundo punto. A partir del valor inicial (0, 5) la pendiente nos dice que si nos movemos hacia la derecha 3, nos moveremos hacia abajo 2, moviéndonos al punto (3, 3). Podemos continuar esto nuevamente para encontrar un tercer punto en (6, 1). Por último, extender la línea hacia la izquierda y hacia la derecha, conteniendo estos puntos.

Ejercicio$\PageIndex{1}$

Considera que la pendiente también$-\dfrac{2}{3}$ podría escribirse como$\dfrac{2}{-3}$. Utilizando$\dfrac{2}{-3}$, encuentra otro punto en la gráfica que tenga un$x$ valor negativo.

Responder: $(-3,7)$encontrado iniciando en la intersección vertical, subiendo$2$ unidades y$3$ en la dirección horizontal negativa. También podrías haber respondido,$(-6, 9)$ o$(-9, 11)$ etc...

Otra opción para graficar es utilizar transformaciones de la función de identidad$f(x)=x$.

En la ecuación$f(x)=mx$, la m está actuando como el estiramiento vertical de la función de identidad. Cuando$m$ es negativo, también hay una reflexión vertical de la gráfica. Mirando algunos ejemplos:

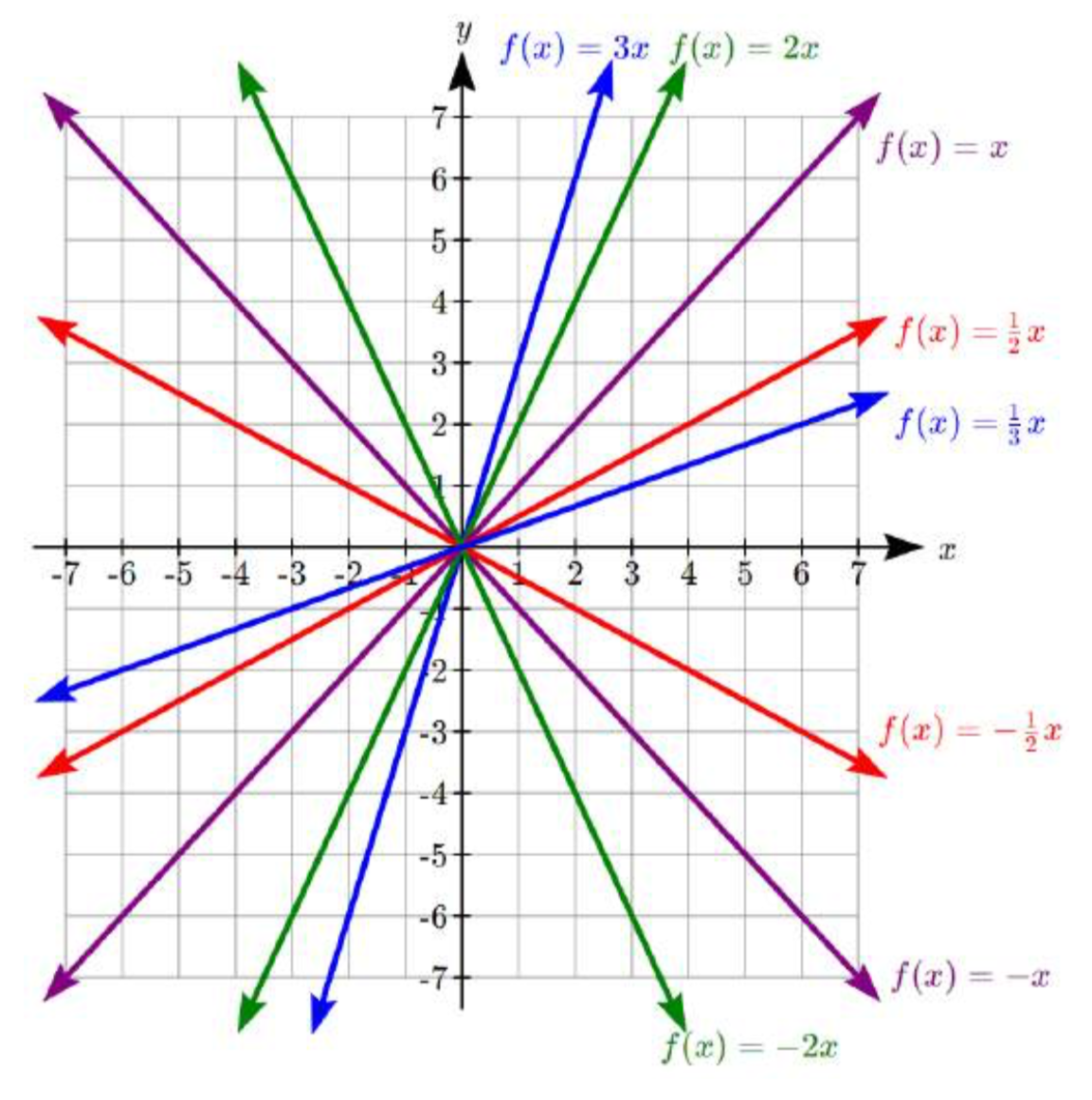
$Múltiples líneas etiquetadas en una gráfica, todas pasando por el origen. f (x) =un tercio x, pasando por 3 comas 1. f (x) =media x, pasando por 2 comas 1. f (x) =x, pasando por 1 coma 1. f (x) =2x pasando por 1 coma 2. f (x) =3x pasando por 1 coma 3.$

En$f(x)=mx+b$, el b actúa como el desplazamiento vertical, moviendo la gráfica hacia arriba y hacia abajo sin afectar la pendiente de la línea. Algunos ejemplos:

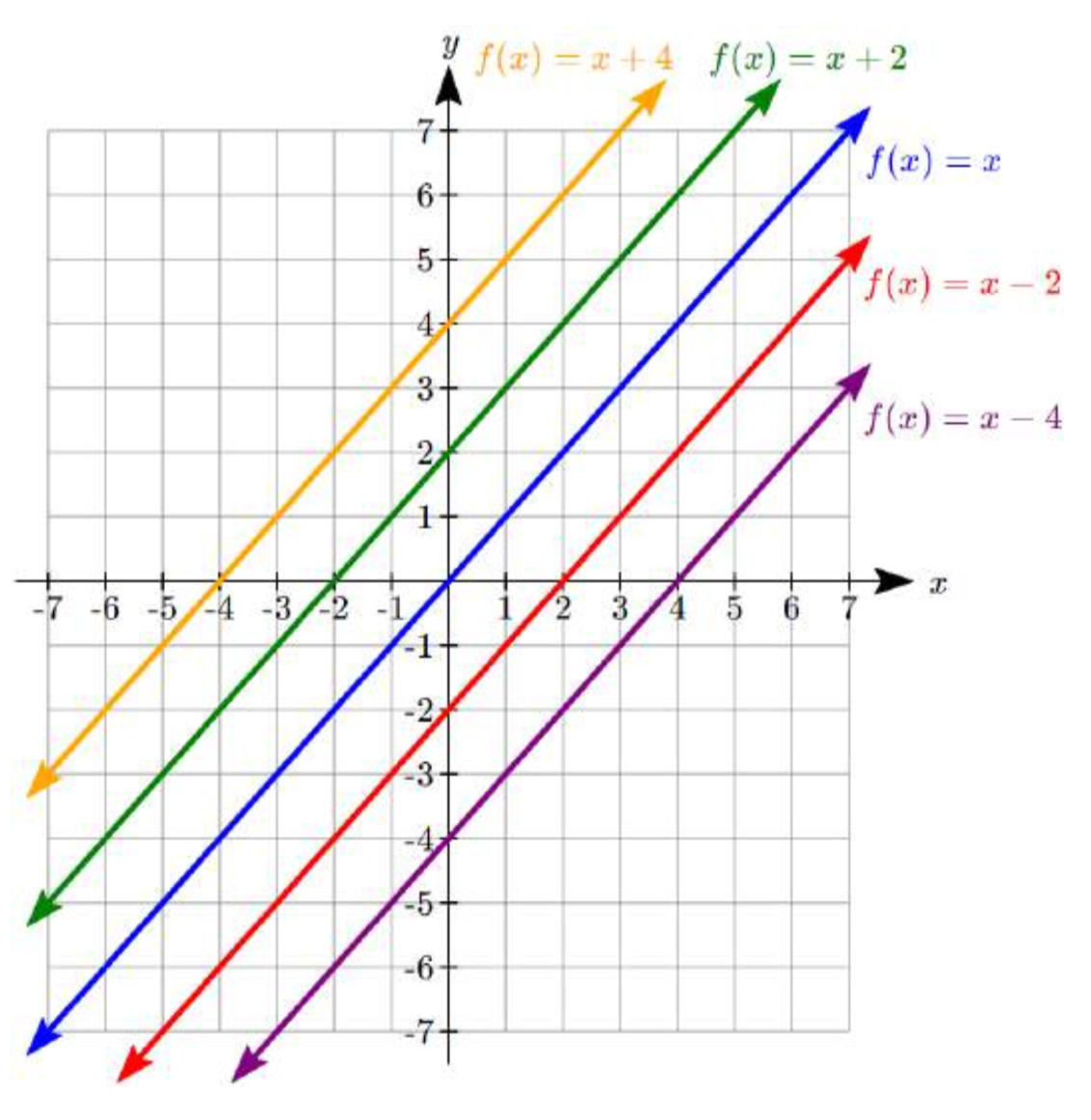
$Múltiples líneas etiquetadas en una gráfica, todas paralelas con la misma pendiente. f (x) =x pasando por 0 coma 0 y 2 coma 2. f (x) =xnegativo 2 pasando por 0 coma negativo 2 y 2 coma 0. f (x) =xnegativo 4 pasando por 0 coma negativa 4 y 2 coma negativa 2. f (x) =x+2 pasando por 0 coma 2 y 2 coma f (4. x) =x+4 pasando por 0 coma 4 y 2 coma 6$

Usar Estiramientos Verticales o Compresiones junto con Desplazamientos Verticales es otra manera de ver la identificación de diferentes tipos de funciones lineales. Aunque esta puede no ser la forma más fácil de graficar este tipo de función, asegúrate de practicar cada método.

Ejemplo$\PageIndex{3}$

Gráfica$f(x)=-3+\dfrac{1}{2} x$ usando transformaciones.

Solución

La ecuación es la gráfica de la función de identidad comprimida verticalmente por ½ y desplazada verticalmente hacia abajo 3.

Compresión vertical combinada con desplazamiento vertical

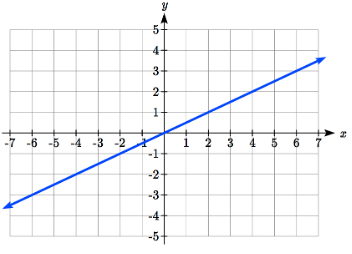
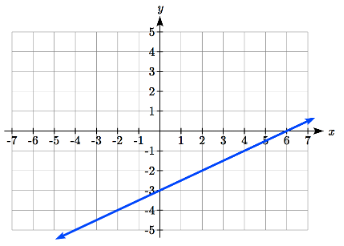
$clipboard_e95058ed4b067f942eaa437cd5390a4fd.png$ $clipboard_e7031802fc7b86d0dc9f7ffbbf6c0daf8.png$

Observe cómo esto se compara muy bien con el otro método donde se encuentra la intercepción vertical en (0, -3) y para llegar a otro punto nos elevamos (subimos verticalmente) por 1 unidad y corremos (vamos horizontalmente) por 2 unidades para llegar al siguiente punto (2, -2), y al siguiente (4, -1). En estos tres puntos (0, -3), (2, -2) y (4, -1), los valores de salida cambian en +1, y los$x$ valores cambian en +2, correspondientes a la pendiente$m = 1/2$.

Ejemplo$\PageIndex{4}$

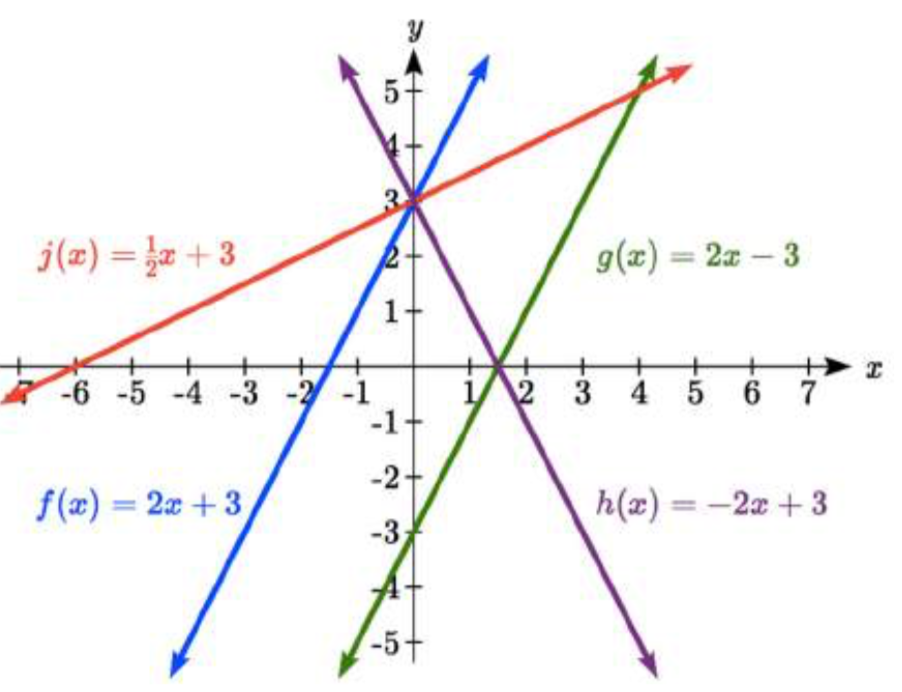
Coincidir cada ecuación con una de las líneas en la gráfica de abajo

\[f(x) = 2x + 3\nonumber \]

\[g(x) = 2x - 3\nonumber \]

\[(h(x) = -2x = 3\nonumber \]

\[j(x) = \dfrac{1}{2} x + 3\nonumber \]

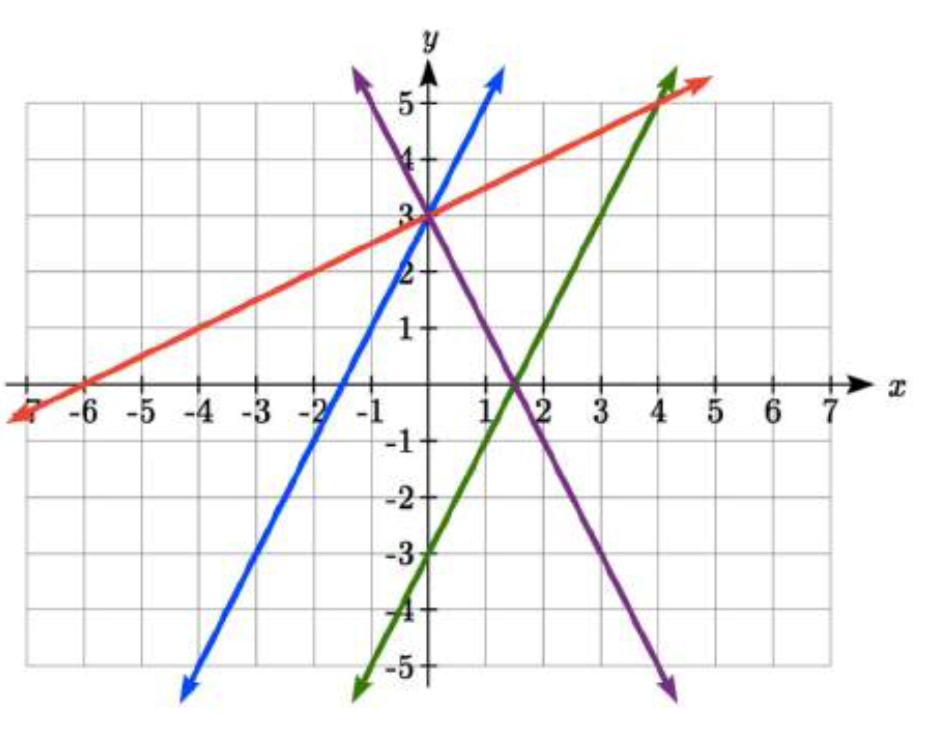
$Una línea roja a través de 0 coma 3 y 2 coma 4. Una línea azul pasando por 0 coma 3 y 1 coma 5. Una línea púrpura a través de 0 coma 3 y 1 coma 1. Una línea verde a través de 0 coma negativa 3 y 1 coma negativa 1.$

Solución

Sólo una gráfica tiene una intersección vertical de - 3, por lo que podemos hacer coincidir inmediatamente esa gráfica con$g(x)$.

Para las tres gráficas con una intersección vertical a 3, solo una tiene pendiente negativa, por lo que podemos hacer coincidir esa línea con$h(x)$. De las otras dos, la línea más pronunciada tendría una pendiente mayor, por lo que podemos hacer coincidir esa gráfica con la ecuación$f(x)$, y la línea más plana con la ecuación$j(x)$.

$Una línea roja a través de 0 coma 3 y 2 coma 4 etiquetada j (x) =1/2x+3. Una línea azul a través de 0 coma 3 y 1 coma 5 etiquetada con f (x) =2x+3. Una línea púrpura a través de 0 coma 3 y 1 coma 1 etiquetada h (x) =negativo 2x+3. Una línea verde a través de 0 coma negativa 3 y 1 coma negativa 1 etiquetada g (x) =2xnegativo 3$

Además de comprender el comportamiento básico de una función lineal (creciente o decreciente, reconociendo la pendiente y la intersección vertical), a menudo es útil conocer la intercepción horizontal de la función —donde cruza el eje horizontal.

Definición: Encontrar intercepciones horizontales

La intersección horizontal de la función es donde la gráfica cruza el eje horizontal. Si una función tiene una intercepción horizontal, siempre puedes encontrarla resolviendo$f(x) = 0$.

Ejemplo$\PageIndex{5}$

Encuentra la intersección horizontal de$f(x)=-3+\dfrac{1}{2} x$

Solución

Establecer la función igual a cero para encontrar qué entrada nos pondrá en el eje horizontal,

\[\begin{array} {rcl} {0} &= & {-3 + \dfrac{1}{2}x} \\ {3} &= & {\dfrac{1}{2} x} \\ {x} &= & {6} \end{array}\nonumber\]

La gráfica cruza el eje horizontal en (6,0)

Hay dos casos especiales de líneas: una línea horizontal y una vertical. En una línea horizontal como la gráfica a la derecha, observe que entre dos puntos cualesquiera, el cambio en las salidas es 0. En la ecuación de pendiente, el numerador será 0, resultando en una pendiente de 0. Usando una pendiente de 0 en el$f(x)=b+mx$, la ecuación simplifica a$f(x)=b$.

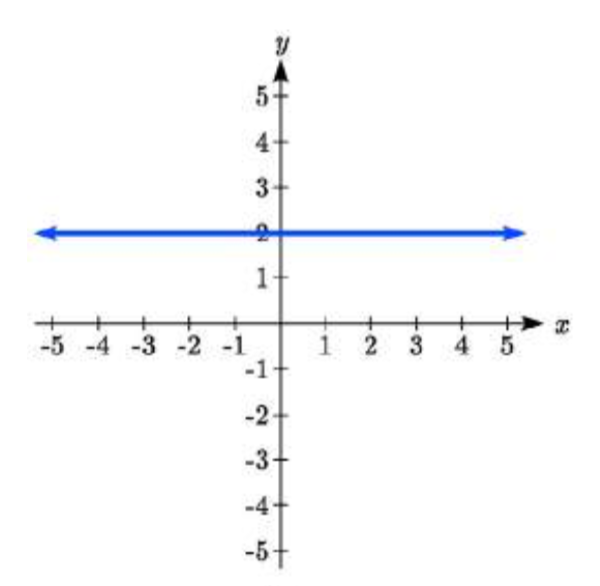
$Una línea horizontal que pasa por 0 coma 2 y 2 coma 2$

Observe que una línea horizontal tiene una intersección vertical, pero no una intersección horizontal (a menos que sea la línea$f(x) = 0$).

En el caso de una línea vertical, observe que entre dos puntos cualesquiera, el cambio en las entradas es cero. En la ecuación de pendiente, el denominador será cero, y tal vez recuerden que no podemos dividir por el cero; la pendiente de una línea vertical es indefinida. También puede notar que una línea vertical no es una función. Para escribir la ecuación de línea vertical, simplemente escribimos input=value, como$x = b$.

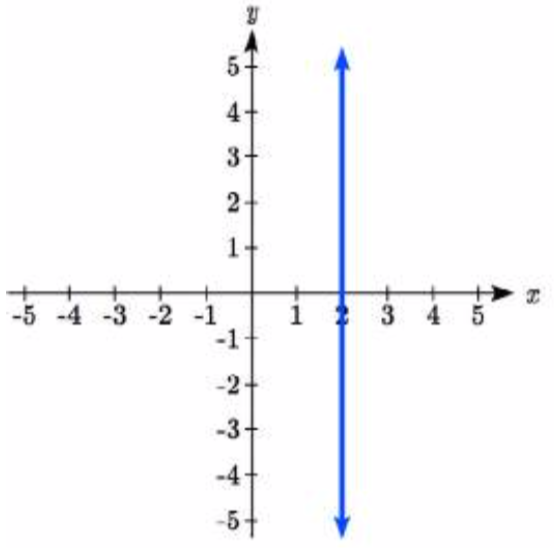
$Una línea vertical que pasa por 2 coma 0 y 2 coma 2$

Observe que una línea vertical tiene una intersección horizontal, pero no una intersección vertical (a menos que sea la línea$x = 0$).

Definición: líneas horizontales y verticales

Las líneas horizontales tienen ecuaciones de la forma$f(x)=b$

Las líneas verticales tienen ecuaciones de la forma$x = a$

Ejemplo$\PageIndex{6}$

Escribe una ecuación para la línea horizontal graficada arriba.

Solución

Esta línea tendría ecuación$f(x)=2$

Ejemplo$\PageIndex{7}$

Escribe una ecuación para la línea vertical graficada arriba.

Solución

Esta línea tendría ecuación$x=2$

Ejercicio$\PageIndex{2}$

Describir la función$f(x)=6-3x$ en términos de transformaciones de la función de identidad y encontrar su intercepción horizontal.

Responder

Estirado verticalmente por un factor de 3, Volteado verticalmente (volteado sobre el$x$ eje),

Desviado verticalmente hacia arriba en 6 unidades.

Intercepción horizontal:$6 - 3x = 0$ cuando$x=2$.

Líneas paralelas y perpendiculares

Cuando se grafican dos líneas juntas, las líneas serán paralelas si están aumentando a la misma velocidad —si las tasas de cambio son las mismas. En este caso, las gráficas nunca se cruzarán (a menos que sean la misma línea).

Definición: Líneas paralelas

Dos líneas son paralelas si las pendientes son iguales (o, si ambas líneas son verticales).

En otras palabras, dadas dos ecuaciones lineales$f(x)=b+m_{1} x$ y$g(x)=b+m_{2} x$, las líneas serán paralelas si$m_{1} =m_{2}$.

Ejemplo$\PageIndex{8}$

Encuentra una línea paralela a la$f(x)=6+3x$ que pasa por el punto (3, 0).

Solución

Sabemos que la línea que estamos buscando tendrá la misma pendiente que la línea dada,$m = 3$. Usando este y el punto dado, podemos resolver para la intercepción vertical de la nueva línea:

\[g(x) = b + 3x\nonumber\]luego en (3, 0),

\[0 = b + 3(3)\nonumber \]

\[b = -9\nonumber \]

La línea que estamos buscando es$g(x)=-9+3x$.

Si dos líneas no son paralelas, otra posibilidad interesante es que las líneas sean perpendiculares, lo que significa que las líneas forman un ángulo recto (ángulo de 90 grados — una esquina cuadrada) donde se encuentran. En este caso, las pendientes cuando se multipliquen juntas serán iguales a -1. Resolver por una pendiente nos lleva a la definición:

Definición: Líneas perpendiculares

Dadas dos ecuaciones lineales$f(x)=b+m_{1} x$ y$g(x)=b+m_{2} x$

Las líneas serán perpendiculares si$m_{1} m_{2} =-1$, y así$m_{2} =\dfrac{-1}{m_{1} }$

A menudo decimos que la pendiente de una línea perpendicular es el “recíproco negativo” de la pendiente de la otra línea.

Ejemplo$\PageIndex{9}$

Encuentra la pendiente de una línea perpendicular a una línea con:

a) una pendiente de 2. b) una pendiente de -4. c) una pendiente de$\dfrac{2}{3}$.

Solución

Si la línea original tuviera pendiente 2, la pendiente de la línea perpendicular sería$m_{2} =\dfrac{-1}{2}$

Si la línea original tuviera pendiente -4, la pendiente de la línea perpendicular sería$m_{2} =\dfrac{-1}{-4} =\dfrac{1}{4}$

Si la línea original tuviera pendiente$\dfrac{2}{3}$, la pendiente de la línea perpendicular sería$m_2 = \dfrac{-1}{2/3} = \dfrac{-3}{2}$

Ejemplo$\PageIndex{10}$

Encuentra la ecuación de una línea perpendicular$f(x)=6+3x$ y que pasa por el punto (3, 0).

Solución

La línea original tiene pendiente m = 3. La línea perpendicular tendrá pendiente$m=\dfrac{-1}{3}$. Usando este y el punto dado, podemos encontrar la ecuación para la línea.

\[g(x)=b-\dfrac{1}{3} x\nonumber \]luego en (3, 0),

\[0 = b - \dfrac{1}{3} (3)\nonumber \]

\[b = 1\nonumber \]

La línea que estamos buscando es$g(x)=1-\dfrac{1}{3} x$.

Ejercicio$\PageIndex{3}$

Dada la línea$h(t)=-4+2t$, encuentra una ecuación para la línea que pasa por (0, 0) que es:

paralelo a h (t).
perpendicular a h (t).

Responder

Paralelo:$f(t)=2t$

Perpendiculares:$g(t)=-\dfrac{1}{2} t$

Ejemplo$\PageIndex{12}$

Una línea pasa por los puntos (-2, 6) y (4, 5). Encuentra la ecuación de una línea perpendicular que pasa por el punto (4, 5).

Solución

A partir de los dos puntos dados en la línea de referencia, podemos calcular la pendiente de esa línea:

\[m_1 = \dfrac{5-6}{4 - (-2)} = \dfrac{-1}{6}\nonumber \]

La línea perpendicular tendrá pendiente

\[m_2 = \dfrac{-1}{-1/6} = 6\nonumber \]

Entonces podemos resolver para la intercepción vertical que hace que la línea pase por el punto deseado:

\[g(x) = b + 6x\nonumber \]luego en (4, 5)

\[5 = b + 6(4)\nonumber \]

\[b = -19\nonumber \]

Dando la línea$g(x)=-19+6x$

Intersecciones de Líneas

Las gráficas de dos líneas se cruzarán si no son paralelas. Se cruzarán en el punto que satisfaga ambas ecuaciones. Para encontrar este punto cuando las ecuaciones se dan como funciones, podemos resolver para un valor de entrada para que$f(x)=g(x)$. En otras palabras, podemos establecer las fórmulas para las líneas iguales, y resolver para la entrada que satisfaga la ecuación.

Ejemplo$\PageIndex{13}$

Encuentra la intersección de las líneas$h(t)=3t-4$ y$j(t)=5-t$.

Solución

Ajuste$h(t)=j(t)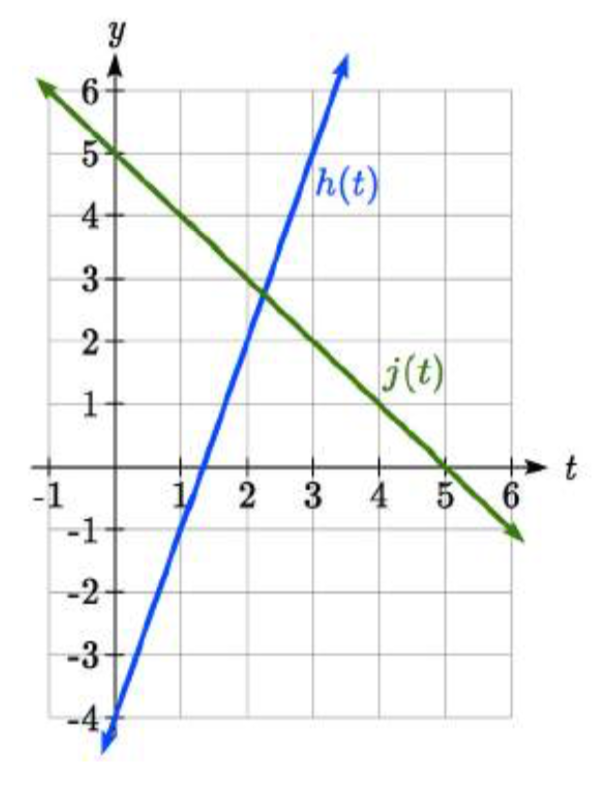$, $Una línea etiquetada h (t) que pasa por 0 coma negativa 4 y 2 coma 2, y una línea etiquetada j (t) que pasa por 0 coma 5 y 1 coma 4$

\[\begin{array} {rcl} {3t - 4} &= & {5 - t} \\ {4t} &= & {9} \\ {t} &= & {\dfrac{9}{4}} \end{array}\nonumber \]

Esto nos dice que las líneas se cruzan cuando la entrada es$\dfrac{9}{4}$.

Luego podemos encontrar el valor de salida del punto de intersección evaluando cualquiera de las funciones en esta entrada

\[j(\dfrac{9}{4} )=5-\dfrac{9}{4} =\dfrac{11}{4}\nonumber \]

Estas líneas se cruzan en el punto$(\dfrac{9}{4} ,\dfrac{11}{4} )$. Al mirar la gráfica, este resultado parece razonable.

Dos líneas paralelas también pueden cruzarse si resultan ser la misma línea. En ese caso, se cruzan en cada punto de las líneas.

Ejercicio$\PageIndex{4}$

Mire la gráfica del ejemplo 13 anterior y responda lo siguiente para la función$h(t)$:

a. Coordenadas de intercepción vertical

b. Coordenadas horizontales de interceptación

c. Pendiente

d. Es$j(t)$ paralelo o perpendicular a$h(t)$ (o ninguno)

e. Es h (t) una función creciente o decreciente (o ninguna)

f. Escribir una descripción de transformación desde la función del kit de herramientas de identidad$f(x) = x$

Responder

4. Dado$h(t)=3t-4$

a. (0, -4)

b.$(\dfrac{4}{3} ,0)$

c. Pendiente 3

d. Ni paralelo ni perpendicular

e. Función creciente

f. dada la función de identidad, estirar verticalmente 3 y desplazar hacia abajo 4 unidades.

Encontrar la intersección nos permite responder también a otras preguntas, como descubrir cuándo una función es más grande que otra.

Ejemplo$\PageIndex{14}$

Usando las funciones del ejemplo anterior, para qué valores de t es$h(t) > j(t)$.

Solución

Para responder a esta pregunta, es útil primero saber dónde son iguales las funciones, ya que ese es el punto donde$h(t)$ podría pasar de ser mayor a menor que$j(t)$ o viceversa. Del ejemplo anterior, sabemos que las funciones son iguales en$t=\dfrac{9}{4}$.

Al examinar la gráfica, podemos ver que$h(t)$, la función con pendiente positiva, va a ser mayor que la otra función a la derecha de la intersección. Así que$h(t) > j(t)$ cuando$t > \dfrac{9}{4}$

Temas Importantes de esta Sección

Métodos para graficar funciones lineales
Otro nombre para talud = elevar/correr
Intercepciones horizontales (a,0)
Líneas horizontales
Líneas verticales
Líneas paralelas
Líneas perpendiculares
Líneas de intersección