3.2: La Integral Definitiva
- Page ID
- 110498
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Distancia desde Velocity
Supongamos que un automóvil recorre una carretera recta a una velocidad constante de 40 millas por hora durante dos horas. Consulte la gráfica de su velocidad a continuación. ¿Hasta dónde ha llegado?
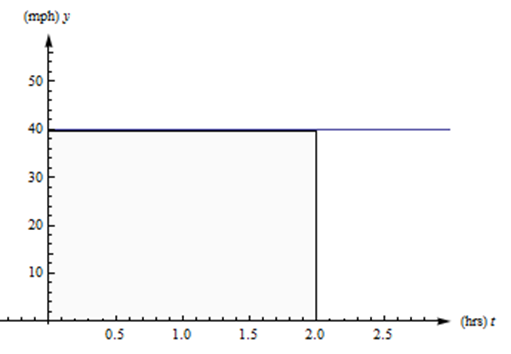
Solución
Todos recordamos distancia =\( \cdot \) tiempo de tasa, así que esta es fácil. El auto ha ido (40 millas/hora)\( \cdot \) (2 horas) = 80 millas.
Ahora supongamos que un automóvil viaja para que su velocidad aumente de manera constante de 0 a 40 millas por hora, durante dos horas. (Solo agradece que no estuvieras atrapado detrás de este auto en la autopista). Consulte la gráfica de su velocidad a continuación. ¿Hasta dónde ha llegado este auto?
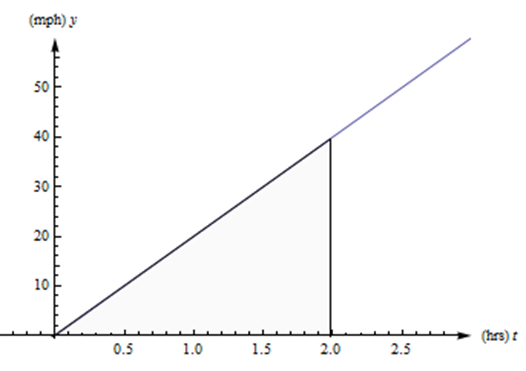
Solución
El problema con nuestra antigua relación confiable de distancia = tasa de\( \cdot \) tiempo es que solo funciona si la tasa es constante. Si la tarifa está cambiando, no hay una buena manera de usar esta fórmula.
Pero mira de nuevo la gráfica del último ejemplo. Observe que distancia = tasa de\( \cdot \) tiempo también describe el área entre el gráfico de velocidad y el\(t\) eje -eje, entre\(t = 0\) y\(t = 2\) horas. La tasa es la altura del rectángulo, el tiempo es la longitud del rectángulo y la distancia es el área del rectángulo. Esta es la forma en que podemos extender nuestra fórmula simple para manejar velocidades más complicadas: Y esta es la forma en que podemos responder al segundo ejemplo.
La distancia que recorre el automóvil es el área entre su gráfico de velocidad, el\(t\) eje\(t = 0\) -y\(t = 2\). Esta región es un triángulo, por lo que su área es\[\frac{1}{2}bh = \frac{1}{2}(2 \text{ hours})(40 \text{ miles per hour}) = 40 \text{ miles}.\nonumber \] Así que el automóvil recorre 40 millas durante su molesto viaje.
En nuestros ejemplos de distancia/velocidad, la función representó una tasa de desplazamiento (millas por hora), y el área representó la distancia total recorrida. Este principio funciona de manera más general:
Para funciones que representan otras tasas como la producción de una fábrica (bicicletas por día), o el flujo de agua en un río (galones por minuto) o el tráfico sobre un puente (automóviles por minuto), o la propagación de una enfermedad (personas recién enfermas por semana), el área seguirá representando el total cantidad de algo.
La gráfica a continuación muestra el caudal (pies cúbicos por segundo) de agua en el río Skykomish en la localidad de Goldbar en el estado de Washington.
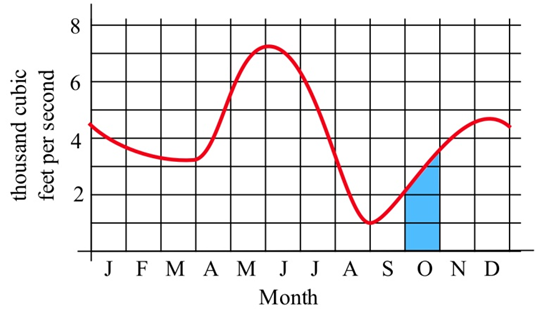
Solución
El área de la región sombreada representa el volumen total (pies cúbicos o\( \text{ft}^3 \)) de agua que fluye más allá de la localidad durante el mes de octubre. Podemos aproximar esta área para aproximar el agua total pensando en la región sombreada como un rectángulo con un triángulo en la parte superior.
\[ \begin{align*} \text{Total water } & = \text{ total area}\\ & \approx \text{ area of rectangle }+\text{ area of the "triangle"} \\ & \approx \left(2000 \frac{\text{ft}^3}{\text{s}}\right)\left(30 \text{ days}\right)+\frac{1}{2}\left(1500\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \\ & = \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \end{align*} \nonumber \]
Tenga en cuenta que necesitamos convertir las unidades para dar sentido a nuestro resultado:\[ \begin{align*} \text{Total water } & \approx \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(30\text{ days}\right) \\ & = \left(2570\frac{\text{ft}^3}{\text{s}}\right)\left(2,\!592,\!000\text{ sec}\right) \\ & \approx 7.128\cdot 10^9\text{ ft}^3 \end{align*} \nonumber \]
Alrededor de 7 mil millones de pies cúbicos de agua fluyeron más allá de Goldbar en octubre.
Aproximación con Rectángulos
¿Cómo aproximamos el área si la curva de tasa es, bueno, curvilínea
? Podríamos usar rectángulos y triángulos, como hicimos en el último ejemplo. Pero resulta ser más útil (y más fácil) simplemente usar rectángulos. Cuantos más rectángulos usemos, mejor será nuestra aproximación.
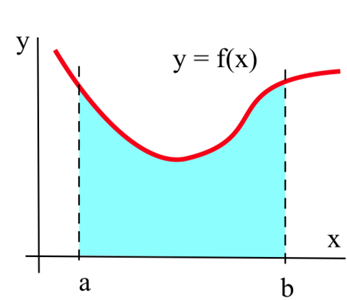
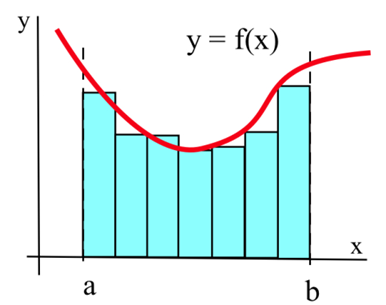
Supongamos que queremos calcular el área entre la gráfica de una función positiva\(f\) y el\(x\) eje -en el intervalo\([a, b]\) (graficado arriba). El método Riemann Sum consiste en construir varios rectángulos con bases en el intervalo\([a, b]\) y lados que alcanzan hasta la gráfica de\(f\) (ver abajo). Entonces las áreas de los rectángulos se pueden calcular y sumar juntas para obtener un número llamado Riemann Suma de\(f\) on\([a, b]\). El área de la región formada por los rectángulos es una aproximación del área que queremos.
Aproximar el área en la gráfica de la izquierda entre la gráfica de\(f\) y el\(x\) eje -en el intervalo [2, 5] sumando las áreas de los rectángulos en la gráfica de la derecha.
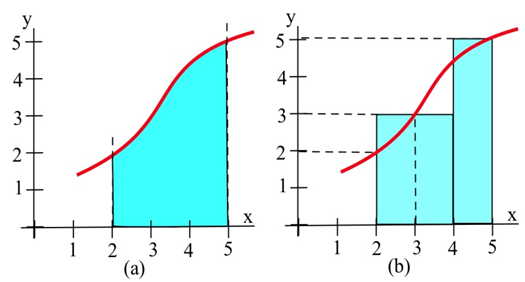
Solución
El área total de rectángulos es\[(2)(3) + (1)(5) = 11\text{ units}^2.\nonumber \]
\(A\)Sea la región delimitada por la gráfica de\(f(x) = \frac{1}{x}\), el\(x\) eje -y las líneas verticales en\(x = 1\) y\(x = 5\). No podemos encontrar exactamente el área (con lo que sabemos ahora), pero podemos aproximarla usando rectángulos.
Cuando hacemos nuestros rectángulos, tenemos muchas opciones. Podríamos escoger cualquier rectángulo (no superpuesto) cuyo fondo se encuentre dentro del intervalo en el eje x, y cuyas partes superiores se crucen con la curva en alguna parte. Pero es más fácil elegir rectángulos que (a) tengan todos el mismo ancho y (b) tomen sus alturas de la función en un borde. A continuación se muestran gráficas que muestran dos formas de usar cuatro rectángulos para aproximar esta área. En la primera gráfica, utilizamos puntos extremos izquierdos; la altura de cada rectángulo proviene del valor de la función en su borde izquierdo. En la segunda gráfica de la página siguiente, utilizamos puntos finales de la derecha.
Extremos izquierdos: El área es aproximadamente la suma de las áreas de los rectángulos. Cada rectángulo obtiene su altura de la función\( f(x)=\frac{1}{x} \) y cada rectángulo tiene un ancho de 1.
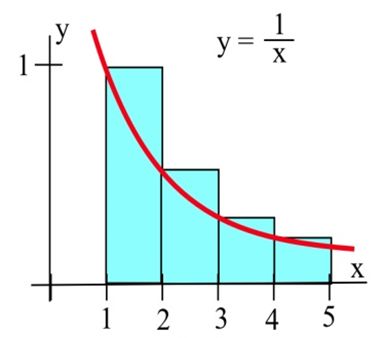
Puedes encontrar el área de cada rectángulo usando area = height\( \cdot \) width. Entonces el área total de los rectángulos, la estimación de la izquierda del área bajo la curva, es\[f(1)\cdot 1+f(2)\cdot 1+f(3)\cdot 1+f(4)\cdot 1=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}=\frac{25}{12}\approx 2.08.\nonumber \]
Observe que debido a que esta función está disminuyendo, todos los rectángulos de punto final izquierdo sobresalen por encima de la región que queremos; el uso de puntos finales izquierdos sobreestimará el área.
Puntos finales de la derecha: La estimación de la derecha del área es\[f(2)\cdot 1+f(3)\cdot 1+f(4)\cdot 1+f(5)\cdot 1=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\frac{77}{60}\approx 1.28.\nonumber \]
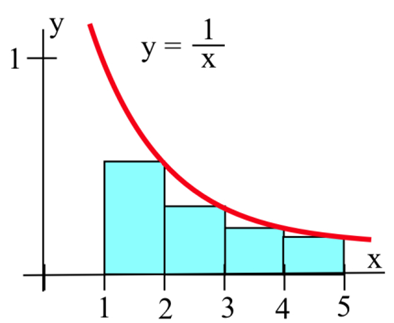
Todos los rectángulos de la derecha se encuentran completamente bajo la curva, por lo que esta estimación será una subestimación.
Podemos ver que el verdadero área está en realidad entre estas dos estimaciones. Entonces podríamos tomar su promedio:\[\text{Average}=\frac{\frac{25}{12}+\frac{77}{60}}{2}=\frac{101}{60}\approx 1.68\nonumber \]
En general, el promedio de las estimaciones de izquierda y derecha estará más cerca del área real que cualquiera de las estimaciones individuales.
Nuestra estimación del área bajo la curva es de aproximadamente 1.68. (El área real es de aproximadamente 1.61.)
Este applet te permitirá ver cómo cambia la aproximación si usas más rectángulos; cambia el control deslizante de posición
para alternar usando los extremos izquierdos, extremos derechos y puntos medios:
Si quisiéramos una mejor respuesta, podríamos usar rectángulos aún más y aún más estrechos. Pero hay un límite en cuanto a la cantidad de trabajo que queremos hacer a mano. En la práctica, elija un número manejable de rectángulos. Tendremos mejores métodos para obtener respuestas más precisas en poco tiempo.
Estas sumas de áreas de rectángulos se llaman sumas de Riemann. Es posible que veas una notación taquigráfica que se usa cuando la gente habla de sumas. No lo usaremos mucho en este libro, pero debes saber lo que significa.
Suma de Riemann
Una suma de Riemann para una función\(f(x)\) a lo largo de un intervalo\([a, b]\) es una suma de áreas de rectángulos que se aproximan al área bajo la curva. Comience dividiendo el intervalo\([a, b]\) en\(n\) subintervalos; cada subintervalo será la base de un rectángulo. Normalmente hacemos todos los rectángulos del mismo ancho\( \Delta x \). La altura de cada rectángulo proviene de la función evaluada en algún momento de su subintervalo. Entonces la suma de Riemann es\[f(x_1)\Delta x+f(x_2)\Delta x+f(x_3)\Delta x+\dots +f(x_n)\Delta x\nonumber \] o, factorizando la\( \Delta x \),\[\Delta x\left(f(x_1)+f(x_2)+f(x_3)+\dots +f(x_n)\right).\nonumber \]
Notación Sigma
La letra griega mayúscula Sigma\( \sum \) se utiliza para representar suma
. La notación sigma es una forma de representar de manera compacta una suma de muchos términos similares, como una suma de Riemann.
Usando la notación Sigma, se puede escribir la suma de Riemann\[\sum\limits_{i=1}^n f\left(x_i\right)\Delta x.\nonumber \]
Esto se lee en voz alta como la suma como\(i\) va de 1 a\(n\)\(f\) de\(x\) sub\(i\) veces Delta\(x\).
El \(i\)
es un contador o índice, como podrías haber visto en una clase de programación.
Definición de la Integral Definida
Debido a que el área bajo la curva es tan importante, tiene un vocabulario y notación especiales.
La integral definida de una función positiva\(f(x)\) a lo largo de un intervalo\([a, b]\) es el área entre\(f\), el\(x\) -eje,\(x = a\) y\(x = b\).
La integral definitiva de una función positiva\(f(x)\) de\(a\) a\(b\) es el área bajo la curva entre\(a\) y\(b\).
Si\(f(t)\) representa una tasa positiva (en\(y\) -unidades por\(t\) -unidades), entonces la integral definida de\(f(t)\) desde\(a\) a\(b\) es el total\(y\) -unidades que se acumulan entre\(t = a\) y\(t = b\).
Notación para la Integral Definitiva
La integral definitiva de\(f(x)\) de\(a\) a\(b\) está escrita\[\int_a^b f(x)\, dx.\nonumber \]
El\( \int \) símbolo se llama signo integral; es una letra alargada S, que representa suma
. (El\( \int \) corresponde a la\( \sum \) de la suma de Riemann)
¡El\(dx\) en el extremo debe estar incluido! El\(dx\) dice cuál es la variable — en este ejemplo, la variable es\(x\). (El\(dx\) corresponde a la\( \Delta x \) de la suma de Riemann)
La función\(f\) se llama integrando.
Los\(a\) y\(b\) se llaman los límites de la integración.
Formas verbales
Integramos, o encontramos la integral definitiva de una función. Este proceso se llama integración.
Definición Algebraica Formal
\[\int_a^b f(x)\, dx =\lim\limits_{n\to\infty}\sum\limits_{i=1}^n f(x_i)\Delta x.\nonumber \]
Definición práctica
La integral definida se puede aproximar con una suma de Riemann (dividiendo el área en rectángulos donde la altura de cada rectángulo proviene de la función, calculando el área de cada rectángulo y sumando). Cuantos más rectángulos usemos, cuanto más estrechos sean los rectángulos, mejor será nuestra aproximación.
Mirando hacia el futuro
Pronto tendremos métodos para computar valores exactos de algunas integrales definidas a partir de fórmulas. En muchos casos, incluso cuando se le da la función como tabla o gráfica, aún necesitará aproximar la integral definida con rectángulos.
El gráfico a continuación muestra\(y = r(t)\), el número de llamadas telefónicas realizadas por horas en un martes. Aproximadamente ¿cuántas llamadas se hicieron entre las 9 pm y las 11 pm? Expresar esto como una integral definitiva y aproximada con una suma Riemann.
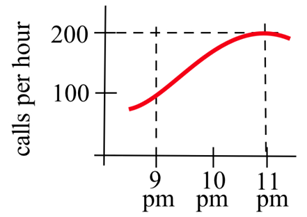
Solución
Sabemos que las llamadas acumuladas serán el área bajo esta gráfica de tarifas durante ese periodo de dos horas, la integral definitiva de esta tasa de\(t = 9\) a\(t = 11\).
El número total de llamadas será\( \int\limits_9^{11} r(t)\,dt \).
La parte superior aquí es una curva, así que no podemos obtener una respuesta exacta. Pero podemos aproximar el área usando rectángulos. Optemos por usar cuatro rectángulos y puntos finales izquierdos:
\[\int\limits_9^{11} r(t)\,dt \approx 0.5(100+150+180+195)=312.5\nonumber \]
Las unidades son llamadas por hora\( \cdot \) horas = llamadas. Nuestra estimación es que se realizaron alrededor de 312 llamadas entre las 9 pm y las 11 pm. ¿Es esto una subestimación o una sobreestimación?
Describir el área entre la gráfica de\(f(x) = \frac{1}{x}\), el\(x\) eje y las líneas verticales en\(x = 1\) y\(x = 5\) como una integral definida.
Solución
Esta es la misma área que estimamos que antes era de aproximadamente 1.68. Ahora podemos usar la notación de la integral definida para describirla. Nuestra estimación de\( \int\limits_1^5 \frac{1}{x}\, dx \) fue de 1.68. El verdadero valor de\( \int\limits_1^5 \frac{1}{x}\, dx \) es de aproximadamente 1.61.
Utilizando la idea de área, determinar el valor de\( \int\limits_1^3 1+x \,dx \).
Solución
\( \int\limits_1^3 1+x \,dx \)representa el área entre la gráfica de\(f(x) = 1+x\), el\(x\) eje -y las líneas verticales en 1 y 3.
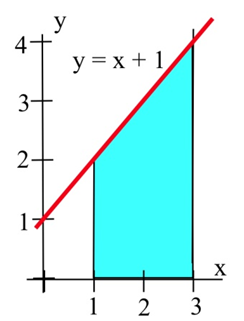
Dado que esta área se puede dividir en un rectángulo y un triángulo, podemos encontrar el área exactamente. El área es igual\[ 4 + \frac{1}{2}(2)(2) = 6 \text{ units}^2.\nonumber \]
En la tabla se muestran las tasas de crecimiento poblacional de Berrytown durante varios años. Utilice esta tabla para estimar el crecimiento poblacional total de 1970 a 2000:
| Año,\( t \) | 1970 | 1980 | 1990 | 2000 |
| Tasa de crecimiento poblacional\( R(t) \) en miles de personas por año | 1.5 | 1.9 | 2.2 | 2.4 |
Solución
La integral definitiva de esta tasa dará el cambio total de población a lo largo del periodo de treinta años. Solo tenemos unas pocas piezas de información, así que solo podemos estimar. A pesar de que no hemos hecho una gráfica, seguimos aproximando el área bajo la curva de velocidad, usando rectángulos. ¿Qué tan anchos son los rectángulos? Tenemos información cada 10 años, por lo que los rectángulos tienen un ancho de 10 años. ¿Cuántos rectángulos? Ten cuidado aquí —esto es un lapso de treinta años, entonces hay tres rectángulos.
- Uso de puntos finales de la izquierda: (1.5) (10) + (1.9) (10) + (2.2) (10) = 56
- Uso de puntos finales de la derecha: (1.9) (10) + (2.2) (10) + (2.4) (10) = 65
Tomando el promedio de estos dos:\[\frac{56+65}{2}=60.5\nonumber \]
Nuestra mejor estimación del crecimiento poblacional total de 1970 a 2000 es de 60.5 mil personas.
Área Firmada
Te habrás dado cuenta de que hasta este punto, hemos insistido en que el integrando (la función que estamos integrando) sea positivo. Eso es porque hemos estado hablando de área, lo que siempre es positivo.
Si la altura
(de la función) es un número negativo, entonces multiplicarlo por el ancho no nos da área real, nos da el área con signo negativo.
Pero resulta útil pensar en la posibilidad de área negativa. Ampliaremos nuestra idea de una integral definida ahora para incluir integros que tal vez no siempre sean positivos. Las alturas
de los rectángulos, los valores de la función, ahora podrían no ser siempre positivos.
La integral definida de una función\(f(x)\) a lo largo de un intervalo\([a, b]\) es el área firmada entre\(f\), el\(x\) -eje,\(x = a\) y\(x = b\).
La integral definida de una función\(f(x)\) de\(a\) a\(b\) es el área señalizada bajo la curva entre\(a\) y\(b\).
Si la función es positiva, el área firmada es positiva, como antes (y podemos llamarla área.)
Si la función cae por debajo del\(x\) eje, las áreas de las regiones por debajo del\(x\) eje vienen con un signo negativo. En este caso, no podemos llamarlo simplemente área.
Estas áreas negativas le quitan a la integral definida.
\( \int\limits_a^b f(x) \,dx = \)(Área por encima\( x \) del eje)\( - \) (Área por debajo\( x \) del eje)
Si\(f(t)\) representa una tasa positiva (en\(y\) -unidades por\(t\) -unidades), entonces la integral definida de\(f\) desde\(a\) a\(b\) es el total\(y\) -unidades que se acumulan entre\(t = a\) y\(t = b\).
Si\(f(t)\) representa cualquier tasa (en\(y\) -unidades por\(t\) -unidades), entonces la integral definida de\(f\) desde\(a\) a\(b\) es la neta\(y\) -unidades que se acumulan entre\(t = a\) y\(t = b\).
Encuentra la integral definida de\(f(x) = –2\) en el intervalo [1,4].
Solución
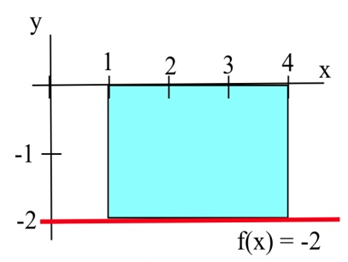
\(\int\limits_1^4 -2\,dx\)es el área firmada de la región que se muestra a la derecha. La región se encuentra por debajo del\( x \) eje, por lo que el área, 6, entra con un signo negativo. Entonces lo es la integral definitiva\(\int\limits_1^4 -2\,dx =-6\).
Las tasas negativas indican que la cantidad está disminuyendo. Por ejemplo, si\(f(t)\) es la velocidad de un automóvil en la dirección positiva a lo largo de una línea recta en el tiempo\(t\) (millas/hora), entonces los valores negativos de\(f\) indican que el automóvil está viajando en la dirección negativa, hacia atrás. La integral definitiva de\(f\) es el cambio de posición del automóvil durante el intervalo de tiempo. Si la velocidad es positiva, se acumula la distancia positiva. Si la velocidad es negativa, la distancia en la dirección negativa se acumula.
Esto es cierto de cualquier tipo. Por ejemplo, si\(f(t)\) es la tasa de cambio poblacional (personas/año) para un pueblo, entonces los valores negativos de\(f\) indicarían que la población de la localidad se estaba haciendo más pequeña, y la integral definitiva (ahora un número negativo) sería el cambio en la población, una disminución, durante el intervalo de tiempo.
En 1980 había 12 mil patos anidando alrededor de un lago, y la tasa de cambio poblacional (en patos por año) se muestra en la siguiente figura. Escribir una integral definitiva para representar el cambio total en la población de patos de 1980 a 1990, y estimar la población en 1990.
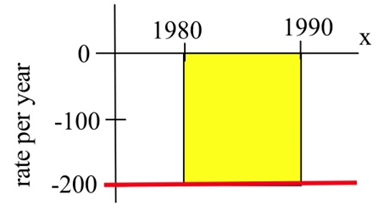
Solución
El cambio en la población es:\[ \begin{align*} \int\limits_{1980}^{1990} f(t) \,dt & = -(\text{area between \( f \) and axis}) \\ & \approx -(200\text{ ducks/year})\cdot (10\text{ years}) \\ & = -2000\text{ ducks} \end{align*} \nonumber \]
Entonces (1990 población de patos) = (población 1980) + (cambio de 1980 a 1990) = (12,000) + (-2000) = 10,000 patos.
Un error comienza en la ubicación\(x = 12\) del\(x\) eje -a la 1 pm camina a lo largo del eje con la velocidad que\(v(x)\) se muestra en la gráfica. ¿Hasta dónde viaja el error entre la 1 pm y las 3 pm, y dónde está el error a las 3 pm?
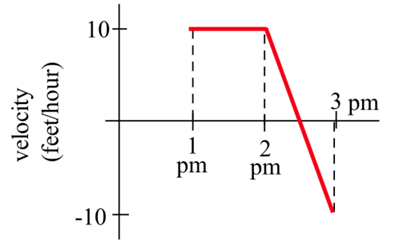
Solución
Tenga en cuenta que la velocidad es positiva desde 1 hasta las 2:30, luego se vuelve negativa. Entonces el bicho se mueve en la dirección positiva desde la 1 hasta las 2:30, luego se da la vuelta y retrocede hacia donde empezó. El área bajo la curva de velocidad de 1 a 2:30 muestra la distancia total recorrida por el insecto en la dirección positiva; el insecto se movió 12.5 pies en la dirección positiva. El área entre la curva de velocidad y el eje x, entre 2:30 y 3, muestra la distancia total recorrida por el insecto en dirección negativa, de regreso a casa; el insecto viajó 2.5 pies en dirección negativa. La integral definida de la curva de velocidad,\(\int\limits_1^3 v(t) \,dt\), muestra el cambio neto en la distancia:\[\int\limits_1^3 v(t) \,dt = 12.5-2.5=10.\nonumber \]
El bicho terminó 10 pies más lejos en la dirección positiva de lo que inició. A las 3 de la tarde, el error está a las\(x = 22\).
Utilice la gráfica a continuación para calcular\( \int\limits_0^2 f(x) \,dx \),\( \int\limits_2^4 f(x) \,dx \),\( \int\limits_4^5 f(x) \,dx \), y\( \int\limits_0^5 f(x) \,dx \).
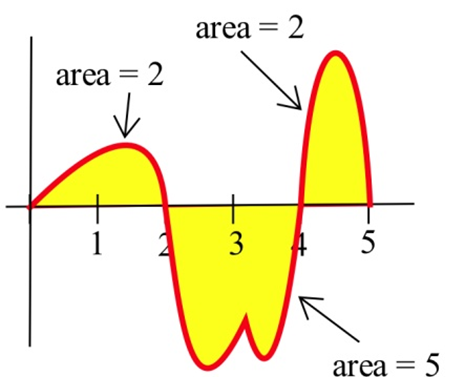
Solución
Usando las áreas dadas,\( \int\limits_0^2 f(x) \,dx = 2 \),\( \int\limits_2^4 f(x) \,dx = -5 \)\( \int\limits_4^5 f(x) \,dx = 2 \), y\( \int\limits_0^5 f(x) \,dx = \) (área arriba)\( - \) (área abajo)\( = (2+2) - (5) = -1\).
Aproximación con la tecnología
Si tu función se da como una gráfica o tabla, aún tendrás que aproximar integrales definidas usando áreas, generalmente de rectángulos. Pero si tu función se da como fórmula, puedes recurrir a la tecnología para obtener una mejor respuesta aproximada. Por ejemplo, la mayoría de las calculadoras gráficas tienen algún tipo de herramienta de integración numérica incorporada. También puedes encontrar muchas herramientas en línea que pueden hacer esto; escribe integración numérica en cualquier buscador para ver una selección de estas.
La mayoría de las herramientas de integración numérica utilizan rectángulos para estimar el área firmada, tal como lo harías a mano. Pero usan muchos más rectángulos de los que tendrías la paciencia para, así obtienen una mejor respuesta. Algunos de ellos utilizan sistemas informáticos de álgebra para encontrar respuestas exactas; aprenderemos a hacerlo nosotros mismos más adelante en este capítulo.
Cuando recurras a la tecnología para encontrar el valor de una integral definida, ten cuidado. No todas las herramientas podrán darte una respuesta correcta para cada integral. Primero debes hacer una estimación de la respuesta tú mismo para que puedas juzgar si la respuesta que obtienes tiene sentido.
Utilizar la tecnología para aproximar la integral definida\( \int\limits_1^5 \frac{1}{x} \,dx \). (Esta es la misma integral definida que aproximamos con rectángulos antes.)
Solución
Podríamos usar el siguiente comando en GeoGebra para aproximar esta integral:
Integral [1/x, 1, 5]
O haga clic en este enlace para ver cómo evaluar esta integral usando Wolfram|Alpha.
Utilizar la tecnología para aproximar la integral definida\( \int\limits_1^2 e^{x^2+x} \,dx \).
Solución
La función aquí es positiva, por lo que debe haber alguna área debajo de la curva aquí. No hay una manera algebraica de encontrar la respuesta exacta, por lo que algunos programas pueden simplemente devolver la integral original en lugar de intentar aproximarla.
Podríamos usar el siguiente comando en GeoGebra para aproximar esta integral:
Integral [e^ (x^2 + x), 1, 2]
O haz clic en este enlace para ver cómo aproximar esta integral usando Wolfram|Alpha. Aunque parece que Wolfram|Alpha puede evaluar la integral, la función Erfi
que muestra en su respuesta está realmente definida en términos de otra integral, por lo que aún no ha encontrado una respuesta algebraica.
Acumulación en la vida real
Ya hemos visto que el área
bajo una gráfica puede representar cantidades cuyas unidades no son las habituales unidades geométricas de metros cuadrados o pies cuadrados. Por ejemplo, si\(t\) es una medida de tiempo en segundos y\(f(t)\) es una velocidad con unidades pies/segundo, entonces la integral definida tiene unidades (pies/segundo)\( \cdot \) (segundos) = pies.
En general, las unidades para la integral definida\( \int\limits_a^b f(x)\,dx \) son (\(y\)-unidades)\( \cdot \) (\(x\)-unidades). Una comprobación rápida de las unidades puede ayudar a evitar errores en la configuración de un problema aplicado.
En ejemplos anteriores, observamos una función que representaba una tasa de desplazamiento (millas por hora); en ese caso, el área representaba la distancia total recorrida. Para funciones que representan otras tasas como la producción de una fábrica (bicicletas por día), o el flujo de agua en un río (galones por minuto) o el tráfico sobre un puente (automóviles por minuto), o la propagación de una enfermedad (personas recién enfermas por semana), el área seguirá representando el total cantidad de algo.
Supongamos que\(MR(q)\) es el ingreso marginal en dólares/artículo para la venta de\(q\) artículos. ¿Qué\( \int\limits_0^{150} MR(q) \,dq \) representa?
Solución
\( \int\limits_0^{150} MR(q) \,dq \)tiene unidades (dólares/artículo)\( \cdot \) (artículos) = dólares, y representa los dólares acumulados para vender de 0 a 150 artículos. Es decir\( \int\limits_0^{150} MR(q) \,dq = TR(150) \), los ingresos totales por vender 150 artículos.
Supongamos que\(r(t)\), en centímetros al año, representa cómo cambia el diámetro de un árbol con el tiempo. ¿Qué\( \int\limits_{T_1}^{T_2} r(t) \,dt \) representa?
Solución
\( \int\limits_{T_1}^{T_2} r(t) \,dt \)tiene unidades de (centímetros por año)\( \cdot \) (años) = centímetros, y representa el crecimiento acumulado del diámetro del árbol de\(T_1\) a\(T_2\). Es decir,\( \int\limits_{T_1}^{T_2} r(t) \,dt \) es el cambio en el diámetro del árbol a lo largo de este periodo de tiempo.


