3.3: El teorema fundamental y la antidiferenciación
- Page ID
- 110509
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El teorema fundamental del cálculo
Esta sección contiene el teorema más importante y más utilizado del cálculo, el Teorema Fundamental del Cálculo. Descubierto independientemente por Newton y Leibniz a finales del siglo 1600, establece la conexión entre derivados e integrales, proporciona una manera de calcular fácilmente muchas integrales, y fue un paso clave en el desarrollo de las matemáticas modernas para apoyar el auge de la ciencia y la tecnología. El cálculo es una de las estructuras intelectuales más significativas de la historia del pensamiento humano, y el Teorema Fundamental del Cálculo es un ladrillo muy importante en esa hermosa estructura.
Si\(F(x)\) es una función donde\(F'(x) = f(x)\), entonces
\[ \int\limits_a^b f(x) \,dx = F(b) - F(a) \nonumber \]
Esto en realidad no es nuevo para nosotros; llevamos algún tiempo usando esta relación; simplemente no la hemos escrito de esta manera. Esto dice lo que hemos dicho antes: la integral definitiva de una tasa de\(a\) a\(b\) es la neta\(y\) -unidades, el cambio en\(y\), que se acumulan entre\(t = a\) y\(t = b\). Aquí acabamos de dejar claro que esa tasa es un derivado.
Pensar en la relación de esta manera nos da la clave para encontrar respuestas exactas para algunas integrales definidas. Si el integrando es el derivado de algunos\(F\), entonces tal vez podríamos simplemente encontrar\(F\) y restar —eso sería más fácil que aproximar con rectángulos. Retroceder por el proceso de diferenciación nos ayudará a evaluar integrales definidas.
Encuentra\(f(x)\) si\(f '(x) = 2x\).
Solución
Oooh, conozco este. Es\( f(x)=x^2+3 \). Oh, espera, ¿estabas pensando en otra cosa? Sí, supongo que tienes razón, también\( f(x)=x^2 \) funciona. Así lo hace\( f(x)=x^2-\pi \), y\( f(x)=x^2+104,\!589.2 \). De hecho, hay muchas respuestas.
De hecho, hay infinitamente muchas funciones que todas tienen la misma derivada. Y eso tiene sentido — la derivada nos habla de la forma de la función, pero no habla de la ubicación. Podríamos desplazar la gráfica hacia arriba o hacia abajo y la forma no se vería afectada, por lo que la derivada sería la misma.
Esto lleva a una de las definiciones más difíciles: prestar mucha atención a los artículos (
el
versus a), porque son importantes.
Una antiderivada de una función\(f(x)\) is any function \(F(x)\) where \(F'(x) = f(x)\).
La antiderivada de una función\(f(x)\) es toda una familia de funciones, escritas\(F(x) + C\), donde\(F'(x) = f(x)\) y\(C\) representa cualquier constante.
El antiderivado también se llama la integral indefinida.
Notación para el Antiderivado
El antiderivado de\(f\) está escrito\[\int f(x) \,dx\nonumber \]
Esta notación se asemeja a la integral definida, porque el Teorema Fundamental del Cálculo dice que los antiderivados y las integrales definidas están íntimamente relacionados. Pero en esta notación, no hay límites de integración.
El\( \int \) símbolo todavía se llama signo integral;\(dx\) el al final aún debe incluirse; todavía se puede pensar en\( \int \) y\(dx\) como paréntesis izquierdo y derecho. La función todavía\(f\) se llama integrando.
Formas Verbales
Antidiferenciamos, integramos, o encontramos la integral indefinida de una función. Este proceso se llama antidiferenciación o integración.
No hay familias pequeñas en el mundo de los antiderivados: si\(f\) tiene un antiderivado\(F\), entonces\(f\) tiene un número infinito de antiderivados y cada uno de ellos tiene la forma\(F(x) + C\).
Encuentra un antiderivado de\(2x\).
Solución
Podemos elegir cualquier función que nos guste siempre y cuando sea su derivada\(2x\), así podemos escoger, digamos,\( F(x)=x^2-5.2 \).
Encuentra el antiderivado de\(2x\).
Solución
Ahora necesitamos escribir toda la familia de funciones cuyas derivadas son\(2x\). Podemos usar la\( \int \) notación:\[\int 2x\, dx = x^2+C.\nonumber \] (¡No olvides el \( +C \)
!)
Encuentra\( \int e^x\, dx \).
Solución
Este es probablemente uno que recuerdes:\( e^x \) es su propio derivado, por lo que también es su propio antiderivado. El signo integral nos dice que necesitamos incluir a toda la familia de funciones, por lo que necesitamos que \(+C\)
al final:\[ \int e^x\, dx = e^x+C. \nonumber \]
Antiderivados Gráfica o Numéricamente
Otra forma de pensar sobre el Teorema Fundamental del Cálculo es resolver la expresión para\(F(b)\):
\[ \int\limits_a^b F'(x) \,dx=F(b) - F(a) \nonumber \]La integral definida de una derivada de\(a\) a\(b\) da el cambio neto en la función original.
\[F(b) = F(a) + \int\limits_a^b F'(x) \,dx \nonumber \]La cantidad que terminamos es la cantidad con la que comenzamos más el cambio neto en la función.
Esto nos permite obtener valores para el antiderivado —siempre y cuando tengamos un punto de partida, y sepamos algo sobre la zona.
Supongamos que\(F(t)\) tiene la derivada que\(f(t)\) se muestra a continuación, y supongamos que sabemos\(F(0) = 5\). Encuentra valores para\(F(1),\ F(2),\ F(3),\) y\(F(4)\).
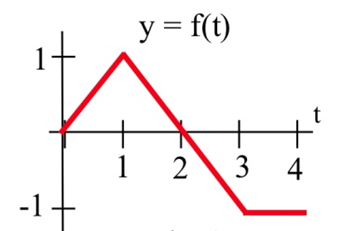
Solución
Usando la segunda forma de pensar sobre el Teorema Fundamental del Cálculo\( F(b) = F(a) + \int\limits_a^b F'(x) \,dx \),, podemos ver eso\( F(1) = F(0) + \int\limits_0^1 f(x) \,dx \). Conocemos el valor de\(F(0)\), y podemos encontrar fácilmente\( \int\limits_0^1 f(x) \,dx \) a partir de la gráfica, es solo el área de un triángulo. Entonces\[ \begin{align*} F(1) & = \\ & = 5+0.5 =5.5\\ F(2) & = F(0) + \int\limits_0^2 f(x) \,dx \\ & = 5+1=6 \end{align*} \nonumber \]
Tenga en cuenta que podemos partir de cualquier lugar del que conozcamos el valor; por ejemplo, ahora que sabemos\(F(2)\), podemos usar eso para encontrar\[ \begin{align*} F(3) & = F(2) + \int\limits_2^3 f(x) \,dx \\ & = 6-0.5=5.5 \\ F(4) & = F(3) + \int\limits_3^4 f(x) \,dx \\ & = 5.5-1=4.5 \end{align*} \nonumber \]
Aquí hay una copia del applet utilizado en este video:
\(F'(t) = f(t)\)se muestra a continuación. ¿Dónde\(F(t)\) tiene valores máximos y mínimos en el intervalo [0, 4]?
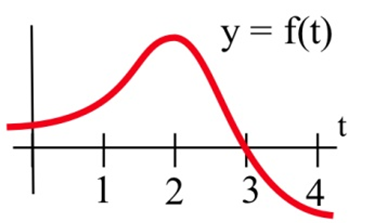
Solución
Ya que\( F(b) = F(a) + \int\limits_a^b F'(x) \,dx \), sabemos que\(F\) está aumentando siempre y cuando el área que se acumula debajo\(F' = f\) sea positiva (hasta\(t = 3\)), y luego disminuye cuando la curva se sumerge por debajo del\(x\) eje -para que el área negativa comience a acumularse. El área entre\(t = 3\) y\(t = 4\) es mucho menor que el área positiva que se acumula entre 0 y 3, por lo que sabemos que\(F(4)\) debe ser mayor que\(F(0)\). El valor máximo es cuándo\(t = 3\); el valor mínimo es cuándo\(t = 0\).
Tenga en cuenta que esta es una manera diferente de ver un problema que ya sabíamos resolver —en el Capítulo 2, habríamos encontrado puntos críticos de\(F\), dónde\(f = 0\): solo hay uno, cuándo\(t = 3\). \(f = F'\)va de positivo a negativo ahí, por lo que\(F\) tiene un máximo local en ese punto. Es el único punto crítico, por lo que debe ser un máximo global. Entonces miraríamos los valores de\(F\) en los puntos finales para encontrar cuál era el min global.
También podemos intentar esbozar una función basada en la gráfica de la derivada.
La gráfica a continuación muestra\(f'(x)\) — la tasa de cambio de\(f(x)\). Utilízala para bosquejar una gráfica de\(f(x)\) que satisfaga\(f(0) = 0\).
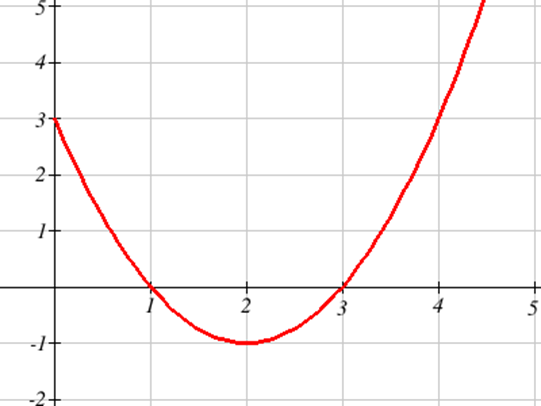
Solución
Recordemos del último capítulo las relaciones entre la gráfica de funciones y la gráfica derivada:
| \( f(x) \) | Incrementando | Disminuyendo | Cóncavo | Abajo cóncavo |
| \( f'(x) \) | \( + \) | \( - \) | Incrementando | Disminuyendo |
En la gráfica que se muestra, podemos ver que la derivada es positiva en el intervalo (0, 1) y\((3, \infty)\), por lo que la gráfica de\(f\) debería estar aumentando en esos intervalos. Asimismo,\(f\) debe estar disminuyendo en el intervalo (1,3).
En la gráfica,\(f'\) está disminuyendo en el intervalo (0, 2), por lo que\(f\) debe ser cóncavo hacia abajo en ese intervalo. Asimismo,\(f\) debe ser cóncavo hacia arriba en el intervalo\((2, \infty)\).
El derivado en sí no es suficiente información para saber dónde\(f\) comienza la función, ya que hay una familia de antiderivados, pero en este caso se nos da un punto específico en el que comenzar.
Para iniciar el boceto, podríamos anotar primero las formas que necesitamos:
luego dibuja las formas básicas:
Ahora podemos intentar bosquejar la gráfica, comenzando en el punto (0, 0). Observe que estamos dibujando esto de manera muy aproximada, ya que no tenemos mucha información con la que trabajar. Podemos decir, sin embargo, de la gráfica que el área de\(x = 0\) a\(x = 1\) es aproximadamente la misma que el área de\(x = 1\) a\(x = 3\), por lo que esperaríamos que el área neta de\(x = 0 \)\(x = 3\) a esté cerca de 0.
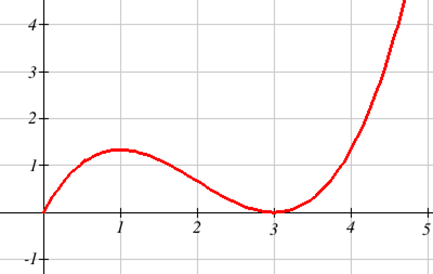
Resulta que esta gráfica no es horriblemente mala. Suavizarla daría una gráfica más cercana a la gráfica antiderivada real, que se muestra a continuación.
Derivada de la Integral
Existe otra conexión importante entre lo integral y lo derivado.
Si\[ A(x)=\int\limits_a^x f(t) \,dt \nonumber \] entonces\[ A'(x)=\frac{d}{dx}\int\limits_a^x f(t) \,dt =f(x). \nonumber \]
Es decir, la derivada de la función de acumulación es la función original.
Vamos\( F(x)=\int\limits_0^x f(t)\,dt \), donde\(f\) se grafica a continuación. Estimar\( F'(3) \).
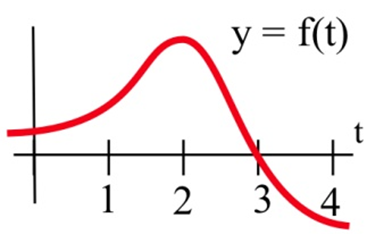
Solución
La función\(F(x)\) mide el área de\(t = 0\) a algunos\(t = x\). Para estimar\( F'(3) \), queremos estimar cuánto está aumentando el área cuando\(t = 3\). Dado que el valor de la función\(f(t)\) es 0 at\(t = 3\), el área no va a estar aumentando ni disminuyendo, por lo que podemos estimar\( F'(3) = 0 \).
Directamente usando el teorema fundamental del cálculo parte 2,\[ F'(x) = \frac{d}{dx}\int\limits_a^x f(t) \,dt = f(x) \nonumber \] así\[ F'(x) = f(3) = 0. \nonumber \]