3.9: Ecuaciones diferenciales

Una ecuación diferencial es una ecuación que involucra la derivada de una función. Nos permiten expresar con una simple ecuación la relación entre una cantidad y su tasa de cambio.

Ejemplo\(\PageIndex{1}\)

Un banco paga 2% de interés sobre sus cuentas de certificado de depósito, pero cobra una cuota anual de $20. Escribir una ecuación para la tasa de cambio del saldo,\( B'(t) \).

Solución

Si el saldo\( B(t) \) tiene unidades de dólares, entonces\( B'(t) \) tiene unidades de dólares por año. Cuando pensamos en lo que está cambiando el saldo de la cuenta, hay dos factores:

1. El interés, que aumenta el saldo, y
2. La cuota, que disminuye el saldo.

Considerando el interés, sabemos que cada año el saldo aumentará 2%, pero ¿2% de qué? Cada año eso va a cambiar, ya que ganamos intereses sobre cualquiera que sea el saldo actual. Podemos representar la cantidad de incremento como 2% del saldo:\( 0.02B(t) \) dólares/año.

El honorario ya cuenta con las unidades de dólares/año. Como ahora todo tiene las mismas unidades, podemos juntar las dos y crear la ecuación:\[ B'(t)=0.02B(t)-20. \nonumber \]

El resultado es un ejemplo de una ecuación diferencial. Observe que esta ecuación en particular involucra tanto la derivada como la función original, por lo que no podemos simplemente encontrar\( B(t) \) usando la integración básica.

Las ecuaciones algebraicas contienen constantes y variables, y las soluciones de una ecuación algebraica suelen ser números. Por ejemplo,\(x = 3\) y\(x = -2\) son soluciones de la ecuación algebraica\(x^2 = x + 6\). Las ecuaciones diferenciales contienen derivadas o diferenciales de funciones. Las soluciones de ecuaciones diferenciales son funciones. La ecuación diferencial\(y' = 3x^2\) tiene infinitamente muchas soluciones, y dos de esas soluciones son las funciones\(y = x^3 + 2\) y\(y = x^3 - 4\).

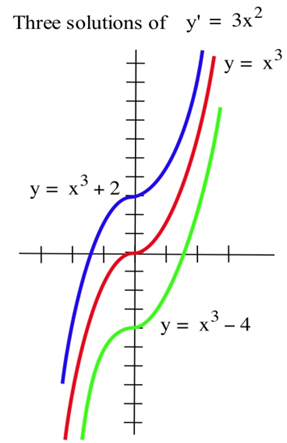
Ya has resuelto muchas ecuaciones diferenciales: cada vez que encuentras una antiderivada de una función\(f(x)\), resolviste la ecuación diferencial\(y' = f(x)\) para obtener una solución\(y\). La ecuación diferencial\(y' = f(x)\), sin embargo, es solo el comienzo. Otras aplicaciones generan diferentes ecuaciones diferenciales, como en el ejemplo de saldo bancario anterior.

Comprobación de Soluciones de Ecuaciones Diferenciales

Si una ecuación diferencial es fácil o difícil de resolver, es importante poder comprobar que una posible solución realmente satisface la ecuación diferencial.

Una posible solución de una ecuación algebraica se puede verificar poniendo la solución en la ecuación para ver si el resultado es verdadero:\(x = 3\) es una solución de\(5x + 1 = 16\) ya que\(5(3) + 1 = 16\) es verdadera. De igual manera, se puede verificar una solución de una ecuación diferencial sustituyendo la función y las derivadas apropiadas en la ecuación para ver si el resultado es verdadero:\(y = x^2\) es una solución de\(xy' = 2y\) since\(y' = 2x\) y\(x(2x) = 2\left(x^2\right)\) es true.

Ejemplo\(\PageIndex{2}\)

1. Compruebe que\(y = x^2 + 5\) es una solución de\(y'' + y = x^2 + 7\) y
2. Comprobar que\(y = x + \frac{5}{x}\) es una solución de\(y' + \frac{y}{x} = 2\).

Solución

1. \(y = x^2 + 5\)así\(y' = 2x\) y\(y'' = 2\). Sustituyendo estas funciones por\(y\) y\(y''\) en la ecuación diferencial\(y'' + y = x^2 + 7\), tenemos\[y'' + y = (2) + \left(x^2 + 5\right) = x^2 + 7,\nonumber \] así que\(y = x^2 + 5\) es una solución de la ecuación diferencial.
2. \(y = x + \frac{5}{x}\)así\(y' = 1 - \frac{5}{x^2}\). Sustituyendo estas funciones por\(y\) y\(y'\) en la ecuación diferencial\(y' + \frac{y}{x} = 2\), tenemos\[ y' + \frac{y}{x} = \left(1 - \frac{5}{x^2}\right) + \frac{1}{x}\left(x + \frac{5}{x}\right) = 1 - \frac{5}{x^2} + 1 + \frac{5}{x^2} = 2, \nonumber \] el resultado que queríamos verificar.

Ecuaciones diferenciales separables

Una ecuación diferencial se llama separable si las variables se pueden separar algebraicamente de manera que todos los\(x\)'s y\(dx\) son un lado de la ecuación, y todos los\(y\)'s y\(dy\) están en el otro lado de la ecuación. En otras palabras, entonces la ecuación tiene la forma\( f(x)\, dx=g(y)\, dy \).

Una vez separadas, las ecuaciones diferenciales separables se pueden resolver integrando ambos lados de la ecuación.

Ejemplo\(\PageIndex{3}\)

Encuentra la solución de\[ y'=\frac{6x+1}{2y}. \nonumber \]

Solución

Reescribir\(y'\) es un primer paso útil:\[ \frac{dy}{dx}=\frac{6x+1}{2y}\nonumber \]

Ahora podemos multiplicar ambos lados por\(dx\) y por\(2y\) para separar las variables:\[ 2y\, dy=(6x+1)\, dx \nonumber\]

Integrando cada lado, tenemos\[ \begin{align*} \int 2y\, dy & = \int (6x+1)\, dx \\ y^2+C_1 & = 3x^2+x+C_2 \end{align*} \nonumber \]

Observe que podemos combinar las dos constantes para crear una nueva constante consolidada\(C\), por lo que generalmente solo nos molestamos en poner una constante en el lado derecho:\[ y^2=3x^2+x+C. \nonumber \]

Como era de esperar, existe toda una familia de soluciones a esta ecuación diferencial.

Problema de Valor Inicial (IVT)

Un problema de valor inicial es una ecuación diferencial que proporciona información adicional sobre el valor inicial, o inicial, de la función. Esto nos permite luego resolver por la constante y encontrar una sola solución.

Ejemplo\(\PageIndex{4}\)

Encuentra la solución de la\( y'=\frac{6x+1}{2y} \) cual satisface\( y(2)=3 \).

Solución

En el ejemplo anterior encontramos la solución general,\( y^2=3x^2+x+C \).

Sustituyendo en la condición inicial,\(y = 3\) cuando\(x = 2\),\[3^2=3(2)^2+2+C,\nonumber \] así\( 9=12+2+C \), dando\( C=-5 \).

La solución es\[ y^2=3x^2+x-5. \nonumber \] A veces es deseable resolver para\(y\), lo que rendiría\( y=\pm\sqrt{3x^2+x-5} \), pero como la condición inicial tuvo un\(y\) valor positivo, aislamos la solución positiva:\[ y=\sqrt{3x^2+x-5}. \nonumber \]

Ejemplo\(\PageIndex{5}\)

Un banco paga 2% de interés sobre sus cuentas de certificado de depósito, pero cobra una cuota anual de $20. Si inicialmente inviertes $3,000, ¿cuánto tendrás después de 10 años?

Solución

Se puede reconocer esto como el ejemplo desde el inicio de la sección, para lo cual configuramos la ecuación\( B'(t)=0.02B(t)-20 \) o, más simplemente,\[ \frac{dB}{dt}=0.02B-20. \nonumber \]

Podemos separar esta ecuación multiplicando por\(dt\) y dividiendo por toda la expresión de la derecha:\[ \frac{dB}{0.02B-20}=dt. \nonumber \]

Integrar el lado izquierdo de esta ecuación requiere sustitución. Vamos\( u=0.02B-20 \), entonces\( du=0.02\, dB \). Haciendo la sustitución,\[ \begin{align*} \int\frac{dB}{0.02B-20} & = \int\frac{du/0.02}{u} \\ & = \int\frac{1}{u}\frac{du}{0.02} \\ & = \frac{1}{0.02}\int\frac{1}{u}\, du \\ & = \frac{1}{0.02}\ln|u|+C_1\\ & = \frac{1}{0.02}\ln|0.02B-20|+C_1 \end{align*} \nonumber \]

Integrar en el lado derecho de la ecuación diferencial es más fácil:\[\int dt = t+C_2\nonumber \]

Juntos, esto nos da la solución general a la ecuación diferencial (también estamos combinando los\( C \)'s en este paso):\[ \frac{1}{0.02}\ln|0.02B-20|=t+C \nonumber \]

Ahora nos gustaría resolver para\(B\). Comienza multiplicando por 0.02. \[ \begin{align*} \ln|0.02B-20| & = 0.02t+0.02C &\\ \ln|0.02B-20| & = 0.02t+D &\qquad\text{We can rename \( D=0.02C \) for simplicity.}\\ e^{\ln|0.02B-20|} & = e^{0.02t+D} &\qquad\text{Exponentiate both sides: \( e^{\text{left}}=e^{\text{right}} \).}\\ |0.02B-20| & = e^{0.02t+D} &\qquad\text{Use the log rule \( e^{\ln(A)}=A \).}\\ 0.02B-20 & = e^{0.02t+D} &\qquad\text{Since the RHS is always positive, we can drop the abs value.}\\ 0.02B-20 & = e^{0.02t}e^D &\qquad\text{Using the rule \( e^{A+B}=e^Ae^B \).}\\ 0.02B-20 & = ke^{0.02t} &\qquad\text{Rename \( k=e^D \).}\\ B & = \frac{ke^{0.02t}+20}{0.02}=\frac{ke^{0.02t}}{0.02}+1000 &\qquad\text{Add 20 and divide by 0.02.}\\ B & = Ae^{0.02t}+1000 &\qquad\text{Rename \( A=\frac{k}{0.02} \).} \end{align*} \nonumber \]

Finalmente, podemos sustituir nuestro valor inicial de\(B = 3000\) cuándo\(t = 0\) resolver por la constante\(A\):\[ \begin{align*} 3000 & = Ae^{0.02(0)}+1000 \\ A & = 2000 \end{align*} \nonumber \]

Esto nos da la ecuación para el saldo de la cuenta después de\(t\) años:\[ B(t)=2000e^{0.02t}+1000. \nonumber \]

Para encontrar el saldo después de 10 años, podemos evaluar esta ecuación en\(t = 10\):\[ B(10)=2000e^{0.02(10)}+1000\approx \$3442.81. \nonumber \]

Vale la pena señalar que esta respuesta no es exactamente correcta. Las ecuaciones diferenciales asumen cambios continuos, y es poco probable que los intereses se compongan continuamente o la tasa se extrae continuamente. Sin embargo, la respuesta probablemente esté cerca de la respuesta real, y las ecuaciones diferenciales proporcionan un modelo relativamente simple de una situación complicada.

Modelos de Crecimiento

El ejemplo de cuenta bancaria demostró un modelo básico de crecimiento: crecimiento proporcional a la cantidad existente. Las cuentas bancarias y las poblaciones tienden a crecer de esta manera si no se restringe. Este tipo de crecimiento se llama crecimiento ilimitado.

Crecimiento Ilimitado

Si una cantidad o población y crece a una tasa proporcional al tamaño de esa cantidad, se puede modelar con crecimiento ilimitado, que tiene la ecuación diferencial:\[ y'=ry, \nonumber \] donde\(r\) es una constante.

Ejemplo\(\PageIndex{6}\)

Una población crece 8% cada año. Si la población actual es de 5 mil, encuentre una ecuación para la población después de\(t\) años.

Solución

\[ \begin{align*} \frac{dy}{dt} & = 0.08y &\\ \frac{1}{y}\, dy & = 0.08\, dt &\qquad\text{Separate the variables.}\\ \ln|y| & = 0.08t+C &\qquad\text{Integrate both sides.}\\ e^{\ln|y|} & = e^{0.08t+C} &\qquad\text{Exponentiate both sides.}\\ y & = Ae^{0.08t} &\qquad\text{Simplify both sides, using the tricks we used in the bank example.} \end{align*} \nonumber \]

Ahora sustituya en la condición inicial:\( 5000=Ae^{0.08(0)} \), entonces\( A=5000 \).

La población crecerá siguiendo la ecuación\[ y=5000e^{0.08t}. \nonumber \]

Observe que la solución a la ecuación de crecimiento ilimitado es una ecuación exponencial.

Cuando un producto se anuncia fuertemente, las ventas tenderán a crecer muy rápidamente, pero eventualmente el mercado alcanzará la saturación, y las ventas se ralentizarán. En este tipo de crecimiento, denominado crecimiento limitado, la población crece a una tasa proporcional a la distancia desde el valor máximo.

Crecimiento Limitado

Si una cantidad crece a una tasa proporcional a la distancia desde el valor máximo,\(M\), it can be modeled with limited growth, which has the differential equation \[ y'=k(M-y), \nonumber \] where \(k\) is a constant, and \(M\) is the maximum size of \(y\).

Ejemplo\(\PageIndex{7}\)

Se introduce un nuevo celular. La compañía estima que venderán 200 mil teléfonos. Después de 1 mes han vendido 20 mil. ¿Cuántos habrán vendido después de 9 meses?

Solución

En este caso hay una cantidad máxima de teléfonos que esperan vender, así que\(M = 200\) mil. Modelando las ventas\(y\),, en miles de teléfonos, podemos escribir la ecuación diferencial\[ y'=k(200-y). \nonumber \]

Ya que era un teléfono nuevo,\( y(0)=0 \). También conocemos las ventas después de un mes,\( y(1)=20 \).

Resolviendo la ecuación diferencial:\[ \begin{align*} \frac{dy}{dt} & = k(200-y) &\\ \frac{dy}{200-y} & = k\, dt &\qquad\text{Separate the variables.}\\ -\ln|200-y| & = kt+C &\qquad\text{Integrate both sides. On the left use the substitution.}\\ e^{\ln|200-y|} & = e^{-kt+C} &\qquad\text{Multiply both sides by -1, and exponentiate both sides.}\\ 200-y & = Be^{-kt} &\qquad\text{Simplify.}\\ y & = Ae^{-kt}+200 &\qquad\text{Subtract 200, divide by -1, and simplify.} \end{align*} \nonumber \]

Usando la condición inicial\( y(0)=0 \),\[ 0=Ae^{-k(0)}+200, \nonumber \] así\( 0=A+200 \), dando\( A=-200 \).

Usando el valor\( y(1)=20 \):\[ \begin{align*} 20 & = -200e^{-k(t)}+200 &\\ \frac{=180}{-200} & = 0.9=e^{-k} &\qquad\text{Subtract 200 and divide -200.}\\ \ln(0.9) & = \ln\left(e^{-k}\right)=-k &\qquad\text{Take the ln of both sides.}\\ k & = -\ln(0.9)\approx 0.105 &\qquad\text{Divide by -1.} \end{align*} \nonumber \]

Como un rápido chequeo de cordura, este valor es positivo como cabría esperar, lo que indica que las ventas van creciendo con el tiempo. Ahora tenemos la ecuación para las ventas de teléfonos a lo largo del tiempo:\[ A=-200e^{-0.105t}+200. \nonumber \]

Finalmente, podemos evaluar esto en\(t = 9\) para encontrar las ventas después de 9 meses:\[ A(9)=-200e^{-0.105(9)}+200\approx 122.26\text{ thousand phones}. \nonumber \]

El crecimiento limitado también se usa comúnmente para los modelos de aprendizaje, ya que al aprender una nueva habilidad, las personas suelen aprender rápidamente al principio, luego su tasa de mejora se ralentiza a medida que se acercan al dominio.

Ejemplo\(\PageIndex{8}\)

Jim está aprendiendo un nuevo conjunto de códigos de producto para el trabajo. Cada día estudia, y pone a prueba su recuerdo. Supongamos que después de 4 días, Jim ha dominado el 70% de los nuevos códigos. ¿Cuánto tiempo le llevará dominar el 95% de los códigos, si se aplica el modelo de crecimiento limitado?

Solución

En este caso hay una cantidad máxima de dominio posible, por lo que\(M\) = 100%. Modelando su aprendizaje\(L\),, como porcentaje de maestría, podemos escribir la ecuación diferencial\(L'=k(100-L)\)

Resolviendo como hicimos en el ejemplo anterior, obtenemos\(L=Ae^{-kt}+100\).

Desde que empezó a no conocer ninguno de los códigos\(L(0)=0\), entonces\(0 = Ae^{-k(0)}+100\), así\(A = -100\).

Usando que Jim dominó 70 de los códigos en 4 días,\(L(4)=70\), entonces

\[\begin{align*} 70 = -100e^{-k(4)}+100 \\ -30 = -100e^{-k(4)} \\ 0.3 = e^{-k(4)} \\ \ln(0.3) = \ln \left(e^{-k(4)}\right) = -4k \\ k = \frac{\ln(0.3)}{-4} \approx 0.301 \end{align*}\]

Ahora tenemos la ecuación\(L = -100e^{-0.301t} + 100\), podemos resolver para cuándo\(L = 95\).

\[\begin{align*} 95 = -100e^{-0.301t}+100 \\ -5 = -100e^{-0.301t} \\ 0.05 = e^{-0.301t} \\ \ln(0.3) = \ln \left(e^{-0.301t}\right) = -0.301t \\ t = \frac{\ln(0.05)}{-0.301} \approx 9.95 \end{align*}\]

Jim habrá alcanzado el 95% de maestría después de unos 10 días.

Anteriormente utilizamos un crecimiento ilimitado para modelar una población, pero a menudo una población se verá limitada por la comida, el espacio y otros recursos. Cuando una población crece tanto proporcional a su tamaño, como relativo a la distancia desde algún máximo, eso se denomina crecimiento logístico. Esto lleva a la ecuación diferencial\( y'=ky(M-y) \), que es precisa pero no siempre conveniente de usar. Usaremos una ligera modificación. Dado que resolver esta ecuación diferencial requiere técnicas de integración que no hemos aprendido, se da la forma de solución.

Crecimiento Logístico

Si una cantidad crece a una tasa proporcional a su tamaño y a la distancia del valor máximo, crecimiento\(M\), it can be modeled with logístico, que tiene la ecuación diferencial:\[ y'=ry\left(1-\frac{y}{M}\right). \nonumber \]

\(r\)puede interpretarse como la tasa de crecimiento sin restricciones, es decir, cómo crecería la población si no hubiera un valor máximo.

Esta ecuación diferencial tiene soluciones de la forma\[ y=\frac{M}{1+Ae^{-rt}}. \nonumber \]

Ejemplo\(\PageIndex{9}\)

Se introduce una colonia de 100 conejos en un bosque recuperado. Después de 1 año, la población ha crecido a 300. Se estima que el bosque puede sostener 5000 conejos. El servicio forestal planea reintroducir lobos al bosque cuando la población de conejos alcance los 3000 conejos. ¿Cuándo ocurrirá eso?

Solución

La población máxima sustentable se dio como\(M = 5000\). Usando el formulario de solución\[ y=\frac{M}{1+Ae^{-rt}} \nonumber \] y la condición inicial\( y(0)=100 \) podemos resolver para\( A \):\[ \begin{align*} 100 & = \frac{5000}{1+Ae^{-r(0)}} &\\ 100 & = \frac{5000}{1+A} &\qquad\text{Simplify.}\\ 100(1+A) & = 5000 &\qquad\text{Multiply both sides by \( 1+A \).}\\ 1+A & = 50 &\qquad\text{Divide by 100.}\\ A & = 49 & \end{align*} \nonumber \]

Ahora, usando\( y(1)=300 \), podemos resolver para\(r\):\[ \begin{align*} 300 & = \frac{5000}{1+49e^{-r(1)}} \\ 300\left(1+49e^{-r}\right) & = 5000 \\ 1+49e^{-r} & = \frac{5000}{300} \\ e^{-r} & = \frac{\frac{50}{3}-1}{49}\approx 0.3197 \\ -r & = \ln(0.3197) \\ r & = -\ln(0.3197)\approx 1.1404 \end{align*} \nonumber \]

Ahora tenemos la ecuación para la población después de\(t\) años:\[ y=\frac{5000}{1+49e^{-1.1404t}}. \nonumber \]

Para responder a la ecuación original, de cuándo la población de conejos llegará a 3000, necesitamos resolver para\(t\) cuándo\(y = 3000\):\[ \begin{align*} 3000 & = \frac{5000}{1+49e^{-1.1404t}} \\ 3000\left(1+49e^{-1.1404t}\right) & = 5000 \\ e^{-1.1404t} & = \frac{\frac{5}{3}-1}{49}\approx 0.01361 \\ t & = \frac{\ln(0.01361)}{-1.1404}\approx 3.77\text{ years}. \end{align*} \nonumber \]

El crecimiento logístico también es un buen modelo para ventas no anunciadas. Un nuevo producto que no se anuncie hará que las ventas aumenten lentamente al principio, luego crecerán a medida que se propague el boca a boca y la gente se familiarice con el producto. Las ventas se nivelarán cuando se acerquen a la saturación del mercado.