3.E: La Integral (Ejercicios)
- Page ID
- 110522
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3.1 Ejercicios
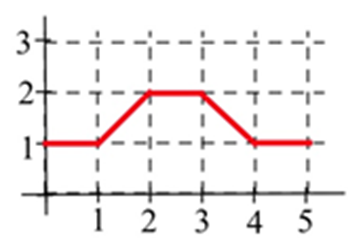
Dejar\(A(x)\) representar el área delimitada por la gráfica y el eje horizontal y las líneas verticales en\(t=0\) y\(t=x\) para la gráfica mostrada. Evaluar\(A(x)\) para\(x =\) 1, 2, 3, 4 y 5.
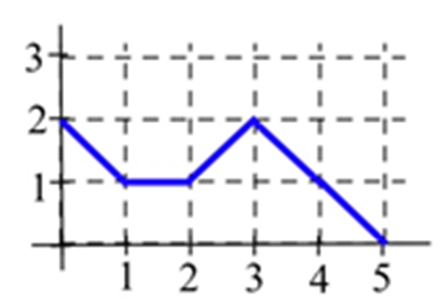
Dejar\(B(x)\) representar el área delimitada por la gráfica y el eje horizontal y las líneas verticales en\(t=0\) y\(t=x\) para la gráfica mostrada. Evaluar\(B(x)\) para\(x =\) 1, 2, 3, 4 y 5.
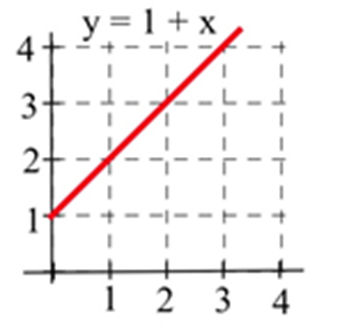
Dejar\(C(x)\) representar el área delimitada por la gráfica y el eje horizontal y las líneas verticales en\(t=0\) y\(t=x\) para la gráfica mostrada. Evalúe\(C(x)\) para\(x =\) 1, 2 y 3 y encuentre una fórmula para\(C(x)\).
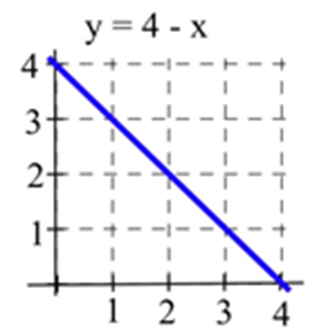
Dejar\(A(x)\) representar el área delimitada por la gráfica y el eje horizontal y las líneas verticales en\(t=0\) y\(t=x\) para la gráfica mostrada. Evalúe\(A(x)\) para\(x =\) 1, 2 y 3 y encuentre una fórmula para\(A(x)\).
Un automóvil tenía la velocidad que se muestra en la gráfica de la derecha.
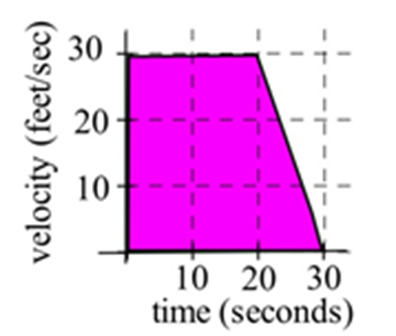
Un automóvil tenía la velocidad que se muestra en la gráfica de la derecha. ¿A qué distancia viajó el auto\(t= 0\) a\(t = 30\) segundos?
Un auto tenía la velocidad que se muestra a continuación.
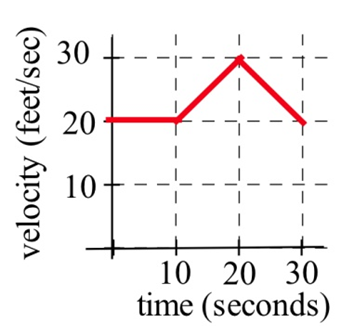
¿A qué distancia viajó el auto de\(t = 0\) a\(t = 30\) segundos?
Las velocidades de dos autos se muestran en la gráfica.
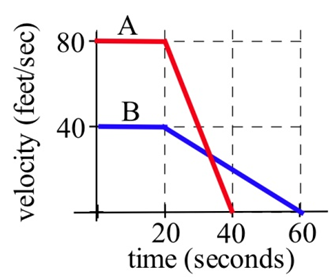
(a) A partir del momento en que se aplicaron los frenos, ¿cuántos segundos tardó cada auto en detenerse?
b) A partir del momento en que se aplicaron los frenos, ¿qué carro viajó más lejos hasta llegar a una parada completa?
Tú y un amigo parten al mediodía y caminan en la misma dirección por el mismo camino a las tarifas que se muestran.
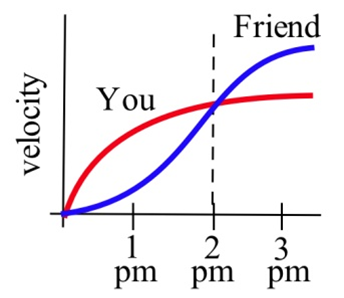
a) ¿Quién camina más rápido a las 2 de la tarde? ¿Quién se adelanta a las 2 pm?
b) ¿Quién camina más rápido a las 3 de la tarde? ¿Quién está adelante a las 3 de la tarde?
(c) ¿Cuándo estarán juntos tú y tu amigo? (Responde con palabras.)
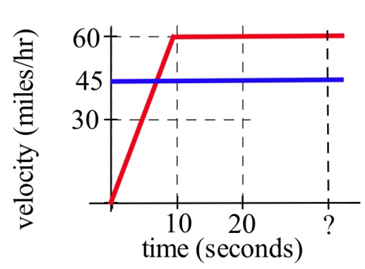
Persecución policial: Un velocista que viaja 45 millas por hora (en una zona de 25 mph) pasa por un carro policial detenido que inmediatamente despega después del velocista. Si el carro de policía acelera de manera constante a 60 millas/hora en 20 segundos y luego viaja a una constante 60 millas/hora, ¿cuánto tiempo y hasta qué punto antes de que el carro policial atrapa al velocista que siguió viajando a 45 millas/hora?
El agua fluye hacia una tina. En la tabla se muestra la velocidad a la que fluye el agua, en galones por minuto. La tina está inicialmente vacía.
|
\(t\), en minutos |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Caudal, en gal/min |
0.5 |
1.0 |
1.2 |
1.4 |
1.7 |
2.0 |
2.3 |
1.8 |
0.7 |
0.5 |
0.2 |
Use la tabla para estimar cuánta agua hay en la tina después
a. cinco minutos
b. diez minutos
En la tabla se muestran las lecturas del velocímetro para un viaje corto en automóvil.
|
\(t\), en minutos |
0 |
5 |
10 |
15 |
20 |
|
Velocidad, en mph |
0 |
30 |
40 |
65 |
40 |
a. Utilice la tabla para estimar hasta dónde viajó el automóvil a lo largo de los veinte minutos mostrados.
b. ¿Qué tan precisa esperaría que fuera su estimación?
La tabla muestra los valores de\(f(t)\). Usa la tabla para estimar\(\int^{40}_0 f(t) dt\).
|
\(t\) |
0 |
10 |
20 |
30 |
40 |
|
\(f(t)\) |
17 |
22 |
18 |
11 |
35 |
La tabla muestra los valores de\(g(x)\).
|
\(x\) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
\(g(x)\) |
140 |
142 |
144 |
152 |
154 |
165 |
200 |
Usa la tabla para estimar
| a.\(\int^3_0 g(x) dx\) | b\(\int^6_3 g(x) dx\) | c.\(\int^6_0 g(x) dx\) |
¿Cuáles son las unidades para el “área” de un rectángulo con las unidades de base y altura dadas?
| Unidades base | Unidades de altura | Unidades de “Área” |
|
millas por segundo |
segundos |
|
|
horas |
dólares por hora |
|
|
pies cuadrados |
pies |
|
|
kilovatios |
horas |
|
|
casas |
personas por casa |
|
|
comidas |
comidas |
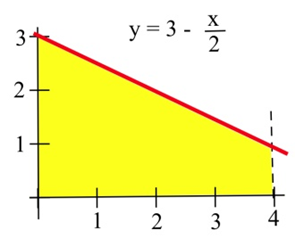
En los problemas 15 — 17, representar el área de cada región delimitada como una integral definida, y utilizar la geometría para determinar el valor de la integral definida.
15. La región delimitada por\(y = 2x \), el\(x\) eje —, la línea\(x = 1\), y\(x = 3\).
16. La región delimitada por\(y = 4 – 2x \), el\(x\) eje —y el\(y\) eje —.
17. La región sombreada en la gráfica a la derecha.
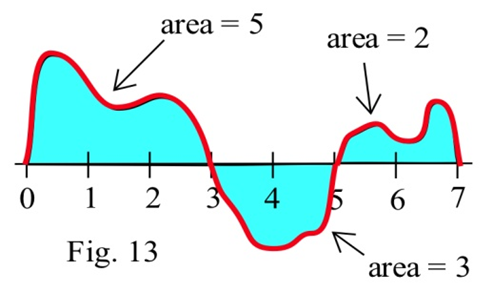
Usando la gráfica de áreas\(f\) mostradas y dadas de varias regiones, evalúe:
(a)\(\int^3_0 f(x) dx\)
b)\(\int^5_3 f(x) dx\)
c)\(\int^7_5 f(x) dx\)
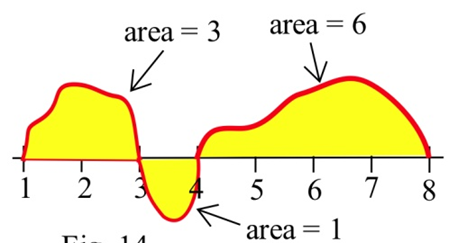
Usando la gráfica de áreas\(f\) mostradas y dadas de varias regiones, evalúe:
(a)\(\int^3_1 g(x) dx\)
b)\(\int^4_3 g(x) dx\)
c)\(\int^8_4 g(x) dx\)
d)\(\int^8_1 g(x) dx\)
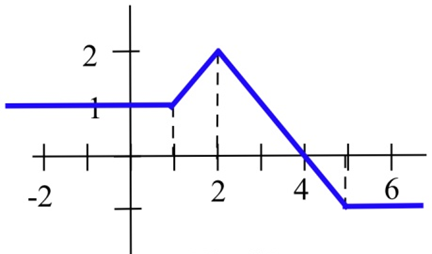
Utilice la gráfica para evaluar:
(a)\(\int^1_{-2} h(x) dx\)
b)\(\int^6_4 h(x) dx\)
c)\(\int^6_{-2} h(x) dx\)
d)\(\int^4_{-2} h(x) dx\)
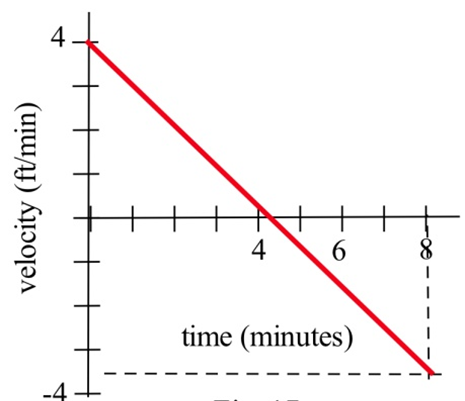
Su velocidad a lo largo de una carretera recta se muestra a la derecha. ¿Qué tan lejos viajaste en 8 minutos?
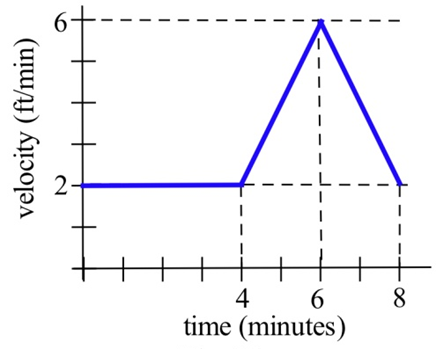
Su velocidad a lo largo de una carretera recta se muestra a continuación. ¿Cuántos pies caminaste en 8 minutos?
En los problemas 23 - 26, las unidades se dan para\(x\) y para\(f(x)\). Dar las unidades de\(\int^b_a f(x) dx\).
23. \(x\)es tiempo en “segundos”, y\(f(x)\) es velocidad en “metros por segundo”.
24. \(x\)es tiempo en “horas”, y\(f(x)\) es un caudal en “galones por hora”.
25. \(x\)es una posición en “pies”, y\(f(x)\) es un área en “pies cuadrados”.
26. \(x\)es una posición en “pulgadas”, y\(f(x)\) es una densidad en “libras por pulgada”.
En los problemas 27 — 31, representan el área con una integral definida y utilizan la tecnología para encontrar la respuesta aproximada.
27. La región delimitada por\(y = x^3\), el\(x\) eje —, la línea\(x = 1\), y\(x = 5\).
28. La región delimitada por\(y = \sqrt{x}\), el\(x\) eje —y la línea\(x = 9\).
29. La región sombreada que se muestra a la derecha.
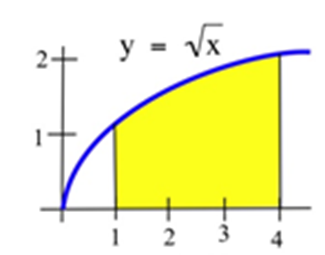
30. La región sombreada a continuación.
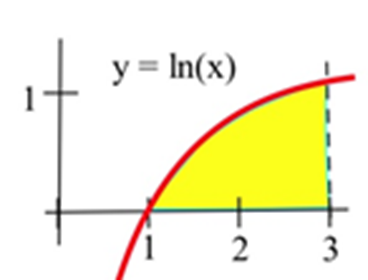
31. Considera la integral definitiva\(\int^3_0 (3+x) dx\).
(a) Utilizando seis rectángulos, encuentra la suma de Riemann de la izquierda para esta integral definida.
(b) Utilizando seis rectángulos, encontrar la suma de Riemann de la derecha para esta integral definida.
(c) Utilizando geometría, encontrar el valor exacto de esta integral definida.
Considera la integral definitiva\(\int^2_0 x^3 dx\).
(a) Usando cuatro rectángulos, encuentra la suma de Riemann de la izquierda para esta integral definida.
(b) Utilizando cuatro rectángulos, encontrar la suma de Riemann de la derecha para esta integral definida.
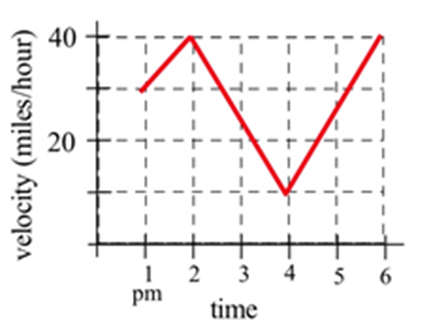
Escriba la distancia total recorrida por el automóvil en la gráfica entre la 1 pm y las 4 pm como integral definida y estime el valor de la integral.
Los problemas 34 — 41 se refieren a la gráfica de que\(f\) se muestra.
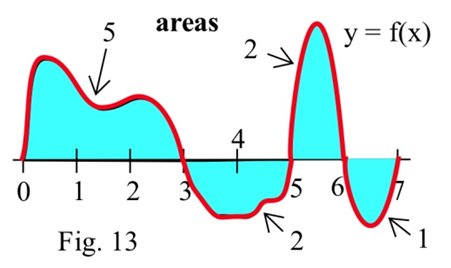
Utilice la gráfica para determinar los valores de las integrales definidas. (Los números en negrita representan el área de cada región).
| 34. \(\int^3_0 f(x) dx\) | 35. \(\int^5_3 f(x) dx\) | 36. \(\int^2_2 f(x) dx\) | 37. \(\int^7_6 f(w) dw\) |
| 38. \(\int^5_0 f(x) dx\) | 39. \(\int^7_0 f(x) dx\) | 40. \(\int^6_3 f(t) dt\) | 41. \(\int^7_5 f(x) dx\) |
Los problemas 42 — 47 se refieren a la gráfica de que\(g\) se muestra.
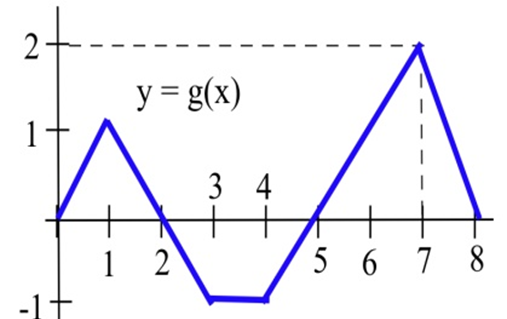
Utilice la gráfica para evaluar las integrales.
| 42. \(\int^2_0 g(x) dx\) | 43. \(\int^3_1 g(t) dt\) | 44. \(\int^5_0 g(x) dx\) |
| 45. \(\int^8_0 g(s) ds\) | 46. \(\int^3_0 2g(t) dt\) | 47. \(\int^8_5 1+g(x) dx\) |
3.2 Ejercicios
En los problemas 1 — 5, verificar que\(F(x)\) es un antiderivado del integrando\(f(x)\) y utilizar la Parte 2 del Teorema Fundamental para evaluar las integrales definidas.
| 1. \(\int^1_0 2x dx, F(x) = x^2 + 5\) | 2. \(\int^4_1 3x^2 dx, F(x) = x^3 + 2\) | 3. \(\int^3_1 x^2 dx, F(x) = \frac{1}{3} x^3\) |
| 4. \(\int^3_0 (x^2+4x - 3) dx , F(x) = \frac{1}{3} x^3 + 2x^2 – 3x\) | 5. \(\int^5_1 \frac{1}{x} dx, F(x) = \ln ( x )\) |
Dado\(A(x) = \int^x_0 2t dt\), encontrar\(A'(x)\)
Dado\(A(x) = \int^x_0 (3-t^2) dt\), encontrar\(A'(x)\)
Vamos\(A(x) = \int^x_0 f(t) dt\) para la función graficada aquí.
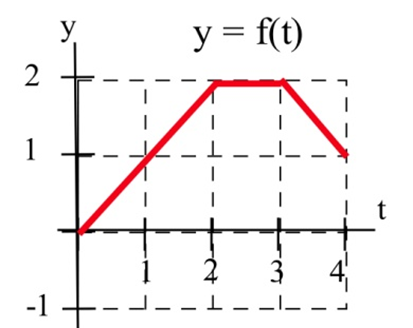
Evaluar\(A'(1)\),\(A'(2)\),\(A'(3)\).
Para los problemas 9-10, la gráfica proporcionada muestra\(g'(x)\). Úsalo bosquejar una gráfica de\(g(x)\) que satisfaga\(g(0) = 0\).
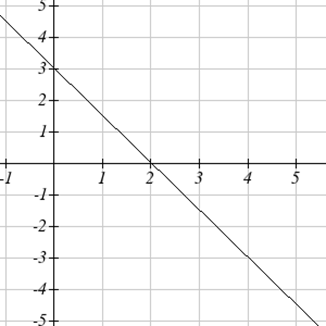
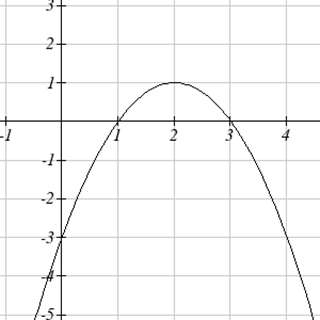
10.
3.3 Ejercicios
Para los problemas 1-10, encuentra el antiderivado indicado.
| 1. \(\int (x^3 - 14x + 5) dx\) | 2. \(\int (2.5x^5-x-1.25) dx\) |
| 3. \(\int 12.3 dy\) | 4. \(\int \pi^2 dw\) |
| 5. \(\int e^P dP\) | 6. \(\int \left( \sqrt{x} + e^x - \frac{1}{4x^3} \right) dx\) |
| 7. \(\int \frac{1}{x} dx\) | 8. \(\int \frac{1}{x^2} dx\) |
| 9. \(\int (x-2)(x+2) dx\) | 10. \(\int \frac{t^5-t^2}{t} dt\) |
Para los problemas 11-18, encontrar una antiderivada del integrando y utilizar el Teorema Fundamental para evaluar la integral definida.
| 11. \(\int^5_2 3x^2 dx\) | 12. \(\int^2_{-1} x^2 dx\) | 13. \(\int^3_1 (x^2+4x-3) dx\) | 14. \(\int^e_1 \frac{1}{x} dx\) |
| 15. \(\int^{100}_{25} \sqrt{x} dx\) | 16. \(\int^5_3 \sqrt{x} dx\) | 17. \(\int^{10}_1 \frac{1}{x^2} dx\) | 18. \(\int^{1000}_1 \frac{1}{x^2} dx\) |
Para los problemas 19 - 21 encuentra el área que se muestra en la figura.
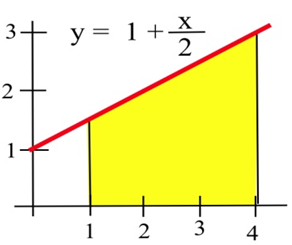
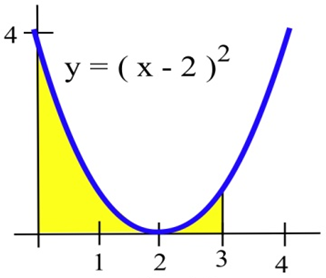
20.
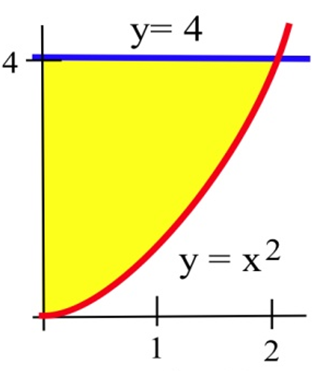
3.4 Ejercicios
Para los problemas 1-8, encuentra el antiderivado indicado.
| 1. \(\int \frac{1}{(4x+1)^3} dx\) | 2. \(\int e^{100x} dx\) |
| 3. \(\int (1.0003)^{12t} dt\) | 4. \(\int \frac{e^{10/x}}{x^2} dx\) |
| 5. \(\int \sqrt{w+5} dw\) | 6. \(\int 6x^2 \sqrt{3x^3-1} dx\) |
| 7. \(\int \frac{dx}{x\ln x}\) | 8. \(\int \frac{x-3}{x^2-6x+5} dx\) |
Para los problemas 9-12, encontrar un antiderivado del integrando y utilizar el Teorema Fundamental para evaluar la integral definida.
| 9. \(\int^2_{-2} \frac{2x}{1+x^2} dx\) | 10. \(\int^1_0 e^{2x} dx\) | 11. \(\int^{4}_2 (x-2)^3 dx\) | 12. \(\int^1_0 x \sqrt{1-x^2} dx\) |
3.5 Ejercicios
En los problemas 1—4,\(dv\) se da una función\(u\) o. Encuentra la pieza\(u\) o la\(dv\) que no se da, calcula\(du\) y\(v\), y aplica la Fórmula de Integración por Partes.
| 1. \(\int 12x \cdot \ln(x) dx\) | \(u = \ln(x)\) | 2. \(\int x \cdot e^{–x} dx\) | \(u = x\) |
| 3. \(\int x^4 \ln(x) dx\) | \(dv = x^4 dx\) | 4. \(\int x \cdot (5x + 1)^{19} dx\) | \(u = x\) |
En los problemas 5 - 10 evaluar las integrales
| 5. \(\int^1_0 \frac{x}{e^{3x}} dx\) | 6. \(\int^1_0 10x \cdot e^{3x} dx\) | 7. \(\int^3_1 \ln (2x + 5) dx\) |
| 8. \(\int x^3 \ln (5x) dx\) | 9. \(\int x \ln (x + 1) dx\) | 10. \(\int^2_1 \frac{\ln (x)}{x^2} dx\) |
Para problemas 11 - 14 integrar cada función.
| 11. \(\int \frac{1}{4-x^2}\) | 12. \(\int \frac{2}{9-x^2}\) | 13. \(\int \sqrt{4+x^2}\) | 14. \(\int \sqrt{9+x^2}\) |
3.6 Ejercicios
En los problemas 1 — 4, utilice los valores de la tabla para estimar las áreas.
| \(x\) | \(f(x)\) | \(g(x)\) | \(h(x)\) |
|
0 |
5 |
2 |
5 |
|
1 |
6 |
1 |
6 |
|
2 |
6 |
2 |
8 |
|
3 |
4 |
2 |
6 |
|
4 |
3 |
3 |
5 |
|
5 |
2 |
4 |
4 |
|
6 |
2 |
0 |
2 |
1. Estimar el área entre\(f\) y\(g\), entre\(x = 0\) y\(x = 4\).
2. Estimar el área entre\(g\) y\(h\), entre\(x = 0\) y\(x = 6\).
3. Estimar el área entre\(f\) y\(h\), entre\(x = 0\) y\(x = 4\).
4. Estimar el área entre\(f\) y\(g\), entre\(x = 0\) y\(x = 6\).
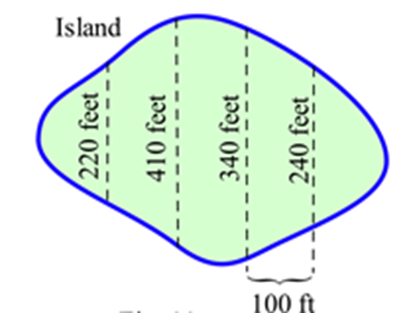
Estimar el área de la isla mostrada
En los problemas 6 — 15, encuentra el área entre las gráficas de\(f\) y\(g\) para\(x\) en el intervalo dado. ¡Recuerda dibujar la gráfica!
| 6. \(f(x) = x^2 + 3 \),\(g(x) = 1\) y\(–1 \leq x \leq 2\). |
| 7. \(f(x) = x^2 + 3 \),\(g(x) = 1 + x\) y\(0 \leq x \leq 3\). |
| 8. \(f(x) = x^2 \),\(g(x) = x\) y\(0 \leq x \leq 2\). |
| 9. \(f(x) = (x –1)^2 \),\(g(x) = x + 1\) y\(0 \leq x \leq 3\). |
| 10. \(f(x) = \frac{1}{x}\),\(g(x) = x\) y\(1 \leq x \leq e\). |
| 11. \(f(x) = \sqrt{x}\),\(g(x) = x\) y\(0 \leq x \leq 4\). |
| 12. \(f(x) = 4 – x^2 \),\(g(x) = x + 2\) y\(0 \leq x \leq 2\). |
| 13. \(f(x) = e^x\),\(g(x) = x\) y\(0 \leq x \leq 2\). |
| 14. \(f(x) = 3 \),\(g(x) = \sqrt{1-x^2}\) y\(0 \leq x \leq 1\). |
| 15. \(f(x) = 2 \),\(g(x) = \sqrt{4-x^2}\) y\(–2 \leq x \leq 2\). |
Para los problemas 16-18, encuentre el volumen del sólido obtenido rotando la región especificada alrededor del\(x\) eje.
16. Región bajo\(f(x) = x^2 + 3\) para\(–1 \leq x \leq 2\).
17. Región bajo\(f(x) = 4 – x^2\) para\(0 \leq x \leq 2\).
18. Región bajo\(f(x) = \frac{1}{x}\) para\(1 \leq x \leq 2\).
En los problemas 19 y 20 utilizan los valores de la tabla para estimar los valores promedio.
| \(x\) | \(f(x)\) | \(g(x)\) |
|
0 |
5 |
2 |
|
1 |
6 |
1 |
|
2 |
6 |
2 |
|
3 |
4 |
2 |
|
4 |
3 |
3 |
|
5 |
2 |
4 |
|
6 |
2 |
0 |
19. Estimar el valor promedio de\(f\) en el intervalo [0, 6].
20. Estimar el valor promedio de\(g\) en el intervalo [0, 6].
En los problemas 21 — 26, encuentra el valor promedio de\(f\) en el intervalo dado.
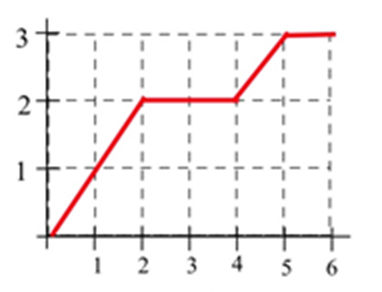
21. \(f(x)\)de la gráfica para\(0 \leq x \leq 2\).
22. \(f(x)\)de la gráfica para\(0 \leq x \leq 4\).
23. \(f(x)\)de la gráfica para\(1 \leq x \leq 6\).
24. \(f(x)\)de la gráfica para\(4 \leq x \leq 6\).
25. \(f(x) = 2x + 1\)para\(0 \leq x \leq 4\).
26. \(f(x) = x^2\)para\(0 \leq x \leq 2\).
El gráfico muestra la velocidad de un automóvil durante un viaje de 5 horas.
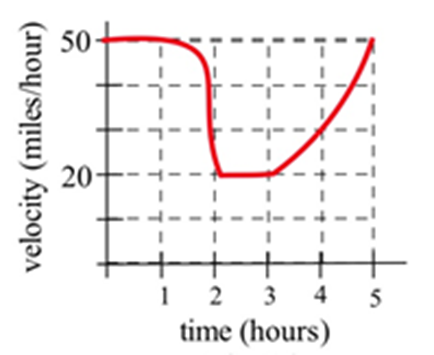
a) Estimar hasta dónde viajó el automóvil durante las 5 horas.
(b) ¿A qué velocidad constante debe conducir para recorrer la misma distancia en 5 horas?
El gráfico muestra el número de llamadas telefónicas por minuto en una compañía grande.
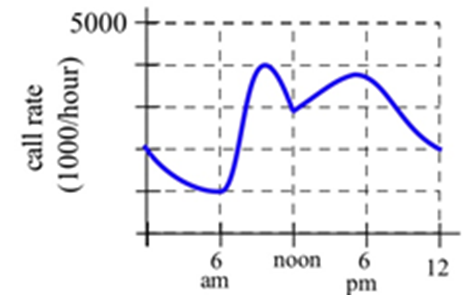
Estimar el número promedio de llamadas por minuto
a) De 8 de la mañana a 5 de la tarde.
b) De las 9 de la mañana a la 1 de la tarde.
3.7 Ejercicios
Las funciones de demanda y oferta para un determinado producto están dadas por\(p = 150 - .5q\) y\(p = .002q^2+1.5\), donde\(p\) está en dólares y\(q\) es el número de artículos.
a) ¿Cuál es la función de demanda?
b) Encontrar el precio y la cantidad de equilibrio
(c) Encontrar las ganancias totales del comercio al precio de equilibrio.
Aún pensando en el producto del Ejercicio 1, con sus funciones de demanda y oferta, supongamos que el precio se fija artificialmente en 70 dólares (que está por encima del precio de equilibrio).
(a) Encontrar la cantidad suministrada y la cantidad demandada a este precio.
b) Calcular el excedente del consumidor a este precio, utilizando la cantidad demandada.
c) Calcular el excedente del productor a este precio, utilizando la cantidad demandada (¿por qué?).
(d) Encontrar las ganancias totales del comercio a este precio.
e) ¿Qué observa?
Cuando el precio de un determinado producto es de $40, se pueden vender 25 artículos. Cuando el precio del mismo producto cuesta $20, se pueden vender 185 artículos. Por otro lado, cuando el precio de este producto sea de $40, se producirán 200 artículos. Pero cuando el precio de este producto sea de $20, solo se producirán 100 artículos. Utilice esta información para encontrar funciones de oferta y demanda (asumir por simplicidad que las funciones son lineales), y calcular el excedente de consumidor y productor al precio de equilibrio.
Encuentre los valores presentes y futuros de un flujo continuo de ingresos de $5000 anuales durante 12 años si el dinero puede ganar 1.3% de interés anual compuesto continuamente.
Encuentre el valor actual de un flujo de ingresos continuo de $40.000 por año durante 35 años si el dinero puede ganar
a) 0.8% de interés anual, compuesto continuamente,
b) 2.5% de interés anual, compuesto continuamente,
c) 4.5% de interés anual, compuesto continuamente.
Encuentra el valor actual de un flujo continuo de ingresos\(F(t) = 20+t\), donde\(t\) está en años y\(F\) está en decenas de miles de dólares al año, por 10 años, si el dinero puede ganar 2% de interés anual, compuesto continuamente.
Encuentra el valor actual de un flujo continuo de ingresos\(F(t) = 12+0.3t^t\), donde\(t\) está en años y\(F\) está en miles de dólares al año, por 8 años, si el dinero puede ganar 3.7% de interés anual, compuesto continuamente.
Encuentra el valor futuro de un flujo continuo de ingresos\(F(t) = 8500+ \sqrt{640t+100}\), donde\(t\) está en años y\(F\) está en dólares al año, por 15 años, si el dinero puede ganar 6% de interés anual, compuesto continuamente.
Se espera que un negocio genere ingresos a una tasa continua de $25,000 anuales para los próximos ocho años. El dinero puede ganar 3.4% de interés anual, compuesto continuamente. El negocio está a la venta por $153,000. ¿Esto es un buen trato?
3.8 Ejercicios
En los problemas 1 — 4, comprobar que la función\(y\) es una solución de la ecuación diferencial dada.
| 1. \(y' + 3y = 6\). \(y = e^{–3x} + 2\). | 2. \(y' – 2y = 8\). \(y = e^{2x} – 4\). |
| 3. \(y' = – x/y\). \(y = \sqrt{7-x^2}\). | 4. \(y' = x – y\). \(y = x – 1 + 2e^{–x}\). |
En los problemas 5 — 8 comprobar que la función\(y\) es una solución del problema de valor inicial dado.
5. \(y' = 6x^2 – 3\)y\(y(1) = 2 \). \(y = 2x^3 – 3x + 3\).
6. \(y' = 6x + 4\)y\(y(2) = 3\). \(y = 3x^2 + 4x – 17\).
7. \(y' = 5y\)y\(y(0) = 7\). \(y = 7e^{5x}\).
8. \(y' = –2y\)y\(y(0) = 3\). \(y = 3e^{–2x}\).
En los problemas 9 — 12, se da una familia de soluciones de una ecuación diferencial. Encuentre el valor de la constante\(C\) para que la solución satisfaga la condición de valor inicial.
| 9. \(y' = 2x\)y\(y(3) = 7\). \(y = x^2 + C\). | 10. \(y' = 3x^2 – 5\)y\(y(1) = 2\). \(y = x^3 – 5x + C\). |
| 11. \(y' = 3y\)y\(y(0) = 5\). \(y = Ce^{3x}\). | 12. \(y' = –2y\)y\(y(0) = 3\). \(y = Ce^{–2x}\). |
En los problemas 13 — 18, resolver la ecuación diferencial. (Supongamos que\(x\) y\(y\) están restringidos para que no se produzca la división por cero.)
| 13. \(y' = 2xy\) | 14. \(y' = x/y\) | 15. \(xy' = y + 3\) |
| 16. \(y' = x^2y + 3y\) | 17. \(y' = 4y\) | 18. \(y' = 5(2 – y)\) |
En los problemas 19 — 22, resolver las ecuaciones diferenciales separables del valor inicial.
19. \(y' = 2xy\)para\(y(0) = 3\),\(y(0) = 5\), y\(y(1) = 2\).
20. \(y' = x/y\)para\(y(0) = 3\),\(y(0) = 5\), y\(y(1) = 2\).
21. \(y' = 3y\)para\(y(0) = 4\),\(y(0) = 7\), y\(y(1) = 3\).
22. \(y' = –2y\)para\(y(0) = 4\),\(y(0) = 7\), y\(y(1) = 3\).
La tasa de crecimiento de una población\(P(t)\) que inicia con 3,000 personas y aumenta 4% anual es\(P '(t) = 0.0392 \cdot P(t)\). Resolver la ecuación diferencial y utilizar la solución para estimar la población en 20 años.
Es la tasa de crecimiento de una población\(P(t)\) que inicia con 5,000 personas y aumenta 3% anual\(P '(t) = 0.0296 \cdot P(t)\). Resolver la ecuación diferencial y utilizar la solución para estimar la población en 20 años.
Un fabricante estima que puede vender un máximo de 130 mil celulares en una ciudad. Al anunciarse fuertemente, sus ventas totales crecen a un ritmo proporcional a la distancia por debajo de este límite superior. Si entra en un nuevo mercado, y después de 6 meses sus ventas totales son 59 mil teléfonos, encuentre una fórmula para las ventas totales (en miles)\(t\) meses después de ingresar al mercado, y utilícela para estimar las ventas totales al final del primer año.
La temperatura de un pavo en el horno crecerá como un crecimiento limitado. El pavo comienza a 40 grados Fahrenheit, y se coloca en un horno de 350 grados. Después de 30 minutos, la temperatura del pavo ha subido a 55 grados. ¿Cuánto tiempo pasará hasta que la temperatura del pavo alcance los 165 grados?
Se introduce en el mercado un nuevo celular. Se prevé que las ventas crecerán logísticamente. El fabricante estima que pueden vender un máximo de 100 mil celulares. Después de que se hayan vendido 44 mil celulares, las ventas están aumentando en 4 mil teléfonos mensuales. Utilice esto para estimar las ventas totales al final del primer año.
Los biólogos abastecieron un lago con 400 peces y estimaron que la capacidad de carga del lago era de 8000 peces. El número de peces se triplicó en el primer año. ¿Cuánto tiempo tardará la población en aumentar a 4000?


