Apéndice A: Relaciones
- Page ID
- 112599
A.1: Relaciones como Juegos de Pares Ordenados
A.1.1: La relación de una función
Ejercicio\(328\)
Considerar las funciones desde\(S = \{−2, −1, 0, 1, 2\}\) hasta\(T = \{1, 2, 3, 4, 5\}\) definidas por\(f(x) = x + 3\), y\(g(x) = x^5 − 5x^3 + 5x + 3\). Anote el conjunto de pares ordenados\((x, f(x))\) para\(x ∈ S\) y el conjunto de pares ordenados\((x, g(x))\) para\(x ∈ S\). ¿Las dos funciones son iguales o diferentes?
El problema 328 señala cómo dos funciones que parecen ser diferentes son en realidad las mismas en algún dominio de interés para nosotros. La mayoría de las veces cuando estamos pensando en funciones está bien pensar en una función casualmente como una relación entre dos conjuntos. En el Problema 328 el conjunto de pares ordenados que anotó para cada función se llama la relación de la función. Cuando queremos distinguir entre lo casual y lo cuidadoso al hablar de relaciones, nuestro término casual será “relación” y nuestro término cuidadoso será “relación”. Entonces relación es una palabra técnica en matemáticas, y como tal tiene una definición técnica. Una relación de un conjunto\(S\) a un conjunto\(T\) es un conjunto de pares ordenados cuyos primeros elementos están en S y cuyos segundos elementos están en\(T\). Otra forma de decir esto es que una relación de\(S\) a\(T\) es un subconjunto de\(S × T\).
Una forma típica de definir una función\(f\) desde un conjunto\(S\), llamado dominio de la función, a un conjunto\(T\), llamado rango, es que\(f\) es una relación entre\(S\) a la\(T\) que relaciona uno y solo un miembro de\(T\) a cada elemento de\(X\). Solemos\(f(x)\) representar el elemento de\(T\) que está relacionado con el elemento\(x\) de\(S\). Si quisiéramos hacer nuestra definición más precisa, podríamos sustituir la palabra “relación” por la palabra “relación” y tendríamos una definición más precisa. Para nuestros fines, puede elegir la definición que prefiera. Sin embargo, en cualquier caso, existe una relación asociada a cada función. Como dijimos anteriormente, la relación de una función\(f: S → T\) (que es la taquigrafía estándar para “\(f\)es una función de\(S\) a\(T\)” y generalmente se lee como\(f\) mapas\(S\) a\(T\)) es el conjunto de todos los pares ordenados\((x, f(x))\) tal que\(x\) es en\(S\).
Ejercicio\(329\)
Aquí hay algunas preguntas que te ayudarán a acostumbrarte a la idea formal de una relación y a la idea formal relacionada de una función. \(S\)representará un conjunto de tamaño\(s\) y\(T\) representará un conjunto de tamaño\(t\).
a. ¿Cuál es el tamaño de la relación más grande de\(S\) a\(T\)?
b. ¿Cuál es el tamaño de la relación más pequeña de\(S\) a\(T\)?
c. La relación de una función\(f: S → T\) es el conjunto de todos los pares ordenados\((x, f(x))\) con\(x ∈ S\). ¿Cuál es el tamaño de la relación de una función de\(S\) a\(T\)? Es decir, ¿cuántos pares ordenados hay en la relación de una función de\(S\) a\(T\)? (Pista).
d. Decimos que\(f\) es una función uno a uno o inyección de\(S\) a\(T\) si cada miembro de\(S\) está relacionado con un elemento diferente de\(T\). ¿Cuántos elementos diferentes deben aparecer como segundos elementos de los pares ordenados en la relación de una función uno a uno (inyección) de\(S\) a\(T\)?
e. Una función\(f: S → T\) se llama una función onto o surjección si cada elemento de\(T\) es\(f(x)\) para algunos\(x ∈ S\) ¿Cuál es el tamaño mínimo que\(S\) puede tener si hay una sobrejección de\(S\) a\(T\)?
Ejercicio\(330\)
Cuando\(f\) es una función de\(S\) a\(T\), los conjuntos\(S\) y\(T\) juegan un papel importante en la determinación de si una función es uno a uno o sobre (como se define en el Problema 329). Para el resto de este problema, dejar\(S\) y\(T\) representar el conjunto de números reales no negativos.
a. Si\(f: S → T\) es dado por\(f(x) = x^2\), ¿es\(f\) uno a uno? ¿Está\(f\) onto?
b. Ahora asuma\(S′\) es el conjunto de todos los números reales y\(g : S′ → T\) está dado por\(g(x) = x^2\). ¿Es\(g\) uno a uno? ¿Está\(g\) onto?
c. Supongamos que\(T′\) es el conjunto de todos los números reales y\(h : S → T′\) está dado por\(h(x) = x^2\). ¿Es\(h\) uno a uno? ¿Está\(h\) onto?
d. Y si la función\(j : S′ → T′\) viene dada por\(j(x) = x^2\), ¿es\(j\) uno a uno? ¿Está\(j\) onto?
Ejercicio\(331\)
Si\(f : S → T\) es una función, decimos que se\(f\) mapea\(x\)\(y\) como otra forma de decir eso\(f(x) = y\). Supongamos\(S = T = \{1, 2, 3\}\). Dar una función de\(S\) a\(T\) que no está en. Observe que dos miembros diferentes de\(S\) han mapeado al mismo elemento de\(T\). Así, cuando decimos que\(f\) asocia uno y solo un elemento de\(T\) a cada elemento de\(S\), es muy posible que el único y único elemento\(1\) al\(f(1)\) que se\(f\) mapea sea exactamente el mismo que el único y único elemento\(f(2)\) que\(f\) mapea \(2\)a.
A.1.2: Gráficas dirigidas
Visualizamos funciones numéricas como\(f(x) = x^2\) con sus gráficas en sistemas de coordenadas cartesianas. Llamaremos a este tipo de gráficas gráficas coordinadas para distinguirlas de otras clases de gráficas utilizadas para visualizar relaciones que no son numéricas.
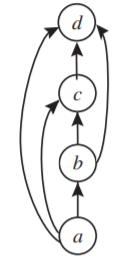
En la Figura A.1.2.1, ilustramos otro tipo de gráfica, una “gráfica dirigida” o “dígrafo” de la relación “viene antes en orden alfabético” en las letras\(a\),\(b\),\(c\), y\(d\). Para dibujar una gráfica dirigida de una relación en un conjunto\(S\), dibujamos un círculo (o punto, si lo preferimos), que llamamos vértice, para cada elemento del conjunto, usualmente etiquetamos el vértice con el elemento conjunto al que corresponde, y dibujamos una flecha desde el vértice\(a\) para eso porque\(b\) si\(a\) está relacionado con\(b\), es decir, si el par ordenado\((a, b)\) está en nuestra relación. Llamamos a tal flecha un borde o un borde dirigido. Dibujamos la flecha desde\(a\) hasta\(b\), por ejemplo, porque\(a\) viene antes\(b\) en orden alfabético. Intentamos elegir las ubicaciones donde dibujamos nuestros vértices para que las flechas capturen lo que estamos tratando de ilustrar lo mejor posible. A veces esto implica redibujar nuestra gráfica dirigida varias veces hasta que pensamos que las flechas capturan bien la relación.
También dibujamos dígrafos para relaciones de un conjunto\(S\) a un conjunto\(T\); simplemente dibujamos vértices para los elementos de\(S\) (generalmente en una fila) y vértices para los elementos de\(T\) (generalmente en una fila paralela) dibujar una flecha de\(x\) adentro\(S\) a\(y\) in\(T\) if \(x\)está relacionado con\(y\). Observe que en lugar de referirnos al vértice que representa\(x\), simplemente nos referimos\(x\). Esta es una taquigrafía común. Aquí hay algunos ejercicios solo para practicar dibujo dígrafos.
Ejercicio\(332\)
Dibuja el dígrafo de la relación “es un subconjunto apropiado de” en el conjunto de subconjuntos de un conjunto de dos elementos. ¿Cuántas flechas habrías tenido que dibujar si este problema te pidiera dibujar el dígrafo para los subconjuntos de un conjunto de tres elementos? (Pista).
También dibujamos dígrafos para relaciones desde un conjunto finito\(S\) a un conjunto finito\(T\); simplemente dibujamos vértices para los elementos de\(S\) (generalmente en una fila) y vértices para los elementos de\(T\) (generalmente en una fila paralela) y dibujamos una flecha de\(x\) adentro\(S\) a\(y\) adentro \(T\)si\(x\) está relacionado con\(y\). Observe que en lugar de referirnos al vértice que representa\(x\), simplemente nos referimos\(x\). Esta es una taquigrafía común.
Ejercicio\(333\)
Dibuja el dígrafo de la relación del conjunto\(\{\text{A, M, P, S}\}\) al conjunto\(\{\text{Sam, Mary, Pat, Ann, Polly, Sarah}\}\) dado por “es la primera letra de”.
Ejercicio\(334\)
Dibuja el dígrafo de la relación del conjunto\(\{\text{Sam, Mary, Pat, Ann, Polly, Sarah}\}\) al conjunto\(\{\text{A, M, P, S}\}\) dado por “tiene como primera letra”.
Ejercicio\(335\)
Dibuja el dígrafo de la relación en el conjunto\(\{\text{Sam, Mary, Pat, Ann, Polly, Sarah}\}\) dado por “tiene la misma primera letra que”.
A.1.3: Dígrafos de Funciones
Ejercicio\(336\)
Cuando dibujamos el dígrafo de una función\(f\), dibujamos una flecha desde el vértice que representa\ (x) al vértice que representa\ (f (x). Una de las relaciones que consideraste en Problemas 333 y Problema 334 es la relación de una función.
a. ¿Qué relación es la relación de una función?
b. ¿Cómo ayuda el dígrafo a visualizar que una relación es una función y la otra no lo es?
Ejercicio\(337\)
Los dígrafos de funciones nos ayudan a visualizar si están o no sobre o uno a uno. Por ejemplo, dejar ambos\(S\) y\(T\) ser el conjunto\(\{−2, −1, 0, 1, 2\}\) y dejar\(S′\) y\(T′\) ser el conjunto\(\{0, 1, 2\}\). Vamos\(f(x)=2 − |x|\).
a. Dibuja el dígrafo de la función\(f\) asumiendo que su dominio es\(S\) y su rango es\(T\). Utilice el dígrafo para explicar por qué o por qué no se\(S\) mapea esta función\(T\).
b. Utilice el dígrafo de la parte anterior para explicar si la función es o no uno a uno.
c. Dibujar el dígrafo de la función\(f\) asumiendo que su dominio es\(S\) y su rango es\(T′\). Usa el dígrafo para explicar si la función está o no.
d. Utilice el dígrafo de la parte anterior para explicar si la función es o no uno a uno.
e. Dibujar el dígrafo de la función\(f\) asumiendo que su dominio es\(S′\) y su rango es\(T′\). Use el dígrafo para explicar si la función está en.
f. Utilice el dígrafo de la parte anterior para explicar si la función es uno a uno.
g. Supongamos que la función\(f\) tiene dominio\(S′\) y rango\(T\). Dibuja el dígrafo de\(f\) y úsalo para explicar si\(f\) está en.
h. Utilizar el dígrafo de la parte anterior para explicar si\(f\) es uno a uno.
Una función uno a uno de un\(X\) conjunto a un conjunto\(Y\) se llama frecuentemente bection, especialmente en combinatoria. Tu trabajo en Problema 337 debería mostrarte que un dígrafo es el dígrafo de una bección desde\(X\) hasta\(Y\)
- si los vértices del dígrafo representan los elementos de\(X\) y\(Y\),
- si cada vértice que representa un elemento de\(X\) tiene una y solo una flecha dejándolo, y
- cada vértice que representa un elemento de\(Y\) tiene una y sólo una flecha entrando en él.
Ejercicio\(338\)
Si invertimos todas las flechas en el dígrafo de una bección\(f\), obtenemos el dígrafo de otra función\(g\). ¿Es\(g\) una beccion? ¿Qué es\(f(g(x))\)? ¿Qué es\(g(f(x))\)?
Si\(f\) es una función de\(S\) a\(T\), si\(g\) es una función de\(T\) a\(S\), y si\(f(g(x)) = x\) para cada\(x\) en\(T\) y\(g(f(x)) = x\) para cada\(x\) en\(S\), entonces decimos que\(g\) es una inversa de\(f\) (y\(f\) es una inversa de\(g\)).
Más generalmente, si\(f\) es una función de un conjunto\(R\) a un conjunto\(S\), y\(g\) es una función de\(S\) a\(T\), entonces definimos una nueva función\(f ◦ g\), llamada la composición de\(f\) y\(g\), por\(f ◦ g(x) = f(g(x))\). La composición de funciones es una operación particularmente importante en sujetos como el cálculo, donde representamos una función\(h(x) = \sqrt{x^2 + 1}\) como la composición de la función de raíz cuadrada y el cuadrado y agregamos una función para usar la regla de cadena para tomar la derivada de\(h\).
La función\(ι\) (la letra griega iota se pronuncia eye-oh-ta) de un conjunto\(S\) a sí mismo, dada por la regla\(ι(x) = x\) para cada\(x\) entrada\(S\), se llama la función de identidad on\(S\). Si\(f\) es una función de\(S\) a\(T\) y\(g\) es una función de\(T\) a\(S\) tal que\(g(f(x)) = x\) para cada\(x\) en\(S\), podemos expresar esto diciendo que\(g ◦ f = ι\), donde\(ι\) esta la función de identidad de\(S\). Decir eso\(f(g(x)) = x\) es lo mismo que decir eso\(f ◦ g = ι\), donde\(ι\) representa la función de identidad en\(T\). Usamos la misma letra para la función de identidad en dos conjuntos diferentes cuando podemos usar contexto para decirnos en qué conjunto se está definiendo la función de identidad.
Ejercicio\(339\)
Si\(f\) es una función de\(S\) a\(T\) y\(g\) es una función de\(T\) a\(S\) tal que\(g(f(x)) = x\), ¿cómo podemos decir desde el contexto que\(g ◦ f\) es la función de identidad\(S\) y no la función de identidad en\(T\)? (Pista).
Ejercicio\(340\)
Explique por qué una función que tiene una inversa debe ser una bection.
Ejercicio\(341\)
¿Es cierto que la inversa de una beccion es una beccion?
Ejercicio\(342\)
Si\(g\) y\(h\) son inversas de\(f\), entonces ¿qué podemos decir sobre\(g\) y\(h\)?
Ejercicio\(343\)
Explique por qué una beccion debe tener una inversa.
Dado que una función con una inversa tiene exactamente una inversa\(g\), llamamos a\(g\) la inversa de\(f\). A partir de ahora, cuando\(f\) tenga un inverso, denotaremos su inverso por\(f −1\). Así\(f(f −1(x)) = x\) y\(f −1(f(x)) = x\). Equivalentemente,\(f ◦ f −1 = ι\) y\(f −1 ◦ f = ι\).
A.2: Relaciones de equivalencia
Hasta ahora hemos utilizado las relaciones principalmente para hablar de funciones. Hay otro tipo de relación, llamada relación de equivalencia, que surge en los problemas de conteo con los que comenzamos. En el Problema 8 con tres sabores distintos, probablemente fue tentador decir que hay\(12\) sabores para la primera pinta,\(11\) para la segunda, y\(10\)) para la tercera, así que hay\(12 · 11 · 10\) formas de elegir las pintas de helado. No obstante, una vez que las pintas han sido elegidas, compradas y puestas en una bolsa, no hay forma de decir cuál es la primera, cuál es la segunda y cuál es la tercera. Lo que acabamos de contar son listas de tres sabores distintos: funciones uno a uno desde\(\{1, 2, 3\}\) el set hasta el conjunto de sabores de helado. Dos de esas listas se convierten en equivalentes una vez que se realiza la compra del helado si listan el mismo helado. En otras palabras, dos de esas listas se vuelven equivalentes (están relacionadas) si enumeran el mismo subconjunto del conjunto de sabores de helado. Para visualizar esta relación con un dígrafo, necesitaríamos un vértice para cada una de las\(12 · 11 · 10\) listas. Incluso con cinco sabores de helado, necesitaríamos un vértice para cada una de\(5·4·3 = 60\) las listas. Entonces por ahora trabajaremos con la cuestión más fácil de dibujar de elegir tres pintas de helado de diferentes sabores a partir de cuatro sabores de helado.
Ejercicio\(344\)
Supongamos que tenemos cuatro sabores de helado, V (anilla), C (hocolate), S (trawberry) y P (cada uno). Dibuja la gráfica dirigida cuyos vértices consten de todas las listas de tres sabores distintos del helado, y cuyos bordes conectan dos listas si listan los mismos tres sabores. Esta gráfica deja bastante claro en cuántas formas podemos elegir\(3\) sabores de cuatro. ¿Cuántos es?
\(\rightarrow\) Exercise \(345\)
Ahora supongamos nuevamente que estamos eligiendo tres sabores distintos de helado de cuatro, pero en lugar de poner las bolas en un cono o elegir pintas, vamos a tener las tres bolas dispuestas simétricamente en un platillo circular. De manera similar a elegir tres pintas, podemos describir una selección de helados en términos de cuál va uno en el platillo primero, cuál va en segundo (digamos a la derecha de la primera), y cuál va en tercero (digamos a la derecha de la segunda primicia, que la hace a la izquierda de la primera primicia). Pero nuevamente, dos de estas listas a veces serán equivalentes. Una vez que están en el platillo, no podemos decir cuál entró primero. Sin embargo, existe una sutil diferencia entre poner cada sabor en su propio platillo pequeño y poner los tres sabores en un círculo en un platillo más grande. Piensa en lo que hace equivalentes las listas de sabores, y dibuja la gráfica dirigida cuyos vértices consten de todas las listas de tres de los sabores del helado y cuyos bordes conectan dos listas que no podemos distinguir entre como platillos de helado. ¿Cuántos platillos de helado podemos distinguir unos de otros? (Pista).
Ejercicio\(346\)
Dibuja el dígrafo para Problema 38 en el caso especial donde tenemos a cuatro personas sentadas alrededor de la mesa.
En Problemas 344, 345 y 346 (así como Problemas 34, 38 y 39) podemos comenzar con un conjunto de listas, y decir cuando dos listas son equivalentes como representaciones de los objetos que estamos tratando de contar. En particular, en Problemas 344, 345 y 346 dibujó la gráfica dirigida para esta relación de equivalencia. Técnicamente, deberías haber tenido una flecha de cada vértice (lista) hacia sí mismo. Esto es lo que queremos decir cuando decimos que una relación es reflexiva. Siempre que tenías una flecha de un vértice a un segundo, tenías una flecha de regreso al primero. Esto es lo que queremos decir cuando decimos que una relación es simétrica.
Cuando las personas se sientan alrededor de una mesa redonda, cada lista es equivalente a sí misma: si List1 y Lista 2 son idénticas, entonces todos tienen la misma persona a la derecha en ambas listas (incluyendo la primera persona en la lista que está a la derecha de la última persona). Para ver la propiedad simétrica de la equivalencia de los arreglos de asientos, si List1 y List2 son diferentes, pero todos tienen la misma persona a la derecha cuando se sientan de acuerdo con List2 que cuando se sientan según List1, entonces es mejor que todos tengan la misma persona a la derecha cuando se sientan de acuerdo con List1 como cuando se sientan según List2.
En Problemas 344, 345 y 346 hay otra propiedad de esas relaciones que quizás hayas notado de la gráfica dirigida. Siempre que tenías una flecha de\(L_1\) a\(L_2\) y una flecha de\(L_2\) a\(L_3\), entonces había una flecha de\(L_1\) a\(L_3\). Esto es lo que queremos decir cuando decimos que una relación es transitiva. También, sin duda, se dio cuenta de cómo la gráfica dirigida se divide en grupos de vértices mutuamente conectados. De esto se tratan las relaciones de equivalencia. Seamos un poco más precisos en nuestra descripción de lo que significa que una relación sea reflexiva, simétrica o transitiva.
- Si\(R\) es una relación en un set\(X\), decimos que\(R\) es reflexivo si\((x, x) ∈ R\) para cada uno\(x ∈ X\).
- Si\(R\) es una relación en un conjunto\(X\), decimos que\(R\) es simétrico si\((x, y)\) está en\(R\) cada vez que\((y, x)\) está en\(R\).
- Si\(R\) es una relación en un set\(X\), decimos que\(R\) es transitivo si cada vez que\((x, y)\) está adentro\(R\) y\((y, z)\) está adentro\(R\), entonces\((x, z)\) está\(R\) adentro también.
Cada una de las relaciones de equivalencia con las que trabajó en Problemas 344, 345 y 346 tenía estas tres propiedades. ¿Se pueden visualizar las mismas tres propiedades en las relaciones de equivalencia que usaría en los Problemas 34, 38 y 39? Llamamos a una relación una relación de equivalencia si es reflexiva, simétrica y transitiva.
Después de algunos ejemplos más, veremos cómo mostrar que las relaciones de equivalencia tienen el tipo de propiedad aglomerante que viste en las gráficas dirigidas. En nuestro primer ejemplo, usar la notación\((a, b) ∈ R\) para decir que\(a\) está relacionado con lo que\(B\) se va a poner en el camino. Realmente es más común escribir\(aRb\) para significar que a está relacionado con\(b\). Por ejemplo, si nuestra relación es la relación menor que en\(\{1, 2, 3\}\), es mucho más probable\(x < y\) que uses de lo que eres\((x, y) ∈ <\), ¿no? La ley reflexiva dice entonces\(xRx\) para cada\(x\) en\(X\), la ley simétrica dice que si\(xRy\), entonces\(yRx\), y la ley transitiva dice que si\(xRy\) y\(yRz\), entonces\(xRz\).
Ejercicio\(347\)
Para el problema del collar, Problema 43, nuestras listas son listas de cuentas. ¿Qué hace que dos listas sean equivalentes con el propósito de describir un collar? Verificar explícitamente que esta relación de equivalencia sea reflexiva, simétrica y transitiva.
Ejercicio\(348\)
¿Cuál de las propiedades reflexivas, simétricas y transitivas tiene la\(<\) relación sobre los enteros?
Ejercicio\(349\)
Una relación\(R\) sobre el conjunto de pares ordenados de enteros positivos que aprendiste en la escuela primaria en otra notación es la relación que dice\((m, n)\) está relacionada con\((h, k)\) si\(mk = hn\). Demostrar que esta relación es una relación de equivalencia. ¿En qué contexto aprendiste sobre esta relación en la escuela primaria? (Pista).
Ejercicio\(350\)
Otra relación que quizás hayas aprendido en la escuela, tal vez bajo la apariencia de “aritmética de reloj”, es la relación de equivalencia módulo\(n\). Para enteros (positivo, negativo o cero)\(a\) y\(b\), escribimos\(a ≡ b (\text{mod } n)\) para significar que\(a − b\) es un múltiplo entero de\(n\), y en este caso, decimos que\(a\) es congruente con\(b\) módulo\(n\) y escribimos\(a ≡ b (\text{mod } n)\). Mostrar que la relación de módulo de congruencia\(n\) es una relación de equivalencia.
Ejercicio\(351\)
Definir una relación en el conjunto de todas las listas de n enteros distintos elegidos\(\{1, 2,..., n\}\), diciendo que dos listas están relacionadas si tienen los mismos elementos (aunque quizás en un orden diferente) en los primeros\(k\) lugares, y los mismos elementos (aunque quizás en un orden diferente) en los últimos\(n − k\) lugares . Mostrar esta relación es una relación de equivalencia.
Ejercicio\(352\)
Supongamos que\(R\) es una relación de equivalencia sobre un conjunto\(X\) y para cada uno\(x ∈ X\), vamos\(C_x = \{y|y ∈ X \text{ and } yRx\}\). Si\(C_x\) y\(C_z\) tienen un elemento\(y\) en común, ¿qué se puede concluir sobre\(C_x\) y\(C_z\) (además del hecho de que tienen un elemento en común!)? Sea explícito sobre qué propiedad (es) de relaciones de equivalencia justifican su respuesta. ¿Por qué cada elemento de\(X\) en algún conjunto\(Cx\)? Sea explícito sobre qué propiedad (es) de las relaciones de equivalencia está utilizando para responder a esta pregunta. Observe que podríamos denotar simultáneamente un conjunto por\(C_x\) y\(C_y\). Explique por qué\(C_x\) es la unión de los conjuntos\(X\). Explique por qué dos conjuntos distintos\(C_x\) y\(C_z\) son disjuntos. ¿Qué tienen que ver estos conjuntos con el “agrupamiento” que viste en el dígrafo de Problema 344 y Problema 345?
En el Problema 352 los conjuntos\(C_x\) se denominan clases de equivalencia de la relación de equivalencia\(R\). Acabas de demostrar que si\(R\) es una relación de equivalencia del conjunto\(X\), entonces cada elemento de\(X\) está exactamente en una clase de equivalencia de\(R\). Recordemos que una partición de un conjunto\(X\) es un conjunto de conjuntos disjuntos cuya unión es\(X\). Por ejemplo,\(\{1, 3\}, \{2, 4, 6\}, \{5\}\) es una partición del conjunto\(\{1, 2, 3, 4, 5, 6\}\). Así, otra forma de describir lo que probaste en el Problema 352 es la siguiente:
Teorema\(A.2.1\)
Si\(R\) es una relación de equivalencia on\(X\), entonces el conjunto de clases de equivalencia de\(R\) es una partición de\(X\).
Dado que una partición de\(S\) es un conjunto de subconjuntos de\(S\), es común llamar a los subconjuntos en los que particionamos\(S\) los bloques de la partición para que no nos encontremos en la incómoda posición de referirnos a un conjunto y no estar seguros si es el conjunto siendo particionado o uno de los bloques de la partición.
Ejercicio\(353\)
En cada uno de los Problemas 38, Problema 39, Problema 43, Problema 344 y Problema 345, ¿a qué corresponde una clase de equivalencia? (Aquí se esperan cinco respuestas.) (Pista).
Ejercicio\(354\)
Dada la partición\(\{1, 3\}\),\(\{2, 4, 6\}\),\(\{5\}\) del conjunto\(\{1, 2, 3, 4, 5, 6\}\), definir dos elementos de\(\{1, 2, 3, 4, 5, 6\}\) a relacionarse si están en la misma parte de la partición. Es decir, definir estar\(1\) relacionado con\(3\) (y\(1\) y\(3\) cada uno relacionado consigo mismo), definir\(2\)\(2\) y\(4\)\(6\), y,\(4\) y estar\(6\) relacionado (y cada uno de\(2\)\(4\),, y estar\(6\) relacionado consigo mismo) , y\(5\) definir estar relacionado consigo mismo. Demostrar que esta relación es una relación de equivalencia.
Ejercicio\(355\)
Supongamos que\(P = \{S_1, S_2, S_3,..., S_k \}\) es una partición de\(S\). Definir dos elementos de estar\(S\) relacionados si están en el mismo conjunto\(S_i\), y de lo contrario no estar relacionados. Demostrar que esta relación es una relación de equivalencia. Mostrar que las clases de equivalencia de la relación de equivalencia son los conjuntos\(S_i\).
En Problema 353 acabas de demostrar que cada partición de un conjunto da lugar a una relación de equivalencia cuyas clases son solo las partes de la partición. Así en Problema 352 y Problema 353 probaste el siguiente Teorema.
Teorema\(A.2.2\)
Una relación\(R\) es una relación de equivalencia en un conjunto\(S\) si y sólo si se\(S\) puede dividir\(S_1, S_2,..., S_n\) en conjuntos de tal manera que\(x\) y\(y\) se relacionan por\(R\) si y sólo si están en el mismo bloque\(S_i\) de la partición.
En Problemas 344, Problema 345, Problema 38 y Problema 43 lo que estábamos haciendo en cada caso era contar clases de equivalencia de una relación de equivalencia. Había una estructura especial a los problemas que hacía que esto fuera algo más fácil de hacer. Por ejemplo, en el Problema 344, teníamos\(4 · 3 · 2 = 24\) listas de tres sabores distintos elegidos entre V, C, S y P. Cada lista era equivalente a\(3 · 2 · 1 = 3! = 6\) listas, incluyéndose a sí misma, desde el punto de vista de servir platillos\(3\) pequeños de helado. El orden en el que seleccionamos los tres sabores no fue importante. Así, el conjunto de todas\(4 · 3 · 2\) las listas fue una unión de algún número\(n\) de clases de equivalencia, cada una de tamaño\(6\). Por el principio del producto, si tenemos una unión de\(n\) conjuntos disjuntos, cada uno de tamaño\(6\), la unión tiene\(6n\) elementos. Pero ya sabíamos que la unión era el conjunto de todas las\(24\) listas de tres letras distintas elegidas de nuestras cuatro letras. Así tenemos\(6n = 24\), o clases de\(n = 4\) equivalencia.
En el Problema 345 hay un cambio sutil. En el lenguaje que adoptamos para sentar a las personas alrededor de una mesa redonda, si elegimos los sabores V, C y S, y los colocamos en el plato con C a la derecha de V y S a la derecha de C, entonces las primicias están en diferentes posiciones relativas que si las arreglamos con S a la derecha de V y C a la derecha de S. Así el orden en que las primicias van al platillo es algo importante —algo, porque poner primero en V, luego C a su derecha y S a su derecha es lo mismo que poner en S primero, luego V a su derecha y C a su derecha. En este caso, cada lista de tres sabores equivale a sólo tres listas, incluyéndose a sí misma, y así si hay n clases de equivalencia, tenemos\(3n = 24\), entonces hay clases de\(\dfrac{24}{3} = 8\) equivalencia.
Ejercicio\(356\)
Si tenemos una relación de equivalencia que divide un conjunto con\(k\) elementos hasta en clases de equivalencia cada una de tamaño\(m\), ¿cuál es el número\(n\) de clases de equivalencia? Explique por qué.
Ejercicio\(357\)
En Problema 347, ¿cuál es el número de clases de equivalencia? Explique con palabras la relación entre este problema y el Problema 39.
Ejercicio\(358\)
Describa explícitamente qué hace que dos listas de cuentas sean equivalentes en el Problema 43 y cómo se puede usar el Problema 356 para calcular el número de collares diferentes.
Ejercicio\(359\)
¿Cuáles son las clases de equivalencia (escríbelas como conjuntos de listas) en el Problema 45, y por qué no podemos usar el Problema 356 para calcular el número de clases de equivalencia?
En Problema 356 probaste nuestro siguiente teorema. En el Capítulo 1 (Problema 42) descubrimos y afirmamos este teorema en el contexto de las particiones y lo llamamos el Principio del Cociente
Teorema\(A.2.3\)
Si una relación de equivalencia en un\(S\) tamaño conjunto\(k\) tiene clases de\(n\) equivalencia cada una de tamaño\(m\), entonces el número de clases de equivalencia es\(k/m\).


