4.3: Minsets

Definición de Minsets

Dejar\(B_1\) y\(B_2\) ser subconjuntos de un conjunto\(A\text{.}\) Observe que el diagrama de Venn de la Figura\(\PageIndex{1}\) está naturalmente dividido en los subconjuntos\(A_1\text{,}\)\(A_2\text{,}\)\(A_3\text{,}\) y\(A_4\text{.}\) Además observamos eso\(A_1\text{,}\)\(A_2\text{,}\)\(A_3\text{,}\) y se\(A_4\) puede describir en términos de\(B_1\) y de\(B_2\) la siguiente manera:

Figura\(\PageIndex{1}\): Venn Diagrama de Minsets

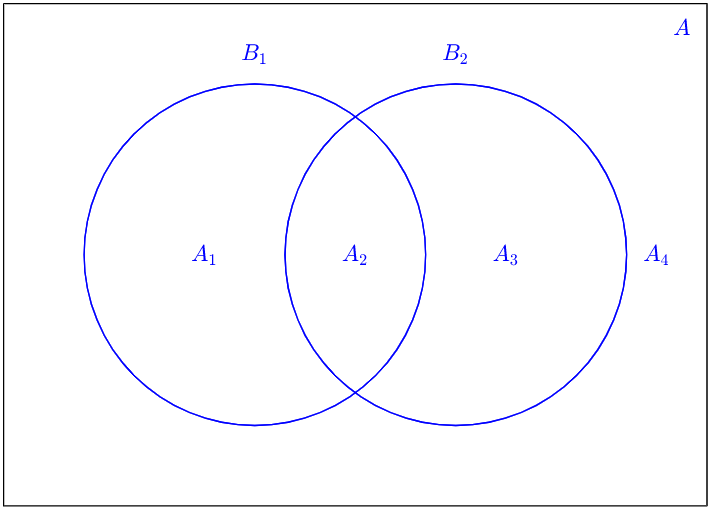
Tabla\(\PageIndex{1}\): Minsets generados por dos conjuntos

\(A_1=B_1\cap B_2^c\)

\(A_2=B_1\cap B_2\)

\(A_3=B_1^C\cap B_2\)

\(A_4=B_1^c\cap B_2^c\)

Cada\(A_i\) is called a minset generado por\(B_1\) and \(B_2\text{.}\) We note that each minset se forma tomando la intersección de dos conjuntos donde cada uno puede ser cualquiera de los\(B_k\) or its complement, \(B_k^c\text{.}\) Note also, given two sets, there are \(2^{2}=4\) minsets.

Ocasionalmente, los minsets se llaman minterms.

El lector debe tener en cuenta que si aplicamos todas las combinaciones posibles de intersección de operaciones, unión y complementación a los conjuntos\(B_1\) y\(B_2\) de Figura\(\PageIndex{1}\), los conjuntos más pequeños generados serán exactamente los minsets, los conjuntos mínimos. De ahí la derivación del término minset.

A continuación, considera el diagrama de Venn que contiene tres conjuntos,\(B_1\text{,}\)\(B_2\text{,}\) y ¡\(B_3\text{.}\)Dibuja ahora mismo y cuenta las regiones! ¿Cuáles son los minsets generados por\(B_1\text{,}\)\(B_2\text{,}\) y\(B_3\text{?}\) cuántos hay? Siguiendo los procedimientos señalados anteriormente, observamos que los siguientes son tres de los\(2^3=8\) minsets. ¿Cuáles son los demás?

Tabla\(\PageIndex{2}\): Tres de las minsets generadas por\(B_1\),\(B_2\), y\(B_3\)

\(B_1\cap B_2\cap B_3^c\)

\(B_1\cap B_2^c\cap B_3\)

\(B_1\cap B_2^c\cap B_3^c\)

Definición \(\PageIndex{1}\): Minset

Dejar\(\{B_1, B_2,\ldots,B_n\}\) ser un conjunto de subconjuntos de\(A\text{.}\) conjuntos conjuntos de la forma\(D_1\cap D_2\cap \cdots \cap D_n\text{,}\) donde cada uno\(D_i\) puede ser\(B_i\) o\(B_i^c\text{,}\) se llama un minset generado por\(B_1\text{,}\)\(B_2\text{,...}\) y\(B_n\text{.}\)

Ejemplo\(\PageIndex{1}\): A Concrete Example of Some Minsets

Considera el siguiente ejemplo concreto. Dejar\(A = \{1, 2, 3, 4, 5, 6\}\) con subconjuntos\(B_1 = \{1,3,5\}\) y\(B_2= \{1,2,3\}\text{.}\) cómo podemos usar operaciones de conjunto aplicadas a y producir una partición de\(A\text{?}\) Como primer intento, podríamos probar estos tres conjuntos:

Mesa\(\PageIndex{3}\)

\(B_1\cap B_2=\{1,3\}\)

\(B_1^c=\{2,4,6\}\)

\(B_2^c=\{4,5,6\}\text{.}\)

Hemos producido todos los elementos de\(A\) pero tenemos 4 y 6 repetidos en dos series. En lugar de\(B_1^c\) y\(B_2^c\text{,}\) vamos a tratar\(B_1^c\cap B_2\) y\(B_1\cap B_2^c\text{,}\) respectivamente:

Mesa\(\PageIndex{4}\)

\(B_1^c\cap B_2=\{2\}\)y

\(B_1\cap B_2^c=\{5\}\text{.}\)

Ahora hemos producido los elementos 1, 2, 3 y 5 usando\(B_1\cap B_2\text{,}\)\(B_1^c\cap B_2\) y\(B_1\cap B_2^c\) sin embargo no hemos enumerado los elementos 4 y 6. La mayoría de las formas en las que podríamos combinar\(B_1\) y\(B_2\) como\(B_1\cup B_2\) o\(B_1\cup B_2^c\) producirán duplicaciones de elementos listados y no producirán tanto 4 como 6. Sin embargo observamos que\(B_1^c\cap B_2^c= \{4, 6\}\text{,}\) exactamente los elementos que necesitamos.

Después de experimentar más, podríamos llegar a la conclusión de que cada elemento de\(A\) aparece exactamente una vez en uno de los cuatro minsets\(B_1\cap B_2\),\(B_1^c\cap B_2\text{,}\)\(B_1\cap B_2^c\) y\(B_1^c\cap B_2^c\text{.}\) por lo tanto, tenemos una partición de\(A\text{.}\) De hecho esta es la partición más fina de\(A\) en que todas las demás particiones nos podría generar consistir en uniones seleccionadas de estos minsets.

En este punto, podríamos preguntar y poder responder a la pregunta “A partir de cuántos subconjuntos diferentes de nuestro universo podemos generar\(B_1\) y\(B_2\text{?}\)” La respuesta es\(2^{\textrm{number of nonempty minsets}}\text{,}\) cual es\(2^4=16\) en este caso. Observe que en general, sería imposible encontrar dos conjuntos a partir de los cuales podríamos generar todos los subconjuntos\(A=\{1, 2, 3, 4, 5, 6\}\) ya que nunca habrá más de cuatro minsets no vacíos. Si nos permitiéramos tres subconjuntos y tratáramos de generar todos los conjuntos a partir de ellos, entonces el número de minsets sería\(2^3 =8\text{.}\) Con solo seis elementos en podría\(A\text{,}\) haber seis minsets, cada uno conteniendo un solo elemento. En ese caso podríamos generar todo el conjunto de potencia de\(A\text{.}\)

Propiedades de Minsets

Teorema\(\PageIndex{1}\): Minset Partition Theorem

Dejar\(A\) ser un conjunto y dejar\(B_1\text{,}\)\(B_2\)\(\ldots\),\(B_n\) ser subconjuntos de\(A\text{.}\) El conjunto de minsets no vacíos generados por\(B_1\text{,}\)\(B_2\)\(\ldots\),\(B_n\) es una partición de\(A\text{.}\)

Prueba

La prueba de este teorema se deja al lector.

Uno de los hechos más significativos sobre minsets es que cualquier subconjunto de los\(A\) que se puede obtener\(B_1\text{,}\)\(B_2\)\(\ldots\text{,}\)\(B_n\text{,}\) usando las operaciones de conjunto estándar se puede obtener en una forma estándar tomando la unión de minsets seleccionados.

Definición \(\PageIndex{2}\): Minset Normal Form

Se dice que un conjunto está en forma normal minset cuando se expresa como la unión de cero o más minsets distintos no vacíos.

Nota\(\PageIndex{1}\)

• La unión de conjuntos cero es el conjunto vacío,\(\emptyset\text{.}\)
• La forma normal de minset también se llama forma canónica.

Ejemplo\(\PageIndex{2}\): Another Concrete Example of Minsets

Let\(U = \{-2,-1,0,1,2\}\text{,}\)\(B_1= \{0,1,2\}\text{,}\) y\(B_2= \{0,2\}\text{.}\) Entonces

Mesa\(\PageIndex{5}\)

\(B_1\cap B_2=\{0,2\}\)

\(B_1^c\cap B_2 = \emptyset\)

\(B_1\cap B_2^c = \{1\}\)

\(B_1^c\cap B_2^c = \{-2,-1\}\)

En este caso, sólo hay tres minsets no vacíos, produciendo la partición\(\{\{0,2\},\{1\},\{-2,-1\}\}\text{.}\) Un ejemplo de un conjunto que no se pudo producir a partir de solo\(B_1\) y\(B_2\) es el conjunto de elementos pares de\(U\text{,}\)\(\{-2,0,2\}\text{.}\) Esto es porque\(-2\) y\(-1\) no se puede separar. Están en el mismo minset y cualquier unión de minsets los incluye o excluye a ambos. En general, hay\(2^3= 8\) diferentes formas normales minset porque hay tres minsets no vacíos. Esto significa que solo 8 de los\(2^5=32\) subconjuntos de\(U\) podrían generarse a partir de dos conjuntos cualesquiera\(B_1\) y\(B_2\text{.}\)

Ejercicios

Ejercicio\(\PageIndex{1}\)

Considere los subconjuntos\(A = \{1, 7, 8\}\text{,}\)\(B = \{1, 6, 9, 10\}\text{,}\) y\(C = \{1, 9, 10\}\text{,}\) dónde\(U = \{1,2, . . . , 10\}\text{.}\)

1. Enumere los minsets no vacíos generados por\(A, B, \textrm{ and } C\text{.}\)
2. Cuántos elementos del conjunto de potencia de\(U\) pueden ser generados por\(A\text{,}\)\(B\text{,}\) y\(C\text{?}\) Comparar este número con\(\mid\mathcal{P}(U)\mid\text{.}\) Dar un ejemplo de un subconjunto que no puede ser generado por\(A\text{,}\)\(B\text{,}\) y\(C\text{.}\)

Contestar

1. \(\displaystyle \{1\}, \{2, 3, 4, 5\}, \{6\}, \{7, 8\}, \{9, 10\}\)
2. \(2^5\), en comparación con\(2^{10}\text{.}\)\(\{1, 2\}\) es uno de los 992 conjuntos que no se pueden generar.

Ejercicio\(\PageIndex{2}\)

1. Partición\(\{1, 2, .... 9\}\) en los minsets generados por\(B_1= \{5, 6,7\}\text{,}\)\(B_2 = \{2, 4, 5, 9\}\text{,}\) y\(B_3 = \{3, 4, 5, 6, 8, 9\}\text{.}\)
2. ¿Cuántos subconjuntos diferentes\(\{1, 2, . . . ,9\}\) se pueden crear usando\(B_1, B_2\text{,}\) y\(B_3\) con las operaciones de conjunto estándar?
3. ¿Existen subconjuntos\(C_1, C_2, C_3\) cuyos minsets generarán cada subconjunto de\(\{1,2, . . . ,9\}\text{?}\)

Ejercicio\(\PageIndex{3}\)

Particionar el conjunto de cadenas de 0 y 1 de longitud dos o menos, usando los minsets generados por\(B_1=\{s \mid s \textrm{ has length } 2\}\text{,}\) y\(B_2= \{s \mid s \textrm{ starts with a } 0\}\text{.}\)

Contestar

\(B_1= \{00, 01, 10, 11\}\)y\(B_2 = \{0, 00, 01\}\) generar minsets\(\{00, 01\}, \{0\}, \{10, 11\}\text{,}\) y\(\{\lambda , 1\}\text{.}\) Nota:\(\lambda\) es la cadena nula, que tiene longitud cero.

Ejercicio \(\PageIndex{4}\)

Dejar\(B_1, B_2\text{,}\) y\(B_3\) ser subconjuntos de un conjunto universal\(U\text{,}\)

1. Listar simbólicamente todos los minsets generados por\(B_1, B_2\text{,}\) y\(B_3\text{.}\)
2. Ilustrar con un diagrama de Venn todos los minsets obtenidos en la parte (a).
3. Exprese los siguientes conjuntos en forma normal minset:\(B_1^c\text{,}\)\(B_1\cap B_2\),\(B_1\cup B_2^c\text{.}\)

Ejercicio\(\PageIndex{5}\)

1. Partición\(A = \{0, 1, 2, 3, 4, 5\}\) con los minsets generados por\(B_1= \{0, 2, 4\}\text{ }\) y\(B_2= \{1, 5\}\text{.}\)
2. ¿Cuántos subconjuntos diferentes\(A\) puedes generar a partir de\(B_1 \textrm{ and } B_2\text{?}\)

Contestar

1. \(B_1\cap B_2=\emptyset\text{,}\) \(B_1\cap B_2^c=\{0,2,4\}\text{,}\) \(B_1^c\cap B_2=\{1,5\}\text{,}\) \(B_1^c\cap B_2^c=\{3\}\)
2. \(2^3\text{,}\)ya que hay 3 minsets no vacíos.

Ejercicio\(\PageIndex{6}\)

Si\(\left\{B_1, B_2, \ldots , B_n\right\}\) es una partición de\(A\text{,}\) cuántos minsets son generados por\(B_1, B_2, \ldots , B_n\text{?}\)

Ejercicio\(\PageIndex{7}\)

Demostrar teorema\(\PageIndex{1}\).

Contestar

Dejar\(a\in A\text{.}\) Para cada uno\(i\text{,}\)\(a\in B_i\text{,}\) o\(a\in B_i{}^c\text{,}\) desde\(B_i\cup B_i{}^c=A\) por la ley del complemento. Dejar\(D_i=B_i\) si\(a\in B_i\text{,}\) y de\(D_i=B_i{}^c\) otra manera. Ya que\(a\) está en cada uno\(D_i\text{,}\) debe estar en el minset\(D_1\cap D_2 \cdots \cap D_n\text{.}\) Ahora considera dos minsets diferentes\(M_1= D_1\cap D_2\cdots \cap D_n\text{,}\) y\(M_2=G_1\cap G_2\cdots \cap G_n\text{,}\) donde cada uno\(D_i\) y\(G_i\) es\(B_i\) o\(B_i{}^c\text{.}\) ya que estos minsets no son iguales,\(D_i\neq G_i\text{,}\) para algunos\(i\text{.}\) Por lo tanto, \(M_1\cap M_2=D_1\cap D_2 \cdots \cap D_n\cap G_1\cap G_2\cdots \cap G_n=\emptyset\text{,}\)ya que dos de los conjuntos en la intersección son disjuntos. Dado que cada elemento de\(A\) está en un minset y los minsets son disjuntos, los minsets no vacíos deben formar una partición de\(A\text{.}\)\(\square\)

Ejercicio\(\PageIndex{8}\)

Let\(S\) Ser un conjunto finito de\(n\) elementos. Dejar\(B_i\text{,}\)\(i = 1, 2, \ldots , k\) ser subconjuntos no vacíos de\(S\text{.}\) Hay\(2^{2^k}\) minset formas normales generadas por los\(k\) subconjuntos. El número de subconjuntos de\(S\) es\(2^n\text{.}\) Dado que podemos hacer\(2^{2^k} > 2^n\) eligiendo está\(k \geq \log _2 n\text{,}\) claro que dos expresiones minset de forma normal distintas no siempre son iguales a subconjuntos distintos de\(S\text{.}\) Incluso\(k < \log _2 n\text{,}\) porque puede suceder que dos expresiones de forma normal minset distintas sean iguales el mismo subconjunto de\(S\text{.}\) Determinar condiciones necesarias y suficientes para que distintas expresiones de forma normal sean iguales a subconjuntos distintos de\(S\text{.}\)