12.5: Algunas aplicaciones

Un gran y variado número de aplicaciones implica cálculos de potencias de matrices. Estas aplicaciones se pueden encontrar en la ciencia, las ciencias sociales, la economía, la ingeniería y, muchas otras áreas donde se utiliza la matemática. Consideraremos algunos ejemplos diversos de las matemáticas detrás de estas aplicaciones aquí.

Diagonalización

Comenzamos desarrollando una técnica útil para la computación$A^m\text{,}$$m > 1\text{.}$ Si se$A$ puede diagonalizar, entonces hay una matriz$P$ tal que$P^{-1}A P = D\text{,}$ donde$D$ está una matriz diagonal y

$$\label{eq:1}A^{m}=PD^{m}P^{-1}\text{ for all }m\geq 1$$

El comprobante de esta identidad fue un ejercicio en la Sección 5.4. La condición de que$D$ sea una matriz diagonal no es necesaria pero cuando lo es, el cálculo en el lado derecho es particularmente fácil de realizar. Si bien la prueba formal se hace por inducción, la razón por la que es verdad se ve fácilmente escribiendo un ejemplo como$m=3\text{:}$

\ begin {ecuación*}\ begin {split} A^3 & =\ izquierda (P D P^ {-1}\ derecha) ^3\\ & =\ izquierda (P D P^ {-1}\ derecha)\ izquierda (P D P^ {-1}\ derecha)\ izquierda (P D P^ {-1}\ derecha)\\ &= P D\ izquierda (P^ {-1} P\ derecha)\ izquierda (P^ {-1} P\ derecha) D P^ {-1}\ quad\ textrm {por asociatividad de multiplicación matricial}\\ &= P D I D I D P^ {-1}\\ &= P D D D P^ {-1}\\ &= P D^3 P^ {-1}\\\ final {división}\ final {ecuación*}

Ejemplo$\PageIndex{1}$: Application to Recursion: Matrix Computation of the Fibonacci Sequence

Considerar el cómputo de términos de la Secuencia de Fibonnaci. Recordemos eso$F_0= 1, F_1= 1$ y$F_k= F_{k-1}+F_{k-2}$ para$k\geq 2\text{.}$

Para formular el cálculo en forma de matriz, introdujimos la “ecuación ficticio”$F_{k-1}= F_{k-1}$ para que ahora tengamos dos ecuaciones

\ begin {ecuación*}\ begin {array} {c} f_k= F_ {k-1} +F_ {k-2}\\ F_ {k-1} = F_ {k-1}\\ end {array}\ end {ecuación*}

Si$A = \left( \begin{array}{cc} 1 & 1 \\ 1 & 0 \\ \end{array} \right)\text{,}$ estas dos ecuaciones se pueden expresar en forma de matriz como

\ begin {ecuación*}\ begin {split}\ left (\ begin {array} {c} F_k\\ F_ {k-1}\\ end {array}\ right) &=\ left (\ begin {array} {cc} 1 & 1\\ 1 & 0\\ end {array}\\ right)\ left (\ begin {array} {c} F_ {k-1}\\ F_ {k-2}\\\ end {array}\ derecha)\ quad\ textrm {if} k\ geq 2\\ &= A\ left (\ begin {array} {c} F_ {k-1}\\ F_ {k- 2}\\\ end {array}\\ derecha)\\ &= A^2\ izquierda (\ begin {array} {c} F_ {k-2}\\ F_ {k-3}\\\ end {array}\ derecha)\ quad\ textrm {if} k\ geq 3\\ & etc.\\\ end {split}\ end {ecuación*}

Podemos usar la inducción para probar que si$k\geq 2\text{,}$

\ begin {ecuación*}\ left (\ begin {array} {c} f_k\\ F_ {k-1}\\\ end {array}\ right) =A^ {k-1}\ left (\ begin {array} {c} 1\\ 1\\ end {array}\ derecha)\ end {equation*}

A continuación, diagonalizando$A$ y usando el hecho de que$A^{m }= P D^m P^{-1}\text{.}$ podemos demostrar que

\ begin {ecuación*} f_k=\ frac {1} {\ sqrt {5}}\ izquierda (\ izquierda (\ frac {1+\ sqrt {5}} {2}\ derecha) ^k-\ izquierda (\ frac {1-\ sqrt {5}} {2}\ derecha) ^k\ derecha)\ end {ecuación*}

Algunos comentarios sobre este ejemplo:

1. Una ecuación de la forma$F_k = a F_{k-1} + b F_{k-2}$, donde$a$ y$b$ se dan constantes, se conoce como una ecuación lineal homogénea de diferencia de segundo orden. Las condiciones$F_0=c_0$ y$F_1= c_1$, donde$c_1$ y$c_2$ son constantes, se denominan condiciones iniciales. Aquellos de ustedes que estén familiarizados con las ecuaciones diferenciales pueden reconocer que este lenguaje es paralelo a lo que se usa en las ecuaciones diferenciales. Las ecuaciones de diferencia (también conocido como recurrencia) avanzan discretamente; es decir, en un número finito de pasos positivos. Por otro lado, una ecuación diferencial se mueve continuamente; es decir, toma un número infinito de pasos infinitesimales.
2. Una relación de recurrencia de la forma$S_k = a S_{k-1} + b\text{,}$ donde$a$ y$b$ son constantes, se denomina ecuación de diferencia de primer orden. Para escribir la secuencia, necesitamos conocer una condición inicial. Ecuaciones de este tipo se pueden resolver de manera similar al método descrito en el ejemplo introduciendo la ecuación$1 =0\cdot F_{k-1}+1$ superflua para obtener en la ecuación matricial:
   \ begin {equation*}\ left (\ begin {array} {c} f_k\\ 1\\ end {array}\ right) =\ left (\ begin {array} {cc} a & b\\ 0 & 1\\\ end {array}\ right)\ left (\ begin {array} {c} S_ {k-1}\\ 1\\ end {array}\ right)\ textrm {}\ Rightarrow\ left (\ begin {array} {c} F_k\\ 1\\ end {array}\\ right) =\ left (\ begin {array} {cc} a & b\ 0 & 1\\\ end {array}\ right) ^k\ left (\ begin {array} {c} F_0\\ 1\\ end {array}\ right)\ end {equation*}

Contando

En el siguiente ejemplo, aplicamos el siguiente teorema, el cual puede ser probado por inducción.

Teorema$\PageIndex{1}$: Path Counting Theorem

Si$A$ es la matriz de adyacencia de una gráfica con vértices$\{v_1, v_2, \dots,v_n\}\text{,}$ entonces la entrada$\left(A^k\right)_{ij}$ es el número de rutas de longitud$k$ de nodo$v_i$ a nodo$v_j\text{.}$

Ejemplo$\PageIndex{2}$: Counting Paths with Diagonalization

Considera la gráfica en la Figura$\PageIndex{1}$.

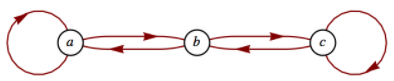Figura$\PageIndex{1}$: Contar números de trayectorias

Como vimos en la Sección 6.4, la matriz de adyacencia de esta gráfica es$A=\left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ \end{array} \right)\text{.}$

Recordemos que$A^k$ es la matriz de adyacencia de la relación$r^k\text{,}$ donde$r$ está la relación$\{(a, a), (a, b), (b, a), (b, c), (c, b), (c, c)\}$ de la gráfica anterior. También recordamos que en la computación$A^k\text{,}$ utilizamos la aritmética booleana. ¿Qué pasa si usamos aritmética “regular”? Si nos$A$ cuadramos obtenemos$A^2 = \left( \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\ \end{array} \right)$

¿Cómo podemos interpretar esto? Observamos que$A_{33} = 2$ y que hay dos caminos de longitud dos de$c$ (el tercer nodo) a$c\text{.}$ También,$A_{13} = 1\text{,}$ y hay una ruta de longitud 2 de$a$ a$c\text{.}$ El lector debe verificar estas afirmaciones examinando la gráfica.

Cómo calculamos$A^k$ para valores posiblemente grandes de A$k\text{?}$ partir de la discusión al inicio de esta sección, sabemos que$A^k= P D^kP^{-1}$ si$A$ es diagonalizable. Dejamos al lector demostrar que$\lambda = 1, 2,\textrm{ and } -1$ son valores propios de$A$ con vectores propios

\ begin {ecuación*}\ left (\ begin {array} {c} 1\\ 0\\ -1\\\ end {array}\ right),\ left (\ begin {array} {c} 1\\ 1\\\ end {array}\\ right),\ textrm {y}\ left (\ begin {array} {c} {c} 1\ -2\ 1\\ final\ {array}\ derecha)\ end {ecuación*}

Entonces

\ begin {ecuación*} a^k= P\ left (\ begin {array} {ccc} 1 & 0 & 0\\ 0 y 2^k & 0\\ 0 & 0 & (-1) ^k\\ end {array}\ derecha) P^ {-1}\ end {ecuación*}

dónde$P=\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & -2 \\ -1 & 1 & 1 \\ \end{array} \right)$ y$P^{-1}=\left( \begin{array}{ccc} \frac{1}{2} & 0 & -\frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \end{array} \right)$

Consulte Ejercicio$\PageIndex{5}$ de esta sección para la realización de este ejemplo.

Cálculo Matriz

Ejemplo$\PageIndex{3}$: Matrix Calculus - Exponentials

Quienes han estudiado el cálculo recuerdan que la serie Maclaurin es una forma útil de expresar muchas funciones comunes. Por ejemplo,$e^x=\sum _{k=0}^{\infty } \frac{x^k}{k!}\text{.}$ Indeed, calculadoras y computadoras utilizan estas series para los cálculos. Dado un polinomio$f(x)\text{,}$ definimos la matriz-polinomio$f(A)$ para matrices cuadradas en el Capítulo 5. De ahí que estemos en condiciones de describir$e^A$ para una$n \times n$ matriz$A$ como límite de polinomios, las sumas parciales de la serie. Formalmente, escribimos

\ begin {ecuación*} e^a= I + A +\ frac {A^2} {2! } +\ frac {A^3} {3!} +\ cdots =\ suma _ {k=0} ^ {\ infty}\ frac {a^k} {k!} \ end {ecuación*}

Nuevamente nos encontramos con la necesidad de computar altas potencias de una matriz. Dejar$A$ ser una matriz$n\times n$ diagonalizable. Entonces existe una$n\times n$ matriz invertible$P$ tal que$P^{-1}A P = D\text{,}$ una matriz diagonal, de modo que

\ begin {ecuación*}\ begin {split} e^a &=e^ {P D P^ {-1}}\\ & =\ sum _ {k=0} ^ {\ infty}\ frac {\ izquierda (P D P^ {-1}\ derecha) ^k} {k!} \\ & = P\ izquierda (\ sum _ {k=0} ^ {\ infty}\ frac {d^k} {k!} \ derecha) P^ {-1}\ end {split}\ end {ecuación*}

La suma infinita en medio de esta expresión final se puede evaluar fácilmente si$D$ es diagonal. Todas las entradas de potencias de la diagonal son cero y la$i^{\textrm{ th}}$ entrada de la diagonal es

\ begin {ecuación*}\ left (\ sum _ {k=0} ^ {\ infty}\ frac {d^k} {k!} \ derecha) {} _ {i i} =\ suma _ {k=0} ^ {\ infty}\ frac {D_ {i i} {} ^k} {k!} = e^ {D_ {ii}}\ final {ecuación*}

Por ejemplo, si$A=\left( \begin{array}{cc} 2 & 1 \\ 2 & 3 \\ \end{array} \right)\text{,}$ la primera matriz la diagonalizamos en la Sección 12.3, encontramos que$P =\left( \begin{array}{cc} 1 & 1 \\ -1 & 2 \\ \end{array} \right)$ y$D= \left( \begin{array}{cc} 1 & 0 \\ 0 & 4 \\ \end{array} \right)\text{.}$

Por lo tanto,

\ begin {ecuación*}\ begin {split} e^a &=\ left (\ begin {array} {cc} 1 & 1\\ -1 & 2\\\ end {array}\ derecha)\ left (\ begin {array} {cc} e & 0\\ 0 & e^4\\\ end {array}\ derecha)\ left (\ begin {array} {cc}\ frac {2} {3} & -\ frac {1} {3}\\ frac {1} {3} &\ frac {1} {3}\\ end {array}\\ derecha)\\ &=\ izquierda ( \ begin {array} {cc}\ frac {2 e} {3} +\ frac {e^4} {3} & -\ frac {e} {3} +\ frac {e^4} {3}\ -\ frac {2 e} {3} +\ frac {2 e^4} {3} &\ frac {e} {3} +\ frac {2 e^4} {3}\\ end {array}\ derecha)\\ &\ approx\ izquierda (\ begin {array} {cc} 20.0116 & 17.2933\\ 34.5866 & 37.3049\\ end {array}\ right)\ end {split}\ end {split}\ end {ecuación*}

Observación$\PageIndex{1}$

Muchas de las ideas de cálculo se pueden desarrollar usando matrices. Por ejemplo, si$A(t) = \left( \begin{array}{cc} t^3 & 3 t^2+8t \\ e^t & 2 \\ \end{array} \right)$ entonces$\frac{d A(t)}{d t}=\left( \begin{array}{cc} 3 t^2 & 6 t+8 \\ e^t & 0 \\ \end{array} \right)$

Muchas de las fórmulas básicas en el cálculo son ciertas en el cálculo matricial. Por ejemplo,

\ begin {ecuación*}\ frac {d (A (t) +B (t))} {d t} =\ frac {d A (t)} {d t} +\ frac {d B (t)} {d t}\ end {ecuación*}

y si$A$ es una matriz constante,

\ comenzar {ecuación*}\ frac {d e^ {A t}} {d t} = A e^ {A t}\ fin {ecuación*}

El cálculo matricial se puede utilizar para resolver sistemas de ecuaciones diferenciales de manera similar al procedimiento utilizado en las ecuaciones diferenciales ordinarias.

Nota SageMath - Matriz Exponencial

El método exponencial matricial de Sage es exp.

view sourceprint?

1	A=Matrix(QQ,[[2,1],[2,3]])

2

A.exp()

Ejercicios

Ejercicio$\PageIndex{1}$

1. Escribe todos los detalles de Ejemplo$\PageIndex{1}$ para mostrar que la fórmula para$F_k$ dada en el texto es correcta.
2. Utilizar la inducción para probar la afirmación hecha en el ejemplo de que$\left( \begin{array}{c} F_k \\ F_{k-1} \\ \end{array} \right)=A^{k-1} \left( \begin{array}{c} 1 \\ 1 \\ \end{array} \right)$

Ejercicio$\PageIndex{2}$

1. Haz el Ejemplo 8.3.7 usando el método descrito en Ejemplo$\PageIndex{1}$. Obsérvese que la ecuación característica terminológica, polinomio característico, y así sucesivamente, introducida en el Capítulo 8, proviene del lenguaje del álgebra matricial,
2. ¿Cuál es la significación del Algoritmo 8.3.1, parte c, con respecto a esta sección?

Ejercicio$\PageIndex{3}$

Resuelve$S(k) = 5S(k - 1) + 4\text{,}$ con el$S(0) = 0\text{,}$ uso del método de esta sección.

Ejercicio$\PageIndex{4}$

¿Cuántos caminos hay de longitud 6 desde el vértice 1 hasta el vértice 3 en la Figura$\PageIndex{2}$? ¿Cuántos caminos del vértice 2 al vértice 2 de longitud 6 hay?

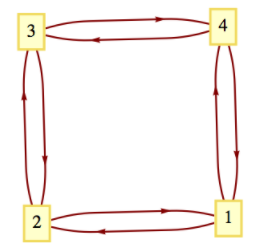Figura$\PageIndex{2}$: Gráfica para el ejercicio$\PageIndex{4}$

Pista

El polinomio característico de la matriz de adyacencia es$\lambda ^4 - 4 \lambda^2\text{.}$

Ejercicio$\PageIndex{5}$

En cuanto al Ejemplo$\PageIndex{2}$,

1. Utilice matrices para determinar el número de caminos de longitud 1 que existen desde el vértice$a$ hasta cada uno de los vértices en la gráfica dada. Verificar usando la gráfica. Haga lo mismo para los vértices$b$ y$c\text{.}$
2. Verifica todos los detalles proporcionados en el ejemplo.
3. Utilice matrices para determinar el número de caminos de longitud 4 ahí entre cada par de nodos en la gráfica. Verifica tus resultados usando la gráfica.

Contestar

1. Dado que$A=A^1= \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ \end{array} \right)\text{,}$ hay 0 rutas de longitud 1 desde: nodo c a nodo a, nodo b a nodo b y nodo a nodo c; y hay 1 ruta de longitud 1 para cada otro par de nodos.
2. El polinomio característico es$\lvert A-c I\rvert = \left| \begin{array}{ccc} 1-c & 1 & 0 \\ 1 & -c & 1 \\ 0 & 1 & 1-c \\ \end{array} \right| = -c^3+2 c^2+c-2$
   Resolviendo la ecuación característica$-c^3+2 c^2+c-2=0$ encontramos soluciones 1, 2 y -1.
   Si$c=1\text{,}$ encontramos el autovector asociado encontrando una solución distinta de cero a$\left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 0 & 1 & 0 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)$ Uno de estos, que será la primera columna de$P\text{,}$ es$\left( \begin{array}{c} 1 \\ 0 \\ -1 \\ \end{array} \right)$
   Si$c=2\text{,}$ el sistema$\left( \begin{array}{ccc} -1 & 1 & 0 \\ 1 & -2 & 1 \\ 0 & 1 & -1 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)$ produce vectores propios, incluyendo los$\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right)\text{,}$ que serán la segunda columna de$P\text{.}$
   Si$c = -1\text{,}$ entonces el sistema que determina los vectores propios es$\left( \begin{array}{ccc} 2 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)$ y podemos seleccionar$\left( \begin{array}{c} 1 \\ -2 \\ 1 \\ \end{array} \right)\text{,}$ aunque cualquier múltiplo distinto de cero de este vector podría ser la tercera columna de$P\text{.}$
3. Ensamblando los resultados de la parte (b) que tenemos$P=\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & -2 \\ -1 & 1 & 1 \\ \end{array} \right)$.
   \ begin {ecuation*}\ begin {split} A^4 & = P\ left (\ begin {array} {ccc} 1^4 & 0 & 0\\ 0 & 2^4 & 0\\ 0 & 0 & (-1) ^ {4}\\ end {array}\\ derecha) P^ {-1} = P\ left (\ begin {array} {ccc} 1 & 0 & 0\ 0 & 16 & 0\\ 0 & 0 & 1\\\ end {array}\ derecha) P^ {-1 }\\ &=\ left (\ begin {array} {ccc} 1 & 16 & 1\\ 0 & 16 & -2\\ -1 & 16 & 1\\ end {array}\\ end {array}\ derecha)\ left (\ begin {array} {ccc}\ frac {1} {2} & 0 & -\ frac {1} {2}\\ frac {1} {3} &\ frac {1} {3} &\ frac {1} {3}\\ frac {1} {6} & -\ frac {1} {3} &\ frac {1} {6}\\ end {array}\ derecha)\ \ &=\ left (\ begin {array} {ccc} 6 & 5 & 5\\ 5 & 6 & 5\\ 5 & 5 & 5 & 6\\\ end {array}\ right)\\ end {split}\ end {equation*}
   De ahí que hay cinco caminos diferentes de longitud 4 entre vértices distintos, y seis caminos diferentes que comienzan y terminan en el mismo vértice. El lector puede verificar estos hechos desde la Figura$\PageIndex{1}$

Ejercicio$\PageIndex{6}$

Let$A =\left( \begin{array}{cc} 2 & -1 \\ -1 & 2 \\ \end{array} \right)$

1. Encuentra$e^A$
2. Recuérdalo$\sin x = \sum _{k=0}^{\infty } \frac{(-1)^k x^k}{(2 k+1)!}$ y computa$\sin A\text{.}$
3. Formular una definición razonable del logaritmo natural de una matriz y calcular$\ln A\text{.}$

Ejercicio$\PageIndex{7}$

Señalamos en el Capítulo 5 que dado que el álgebra matricial no es conmutativo bajo multiplicación, surgen ciertas dificultades. Let$A=\left( \begin{array}{cc} 1 & 1 \\ 0 & 0 \\ \end{array} \right)$ y$B=\left( \begin{array}{cc} 0 & 0 \\ 0 & 2 \\ \end{array} \right)\text{.}$

1. Calcular$e^A\text{,}$$e^B\text{,}$ y$e^{A+B}\text{.}$ Comparar$e^A e^{B}\text{,}$$e^B e^A$ y$e^{A+B}$.
2. Mostrar que si$\pmb{0}$ es la matriz$2\times 2$ cero, entonces$e^{\pmb{0}}= I\text{.}$
3. Demostrar que si$A$ y$B$ son dos matrices que sí conmutan, entonces demostrando$e^{A+B}=e^Ae^B\text{,}$ con ello eso$e^A$ y$e^B$ conmutar.
4. Demuéstralo para cualquier matriz$A\text{,}$$\left(e^A\right)^{-1}= e^{-A}\text{.}$

Contestar

1. $e^A=\left( \begin{array}{cc} e & e \\ 0 & 0 \\ \end{array} \right)$,$e^B=\left( \begin{array}{cc} 0 & 0 \\ 0 & e^2 \\ \end{array} \right)\text{,}$ y$e^{A+B}=\left( \begin{array}{cc} e & e^2-e \\ 0 & e^2 \\ \end{array} \right)$
2. Dejar$\pmb{0}$ ser la matriz cero,$e^{\pmb{0}}=I + \pmb{0}+\frac{\pmb{0}^2}{2}+\frac{\pmb{0}^3}{6}+\ldots =I$.
3. Asumir eso$A$ y$B$ conmutar. Examinaremos los primeros términos en el producto$e^A e^B\text{.}$ El patrón que se establece sí continúa en general. En lo que sigue, es importante que$A B = B A\text{.}$ Por ejemplo, en el último paso,$(A+B)^2$ se expanda a$A^2+A B + B A + B^2\text{,}$ no$A^2+ 2 A B + B^2\text{,}$ si no podemos asumir la conmutatividad.
   \ begin {equation*}\ begin {split} e^ae^b &=\ left (\ sum _ {k=0} ^ {\ infty}\ frac {a^k} {k!} \ derecha)\ izquierda (\ suma _ {k=0} ^ {\ infty}\ frac {b^k} {k!} \ derecha)\\ & =\ izquierda (I + A+\ frac {A^2} {2} +\ frac {A^3} {6} +\ cdots\ derecha)\ izquierda (I +B+\ frac {B^2} {2} +\ frac {B^3} {6} +\ cdots\ derecha)\\ &= I + A + B+\ frac {A^2} {2} + A B +\ frac {B^2} {2} +\ frac {A^3} {6} +\ frac {A^2B} {2} +\ frac {A B^2} {2} +\ frac {B^3} {6} +\ cdots\\ &= I + (A+B) +\ frac {1} {2}}\ izquierda (A^2+ 2 A B + B^2\ derecha) +\ frac {1} {6}\ izquierda (A^3+ 3A^2B+ 3A B^2+ B^3\ derecha) +\ cdots\\ &=I + (A+B) +\ frac {1} {2} (A+B) ^2+\ frac {1} {6} (A+B) ^3+\ cdots\\ & =e^ {A+B}\\ final dividir}\ end {ecuación*}
4. Desde$A$ y$-A$ conmutar, podemos aplicar la parte d;
   \ begin {equation*} e^ae^ {-A} = e^ {A+ (-A)} =e^ {\ pmb {0}} =I\ end {ecuación*}

Ejercicio$\PageIndex{8}$

Otra observación para matrices de adyacencia: Para la matriz en Ejemplo$\PageIndex{2}$, tenga en cuenta que la suma de los elementos en la fila correspondiente al nodo$a$ (es decir, la primera fila) da el outdegree de$a\text{.}$ Similarmente, la suma de los elementos en cualquier columna dada da el indegree del nodo correspondiente a esa columna.

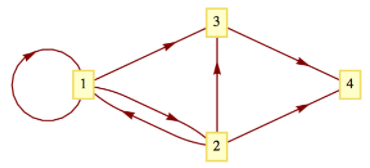Figura$\PageIndex{3}$: Gráfica para el ejercicio$\PageIndex{8}$

1. Usando la matriz$A$ de Ejemplo$\PageIndex{2}$, encuentra el outdegree y el indegree de cada nodo. Verificar por la gráfica.
2. Repita la parte (a) para las gráficas dirigidas en la Figura$\PageIndex{3}$.