9.1: Puntos Ordinarios
- Page ID
- 119123
Si\(x_{0}\) es un punto ordinario de\(Equation \ref{9.1}\), entonces es posible determinar dos series de potencia (es decir, serie Taylor) soluciones para\(y=y(x)\) centrado en\(x=x_{0}\). Ilustramos el método de solución resolviendo dos ejemplos, con\(x_{0}=0\).
Ejemplo: Encuentra la solución general de\(y^{\prime \prime}+y=0\).
A estas alturas, ya debes saber que la solución general es\(y(x)=a_{0} \cos x+a_{1} \sin x\), con\(a_{0}\) y\(a_{1}\) constantes. Para encontrar una solución Power Series sobre el punto\(x_{0}=0\), escribimos
\[y(x)=\sum_{n=0}^{\infty} a_{n} x^{n} \nonumber \]
y al diferenciar término por término
\[y^{\prime}(x)=\sum_{n=1}^{\infty} n a_{n} x^{n-1}, \nonumber \]
y
\[y^{\prime \prime}(x)=\sum_{n=2}^{\infty} n(n-1) a_{n} x^{n-2} \nonumber \]
Sustituyendo la serie de\(y\) potencias y sus derivadas en la ecuación diferencial a resolver, obtenemos
\[\sum_{n=2}^{\infty} n(n-1) a_{n} x^{n-2}+\sum_{n=0}^{\infty} a_{n} x^{n}=0 \nonumber \]
El método de solución de la serie de potencia requiere combinar las dos sumas en el lado izquierdo de la ecuación\ ref {9.2} en una sola serie de potencia en\(x\). Para desplazar el exponente de\(x^{n-2}\) en la primera suma hacia arriba en dos para obtener\(x^{n}\), necesitamos desplazar el índice de suma hacia abajo en dos; es decir,
\[\sum_{n=2}^{\infty} n(n-1) a_{n} x^{n-2}=\sum_{n=0}^{\infty}(n+2)(n+1) a_{n+2} x^{n} . \nonumber \]
Entonces podemos combinar las dos sumas en la Ecuación\ ref {9.2} para obtener
\[\sum_{n=0}^{\infty}\left((n+2)(n+1) a_{n+2}+a_{n}\right) x^{n}=0 . \nonumber \]
Para que la Ecuación\ ref {9.3} sea satisfecha, el coeficiente de cada potencia de\(x\) debe desvanecerse por separado. (Esto se puede probar fijando\(x=0\) después de la diferenciación sucesiva). Por lo tanto, obtenemos la relación de recurrencia
\[a_{n+2}=-\frac{a_{n}}{(n+2)(n+1)}, \quad n=0,1,2, \ldots \nonumber \]
Observamos que los coeficientes pares e impares se desacoplan. Se obtienen así dos secuencias independientes comenzando con el primer término\(a_{0}\) o\(a_{1}\). Desarrollando estas secuencias, tenemos para la secuencia que comienza con\(a_{0}\):
\[\begin{aligned} &a_{0} \\ &a_{2}=-\frac{1}{2} a_{0} \\ &a_{4}=-\frac{1}{4 \cdot 3} a_{2}=\frac{1}{4 \cdot 3 \cdot 2} a_{0} \\ &a_{6}=-\frac{1}{6 \cdot 5} a_{4}=-\frac{1}{6 !} a_{0} \end{aligned} \nonumber \]
y el coeficiente general en esta secuencia para\(n=0,1,2, \ldots\) es
\[a_{2 n}=\frac{(-1)^{n}}{(2 n) !} a_{0} . \nonumber \]
Además, para la secuencia que comienza con\(a_{1}\):
\[\begin{aligned} &a_{1} \\ &a_{3}=-\frac{1}{3 \cdot 2} a_{1} \\ &a_{5}=-\frac{1}{5 \cdot 4} a_{3}=\frac{1}{5 \cdot 4 \cdot 3 \cdot 2} a_{1}, \\ &a_{7}=-\frac{1}{7 \cdot 6} a_{5}=-\frac{1}{7 !} a_{1} \end{aligned} \nonumber \]
y el coeficiente general en esta secuencia para\(n=0,1,2, \ldots\) es
\[a_{2 n+1}=\frac{(-1)^{n}}{(2 n+1) !} a_{1} . \nonumber \]
Utilizando el principio de superposición, la solución general es, por lo tanto
\[\begin{aligned} y(x) &=a_{0} \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n) !} x^{2 n}+a_{1} \sum_{n=0}^{\infty} \frac{(-1)^{n}}{(2 n+1) !} x^{2 n+1} \\ &=a_{0}\left(1-\frac{x^{2}}{2 !}+\frac{x^{4}}{4 !}-\ldots\right)+a_{1}\left(x-\frac{x^{3}}{3 !}+\frac{x^{5}}{5 !}-\ldots\right) \\ &=a_{0} \cos x+a_{1} \sin x \end{aligned} \nonumber \]
como se esperaba.
En nuestro siguiente ejemplo, resolveremos la Ecuación de Airy. Esta ecuación diferencial surge en el estudio de la óptica, la mecánica de fluidos y la mecánica cuántica.
Ejemplo: Encuentra la solución general de\(y^{\prime \prime}-x y=0\).
Con
\[y(x)=\sum_{n=0}^{\infty} a_{n} x^{n} \nonumber \]
la ecuación diferencial se convierte
\[\sum_{n=2}^{\infty} n(n-1) a_{n} x^{n-2}-\sum_{n=0}^{\infty} a_{n} x^{n+1}=0 \nonumber \]
Desplazamos la primera suma a\(x^{n+1}\) desplazando el exponente hacia arriba en tres, es decir,
\[\sum_{n=2}^{\infty} n(n-1) a_{n} x^{n-2}=\sum_{n=-1}^{\infty}(n+3)(n+2) a_{n+3} x^{n+1} \nonumber \]
Al combinar las dos sumas en la Ecuación\ ref {9.4}, separamos el\(n=-1\) término extra en la primera suma dada por\(2 a_{2}\). Por lo tanto,\(Equation \ref{9.4}\) se convierte
\[2 a_{2}+\sum_{n=0}^{\infty}\left((n+3)(n+2) a_{n+3}-a_{n}\right) x^{n+1}=0 . \nonumber \]
Estableciendo coeficientes de potencias de\(x\) a cero, primero encontramos\(a_{2}=0\), y luego obtenemos la relación de recursión
\[a_{n+3}=\frac{1}{(n+3)(n+2)} a_{n} \nonumber \]
Tres secuencias de coeficientes-los que comienzan con uno\(a_{0}, a_{1}\) o\(a_{2}\) -desacople. En particular, las tres secuencias son
\[\begin{aligned} &a_{0}, a_{3}, a_{6}, a_{9}, \ldots \\ &a_{1}, a_{4}, a_{7}, a_{10}, \ldots \\ &a_{2}, a_{5}, a_{8}, a_{11} \ldots \end{aligned} \nonumber \]
Ya que\(a_{2}=0\), encontramos inmediatamente para la última secuencia
\[a_{2}=a_{5}=a_{8}=a_{11}=\cdots=0 . \nonumber \]
Calculamos los primeros cuatro términos distintos de cero en la serie de potencias con coeficientes correspondientes a las dos primeras secuencias. Empezando con\(a_{0}\), tenemos
\[\begin{aligned} &a_{0} \\ &a_{3}=\frac{1}{3 \cdot 2} a_{0} \\ &a_{6}=\frac{1}{6 \cdot 5 \cdot 3 \cdot 2} a_{0} \\ &a_{9}=\frac{1}{9 \cdot 8 \cdot 6 \cdot 5 \cdot 3 \cdot 2} a_{0} \end{aligned} \nonumber \]
y comenzando con\(a_{1}\),
\[\begin{aligned} a_{1} \\ a_{4} &=\frac{1}{4 \cdot 3} a_{1} \\ a_{7} &=\frac{1}{7 \cdot 6 \cdot 4 \cdot 3} a_{1} \\ a_{10} &=\frac{1}{10 \cdot 9 \cdot 7 \cdot 6 \cdot 4 \cdot 3} a_{1} \end{aligned} \nonumber \]
La solución general para\(y=y(x)\), por lo tanto, puede escribirse como
\[\begin{aligned} y(x) &=a_{0}\left(1+\frac{x^{3}}{6}+\frac{x^{6}}{180}+\frac{x^{9}}{12960}+\ldots\right)+a_{1}\left(x+\frac{x^{4}}{12}+\frac{x^{7}}{504}+\frac{x^{10}}{45360}+\ldots\right) \\ &=a_{0} y_{0}(x)+a_{1} y_{1}(x) \end{aligned} \nonumber \]
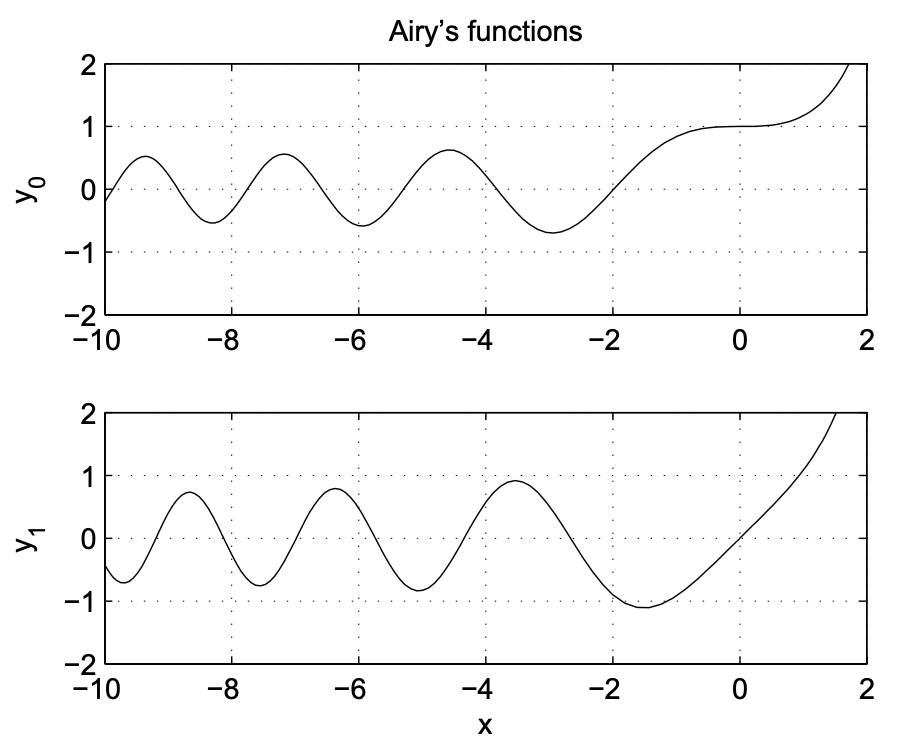
Supongamos que nos gustaría graficar las soluciones\(y=y_{0}(x)\) y\(y=y_{1}(x)\) versus\(x\) resolviendo la ecuación diferencial\(y^{\prime \prime}-x y=0\) numéricamente. ¿Qué condiciones iniciales debemos usar? Claramente,\(y=y_{0}(x)\) resuelve la oda con valores iniciales\(y(0)=1\) y\(y^{\prime}(0)=0\), mientras\(y=y_{1}(x)\) resuelve la oda con valores iniciales\(y(0)=0\) y\(y^{\prime}(0)=1\).
Las soluciones numéricas, obtenidas con MATLAB, se muestran en la Fig. 9.1. Tenga en cuenta que las soluciones oscilan para negativo\(x\) y crecen exponencialmente para positivo\(x\). Esto se puede entender recordando que\(y^{\prime \prime}+y=0\) tiene soluciones oscilatorias de seno y coseno y\(y^{\prime \prime}-y=0\) tiene soluciones de seno y coseno hiperbólico exponencial.