9.4: Serie de coseno y coseno de Fourier
- Page ID
- 116983
La serie de Fourier simplifica si\(f(x)\) es una función par tal que\(f(−x) = f(x)\), o una función impar tal que\(f(−x) = −f(x)\). Se harán uso de los siguientes hechos. La función\(\cos (n\pi x/L)\) es una función par y\(\sin (n\pi x/L)\) es una función impar. El producto de dos funciones pares es una función par. El producto de dos funciones impares es una función par. El producto de una función par e impar es una función impar. Y si\(g(x)\) es una función par, entonces\[\int_{-L}^Lg(x)dx=2\int_0^Lg(x)dx;\nonumber\] y si\(g(x)\) es una función impar, entonces\[\int_{-L}^Lg(x)dx=0.\nonumber\]
Examinamos a su vez la serie de Fourier para una función par o impar. Primero, si\(f(x)\) es par, luego de (9.3.5) y (9.3.6) y nuestros hechos sobre funciones pares e impares, \[\begin{align}a_n&=\frac{2}{L}\int_0^L f(x)\cos\frac{n\pi x}{L}dx,\label{eq:1} \\ b_n&=0.\nonumber\end{align}\]
La serie de Fourier para una función par con periodo\(2L\) viene dada por la serie coseno de Fourier \[\label{eq:2}f(x)=\frac{a_0}{2}+\sum\limits_{n=1}^\infty a_n\cos\frac{n\pi x}{L},\quad f(x)\text{ even}.\]
Segundo, si\(f(x)\) es impar, entonces \[\begin{align} a_n&=0,\nonumber \\ b_n&=\frac{2}{L}\int_0^L f(x)\sin\frac{n\pi x}{L}dx;\label{eq:3}\end{align}\]y la serie de Fourier para una función impar con punto\(2L\) viene dada por la serie sinusoidal de Fourier \[\label{eq:4}f(x)=\sum\limits_{n=1}^\infty b_n\sin\frac{n\pi x}{L},\quad f(x)\text{ odd.}\]
Se pueden obtener ejemplos de series de Fourier calculadas numéricamente usando el applet Java que se encuentra en http://www.falstad.com/fourier. Aquí, demostramos un ejemplo analítico.
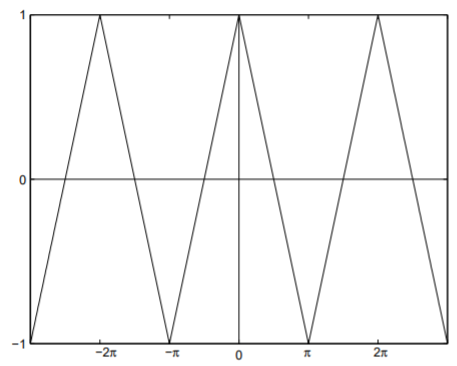
Determinar la serie de coseno de Fourier de la función de triángulo par representada por la Fig. \(\PageIndex{1}\).
Solución
La función de triángulo representada en la Fig. \(\PageIndex{1}\)es una función par de\(x\) con periodo\(2\pi\) (i.e.,\(L =\pi\)). Su definición sobre\(0 < x <\pi\) está dada por\[f(x)=1-\frac{2x}{\pi}.\nonumber\]
Porque\(f(x)\) es par, puede ser representado por la serie coseno de Fourier dada por\(\eqref{eq:1}\) y\(\eqref{eq:2}\). El coeficiente\(a_0\) es\[\begin{aligned}a_0&=\frac{2}{\pi}\int_0^\pi f(x)dx \\ &=\frac{2}{\pi}\int_0^{\pi}\left(1-\frac{2x}{\pi}\right)dx \\ &=\frac{2}{\pi}\left[x-\frac{x^2}{\pi}\right]_0^\pi \\ &=0.\end{aligned}\]
Obsérvese que\(a_0/2\) es el valor promedio de\(f(x)\) más de un periodo, y es obvio a partir de la Fig. \(\PageIndex{1}\)que este valor es cero. Los coeficientes para\(n > 0\) son\[\begin{aligned}a_n&=\frac{2}{\pi}\int_0^\pi f(x)\cos (nx)dx \\ &=\frac{2}{\pi}\int_0^\pi \left(1-\frac{2x}{\pi}\right)\cos (nx)dx \\ &=\frac{2}{\pi}\int_0^\pi \cos (nx)dx-\frac{4}{\pi^2}\int_0^\pi x\cos (nx)dx \\ &=\frac{2}{n\pi}\sin (nx)]_0^\pi -\frac{4}{\pi^2}\left\{\left[\frac{x}{n}\sin (nx)\right]_0^\pi -\frac{1}{n}\int_0^\pi \sin (nx)dx\right\} \\ &=\frac{4}{n\pi^2}\int_0^\pi \sin (nx)dx \\ &=-\frac{4}{n^2\pi^2}\cos (nx)]_0^\pi \\ &=\frac{4}{n^2\pi ^2}(1-\cos (n\pi )).\end{aligned}\]
Ya\[\cos (n\pi )=\left\{\begin{array}{rl}-1,& \text{if }n\text{ odd;} \\ 1,&\text{if }n\text{ even;}\end{array}\right.\nonumber\] que tenemos\[a_n=\left\{\begin{array}{rl}8/(n^2\pi^2),&\text{if }n\text{ odd;} \\ 0,&\text{if }n\text{ even.}\end{array}\right.\nonumber\]
Por lo tanto, la serie de coseno de Fourier para la función triangular viene dada por\[f(x)=\frac{8}{\pi^2}\left(\cos x+\frac{\cos 3x}{3^2}+\frac{\cos 5x}{5^2}+\cdots\right).\nonumber\]
La convergencia de esta serie es rápida. Como un interesante aparte, la evaluación de esta serie en\(x = 0\), usando\(f(0) = 1\), arroja una serie infinita para\(\pi^2/8\):\[\frac{\pi^2}{8}=1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots\nonumber\]
Con la serie de Fourier ahora incluida en nuestra caja de herramientas de matemáticas aplicadas, estamos listos para resolver las ecuaciones de difusión y onda en dominios delimitados.


