4.10: Problema de Dirichlet en el Círculo y el Núcleo de Poisson

Laplace en Coordenadas Polares

Un escenario más natural para la ecuación de Laplace\( \Delta u=0\) es el círculo en lugar del cuadrado. Por otro lado, lo que dificulta un poco el problema es que necesitamos coordenadas polares.

Figura\(\PageIndex{1}\)

Recordemos que las coordenadas polares para el\((x,y)\) plano -son\((r, \theta )\):

\[ x= r \cos \theta, ~~~~ y= r \sin \theta, \nonumber \]

dónde\(r \geq 0\) y\(- \pi < \theta < \pi\). Así\((x,y)\) es la distancia\(r\) desde el origen en ángulo\( \theta\) desde el\(x\) eje positivo.

Figura\(\PageIndex{2}\)

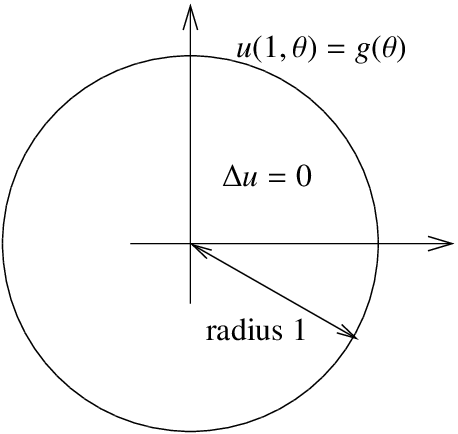
Ahora que conocemos nuestras coordenadas, demos el problema que deseamos resolver. Tenemos una región circular de radio 1, y nos interesa el problema de Dirichlet para la ecuación de Laplace para esta región. Dejar\(u(r, \theta )\) denotar la temperatura en el punto\((r, \theta )\) en coordenadas polares. Tenemos el problema:

\[ \begin{align} \Delta u &=0, & {\rm{for~}} r<1, \label{eq:2} \\ u(1, \theta ) &=g( \theta), &{\rm{for~}} \pi < \theta \leq \pi . \end{align} \nonumber \]

El primer tema al que nos enfrentamos es que no sabemos qué es el laplaciano en coordenadas polares. Normalmente encontraríamos\(u_{xx}\) y\(u_{yy}\) en cuanto a los derivados en\(r\) y\(\theta\). Tendríamos que resolver para\(r\) y\(\theta\) en términos de\(x\) y\(y\). Si bien esto es ciertamente posible, resulta ser más conveniente trabajar a la inversa. En cambio, computemos derivados en\(r\) y\(\theta\) en términos de derivados en\(x\)\(y\) y luego resolvamos. Los cálculos son más fáciles de esta manera. Primero

\[\begin{align}\begin{aligned} x_r &= \cos \theta, &x_{\theta}= -r \sin \theta, \\ y_{r} &= \sin \theta, & y_{\theta}= r \cos \theta . \end{aligned}\end{align} \nonumber \]

Siguiente por regla de cadena obtenemos

\[\begin{align}\begin{aligned} u_r &=u_xx_{r}+u_yy_{r}= \cos(\theta)u_x + \sin(\theta)u_y, \\ u_{rr} &= \cos(\theta)(u_{xx}x_r+u_{xy}y_r)+ \sin(\theta)(u_{yx}x_r+u_{yy}y_r) \\ &= \cos^2(\theta)u_{xx}+2 \cos(\theta) \sin(\theta)u_{xy}+ \sin^2(\theta)u_{yy}.\end{aligned}\end{align} \nonumber \]

De manera similar para la\(\theta\) derivada. Tenga en cuenta que tenemos que usar la regla del producto para la segunda derivada.

\[\begin{align}\begin{aligned} u_{\theta} &=u_xx_{\theta}+u_yy_{\theta}= -r \sin(\theta)u_x + r \cos(\theta)u_y, \\ u_{\theta \theta} &= -r \cos(\theta)(u_x)- r \sin(\theta)(u_{xx}x_{\theta}+u_{xy}y_{\theta})-r \sin(\theta)(u_y)+r \cos(\theta)(u_{yx}x_{\theta}+u_{yy}y_{\theta}) \\ &= -r \cos(\theta)u_{x}-r \sin(\theta)u_y+r^2 \sin^2(\theta)u_{xx}-r^2 2 \sin(\theta) \cos(\theta) u_{xy}+r^2 \cos^2(\theta)u_{yy}.\end{aligned}\end{align} \nonumber \]

Tratemos ahora de resolver para\(u_{xx}+u_{yy}\). Empezamos por\( \frac{1}{r^2}u_{\theta \theta}\) deshacernos de esos molestos\(r^2\). Si agregamos\(u_{rr}\) y usamos el hecho de que\(\cos^2(\theta)+ \sin^2(\theta)=1\), obtenemos

\[ \frac{1}{r^2}u_{\theta \theta} +u_{rr}=u_{xx}+u_{yy}- \frac{1}{r} \cos(\theta)u_x- \frac{1}{r} \sin(\theta)u_y. \nonumber \]

Todavía no estamos del todo, pero todo lo que nos falta es\( \frac{1}{r}u_r\). Agregándolo obtenemos el Laplaciano en coordenadas polares:

\[ \frac{1}{r^2}u_{\theta \theta}+ \frac{1}{r}u_{r}+u_{rr}=u_{xx}+u_{yy}= \Delta u. \nonumber \]

Observe que el laplaciano en coordenadas polares ya no tiene coeficientes constantes.

Solución de la serie

Separemos las variables como de costumbre. Eso es, intentémoslo\(u(r, \theta)=R(r) \Theta ( \theta)\). Entonces

\[0= \Delta u=\frac{1}{r^2}R \Theta''+ \frac{1}{r}R' \Theta+R'' \Theta . \nonumber \]

Pongamos de un\(R\)\( \Theta\) lado y del otro y concluyamos que ambas partes deben ser constantes.

\[\begin{align}\begin{aligned} \frac{1}{r^2}R \Theta'' &= - \left( \frac{1}{r}R'+R'' \right) \Theta . \\ \frac{ \Theta''}{ \Theta} &= - \frac{rR'+r^2R''}{R} + - \lambda.\end{aligned}\end{align} \nonumber \]

Obtenemos dos ecuaciones:

\[\begin{align}\begin{aligned} \Theta''+\lambda \Theta &=0, \\ r^2R''+rR'- \lambda R &=0.\end{aligned}\end{align} \nonumber \]

Centrémonos primero en\( \Theta\). Sabemos que\(u(r, \theta)\) debe ser\(2 \pi\) -periódico en\( \theta\), es decir,\(u(r, \theta)=u(r, \theta +2 \pi)\). Por lo tanto, la solución a\( \Theta''+\lambda \Theta=0\) debe ser\(2 \pi\) -periódica. Hemos visto tal problema en el Ejemplo 4.1.5. Concluimos que\(\lambda=n^2\) para un entero no negativo\(n=0,1,2,3,...\). La ecuación se convierte\( \Theta''+n^2 \Theta=0\). Cuando\(n=0\) la ecuación es justa\( \Theta''=0\), entonces tenemos la solución general\(A \theta+B\). Como\( \Theta\) es periódico,\(A=0\). Para mayor comodidad escribamos esta solución como

\[\Theta_0=\frac{a_0}{2} \nonumber \]

para alguna constante\(a_0\). Para positivo\(n\), la solución\( \Theta''+n^2 \Theta=0\) es

\[ \Theta_n=a_n \cos(n \theta)+b_n \sin(n \theta), \nonumber \]

para algunas constantes\(a_n\) y\(b_n\).

A continuación, consideramos la ecuación para\(R\),

\[r^2R''+rR'-n^2R=0. \nonumber \]

Esta ecuación ha aparecido en ejercicios anteriores, la resolvimos en el Ejercicio 2.E.2.1.6 y el Ejercicio 2.E.1.7. La idea es probar una solución\(r^s\) y si eso no funciona prueba una solución de la forma\(r^s \ln r\). Cuando\(n=0\) obtenemos

\[R_0=Ar^0+Br^0 \ln r=A+B \ln r, \nonumber \]

y si\(n>0\), conseguimos

\[ R_n=Ar^n+Br^{-n}. \nonumber \]

La función\(u(r, \theta)\) debe ser finita en el origen, es decir, cuándo\(r=0\). Por lo tanto,\(B=0\) en ambos casos. Pongámonos también\(A=1\) en ambos casos, las constantes en\( \Theta_n\) recogerán la holgura para que no perdamos nada. Por lo tanto, vamos

\[ R_0=1,\quad\text{and}\quad R_n=r^n. \nonumber \]

De ahí que nuestras soluciones de bloques de construcción sean

\[u_0(r, \theta)= \frac{a_0}{2},\quad u_n(r, \theta)=a_n r^n \cos(n \theta)+b_n r^n \sin(n \theta). \nonumber \]

Armando todo nuestra solución es:

\[u(r, \theta)= \frac{a_0}{2}+ \sum_{n=1}^{\infty}a_n r^n \cos(n \theta)+b_n r^n \sin(n \theta). \nonumber \]

Nos fijamos en la condición límite en\(\eqref{eq:2}\),

\[g(\theta)=u(1, \theta)= \frac{a_0}{2}+ \sum_{n=1}^{\infty}a_n \cos(n \theta)+b_n \sin(n \theta). \nonumber \]

Por lo tanto, la solución\(\eqref{eq:2}\) es expandirse\(g(\theta)\), que es una función\(2 \pi\) -periódica como una serie de Fourier, y luego la\(n^{\text{th}}\) coordenada se multiplica por\(r^n\). En otras palabras, para calcular\(a^n\) y a\(b^n\) partir de la fórmula podemos, como de costumbre, calcular

\[a_n= \frac{1}{ \pi} \int_{ \pi}^{- \pi} g(\theta) \cos(n \theta)d \theta, \quad\text{and}\quad b_n= \frac{1}{ \pi} \int_{ \pi}^{- \pi} g(\theta) \sin(n \theta)d \theta. \nonumber \]

Ejemplo\(\PageIndex{1}\)

Supongamos que deseamos resolver

\[\begin{align}\begin{aligned} & \Delta u = 0 , \qquad 0 \leq r < 1, \quad -\pi < \theta \leq \pi,\\ & u(1,\theta) = \cos(10\,\theta), \qquad -\pi < \theta \leq \pi.\end{aligned}\end{align} \nonumber \]

La solución es

\[ u(r, \theta)=r^{10} \cos(10 \theta). \nonumber \]

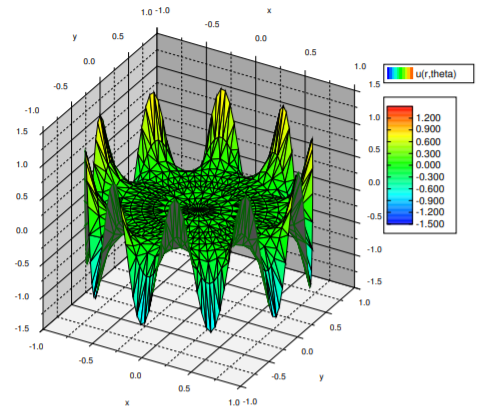
Ver la trama en la Figura\(\PageIndex{3}\). Lo que hay que notar en este ejemplo es que el efecto de una alta frecuencia se siente mayormente en el límite. En medio del disco, la solución está muy cerca de cero. Eso es porque\(r^{10}\) bastante pequeño cuando\(r\) está cerca de\(0\).

Figura\(\PageIndex{3}\): La solución del problema de Dirichlet en el disco con datos\(\cos (10\theta )\) como límite.

Ejemplo\(\PageIndex{2}\)

Resolvamos un problema más difícil. Supongamos que tenemos una varilla larga con sección transversal circular de radio\(1\) y deseamos resolver el problema de calor de estado estacionario. Si la varilla es lo suficientemente larga simplemente necesitamos resolver la ecuación de Laplace en dos dimensiones. Pongamos el centro de la varilla en el origen y tenemos exactamente la región que estamos estudiando actualmente, un círculo de radio\(1\). Para las condiciones de contorno, supongamos en coordenadas cartesianas\(x\) y\(y\), la temperatura se fija en\(0\) cuándo\(y<0\) y en\(2y\) cuándo\(y>0\).

Nosotros configuramos el problema. Como\(y=r \sin(\theta)\), entonces en el círculo de radio\(1\) que tenemos\(2y=2 \sin(\theta)\). Entonces

\[\begin{align}\begin{aligned} & \Delta u = 0 , \qquad 0 \leq r < 1, \quad -\pi < \theta \leq \pi,\\ & u(1,\theta) = \begin{cases} 2\sin(\theta) & \text{if } \; \phantom{-}0 \leq \theta \leq \pi, \\ 0 & \text{if } \; {-\pi} < \theta < 0. \end{cases}\end{aligned}\end{align} \nonumber \]

Ahora debemos calcular la serie de Fourier para la condición de límite. A estas alturas el lector tiene abundante experiencia en la computación de series de Fourier y por eso simplemente declaramos que

\[ u(1, \theta)= \frac{2}{\pi}+ \sin(\theta)+ \sum_{n=1}^{\infty} \frac{-4}{\pi (4n^2-1)} \cos(2n \theta). \nonumber \]

Ejercicio\(\PageIndex{1}\)

Calcular la serie para\(u(1, \theta)\) y verificar que realmente es lo que acabamos de reclamar. Pista: Ten cuidado, asegúrate de no dividir por cero.

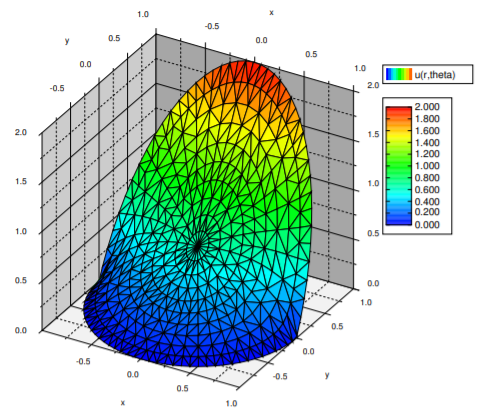
Ahora simplemente escribimos la solución (ver Figura\(\PageIndex{4}\)) multiplicando por\(r^n\) en los lugares correctos.

\[ u(r, \theta)= \frac{2}{\pi}+ r\sin(\theta)+ \sum_{n=1}^{\infty} \frac{-4r^{2n}}{\pi (4n^2-1)} \cos(2n \theta). \nonumber \]

Figura\(\PageIndex{4}\): La solución del problema de Dirichlet con datos de límites\(0\) para\(y<0\) y\(2y\) para\(y>0\).

Núcleo de Poisson

Hay otra manera de resolver el problema de Dirichlet con la ayuda de un kernel integral. Es decir, encontraremos una función\(P(r,\theta,\alpha)\) llamada kernel de Poisson \(^{1}\)tal que

\[u(r,\theta)= \frac{1}{2\pi} \int_{-\pi}^{\pi}P(r,\theta,\alpha)g(\alpha)d\alpha. \nonumber \]

Si bien la integral generalmente no será resoluble analíticamente, se puede evaluar numéricamente. De hecho, a menos que los datos de límite ya se den como una serie de Fourier, será mucho más fácil evaluar numéricamente esta fórmula ya que solo hay una integral que evaluar.

La fórmula también tiene aplicaciones teóricas. Por ejemplo, como\(P(r,\theta,\alpha)\) tendrá infinitamente muchos derivados, entonces a través de la diferenciación bajo la integral encontramos que la solución\(u(r,\theta)\) tiene infinitamente muchos derivados, al menos cuando está dentro del círculo,\(r<1\). Por infinitamente muchos derivados lo que se debe pensar es que “no\(u(r,\theta)\) tiene esquinas” y todas sus derivadas parciales existen también y además “no tienen esquinas”.

Calcularemos la fórmula para\(P(r,\theta,\alpha)\) a partir de la solución en serie, y esta idea se puede aplicar en cualquier momento que tenga una solución de serie conveniente donde los coeficientes se obtengan a través de la integración. De ahí que pueda aplicar este razonamiento para obtener dichos núcleos integrales para otras ecuaciones, como la ecuación de calor. El cálculo es largo y tedioso, pero no demasiado difícil. Dado que las ideas a menudo se aplican en contextos similares, es bueno entender cómo funciona este cálculo.

Lo que hacemos es comenzar con la solución de series y sustituir los coeficientes por las integrales que los computen. Entonces tratamos de escribir todo como una sola integral. Debemos usar una variable ficticio diferente para la integración y por lo tanto usamos\(\alpha\) en lugar de\(\theta\).

\[\begin{align}\begin{aligned} u(r,\theta )&=\frac{a_{0}}{2}+\sum\limits_{n=1}^\infty a_{n}r^{n}\cos (n\theta )+b_{n}r^{n}\sin (n\theta ) \\ &=\underset{\frac{a_{0}}{2}}{\underbrace{\left(\frac{1}{2\pi}\int_{-\pi}^{\pi}g(\alpha )d\alpha\right)}}+\sum\limits_{n=1}^\infty \underset{a_{n}}{\underbrace{\left(\frac{1}{\pi}\int_{-\pi}^{\pi}g(\alpha)\cos (n\alpha )d\alpha\right)}}r^{n}\cos (n\theta) \\ &+\underset{b_{n}}{\underbrace{\left(\frac{1}{\pi}\int_{-\pi}^{\pi}g(\alpha)\sin (n\alpha)d\alpha\right)}}r^{n}\sin (n\theta ) \\ &=\frac{1}{2\pi}\int_{-\pi}^{\pi}\left(g(\alpha)+2\sum\limits_{n=1}^\infty g(\alpha)\cos (n\alpha)r^{n}\cos (n\theta )+g(\alpha )\sin (n\alpha )r^{n}\sin (n\theta )\right) d\alpha \\ &=\frac{1}{2\pi}\int_{-\pi}^{\pi}\underset{P(r,\theta ,\alpha )}{\underbrace{\left( 1+2\sum\limits_{n=1}^\infty r^{n}\left(\cos (n\alpha )\cos (n\theta )+\sin (n\alpha )\sin (n\theta )\right)\right)}}g(\alpha )d\alpha \end{aligned}\end{align} \nonumber \]

OK, entonces tenemos lo que queríamos, la expresión entre paréntesis es el kernel de Poisson,\(P(r,\theta,\alpha)\). No obstante, podemos hacerlo mucho mejor. Todavía se da como una serie, y realmente nos gustaría tener una expresión agradable y simple para ello. Debemos trabajar un poco más duro. El truco es reescribir todo en términos de exponenciales complejos. Trabajemos solo en el kernel.

\[\begin{align}\begin{aligned} P(r,\theta,\alpha) &=1+2\sum_{n=1}^{\infty}r^n(\cos(n\alpha)\cos(n\theta)+ \sin(n\alpha)\sin(n\theta)) \\ &= 1+2\sum_{n=1}^{\infty}r^n \cos(n(\theta- \alpha)) \\ &= 1+2\sum_{n=1}^{\infty}r^n(e^{in(\theta-\alpha)}+e^{-in(\theta-\alpha)}) \\ &= 1+\sum_{n=1}^{\infty}(re^{i(\theta-\alpha)})^n+\sum_{n=1}^{\infty}(re^{-i(\theta-\alpha)})^n.\end{aligned}\end{align} \nonumber \]

En la expresión anterior reconocemos las series geométricas. Es decir, recordar del cálculo que siempre y cuando\( |z|<1\), entonces

\[\sum_{n=1}^{\infty}z^n= \frac{z}{1-z}. \nonumber \]

Tenga en cuenta que\(n\) empieza a las\(1\) y por eso tenemos el\(z\) en el numerador. Es la serie geométrica estándar multiplicada por\(z\). Sigamos con el cómputo.

\[\begin{align}\begin{aligned} P(r,\theta,\alpha) &=1+\sum_{n=1}^{\infty}(re^{i(\theta-\alpha)})^n+\sum_{n=1}^{\infty}(re^{-i(\theta-\alpha)})^n \\ &= 1+ \frac{re^{i(\theta-\alpha)}}{1-re^{i(\theta-\alpha)}}+ \frac{re^{-i(\theta-\alpha)}}{1-re^{-i(\theta-\alpha)}} \\ &=\frac{(1-re^{i(\theta-\alpha)})(1-re^{-i(\theta-\alpha)})+(1-re^{-i(\theta-\alpha)})re^{ i(\theta-\alpha)}+(1-re^{i(\theta-\alpha)})re^{ - i(\theta-\alpha)}}{(1-re^{i(\theta-\alpha)})(1-re^{-i(\theta-\alpha)})} \\ &= \frac{1-r^2}{1-re^{i(\theta-\alpha)}-re^{-i(\theta-\alpha)}+r^2} \\ &= \frac{1-r^2}{1-2r\cos(\theta-\alpha)+r^2}.\end{aligned}\end{align} \nonumber \]

Ahora esa es una fórmula con la que podemos vivir. La solución al problema de Dirichlet usando el kernel de Poisson es

\[u(r, \theta)= \frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1-r^2}{1-2r\cos(\theta-\alpha)+r^2}g(\alpha)d\alpha. \nonumber \]

A veces la fórmula para el kernel de Poisson se da junto con la constante\(\frac{1}{2\pi}\), en cuyo caso por supuesto no debemos dejarlo frente a la integral. También, muchas veces se dan los límites de la integral en cuanto\(0\) a\(2\pi\); todo dentro es\(2\pi\) -periódico en\(\alpha\), por lo que esto no cambia la integral.

No dejemos el núcleo de Poisson sin explicar su significado geométrico. Deja\(s\) ser la distancia de\((r,\theta)\) a\((1,\alpha)\). Se puede recordar del cálculo que esta distancia\(s\) en coordenadas polares viene dada precisamente por la raíz cuadrada de\(1-2r\cos(\theta-\alpha)+r^2\). Es decir, el kernel de Poisson es realmente la fórmula

\[\frac{1-r^2}{s^2}. \nonumber \]

Figura\(\PageIndex{5}\)

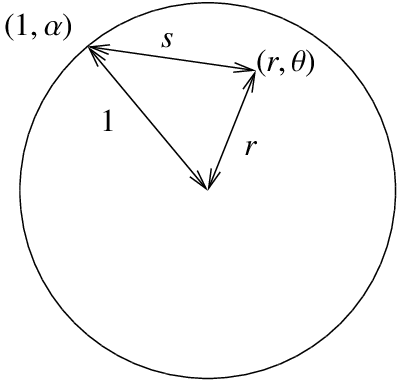
Una nota final que hacemos sobre la fórmula es señalar que realmente es un promedio ponderado de los valores límite. Primero veamos qué sucede en el origen, es entonces cuando\(r=0\).

\[\begin{align}\begin{aligned} u(0,0) &= \frac{1}{2\pi} \int_{-\pi}^{\pi} \frac{1-0^2}{1-2(0)\cos(\theta-\alpha)+0^2}g(\alpha)d\alpha \\ &= \frac{1}{2\pi} \int_{-\pi}^{\pi} g(\alpha)d\alpha. \end{aligned}\end{align} \nonumber \]

Así\(u(0,0)\) es precisamente el valor promedio de\(g(\theta)\) y por lo tanto el valor promedio de\(u\) en el límite. Esta es una característica general de las funciones armónicas, el valor en algún momento\(p\) es igual al promedio de los valores en un círculo centrado en\(p\).

Lo que dice la fórmula es que el valor de la solución en cualquier punto del círculo es un promedio ponderado de los datos de límite\(g(\theta)\). El kernel es más grande cuando\((r,\theta)\) está más cerca de\((1,\alpha)\). Por lo tanto a la hora de calcular le\(u(r,\theta)\) damos más peso a los valores\(g(\alpha)\) cuando\((1,\alpha)\) está más cerca\((r,\theta)\) y menos peso a los valores\(g(\theta)\) cuando está\((1,\alpha)\) lejos de\((r,\theta)\).

Notas al pie

[1] Nombrado así por el matemático francés Sim éon Denis Poisson (1781 — 1840).