8.6: Convolución
- Page ID
- 114837
En esta sección consideramos el problema de encontrar la transformada inversa de Laplace de un producto\(H(s)=F(s)G(s)\), donde\(F\) y\(G\) son las transformaciones de Laplace de funciones conocidas\(f\) y\(g\). Para motivar nuestro interés en este problema, considere el problema de valor inicial
\[ay''+by'+cy=f(t),\quad y(0)=0,\quad y'(0)=0.\nonumber \]
Tomar Laplace transforma los rendimientos
\[(as^2+bs+c)Y(s)=F(s),\nonumber \]
por lo
\[\label{eq:8.6.1} Y(s)=F(s)G(s),\]
donde
\[G(s)={1\over as^2+bs+c}.\nonumber \]
Hasta ahora no nos interesaba la factorización señalada en la Ecuación\ ref {eq:8.6.1}, ya que tratábamos únicamente de ecuaciones diferenciales con funciones de forzamiento específicas. De ahí que simplemente podríamos hacer la multiplicación indicada en la Ecuación\ ref {eq:8.6.1} y usar la tabla de transformaciones de Laplace para encontrar\(y={\cal L}^{-1}(Y)\). Sin embargo, esto no es posible si queremos una fórmula para\(y\) en términos de\(f\), que puede no estar especificada.
Para motivar la fórmula para\({\cal L}^{-1}(FG)\), considerar el problema de valor inicial
\[\label{eq:8.6.2} y'-ay=f(t),\quad y(0)=0,\]
que primero resolvemos sin usar la transformación de Laplace. La solución de la ecuación diferencial en la Ecuación\ ref {eq:8.6.2} es de la forma\(y=ue^{at}\) donde
\[u'=e^{-at}f(t).\nonumber \]
Integrando esto de\(0\) a\(t\) e imponiendo los\(u(0)=y(0)=0\) rendimientos de la condición inicial
\[u=\int_0^t e^{-a\tau}f(\tau)\,d\tau.\nonumber \]
Por lo tanto
\[\label{eq:8.6.3} y(t)=e^{at}\int_0^t e^{-a\tau}f(\tau)\,d\tau=\int_0^t e^{a(t-\tau)}f(\tau)\,d\tau.\]
Ahora usaremos la transformada de Laplace para resolver la Ecuación\ ref {eq:8.6.2} y compararemos el resultado con la Ecuación\ ref {eq:8.6.3}. Tomando Laplace transforma en Ecuación\ ref {eq:8.6.2} rendimientos
\[(s-a)Y(s)=F(s),\nonumber \]
por lo
\[Y(s)=F(s) {1\over s-a},\nonumber \]
lo que implica que
\[\label{eq:8.6.4} y(t)= {\cal L}^{-1}\left(F(s){1\over s-a}\right).\]
Si ahora lo dejamos\(g(t)=e^{at}\), para que
\[G(s)={1\over s-a},\nonumber \]
entonces la Ecuación\ ref {eq:8.6.3} y la Ecuación\ ref {eq:8.6.4} se pueden escribir como
\[y(t)=\int_0^tf(\tau)g(t-\tau)\,d\tau\nonumber \]
y
\[y={\cal L}^{-1}(FG),\nonumber \]
respectivamente. Por lo tanto
\[\label{eq:8.6.5} {\cal L}^{-1}(FG)=\int_0^t f(\tau)g(t-\tau)\,d\tau\]
en este caso.
Esto motiva la siguiente definición.
La convolución\(f*g\) de dos funciones\(f\) y\(g\) se define por
\[(f*g)(t)=\int_0^t f(\tau)g(t-\tau)\,d\tau.\nonumber \]
Se puede demostrar (Ejercicio 8.6.6) que\(f\ast g=g\ast f\); es decir,
\[\int_0^tf(t-\tau)g(\tau)\,d\tau=\int_0^tf(\tau)g(t-\tau)\,d\tau. \nonumber\]
La ecuación\ ref {eq:8.6.5} muestra que\({\cal L}^{-1}(FG)=f*g\) en el caso especial donde\(g(t)=e^{at}\). Este siguiente teorema afirma que esto es cierto en general.
Si\({\cal L}(f)=F\) y\({\cal L}(g)=G,\) entonces
\[{\cal L}(f*g)=FG.\nonumber \]
Una prueba completa del teorema de la convolución está más allá del alcance de este libro. Sin embargo, asumiremos que\(f\ast g\) tiene una transformación de Laplace y verificaremos la conclusión del teorema de una manera puramente computacional. Por la definición de la transformación de Laplace,
\[{\cal L}(f\ast g)=\int_0^\infty e^{-st}(f\ast g)(t)\,dt=\int_0^\infty e^{-st} \int_0^t f(\tau)g(t-\tau)\,d\tau\,dt.\nonumber \]
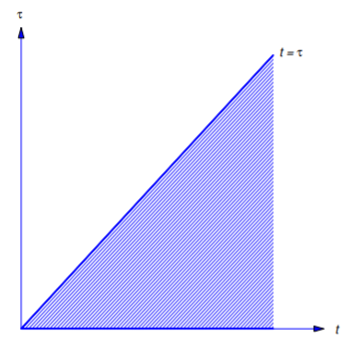
Esta integral iterada equivale a una integral doble sobre la región que se muestra en la Figura 8.6.1 . Invertir el orden de los rendimientos de integración
\[\label{eq:8.6.6} {\cal L}(f*g)=\int_0^\infty f(\tau)\int^\infty_\tau e^{-st}g(t-\tau)\, dt \,d\tau.\]
Sin embargo, la sustitución\(x=t-\tau\) muestra que
\[\begin{align*} \int^\infty_\tau e^{-st}g(t-\tau)\,dt&=\int_0^\infty e^{-s(x+\tau)}g(x)\,dx\\[4pt] &= e^{-s\tau}\int_0^\infty e^{-sx}g(x)\,dx=e^{-s\tau}G(s).\end{align*}\nonumber \]
Sustituyendo esto en la Ecuación\ ref {eq:8.6.6} y señalando que\(G(s)\) es independiente de\(\tau\) los rendimientos
\[\begin{align*} {\cal L}(f\ast g)&= \int_0^\infty e^{-s\tau} f(\tau)G(s)\,d\tau\\[4pt] & =G(s)\int_0^\infty e^{-st}f(\tau)\,d\tau=F(s)G(s).\end{align*}\nonumber \]
Let
\[f(t)=e^{at}\quad \text{and} \quad g(t)=e^{bt}\qquad (a\ne b).\nonumber \]
Verificar eso\({\cal L}(f\ast g)={\cal L}(f){\cal L}(g)\), como lo implica el teorema de la convolución.
Solución
Primero computamos
\[\begin{aligned} (f\ast g) &= \int_{0}^{t}e^{a\tau }e^{b(t-\tau )}d\tau &=e^{bt}\int_{0}^{t}e^{(a-b)\tau }d\tau \\ &= \left. e^{bt}\frac{e^{a-b}\tau }{a-b} \right|_{0}^{t} &=\frac{e^{bt}[e^{(a-b)t}-1] }{a-b} \\ &=\frac{e^{at}-e^{bt}}{a-b} \end{aligned}\nonumber \]
Desde
\[e^{at}\leftrightarrow {1\over s-a}\quad\mbox{ and }\quad e^{bt}\leftrightarrow {1\over s-b},\nonumber \]
se deduce que
\[\begin{aligned} {\cal L}(f\ast g)&={1\over a-b}\left[{1\over s-a}-{1\over s-b}\right]\\[5pt] &={1\over(s-a)(s-b)}\\[5pt] &={\cal L}(e^{at}){\cal L}(e^{bt})={\cal L}(f){\cal L}(g).\end{aligned}\nonumber \]
Una fórmula para la solución de un problema de valor inicial
El teorema de convolución proporciona una fórmula para la solución de un problema de valor inicial para una ecuación de segundo orden de coeficiente constante lineal con una no especificada. Los siguientes tres ejemplos ilustran esto.
Encuentre una fórmula para la solución del problema de valor inicial
\[\label{eq:8.6.7} y''-2y'+y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]
Solución
Tomando Laplace transforma en Ecuación\ ref {eq:8.6.7} rendimientos
\[(s^2-2s+1)Y(s)=F(s)+(k_1+k_0s)-2k_0.\nonumber \]
Por lo tanto
\[\begin{align*} Y(s)&= {1\over(s-1)^2}F(s)+{k_1+k_0s-2k_0\over(s-1)^2}\\[5pt] &= {1\over(s-1)^2}F(s)+{k_0\over s-1}+{k_1-k_0\over(s-1)^2}.\end{align*}\nonumber \]
De la mesa de Laplace transforma,
\[{\cal L}^{-1}\left({k_0\over s-1}+{k_1-k_0\over(s-1)^2}\right) =e^t\left(k_0+(k_1-k_0)t\right). \nonumber\]
Desde
\[{1\over(s-1)^2}\leftrightarrow te^t\quad \text{and} \quad F(s) \leftrightarrow f(t), \nonumber\]
el teorema de convolución implica que
\[{\cal L}^{-1} \left({1\over(s-1)^2}F(s)\right)= \int_0^t\tau e^\tau f(t-\tau)\,d\tau. \nonumber\]
Por lo tanto, la solución de la Ecuación\ ref {eq:8.6.7} es
\[y(t)=e^t\left(k_0+(k_1-k_0)t\right)+\int_0^t\tau e^\tau f(t-\tau)\, d\tau. \nonumber\]
Encuentre una fórmula para la solución del problema de valor inicial
\[\label{eq:8.6.8} y''+4y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]
Solución
Tomando Laplace transforma en Ecuación\ ref {eq:8.6.8} rendimientos
\[(s^2+4)Y(s) =F(s)+k_1+k_0s. \nonumber\]
Por lo tanto
\[Y(s) ={1\over(s^2+4)}F(s)+{k_1+k_0s\over s^2+4}. \nonumber\]
De la mesa de Laplace transforma,
\[{\cal L}^{-1}\left(k_1+k_0s\over s^2+4\right)=k_0\cos 2t+{k_1\over 2}\sin 2t. \nonumber\]
Desde
\[{1\over(s^2+4)}\leftrightarrow {1\over 2}\sin 2t\quad \text{and} \quad F(s)\leftrightarrow f(t), \nonumber\]
el teorema de convolución implica que
\[{\cal L}^{-1}\left({1\over(s^2+4)}F(s)\right)= {1\over 2}\int_0^t f(t-\tau)\sin 2\tau\, d\tau. \nonumber \]
Por lo tanto, la solución de la Ecuación\ ref {eq:8.6.8} es
\[y(t)=k_0\cos 2t+{k_1\over 2}\sin 2t+{1\over 2}\int_0^tf(t-\tau)\sin 2\tau\,d\tau. \nonumber\]
Encuentre una fórmula para la solución del problema de valor inicial
\[\label{eq:8.6.9} y''+2y'+2y=f(t),\quad y(0)=k_0,\quad y'(0)=k_1.\]
Solución
Tomando Laplace transforma en Ecuación\ ref {eq:8.6.9} rendimientos
\[(s^2+2s+2)Y(s)=F(s)+k_1+k_0s+2k_0.\nonumber \]
Por lo tanto
\[\begin{aligned} Y(s)&=\frac{1}{(s+1)^{2}+1}F(s)+\frac{k_{1}+k_{0}s+2k_{0}}{(s+1)^{2}+1} \\ &=\frac{1}{(s+1)^{2}+1}F(s)+\frac{(k_{1}+k_{0})+k_{0}(s+1)}{(s+1)^{2}+1} \end{aligned} \nonumber \]
De la mesa de Laplace transforma,
\[{\cal L}^{-1}\left((k_1+k_0)+k_0(s+1)\over(s+1)^2+1\right)= e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right). \nonumber\]
Desde
\[{1\over(s+1)^2+1}\leftrightarrow e^{-t}\sin t \quad \text{and} \quad F(s)\leftrightarrow f(t), \nonumber\]
el teorema de convolución implica que
\[{\cal L}^{-1}\left({1\over(s+1)^2+1}F(s)\right)= \int_0^t f(t-\tau)e^{-\tau}\sin\tau \,d\tau. \nonumber\]
Por lo tanto, la solución de la Ecuación\ ref {eq:8.6.9} es
\[\label{eq:8.6.10} y(t)=e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right)+\int_0^tf(t-\tau)e^{-\tau}\sin\tau\,d\tau.\]
Evaluación de Integrales de Convolución
Diremos que una integral de la forma\(\int_0^t u(\tau)v(t-\tau)\,d\tau\) es una integral de convolución. El teorema de convolución proporciona una manera conveniente de evaluar integrales de convolución.
Evaluar la integral de convolución
\[h(t)=\int_0^t(t-\tau)^5\tau^7 d\tau. \nonumber\]
Solución
Podríamos evaluar esta integral expandiéndonos\((t-\tau)^5\) en poderes de\(\tau\) y luego integrándonos. Sin embargo, el teorema de convolución proporciona una manera más fácil. La integral es la convolución de\(f(t)=t^5\) y\(g(t)=t^7\). Desde
\[t^5\leftrightarrow {5!\over s^6}\quad\mbox{ and }\quad t^7 \leftrightarrow {7!\over s^8},\nonumber \]
el teorema de convolución implica que
\[h(t)\leftrightarrow {5!7!\over s^{14}}={5!7!\over 13!}\, {13! \over s^{14}},\nonumber \]
donde hemos escrito la segunda igualdad porque
\[{13!\over s^{14}}\leftrightarrow t^{13}.\nonumber \]
Por lo tanto,
\[h(t)={5!7!\over 13!}\, t^{13}.\nonumber \]
Utilizar el teorema de convolución y una expansión parcial de la fracción para evaluar la integral de convolución
\[h(t)=\int_0^t\sin a(t-\tau)\cos b\tau\,d\tau\quad (|a|\ne |b|).\nonumber \]
Solución
Desde
\[\sin at\leftrightarrow {a\over s^2+a^2}\quad\mbox{and}\quad \cos bt\leftrightarrow {s\over s^2+b^2},\nonumber \]
el teorema de convolución implica que
\[H(s)={a\over s^2+a^2}{s\over s^2+b^2}.\nonumber \]
Ampliar esto en una fracción parcial de expansión de rendimientos
\[H(s)={a\over b^2-a^2}\left[{s\over s^2+a^2}-{s\over s^2+b^2}\right].\nonumber \]
Por lo tanto
\[h(t)={a\over b^2-a^2}\left(\cos at-\cos bt\right).\nonumber \]
Ecuaciones Integrales de Volterra
Una ecuación de la forma
\[\label{eq:8.6.11} y(t)=f(t)+\int_0^t k(t-\tau) y(\tau)\,d\tau\]
es una ecuación integral de Volterra. Aquí\(f\) y\(k\) se les dan funciones y\(y\) se desconoce. Dado que la integral de la derecha es una integral de convolución, el teorema de convolución proporciona una fórmula conveniente para resolver la Ecuación\ ref {eq:8.6.11}. Tomando Laplace transforma en Ecuación\ ref {eq:8.6.11} rendimientos
\[Y(s)=F(s)+K(s) Y(s),\nonumber \]
y resolviendo esto para\(Y(s)\) rendimientos
\[Y(s)={F(s)\over 1-K(s)}.\nonumber \]
Luego obtenemos la solución de la Ecuación\ ref {eq:8.6.11} as\(y={\cal L}^{-1}(Y)\).
Resolver la ecuación integral
\[\label{eq:8.6.12} y(t)=1+2\int_0^t e^{-2(t-\tau)} y(\tau)\,d\tau.\]
Solución
Tomando Laplace transforma en Ecuación\ ref {eq:8.6.12} rendimientos
\[Y(s)={1\over s}+{2\over s+2} Y(s),\nonumber \]
y resolviendo esto para\(Y(s)\) rendimientos
\[Y(s)={1\over s}+{2\over s^2}.\nonumber \]
Por lo tanto,
\[y(t)=1+2t.\nonumber \]
Funciones de transferencia
El siguiente teorema presenta una fórmula para la solución del problema general del valor inicial
\[ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\nonumber \]
donde asumimos por simplicidad que\(f\) es continuo\([0,\infty)\) y que\({\cal L}(f)\) existe. En Ejercicios 8.6.11-8.6.14 se demuestra que la fórmula es válida bajo condiciones mucho más débiles sobre\(f\).
Supongamos que\(f\) es continuo\([0,\infty)\) y tiene una transformación de Laplace. Entonces la solución del problema de valor inicial
\[\label{eq:8.6.13} ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\]
es
\[\label{eq:8.6.14} y(t)=k_0y_1(t)+k_1y_2(t)+\int_0^tw(\tau)f(t-\tau)\,d\tau,\]
donde\(y_1\) y\(y_2\) satisfacer
\[\label{eq:8.6.15} ay_1''+by_1'+cy_1=0,\quad y_1(0)=1,\quad y_1'(0)=0,\]
y
\[\label{eq:8.6.16} ay_2''+by_2'+cy_2=0,\quad y_2(0)=0,\quad y_2'(0)=1,\]
y
\[\label{eq:8.6.17} w(t)={1\over a}y_2(t).\]
- Prueba
-
Tomando Laplace transforma en Ecuación\ ref {eq:8.6.13} rendimientos
\[p(s)Y(s)=F(s)+a(k_1+k_0s)+bk_0,\nonumber \]
donde
\[p(s)=as^2+bs+c.\nonumber \]
Por lo tanto,
\[\label{eq:8.6.18} Y(s)=W(s)F(s)+V(s)\]
con
\[\label{eq:8.6.19} W(s)={1\over p(s)}\]
y
\[\label{eq:8.6.20} V(s)={a(k_1+k_0s)+bk_0\over p(s)}.\]
Tomando las transformaciones de Laplace en la Ecuación\ ref {eq:8.6.15} y la Ecuación\ ref {eq:8.6.16} muestra que
\[p(s)Y_1(s)=as+b\quad\mbox{and}\quad p(s)Y_2(s)=a.\nonumber \]
Por lo tanto
\[Y_1(s)={as+b\over p(s)}\nonumber \]
y
\[\label{eq:8.6.21} Y_2(s)={a\over p(s)}.\]
Por lo tanto, la ecuación\ ref {eq:8.6.20} se puede reescribir como
\[V(s)=k_0Y_1(s)+k_1Y_2(s).\nonumber \]
Sustituyendo esto en la ecuación\ ref {eq:8.6.18} rendimientos
\[Y(s)=k_0Y_1(s)+k_1Y_2(s)+{1\over a}Y_2(s)F(s).\nonumber \]
Tomando transformaciones inversas e invocando el teorema de convolución produce la Ecuación\ ref {eq:8.6.14}. Finalmente, la Ecuación\ ref {eq:8.6.19} y la Ecuación\ ref {eq:8.6.21} implican la Ecuación\ ref {eq:8.6.17}.
Es útil anotar de la Ecuación\ ref {eq:8.6.14} que\(y\) es de la forma
\[y=v+h,\nonumber \]
donde
\[v(t)=k_0y_1(t)+k_1y_2(t)\nonumber \]
depende de las condiciones iniciales y es independiente de la función de forzamiento, mientras
\[h(t)=\int_0^tw(\tau)f(t-\tau)\, d\tau\nonumber \]
depende de la función de forzamiento y es independiente de las condiciones iniciales. Si los ceros del polinomio característico
\[p(s)=as^2+bs+c\nonumber \]
de la ecuación complementaria tienen partes reales negativas, entonces\(y_1\) y\(y_2\) ambas se acercan a cero como\(t\to\infty\), así que\(\lim_{t\to\infty}v(t)=0\) para cualquier elección de condiciones iniciales. Además, el valor de\(h(t)\) es esencialmente independiente de los valores de\(f(t-\tau)\) para grandes\(\tau\), ya que\(\lim_{\tau\to\infty}w(\tau)=0\). En este caso decimos que\(v\) y\(h\) son componentes transitorios y de estado estacionario, respectivamente, de la solución\(y\) de la Ecuación\ ref {eq:8.6.13}. Estas definiciones se aplican al problema de valor inicial de Example 8.6.4 , donde los ceros de
\[p(s)=s^2+2s+2=(s+1)^2+1\nonumber \]
son\(-1\pm i\). De la Ecuación\ ref {eq:8.6.10}, vemos que la solución del problema general del valor inicial del Ejemplo 8.6.4 es\(y=v+h\), donde
\[v(t)=e^{-t}\left((k_1+k_0)\sin t+k_0\cos t\right)\nonumber \]
es el componente transitorio de la solución y
\[h(t)=\int_0^t f(t-\tau)e^{-\tau}\sin\tau\,d\tau\nonumber \]
es el componente de estado estacionario. Las definiciones no se aplican a los problemas de valor inicial considerados en los Ejemplos 8.6.2 y 8.6.3 , ya que los ceros de los polinomios característicos en estos dos ejemplos no tienen partes reales negativas.
En aplicaciones físicas donde la entrada\(f\) y la salida\(y\) de un dispositivo están relacionadas por la ecuación\ ref {eq:8.6.13}, los ceros del polinomio característico suelen tener partes reales negativas. Entonces\(W={\cal L}(w)\) se llama la función de transferencia del dispositivo. Desde
\[H(s)=W(s)F(s),\nonumber \]
vemos que
\[W(s)={H(s)\over F(s)}\nonumber \]
es la relación entre la transformación de la salida de estado estacionario y la transformada de la entrada.
Debido a la forma de
\[h(t)=\int_0^tw(\tau)f(t-\tau)\,d\tau,\nonumber \]
\(w\)a veces se llama la función de ponderación del dispositivo, ya que asigna pesos a valores pasados de la entrada\(f\). También se llama la respuesta al impulso del dispositivo, por razones que se discuten en la siguiente sección.
La ecuación de fórmula\ ref {eq:8.6.14} se da con más detalle en los Ejercicios 8.6.8-8.6.10 para los tres casos posibles donde los ceros de\(p(s)\) son reales y distintos, reales y repetidos, o conjugados complejos, respectivamente.


