12.3: Ecuación de Laplace en coordenadas rectangulares
- Page ID
- 114765
La temperatura\(u=u(x,y,t)\) en una placa bidimensional satisface la ecuación bidimensional del calor
\[\label{eq:12.3.1} u_t=a^2(u_{xx}+u_{yy}),\]
donde\((x,y)\) varía sobre el interior de la placa y\(t>0\). Para encontrar una solución de la Ecuación\ ref {eq:12.3.1}, es necesario especificar la temperatura inicial\(u(x,y,0)\) y las condiciones que deben cumplirse en el límite. Sin embargo, como\(t\to\infty\), la influencia de la condición inicial decae, así
\[\lim_{t\to\infty}u_t(x,y,t)=0 \nonumber \]
y la temperatura se aproxima a una distribución de estado estacionario\(u=u(x,y)\) que satisface
\[\label{eq:12.3.2} u_{xx}+u_{yy}=0.\]
Esta es la ecuación de Laplace. Esta ecuación también surge en aplicaciones a la mecánica de fluidos y a la teoría del potencial; de hecho, también se le llama la ecuación de potencial. Buscamos soluciones de Ecuación\ ref {eq:12.3.2} en una región\(R\) que satisfaga condiciones especificadas —llamadas condiciones límite — en el límite de\(R\). Por ejemplo, podemos requerir\(u\) asumir valores prescritos en el límite. Esto se llama condición de Dirichlet, y el problema se llama problema de Dirichlet. O bien, podemos requerir que la derivada normal de\(u\) en cada punto\((x,y)\) del límite asuma los valores prescritos. Esto se llama condición de Neumann, y el problema se llama problema de Neumann. En algunos problemas imponemos condiciones de Dirichlet en parte del límite y condiciones de Neumann en el resto. Entonces decimos que las condiciones de contorno y el problema son mixtas.
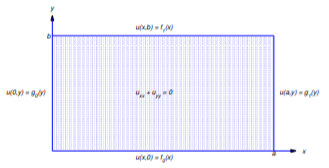
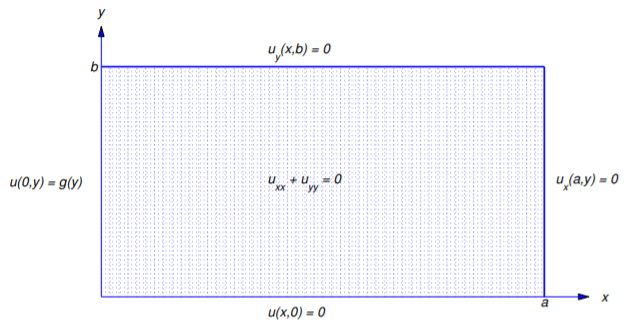
Resolver problemas de valor límite para la Ecuación\ ref {eq:12.3.2} sobre regiones generales está más allá del alcance de este libro, por lo que consideramos solo regiones muy simples. Comenzamos considerando la región rectangular que se muestra en la Figura 12.3.1 .

Las posibles condiciones de límite para esta región se pueden escribir como
\[\begin{array}{lcllll} (1-\alpha)u(x,0)&+&\alpha u_y(x,0)&=&f_0(x), &0\le x\le a,\\[4pt] (1-\beta) u(x,b)&+&\beta u_y(x,b)&=&f_1(x), &0\le x\le a,\\[4pt] (1-\gamma) u(0,y)&+&\gamma u_x(0,y)&=&g_0(y), &0\le y\le b,\\[4pt] (1-\delta) u(a,y)&+&\delta u_x(a,y)&=&g_1(y), &0\le y\le b, \end{array}\nonumber\]
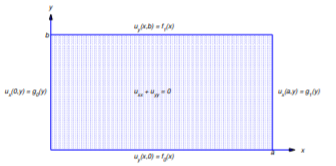
donde\(\alpha\),\(\beta\),\(\gamma\), y\(\delta\) puede ser cada uno\(0\) o\(1\); así, hay 16 posibilidades. Que BVP\((\alpha,\beta,\gamma,\delta)(f_0,f_1,g_0,g_1)\) denote el problema de encontrar una solución de la Ecuación\ ref {eq:12.3.2} que satisfaga estas condiciones. Este es un problema de Dirichlet si
\[\alpha=\beta=\gamma=\delta=0\nonumber\]
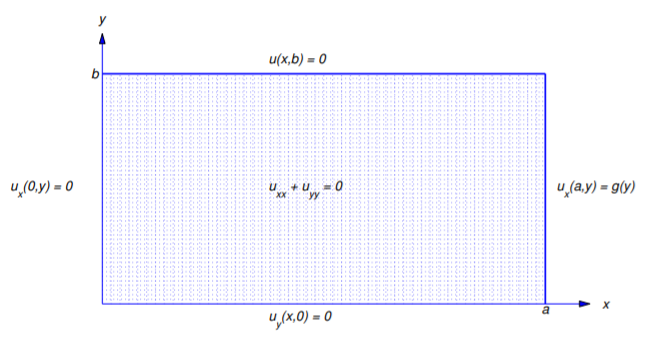
(Figura 12.3.2 ), o un problema de Neumann si
\[\alpha=\beta=\gamma=\delta=1\nonumber\]
(Figura 12.3.3 ). Los otros 14 problemas son mixtos.
Por dada\((\alpha,\beta,\gamma,\delta)\), la suma de soluciones de
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(f_0,0,0,0),\quad \mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,f_1,0,0),\nonumber\]
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,0,g_0,0), \quad \text{and} \quad \mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,0,0,g_1)\nonumber\]
es una solución de
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(f_0,f_1,g_0,g_1).\nonumber\]
Por lo tanto nos concentramos en problemas donde sólo una de las funciones\(f_0\)\(f_1\),\(g_0\),,\(g_2\) no es idéntica a cero. Hay 64 (¡cuéntalos!) problemas de esta forma. Cada uno tiene condiciones de contorno homogéneas en tres lados del rectángulo y una condición de límite no homogénea en el cuarto. Utilizamos la separación de variables para encontrar infinitamente muchas funciones que satisfacen la ecuación de Laplace y las tres condiciones de contorno homogéneas en el rectángulo abierto. Luego usamos estas soluciones como bloques de construcción para construir una solución formal de la ecuación de Laplace que también satisfaga la condición de límite no homogénea. Como no es factible considerar los 64 casos, limitaremos nuestra atención en el texto a sólo cuatro. Otros se discuten en los ejercicios.
Si\(v(x,y)=X(x)Y(y)\) entonces
\[v_{xx}+v_{yy}=X''Y+XY''=0\nonumber\]
para todos\((x,y)\) si y solo si
\[{X''\over X}=-{Y''\over Y}=k\nonumber\]
para todos\((x,y)\), donde\(k\) es una constante de separación. Esta ecuación es equivalente a
\[\label{eq:12.3.3} X''-kX=0,\quad Y''+kY=0.\]
A partir de aquí, la estrategia depende de las condiciones límite. Esto lo ilustramos con ejemplos.
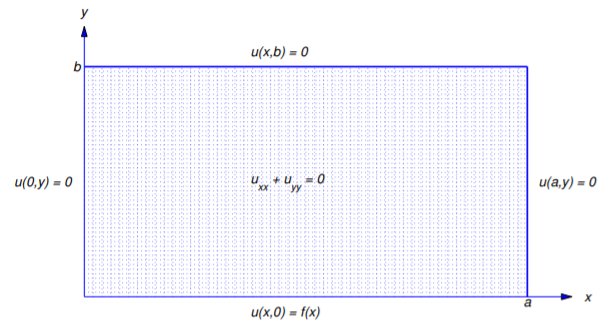
Definir la solución formal de
\[\label{eq:12.3.4} \begin{array}{ccc} {u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=f(x),}&{u(x,b)=0,}&{0\leq x\leq a,}\\{u(0,y)=0,}&{u(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figura 12.3.4 ).
Solución:
Las condiciones límite en la Ecuación\ ref {eq:12.3.4} requieren productos\(v(x,y)=X(x)Y(y)\) tales que\(X(0)=X(a)=Y(b)=0\); de ahí, dejamos\(k=-\lambda\) entrar la Ecuación\ ref {eq:12.3.3}. Por lo tanto,\(X\) y\(Y\) debe satisfacer
\[\label{eq:12.3.5} X''+\lambda X=0,\quad X(0)=0,\quad X(a)=0\]
y
\[\label{eq:12.3.6} Y''-\lambda Y=0,\quad Y(b)=0.\]
Del Teorema 11.1.2, los valores propios de la Ecuación\ ref {eq:12.3.5} son\(\lambda_n=n^2\pi^2/a^2\), con funciones propias asociadas
\[X_n=\sin{n\pi x\over a}, \quad n=1,2,3,\dots.\nonumber\]
Sustituyendo\(\lambda=n^2\pi^2/a^2\) en Ecuación\ ref {eq:12.3.6} rendimientos
\[Y''-(n^2\pi^2/a^2)Y=0,\quad Y(b)=0,\nonumber\]
para que pudiéramos tomar
\[\label{eq:12.3.7} Y_n=\sinh{n\pi(b-y)\over a};\]
sin embargo, debido a la condición de Dirichlet no homogénea en\(y=0\), es mejor exigirlo\(Y_n(0)=1\), lo que se puede lograr dividiendo el lado derecho de la Ecuación\ ref {eq:12.3.7} por su valor at\(y=0\); así, tomamos
\[Y_n={\sinh n\pi(b-y)/a\over\sinh n\pi b/a}.\nonumber\]
Entonces
\[v_n(x,y)=X_n(x)Y_n(y)={\sinh n\pi(b-y)/a\over\sinh n\pi b/a}\sin{n\pi x\over a},\nonumber\]
así\(v_n(x,0)=\sin n\pi x/a\) y\(v_n\) satisface la Ecuación\ ref {eq:12.3.4} con\(f(x)=\sin n\pi x/a\). De manera más general\(\alpha_1\), si,...,\(\alpha_m\) son constantes arbitrarias entonces
\[u_m(x,y)=\sum_{n=1}^m\alpha_n {\sinh n\pi(b-y)/a\over\sinh n\pi b/a} \sin{n\pi x\over a}\nonumber\]
satisface la Ecuación\ ref {eq:12.3.4} con
\[f(x)=\sum_{n=1}^m\alpha_n\sin{n\pi x\over L}.\nonumber\]
Por lo tanto, si\(f\) es una función lisa arbitraria por partes\([0,a]\), definimos la solución formal de la Ecuación\ ref {eq:12.3.4} para que sea
\[\label{eq:12.3.8} u(x,y)=\sum_{n=1}^\infty \alpha_n {\sinh n\pi(b-y)/a\over\sinh n\pi b/a} \sin{n\pi x\over a},\]
donde
\[S(x)=\sum_{n=1}^\infty \alpha_n\sin{n\pi x\over a}\nonumber\]
es la serie sinusoidal de Fourier de\(f\) on\([0,a]\); es decir,
\[\alpha_n={2\over a}\int_0^af(x)\sin{n\pi x\over a}\,dx,\quad n=1,2,3,\dots.\nonumber\]
Si\(y<b\) entonces
\[\label{eq:12.3.9} {\sinh n\pi(b-y)/a\over\sinh n\pi b/a}\approx e^{-n\pi y/a}\]
para grandes\(n\), así la serie en Ecuación\ ref {eq:12.3.8} converge si\(0< y < b\); además, ya que también
\[{\cosh n\pi(b-y)/a\over\sinh n\pi b/a}\approx e^{-n\pi y/a}\nonumber\]
para grandes\(n\), el Teorema 12.1.2 aplicado dos veces con\(z=x\) y dos veces con\(z=t\), demuestra que\(u_{xx}\) y se\(u_{yy}\) puede obtener diferenciando\(u\) término por término si\(0<y<b\)
Resolver Ecuación\ ref {eq:12.3.4} con\(f(x)=x(x^2-3ax+2a^2)\).
Solución
Del Ejemplo 11.3.6,
\[S(x)={12a^3\over\pi^3}\sum_{n=1}^\infty{1\over n^3}\sin{n\pi x\over a}.\nonumber\]
Por lo tanto
\[\label{eq:12.3.10} u(x,y)={12a^3\over\pi^3}\sum_{n=1}^\infty{\sinh n\pi(b-y)/a\over n^3\sinh n\pi b/a} \sin{n\pi x\over a}.\]
Para calcular valores aproximados de\(u(x,y)\), debemos usar sumas parciales de la forma
\[u_m(x,y)={12a^3\over\pi^3}\sum_{n=1}^m{\sinh n\pi(b-y)/a\over n^3\sinh n\pi b/a} \sin{n\pi x\over a}.\nonumber\]
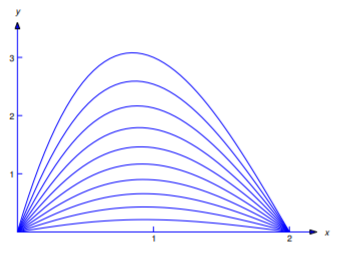
Debido a la ecuación\ ref {eq:12.3.9}, los valores pequeños de\(m\) proporcionan suficiente precisión para la mayoría de las aplicaciones si\(0<y<b\). Además, el\(n^{3}\) en el denominador en\ ref {eq:12.3.10} asegura que esto también es cierto para\(y = 0\). Para fines gráficos, elegimos\(a = 2, b = 1\), y\(m = 10\). La figura 12.3.5 muestra la superficie
\[u=u(x,y),\quad 0\le x\le 2,\quad 0\le y\le1,\nonumber\]
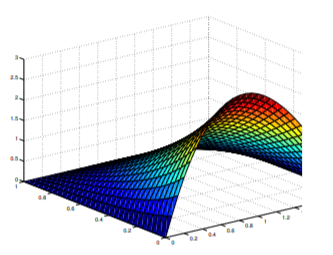
mientras que la Figura 12.3.6 muestra las curvas
\[u=u(x,0.1k),\quad 0\le x\le2,\quad k=0,1,\dots,10.\nonumber\]
Definir la solución formal de
\[\label{eq:12.3.11} \begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=0,}&{u_{y}(x,b)=f(x),}&{0\leq x\leq a,}\\{u_{x}(0,y)=0,}&{u_{x}(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figura 12.3.7 ).
Solución
Las condiciones límite en la Ecuación\ ref {eq:12.3.11} requieren productos\(v(x,y)=X(x)Y(y)\) tales que\(X'(0)=X'(a)=Y(0)=0\); de ahí, dejamos\(k=-\lambda\) entrar la Ecuación\ ref {eq:12.3.3}. Por lo tanto,\(X\) y\(Y\) debe satisfacer
\[\label{eq:12.3.12} X''+\lambda X=0,\quad X'(0)=0,\quad X'(a)=0\]
y
\[\label{eq:12.3.13} Y''-\lambda Y=0,\quad Y(0)=0.\]
Del Teorema 11.1.3, los valores propios de la Ecuación\ ref {eq:12.3.12} son\(\lambda=0\), con función propia asociada\(X_0=1\), y\(\lambda_n=n^2\pi^2/a^2\), con funciones propias asociadas
\[X_n=\cos{n\pi x\over a}, \quad n=1,2,3,\dots.\nonumber\]
Ya que\(Y_0=y\) satisface la Ecuación\ ref {eq:12.3.13} con\(\lambda=0\), tomamos\(v_0(x,y)=X_0(x)Y_0(y)= y\). Sustituyendo\(\lambda=n^2\pi^2/a^2\) en Ecuación\ ref {eq:12.3.13} rendimientos
\[Y''-(n^2\pi^2/a^2)Y=0,\quad Y(0)=0,\nonumber\]
para que pudiéramos tomar
\[\label{eq:12.3.14} Y_n=\sinh{n\pi y\over a}.\]
Sin embargo, debido a la condición de Neumann no homogénea en\(y=b\), es mejor requerirlo\(Y_n'(b)=1\), lo que se puede lograr dividiendo el lado derecho de la Ecuación\ ref {eq:12.3.14} por el valor de su derivada en\(y=b\); así,
\[Y_n={a\sinh n\pi y/a\over n\pi\cosh n\pi b/a}.\nonumber\]
Entonces
\[v_n(x,y)=X_n(x)Y_n(y)= {a\sinh n\pi y/a\over n\pi\cosh n\pi b/a}\cos{n\pi x\over a},\nonumber\]
por lo
\[{\partial v_n\over \partial y}(x,b)=\cos{n\pi x\over a}.\nonumber\]
Por lo tanto\(v_n\) satisface la Ecuación\ ref {eq:12.3.11} con\(f(x)=\cos n\pi x/a\). De manera más general\(\alpha_0\), si,...,\(\alpha_m\) son constantes arbitrarias entonces
\[u_m(x,y)=\alpha_0y+{a\over\pi}\sum_{n=1}^m\alpha_n {\sinh n\pi y/a\over n\cosh n\pi b/a} \cos{n\pi x\over a}\nonumber\]
satisface la Ecuación\ ref {eq:12.3.11} con
\[f(x)=\alpha_0+\sum_{n=1}^m\alpha_n\cos{n\pi x\over L}.\nonumber\]
Por lo tanto, si\(f\) es una función lisa arbitraria por partes en\([0,a]\) definimos la solución formal de la Ecuación\ ref {eq:12.3.11} para ser
\[u(x,y)=\alpha_0y+{a\over\pi}\sum_{n=1}^\infty \alpha_n {\sinh n\pi y/a\over n\cosh n\pi b/a} \cos{n\pi x\over a},\nonumber\]
donde
\[C(x)=\alpha_0+\sum_{n=1}^\infty \alpha_n\cos{n\pi x\over a}\nonumber\]
es la serie coseno de Fourier de\(f\) on\([0,a]\); es decir,
\[\alpha_0={1\over a}\int_0^af(x)\,dx \quad \text{and} \quad \alpha_n={2\over a}\int_0^af(x)\cos{n\pi x\over a}\,dx,\quad n=1,2,3,\dots.\nonumber\]
Resolver Ecuación\ ref {eq:12.3.11} con\(f(x)=x\).
Solución
Del Ejemplo 11.3.1,
\[C(x)=\frac{a}{2}-\frac{4a}{\pi ^{2}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{2}}\cos\frac{(2n-1)\pi x}{a}\nonumber\]
Por lo tanto
\[\label{eq:12.3.15} u(x,y)=\frac{ay}{2}-\frac{4a^{2}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{\sinh (2n-1)\pi y/a}{(2n-1)^{3}\cosh (2n-1)\pi b/a}\cos\frac{(2n-1)\pi x}{a}\]
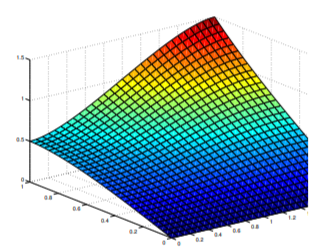
Para fines gráficos\(a=2\)\(b=1\), elegimos y conservamos los términos\(n=10\) en la Ecuación\ ref {eq:12.3.15}. La figura 12.3.8 muestra la superficie
\[u=u(x,y),\quad 0\le x\le 2,\quad 0\le y\le1,\nonumber\]
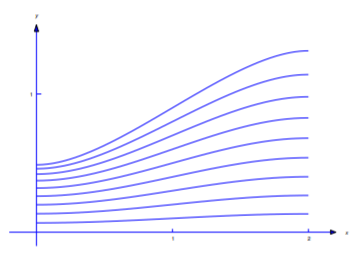
mientras que la Figura 12.3.9 muestra las curvas
\[u=u(x,.1k),\quad 0\le x\le2,\quad k=0,1,\dots,10.\nonumber\]
Definir la solución formal de
\[\label{eq:12.3.16} \begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=0,}&{u_{y}(x,b)=0,}&{0\leq x\leq a,}\\{u(0,y)=g(y),}&{u_{x}(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figura 12.3.10 ).
Solución
Las condiciones límite en la Ecuación\ ref {eq:12.3.16} requieren productos\(v(x,y)=X(x)Y(y)\) tales que\(Y(0)=Y'(b)=X'(a)=0\); por lo tanto, dejamos\(k=\lambda\) entrar la Ecuación\ ref {eq:12.3.3}. Por lo tanto,\(X\) y\(Y\) debe satisfacer
\[\label{eq:12.3.17} X''-\lambda X=0,\quad \quad X'(a)=0\]
y
\[\label{eq:12.3.18} Y''+\lambda Y=0,\quad Y(0)=0,\quad Y'(b)=0.\]
Del Teorema 11.1.4, los valores propios de la Ecuación\ ref {eq:12.3.18} son\(\lambda_n=(2n-1)^2\pi^2/4b^2\), con funciones propias asociadas
\[Y_n=\sin{(2n-1)\pi y\over2b}, \quad n=1,2,3,\dots.\nonumber\]
Sustituyendo\(\lambda=(2n-1)^2\pi^2/4b^2\) en Ecuación\ ref {eq:12.3.17} rendimientos
\[X''-((2n-1)^2\pi^2/4b^2)X=0,\quad X'(a)=0,\nonumber\]
para que pudiéramos tomar
\[\label{eq:12.3.19} X_n=\cosh{(2n-1)\pi(x-a)\over 2b}.\]
Sin embargo, debido a la condición de Dirichlet no homogénea en\(x=0\), es mejor requerirlo\(X_n(0)=1\), lo que se puede lograr dividiendo el lado derecho de la Ecuación\ ref {eq:12.3.19} por su valor at\(x=0\); así,
\[X_n= {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}.\nonumber\]
Entonces
\[v_n(x,y)=X_n(x)Y_n(y)= {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over2b},\nonumber\]
por lo
\[v_n(0,y)=\sin{(2n-1)\pi y\over2b}.\nonumber\]
Por lo tanto\(v_n\) satisface la Ecuación\ ref {eq:12.3.16} con\(g(y)=\sin(2n-1)\pi y/2b\). De manera más general\(\alpha_1\), si,...,\(\alpha_m\) son constantes arbitrarias entonces
\[u_m(x,y)=\sum_{n=1}^m \alpha_n {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over 2b}\nonumber\]
satisface la Ecuación\ ref {eq:12.3.16} con
\[g(y)=\sum_{n=1}^m \alpha_n\sin{(2n-1)\pi y\over2b}.\nonumber\]
Por lo tanto, si\(g\) es una función lisa arbitraria por partes\([0,b]\), definimos la solución formal de la Ecuación\ ref {eq:12.3.16} para que sea
\[u(x,y)=\sum_{n=1}^\infty \alpha_n {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over 2b},\nonumber\]
donde
\[S_M(x)=\sum_{n=1}^\infty \alpha_n\sin{(2n-1)\pi y\over2b}\nonumber\]
es la serie sinusoidal mixta de Fourier de\(g\) on\([0,b]\); es decir,
\[\alpha_n={2\over b}\int_0^bg(y)\sin{(2n-1)\pi y\over2b}\,dy.\nonumber\]
Resolver Ecuación\ ref {eq:12.3.16} con\(g(y)=y(2y^2-9by+12b^2)\).
Solución
Del Ejemplo 11.3.8,
\[S_{M}(y)=\frac{96b^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi y}{2b}\nonumber \]
Por lo tanto
\[u(x,y)=\frac{96b^{3}}{\pi ^{3}}\sum_{n=1}^{\infty }\frac{\cosh (2n-1)\pi (x-a)/2b}{(2n-1)^{3}\cosh (2n-1)\pi a/2b}\left [3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi y}{2b}\nonumber\]
Definir la solución formal de
\[\label{eq:12.3.20}\begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u_{y}(x,0)=0,}&{u(x,b)=0,}&{0\leq x\leq a,}\\{u_{x}(0,y)=0,}&{u_{x}(a,y)=g(y),}&{0\leq y\leq b}\end{array}\]
(Figura 12.3.11 ).
Solución:
Las condiciones límite en la Ecuación\ ref {eq:12.3.20} requieren productos\(v(x,y)=X(x)Y(y)\) tales que\(Y'(0)=Y(b)=X'(0)=0\); por lo tanto, dejamos\(k=\lambda\) entrar la Ecuación\ ref {eq:12.3.3}. Por lo tanto,\(X\) y\(Y\) debe satisfacer
\[\label{eq:12.3.21} X''-\lambda X=0,\quad \quad X'(0)=0\]
y
\[\label{eq:12.3.22} Y''+\lambda Y=0,\quad Y'(0)=0,\quad Y(b)=0.\]
Del Teorema 11.1.4, los valores propios de la Ecuación\ ref {eq:12.3.22} son\(\lambda_n=(2n-1)^2\pi^2/4b^2\), con funciones propias asociadas
\[Y_n=\cos{(2n-1)\pi y\over2b}, \quad n=1,2,3,\dots.\nonumber\]
Sustituyendo\(\lambda=(2n-1)^2\pi^2/4b^2\) en Ecuación\ ref {eq:12.3.21} rendimientos
\[X''-((2n-1)^2\pi^2/4b^2)X=0,\quad X'(0)=0,\nonumber\]
para que pudiéramos tomar
\[\label{eq:12.3.23} X_n=\cosh{(2n-1)\pi x\over 2b}.\]
Sin embargo, debido a la condición de Neumann no homogénea en\(x=a\), es mejor requerirlo\(X_n'(a)=1\), lo que se puede lograr dividiendo el lado derecho de la Ecuación\ ref {eq:12.3.23} por el valor de su derivada en\(x=a\); así,
\[X_n= {2b\cosh(2n-1)\pi x/2b\over(2n-1)\pi\sinh(2n-1)\pi a/2b}.\nonumber\]
Entonces
\[v_n(x,y)=X_n(x)Y_n(y)= {2b\cosh(2n-1)\pi x/2b\over(2n-1)\pi\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over2b},\nonumber\]
por lo
\[{\partial v_n\over\partial x}(a,y)=\cos{(2n-1)\pi y\over2b}.\nonumber\]
Por lo tanto\(v_n\) satisface la Ecuación\ ref {eq:12.3.20} con\(g(y)=\cos(2n-1)\pi y/2b\). De manera más general\(\alpha_1\), si,...,\(\alpha_m\) son constantes arbitrarias entonces
\[u_m(x,y)={2b\over\pi}\sum_{n=1}^m \alpha_n {\cosh(2n-1)\pi x/2b\over(2n-1)\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over 2b}\nonumber\]
satisface la Ecuación\ ref {eq:12.3.20} con
\[g(y)=\sum_{n=1}^\infty \alpha_n\cos{(2n-1)\pi y\over2b}.\nonumber\]
Por lo tanto, si\(g\) es una función lisa arbitraria por partes\([0,b]\), definimos la solución formal de la Ecuación\ ref {eq:12.3.20} para ser
\[u(x,y)={2b\over\pi}\sum_{n=1}^\infty \alpha_n {\cosh(2n-1)\pi x/2b\over(2n-1)\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over 2b},\nonumber\]
donde
\[C_M(y)=\sum_{n=1}^\infty \alpha_n\cos{(2n-1)\pi y\over2b}\nonumber\]
es la serie mixta de coseno de Fourier de\(g\) on\([0,b]\); es decir,
\[\alpha_n={2\over b}\int_0^bg(y)\cos{(2n-1)\pi y\over2b}\,dy.\nonumber\]
Resolver Ecuación\ ref {eq:12.3.20} con\(g(y)=y-b\).
Solución
Del Ejemplo 11.3.3,
\[C_M(y)=-{8b\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} \cos{(2n-1)\pi y\over2b}. \nonumber\]
Por lo tanto
\[u(x,y)=-{16b^2\over\pi^3}\sum_{n=1}^\infty{ \cosh(2n-1)\pi x/2b\over(2n-1)^3\sinh(2n-1)\pi a/2b} \cos{(2n-1)\pi y\over2b}.\nonumber\]
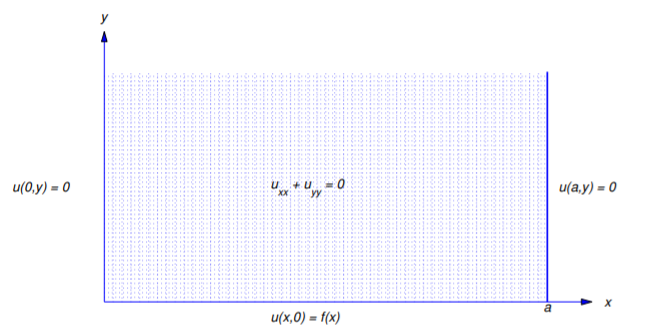
Ecuación de Laplace para una tira semi-infinita
Ahora buscamos soluciones de la ecuación de Laplace en la franja semi-infinita
\[S:\{ 0<x<a,\quad y>0\} \nonumber\]
(Figura 12.3.12 ) que satisfacen condiciones de límite homogéneas en\(x=0\) y\(x=a\), y una condición no homogénea de Dirichlet o Neumann en\(y=0\). Un ejemplo de tal problema es
\[\label{eq:12.3.24} \begin{array}{c} {u_{xx}+u_{yy}=0,\quad 0<x<a,\quad y>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq a,}\\{u(0,y)=0,\quad u(a,y)=0,\quad y>0,}\end{array}\]
Las condiciones límite en este problema no son suficientes para determinar\(u\), pues si\(u_0=u_0(x,y)\) es una solución y\(K\) es una constante entonces
\[u_1(x,y)=u_0(x,y)+K\sin{\pi x\over a}\sinh{\pi y\over a}.\nonumber\]
también es una solución. (Verificar.) No obstante, si también requerimos —por motivos físicos— que la solución quede delimitada para todos\((x,y)\) en\(S\) entonces\(K=0\) y se elimine esta dificultad.
Definir la solución formal acotada de la Ecuación\ ref {eq:12.3.24}.
Solución
Procediendo como en la solución del Ejemplo 12.3.1 , encontramos que las funciones de Building Block son de la forma
\[v_n(x,y)=Y_n(y)\sin{n\pi x\over a}, \nonumber\]
donde
\[Y_n''-(n^2\pi^2/a^2)Y_n=0. \nonumber\]
Por lo tanto
\[Y_n=c_1e^{n\pi y/a}+c_2e^{-n\pi y/a} \nonumber\]
donde\(c_1\) y\(c_2\) son constantes. Aunque las condiciones de contorno en la Ecuación\ ref {eq:12.3.24} no restringen\(c_1\)\(c_2\), y, debemos establecer\(c_1=0\) para asegurar que\(Y_n\) esté acotada. Dejar\(c_2=1\) rendimientos
\[v_n(x,y)=e^{-n\pi y/a}\sin{n\pi x\over a}, \nonumber\]
y definimos la solución formal acotada de la Ecuación\ ref {eq:12.3.24} como
\[u(x,y)=\sum_{n=1}^\infty b_ne^{-n\pi y/a}\sin{n\pi x\over a}, \nonumber\]
donde
\[S(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over a} \nonumber\]
es la serie sinusoidal de Fourier de\(f\) on\([0,a]\).
Consulte Ejercicios 12.3.29-12.3.34 para otros problemas de valor límite en una franja semiinfinita.


