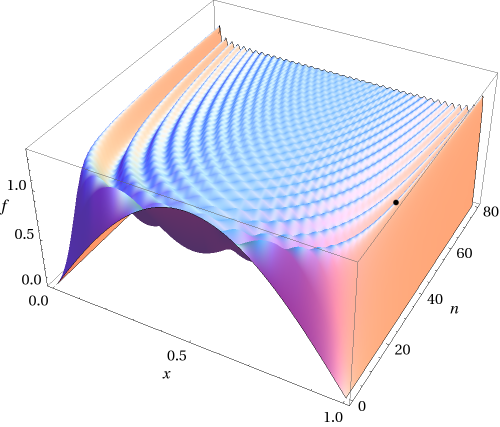
4.7: Convergencia de series de Fourier

Última actualización
Guardar como PDF

Page ID: 113722

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El tema final que consideraremos es la convergencia de las series de Fourier. Voy a mostrar dos ejemplos, estrechamente vinculados, pero con comportamientos radicalmente diferentes.

Figura\(\PageIndex{1}\): Las ondas cuadradas y triangulares en su dominio fundamental.

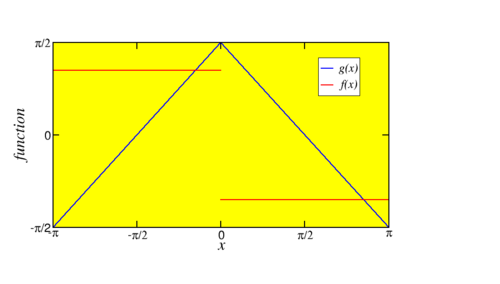
Una onda cuadrada,

\(f(x)= 1\)para\(-\pi < x < 0\);\(f(x)= -1\) para\(0 < x < \pi\).
una onda triangular,

\(g(x)= \pi/2+x\)para\(-\pi < x < 0\);\(g(x)= \pi/2-x\) para\(0 < x < \pi\).

Tenga en cuenta que\(f\) es el derivado de\(g\).

**Figura\(\PageIndex{2}\):** Una representación tridimensional del fenómeno de Gibbs para la onda cuadrada. El eje ortogonal al papel etiqueta el número de componentes de Fourier.

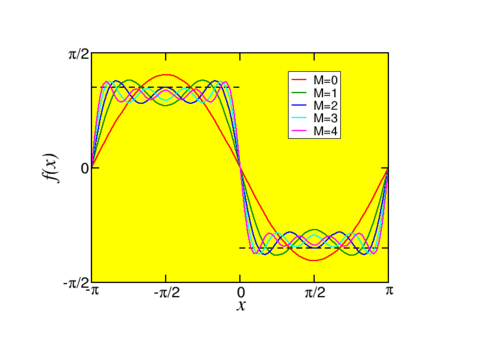
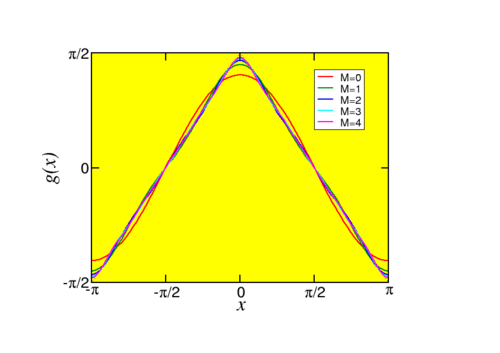
No es muy difícil encontrar la serie relevante de Fourier,\[\begin{aligned} f(x) & = & -\frac{4}{\pi} \sum_{m=0}^\infty \frac{1}{2m+1} \sin (2m+1) x,\\ g(x) & = & \frac{4}{\pi} \sum_{m=0}^\infty \frac{1}{(2m+1)^2} \cos (2m+1) x.\end{aligned} \nonumber \] Comparemos las sumas parciales, donde dejamos que la suma en la serie de Fourier corra de\(m=0\) a\(m=M\) en lugar de\(m=0\ldots\infty\). Observamos una marcada diferencia entre los dos casos. La convergencia de la serie de Fourier\(g\) es sin incidentes, y después de unos pasos es difícil ver una diferencia entre las sumas parciales, así como entre las sumas parciales y\(g\). Para\(f\), la onda cuadrada, vemos un resultado sorprendente: A pesar de que la aproximación se pone cada vez mejor en el medio (plano), hay un resultado finito (¡y constante!) rebasamiento cerca del salto. El área de este sobreimpulso se vuelve cada vez más pequeña a medida que aumentamos\(M\). A esto se le llama el fenómeno Gibbs (después de su descubridor). Se puede demostrar que para cualquier función con una discontinuidad tal efecto está presente, ¡y que el tamaño del sobreimpulso solo depende del tamaño de la discontinuidad! Una versión final, un poco más interesante de esta imagen, se muestra en la Fig. \(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Una representación tridimensional del fenómeno de Gibbs para la onda cuadrada. El eje ortogonal al papel etiqueta el número de componentes de Fourier.