5.6: Ecuaciones no homogéneas

Última actualización
Guardar como PDF

Page ID: 113667

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considera una varilla de longitud$2$ m, aislada lateralmente (el calor solo fluye dentro de la varilla). Inicialmente la temperatura$u$ es

\[\frac{1}{k}\sin\left( \frac{\pi x}{2} \right) + 500 \text{ K}. \nonumber \]

Los extremos izquierdo y derecho están ambos unidos a un termostato, y la temperatura en el lado izquierdo se fija a una temperatura de$500\text{ K}$ y el extremo derecho en$100\text{ K}$. También hay un calentador unido a la varilla que agrega un calor constante de$\sin\left( \frac{\pi x}{2}\right)$ a la varilla. La ecuación diferencial que describe esto no es homogénea

\[\begin{aligned} \dfrac{\partial}{\partial t} u &= k \dfrac{\partial^2}{\partial x^2} u + \sin\left(\frac{\pi x}{2}\right),\nonumber\\[4pt] u(0,t) &= 500,\nonumber\\[4pt] u(2,t) &= 100,\nonumber\\[4pt] u(x,0) &= \frac{1}{k}\sin\left( \frac{\pi x}{2} \right) + 500.\end{aligned} \nonumber \]

ince la inhomogeneidad es independiente del tiempo escribimos

\[u(x,t) = v(x,t) + h(x), \nonumber \]

donde$h$ se determinará de manera que se haga$v$ satisfacer una ecuación homogénea. Sustituyendo este formulario, encontramos

\[\dfrac{\partial}{\partial t} v = k \dfrac{\partial^2}{\partial x^2} v + k h'' + \sin\left( \frac{\pi x}{2} \right). \nonumber \]

Para hacer la ecuación para$v$ homogéneo requerimos\[h''(x) = - \frac{1}{k}\sin\left( \frac{\pi x}{2} \right), \nonumber \]

que tiene la solución

\[h(x) = C_1 x + C_2 + \frac{4}{k\pi^2}\sin\left( \frac{\pi x}{2} \right). \nonumber \]

Al mismo tiempo dejamos$h$ llevar las condiciones límite,$h(0)=500$,$h(2)=100$, y así\[h(x) = -{200} x + 500 + \frac{4}{k\pi^2}\sin\left( \frac{\pi x}{2} \right). \nonumber \] La función$v$ satisface

\[\begin{aligned} \dfrac{\partial}{\partial t} v &= k \dfrac{\partial^2}{\partial x^2} v, \nonumber\\[4pt] v(0,t) & = v(\pi,t) = 0, \nonumber\\[4pt] v(x,0) & = u(x,0) - h(x) = {200} x.\end{aligned} \nonumber \]

Este es un problema de un tipo que hemos visto antes. Por separación de variables encontramos

\[v(x,t) = \sum_{n=1}^\infty b_n \exp (- \frac{n^2\pi^2}{4}kt) \sin \frac{n\pi}{2}x. \nonumber \]

La condición inicial da

\[\sum_{n=1}^\infty b_n \sin nx = {200} x. \nonumber \]

de la que nos encontramos

\[b_n = (-1)^{n+1} \frac{800}{n\pi}. \nonumber \]

Y por lo tanto

\[u(x,t) = -\frac{200} x + 500 + \frac{4}{\pi^2 k} \sin \left(\frac{\pi x}{2}\right) + \frac{800}{\pi} \sum_{n=1}^\infty \frac{(-1)^n}{n+1} \sin \left(\frac{\pi nx}{2}\right) e^{-k (n \pi/2)^2 t}. \label{eq.10} \]

Nota: como$t\rightarrow \infty$,$u(x,t) \rightarrow -\frac{400}{\pi} x + 500 + \frac{\sin \frac{\pi}{2}x}{k}$. Como puede verse en la Fig. $\PageIndex{1}$este enfoque es bastante rápido —hemos elegido$k=1/500$ en esa cifra, y resumimos sobre las primeras 60 soluciones.

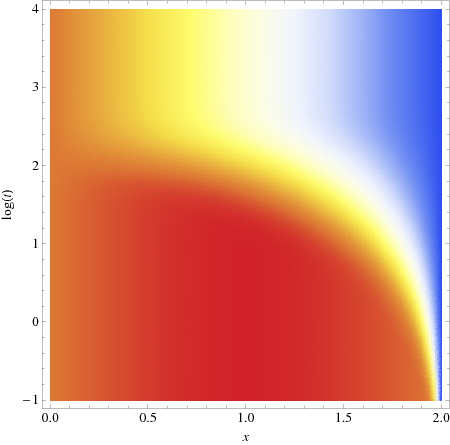
$Inhomgen2.png$

Figura$\PageIndex{1}$: Dependencia temporal de la solución a la ecuación no homogénea\ ref {eq.10}.