8.1: Ejemplo

Última actualización
Guardar como PDF

Page ID: 113805

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considera una placa circular de radio$c \text{ m}$, aislada desde arriba y abajo. La temperatura en la circunferencia está$100^\circ~\text{C}$ en la mitad del círculo, y$0^\circ~\text{C}$ en la otra mitad.

Figura$\PageIndex{1}$: Las condiciones límite para la temperatura en una placa circular.

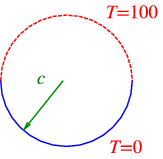
La ecuación diferencial a resolver es\[\rho^2 \frac{\partial^2 u}{\partial \rho^2} + \rho \frac{\partial u}{\partial \rho} + \frac{\partial^2 u}{\partial \phi^2}{u} = 0, \nonumber \] con condiciones de límite\[u(c,\phi) = \begin{cases} 100 & \text{if $0 < \phi < \pi$} \\ 0 & \text{if $\pi < \phi < 2\pi $} \end{cases}\quad . \nonumber \]

8.1.1: Periódica BC

No hay límite real en la$\phi$ dirección, pero introducimos uno, ya que elegimos dejar$\phi$ correr de$0$ a$2\pi$ solo. Entonces, ¿qué tipo de condiciones de límite aplicamos? Nos gustaría ver “comportamiento sin fisuras”, que especifica la periodicidad de la solución en$\phi$,\[\begin{aligned} u(\rho,\phi+2\pi)&=u(\rho,\phi),\\ \frac{\partial u}{\partial \phi}(\rho,\phi+2\pi)&=\frac{\partial u}{\partial \phi}(\rho,\phi).\end{aligned} \nonumber \] Si elegimos poner el parecer en$\phi=-\pi$ tenemos las condiciones de contorno periódicas\[\begin{aligned} u(\rho,2\pi)&=u(\rho,0),\\ \frac{\partial u}{\partial \phi}(\rho,2\pi)&=\frac{\partial u}{\partial \phi}(\rho,0).\end{aligned} \nonumber \]

Separamos las variables, y tomamos, como de costumbre\[u(\rho,\phi) = R(\rho) \Phi(\phi). \nonumber \] Esto da las ecuaciones diferenciales habituales\[\begin{aligned} \Phi''-\lambda\Phi &=0,\\ \rho^2 R'' + \rho R' + \lambda R &= 0.\end{aligned} \nonumber \] Nuestras condiciones de límite periódicas dan una condición sobre$\Phi$,\[\Phi(0)=\Phi(2\pi),\;\;\Phi'(0)=\Phi'(2\pi). \label{eq:phiBC} \] La otra condición límite involucra tanto$R$ y$\Phi$.