10.1: Temperatura en un Disco

Última actualización
Guardar como PDF

Page ID: 113687

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pasemos ahora a un problema bidimensional diferente. Se prepara un disco circular de tal manera que su temperatura inicial es radialmente simétrica,\[u(\rho,\phi,t=0) = f(\rho). \nonumber \] luego se coloca entre dos aisladores perfectos y su circunferencia se conecta a un congelador que lo mantiene en$0^\circ~\rm C$, como se esboza en la Fig. $\PageIndex{2}$.

$Una placa circular, aislada desde arriba y abajo.$

Figura$\PageIndex{1}$: Placa circular, aislada desde arriba y abajo.

Como las condiciones iniciales no dependen de$\phi$ ellas, esperamos que la solución también sea radialmente simétrica$u(\rho,t)$, lo que satisface la ecuación\[\begin{aligned} \frac{\partial u}{\partial t} &= k\left[\frac{\partial^2 u}{\partial \rho^2} + \frac{1}{\rho} \frac{\partial u}{\partial \rho} \right],\nonumber\\ u(c,t) &=0,\nonumber\\ u(\rho,0) &= f(\rho).\end{aligned} \nonumber \]

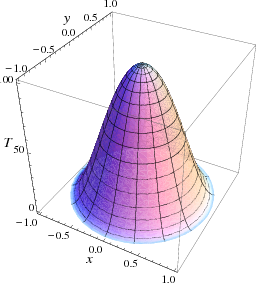
$La temperatura inicial en el disco.$

Figura$\PageIndex{2}$: La temperatura inicial en el disco.

Una vez más separamos las variables,$u(\rho,t)=R(\rho)T(t)$, lo que lleva a la ecuación

\[\frac{1}{k} \frac{T'}{T} = \frac{R''+\frac{1}{\rho}R'}{R} = -\lambda. \nonumber \]Esto corresponde a las dos ecuaciones

\[\begin{aligned} \rho^2 R''+\rho R' + \lambda \rho^2 R &= 0,\quad R(c)=0m\nonumber\\ T'+\lambda k T = 0.\end{aligned} \nonumber \]

La ecuación radial (que tiene un punto singular regular en$\rho=0$) está estrechamente relacionada con una de las ecuaciones más importantes de la física matemática, la ecuación de Bessel. Esta ecuación se puede llegar a partir de la sustitución$\rho = x /\sqrt{\lambda}$, para que con$R(r)=X(x)$ obtengamos la ecuación

\[x^2 \frac{d^2}{dx^2} X(x) + x \frac{d}{dx} X(x) + x^2 X(x) = 0, \qquad X(\sqrt \lambda c) =0. \nonumber \]