7.2: La ecuación logística
- Page ID
- 119657
En esta sección exploraremos un modelo poblacional simple no lineal. Por lo general, queremos modelar el crecimiento de una población determinada, y (t), y la ecuación diferencial que rige el comportamiento de crecimiento de esta población se desarrolla de manera similar a la utilizada anteriormente para mezclar problemas. A saber, observamos que la tasa de cambio de la población viene dada por una ecuación de la forma
\[\dfrac{d y}{d t}=\text { Rate In }-\text { Rate Out. }\nonumber \]
La Tasa In podría deberse al número de nacimientos por unidad de tiempo y a la Tasa de Salida por el número de muertes por unidad de tiempo. Si bien existen otras contribuciones potenciales a estas tasas consideraremos las tasas de natalidad y mortalidad en los ejemplos más simples.
Se puede obtener un modelo poblacional simple si se asume que estas tasas son lineales en la población. Así, suponemos que el
\[\text { Rate In }=b y \text { and the Rate Out }=my.\nonumber \]
Aquí hemos denotado la tasa de natalidad como\(b\) y la tasa de mortalidad como\(m .\) Esto da la tasa de cambio de la población como
\[\dfrac{d y}{d t}=b y-my \nonumber \]
(Crecimiento poblacional maltusiano). Generalmente, estas tasas podrían depender del tiempo. En el caso de que ambas sean tasas constantes, podemos definir\(k=b-m\) y obtener el modelo exponencial familiar de crecimiento poblacional:
\[\dfrac{d y}{d t}=k y \nonumber \]
Esto se resuelve fácilmente y se obtiene crecimiento\((k>0)\) o decaimiento exponencial\((k<0)\). Este modelo de crecimiento maltusiano lleva el nombre de Thomas Robert Malthus\((1766-1834)\), un clérigo que utilizó este modelo para advertir de la inminente fatalidad de la raza humana si sus prácticas reproductivas continuaban.
El modelo logístico se publicó\(18_{3} 8\) por primera vez en el modelo exponencial anterior toma la forma de Pierre François Verhulst (\(18 \mathrm{O} 4\)1849) en la forma
\[\dfrac{d N}{d t}=r N\left(1-\dfrac{N}{K}\right)\nonumber \]
donde\(N\) está la población en el momento\(t, r\) es la tasa de crecimiento, y\(K\) es lo que se llama la capacidad de carga. Tenga en cuenta que en nuestro modelo\(r=k=K c\).
Cuando las poblaciones se vuelven lo suficientemente grandes, hay competencia por los recursos, como el espacio y la comida, lo que puede llevar a una mayor tasa de mortalidad. Así, la tasa de mortalidad puede ser una función del tamaño de la población,\(m=m(y)\). El modelo más simple sería una dependencia lineal,\(m=\tilde{m}+c y .\) Entonces, el modelo exponencial anterior toma la forma
\[\dfrac{d y}{d t}=k y-c y^{2} \nonumber \]
donde A\(k=b-\tilde{m} .\) esto se le conoce como el modelo logístico de crecimiento poblacional. Por lo general,\(c\) es pequeño y el término no lineal agregado realmente no entra en acción hasta que la población se vuelve lo suficientemente grande.
Mostrar que la ecuación se\(\PageIndex{2}\) puede escribir en la forma
\[z^{\prime}=k z(1-z) \nonumber \]
que sólo tiene un parámetro.
Esto lo llevamos a cabo estar reescalando a la población\(y(t)=\alpha z(t)\),, dónde\(\alpha\) está por determinar. Insertando esta transformación, tenemos
\[\begin{aligned} y^{\prime} &=k y-c y^{2} \\ \alpha z^{\prime} &=\alpha k z-c \alpha^{2} z^{2} \end{aligned} \nonumber \]
O
\[z^{\prime}=k z\left(1-\alpha \dfrac{c}{k} z\right) \nonumber \]
Así, obtenemos el resultado,\(z^{\prime}=k z(1-z)\), si escogemos\(\alpha=\dfrac{k}{c}\).
Antes de obtener la solución exacta, es instructivo estudiar el comportamiento cualitativo de las soluciones sin anotar realmente ninguna solución explícita. Dichos métodos son útiles para ecuaciones no lineales más difíciles como veremos más adelante en este capítulo.
Demostraremos este análisis con un simple ejemplo de ecuación logística. Primero buscaremos soluciones constantes, llamadas soluciones de equilibrio, satisfactorias\(y^{\prime}(t)=0\). Luego, veremos el comportamiento de las soluciones cerca de las soluciones de equilibrio, o puntos fijos, y determinaremos la estabilidad de las soluciones de equilibrio. En la siguiente sección extenderemos estas ideas a otras ecuaciones diferenciales de primer orden.
Encontrar y clasificar las soluciones de equilibrio de la ecuación logística,
\[\dfrac{d y}{d t}=y-y^{2} \nonumber \]
Si dos soluciones de la ecuación diferencial se cruzan entonces tienen valores comunes\(y_{1}\) a la vez\(t_{1}\). Usando esta información, podríamos establecer un problema de valor inicial para el cual es la condición inicial\(y\left(t_{1}\right)=y_{1}\). Dado que las dos soluciones diferentes se cruzan en este punto en el plano de fase, tendríamos un problema de valor inicial con dos soluciones diferentes. Esto violaría el teorema de singularidad para problemas de valor inicial.
Primero, determinamos el equilibrio, o constante, soluciones dadas por\(y^{\prime}=0 .\) Para este caso, tenemos\(y-y^{2}=0 .\) Entonces, las soluciones de equilibrio son\(y=0\) y\(y=1\).
Estas soluciones dividen el plano ty en tres regiones,\(y<0,0<\)\(y<1\), y\(y>1\). Las soluciones que se originan en una de estas regiones\(t=t_{0}\) permanecerán en esa región para todos\(t>t_{0}\) ya que las soluciones de esta ecuación diferencial no pueden cruzarse.
A continuación, determinamos el comportamiento de las soluciones en las tres regiones. Al señalar que\(y^{\prime}(t)\) da la pendiente de cualquier solución en el plano, entonces encontramos que las soluciones son monótonas en cada región. Es decir, en regiones donde\(y^{\prime}(t)>0\), tenemos funciones monótonamente crecientes y en regiones donde\(y^{\prime}(t)<0\), tenemos funciones monótonamente decrecientes. Determinamos el signo de\(y^{\prime}(t)\) desde el lado derecho de la ecuación diferencial.
Por ejemplo, en este problema\(y-y^{2}>0\) sólo para la región media y\(y-y^{2}<0\) para las otras dos regiones. Así, la pendiente es positiva en la región media, dando una solución ascendente como se muestra en la Figura 7.1. Tenga en cuenta que esta solución no cruza las soluciones de equilibrio. Se pueden hacer declaraciones similares sobre las soluciones en las otras regiones.
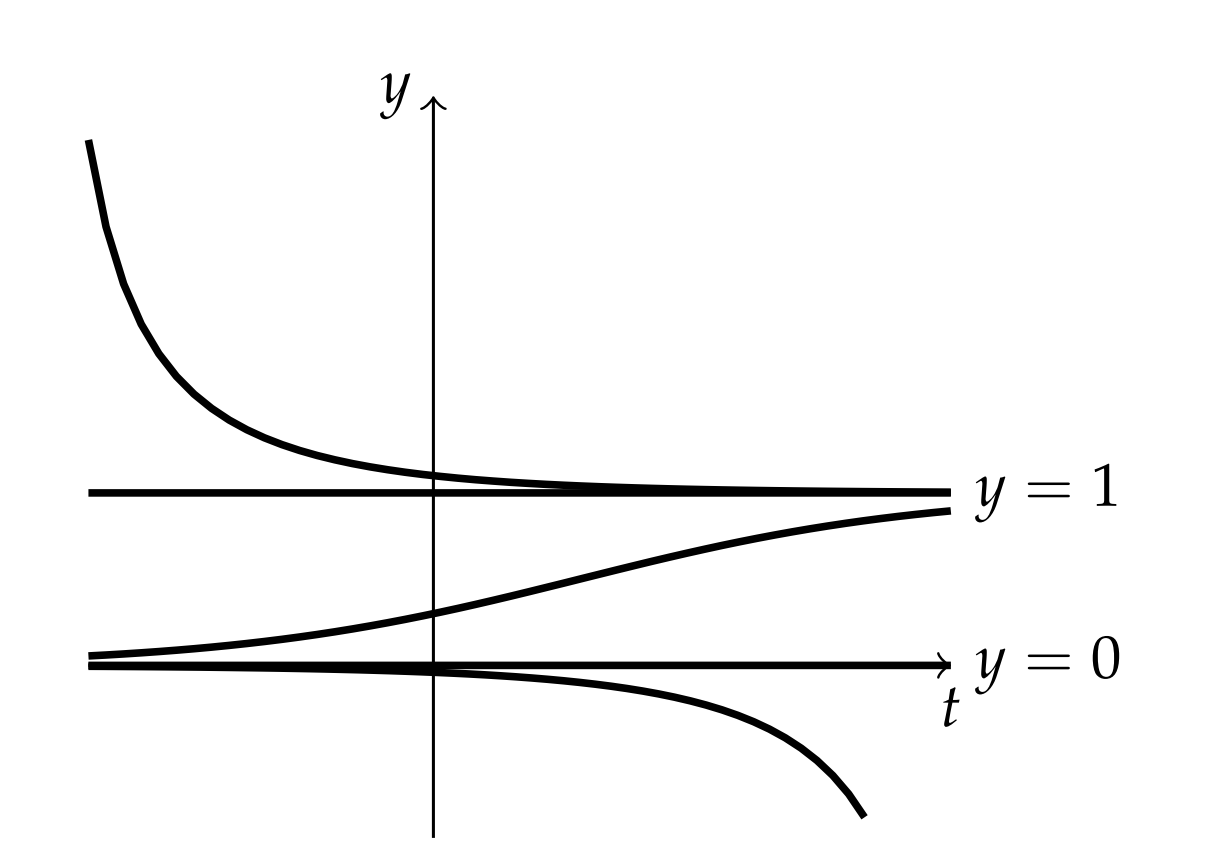
(Equilibrios estables e inestables). Observamos además que las soluciones a ambos lados de la solución de equilibrio\(y=1\) tienden a acercarse a esta solución de equilibrio para grandes valores de\(t\). De hecho, no importa cuán lejos estén estas soluciones\(y= 1\), siempre y cuando\(y(t)>0\), las soluciones eventualmente se acercarán a esta solución de equilibrio como\(t \rightarrow \infty\). Entonces decimos que la solución de equilibrio,\(y=1\), es un equilibrio estable.
De manera similar, observamos que las soluciones a ambos lados de la solución de\(y=0\) equilibrio\(y=0\) tienden a alejarse de grandes valores de\(t .\) No importa cuán cerca esté una solución\(y=0\) en algún momento dado, eventualmente estas soluciones divergirán como \(t \rightarrow \infty\). Decimos que tales soluciones de equilibrio son equilibrios inestables.
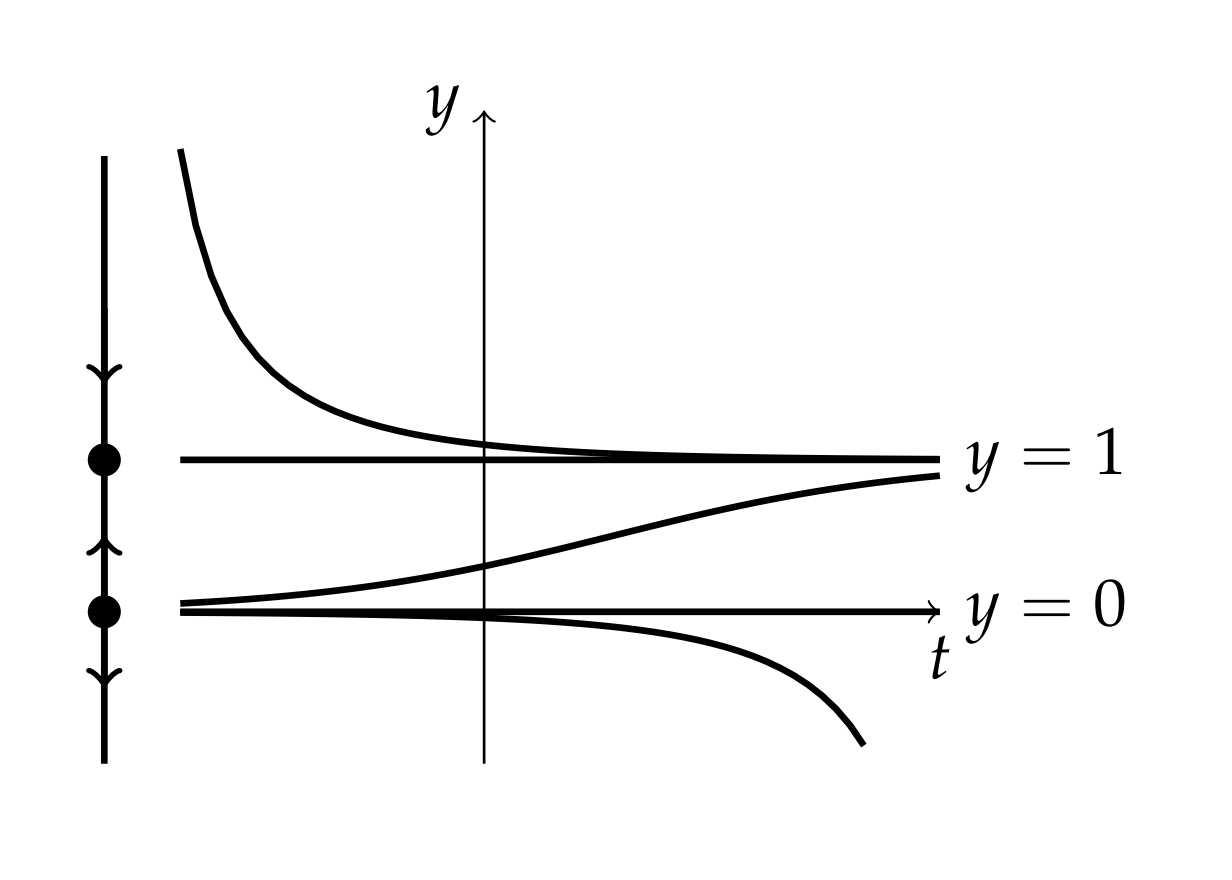
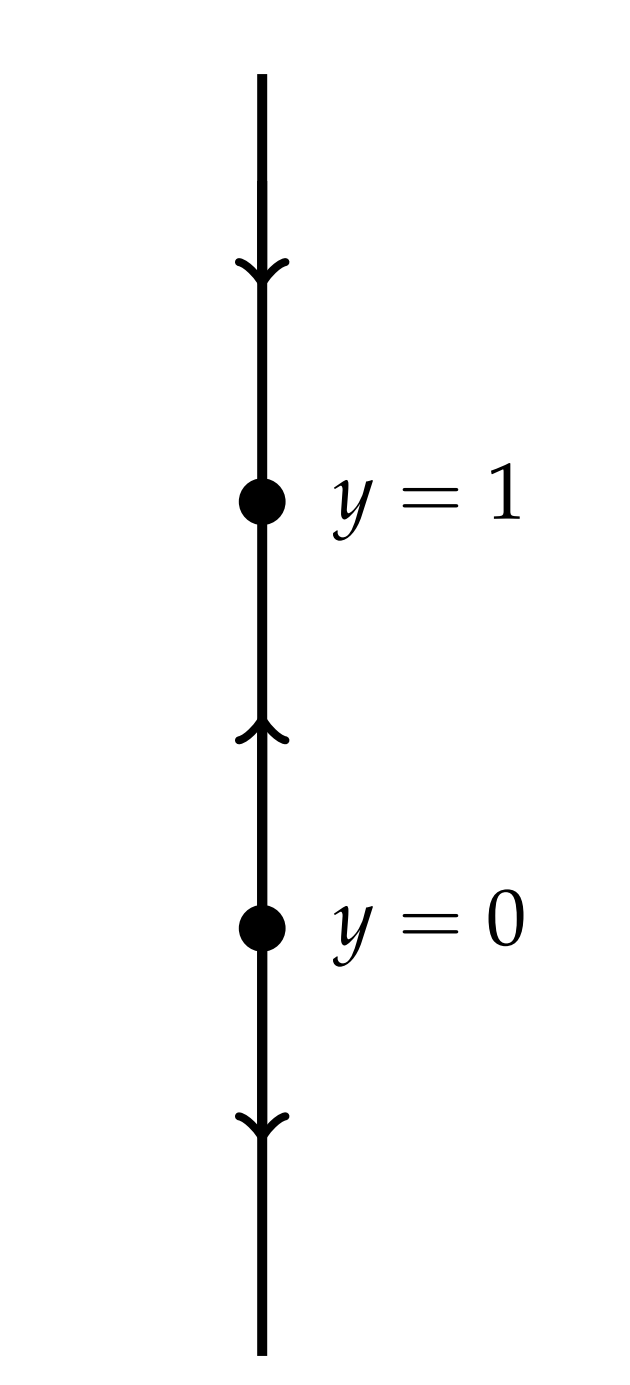
(Líneas de fase). Si solo nos interesa el comportamiento de las soluciones de equilibrio, podríamos simplemente mostrar una línea de fase. En la Figura\(\PageIndex{2}\) colocamos una línea vertical a la derecha de la gráfica del plano ty. En esta línea primero colocamos puntos en las soluciones de equilibrio correspondientes y etiquetamos las soluciones. Estos puntos dividen la línea de fase en tres intervalos.
En cada intervalo colocamos entonces flechas apuntando hacia arriba o hacia abajo indicando soluciones con pendientes positivas o negativas, respectivamente. Por ejemplo, para el intervalo\(y>1\) hay una flecha que apunta hacia abajo que indica que la pendiente es negativa en esa región.
Mirando la línea de fase resultante podemos determinar si un equilibrio dado es estable (flechas apuntando hacia el punto) o inestable (flechas que apuntan lejos del punto). En Figura\(\PageIndex{3}\) dibujamos la línea de fase final por sí misma. Vemos que\(y=1\) es un punto de equilibrio estable y\(y=0\) es un punto de equilibrio inestable.
La ecuación de Riccati
HEMOS VISTO QUE NO SE NECESITA una solución explícita de la Ecuación\(\PageIndex{2}\) logística para estudiar el comportamiento de sus soluciones. Sin embargo, la ecuación logística es un ejemplo de una ecuación no lineal de primer orden que es solucionable. También es un ejemplo de una ecuación general de Riccati, una ecuación diferencial de primer orden cuadrática en la función desconocida.
La ecuación de Riccati lleva el nombre del matemático italiano Jacopo Francesco Riccati\((1676-1754)\). Cuando\(a(t)=0\), la ecuación se convierte en una ecuación de Bernoulli.
La forma general de la ecuación de Riccati es
\[\dfrac{d y}{d t}=a(t)+b(t) y+c(t) y^{2} \nonumber \]
Siempre y cuando\(c(t) \neq 0\), esta ecuación se pueda reducir a una ecuación diferencial lineal de segundo orden a través de la transformación
\[y(t)=-\dfrac{1}{c(t)} \dfrac{x^{\prime}(t)}{x(t)}.\nonumber \]
Demostraremos el uso de esta transformación en la obtención de la solución de la ecuación logística.
Resolver la ecuación logística
\[\dfrac{d y}{d t}=k y-c y^{2} \nonumber \]
usando la transformación
\[y=\dfrac{1}{c} \dfrac{x^{\prime}}{x}\nonumber \]
diferenciando esta transformación con respecto a\(t\), obtenemos
\[ \begin{aligned} \dfrac{d y}{d t} &=\dfrac{1}{c}\left[\dfrac{x^{\prime \prime}}{x}-\left(\dfrac{x^{\prime}}{x}\right)^{2}\right] \\ &=\dfrac{1}{c}\left[\dfrac{x^{\prime \prime}}{x}-(c y)^{2}\right] \\ &=\dfrac{1}{c} \dfrac{x^{\prime \prime}}{x}-c y^{2} \end{aligned} \label{7.6} \]
Insertando este resultado en la ecuación logística\(\PageIndex{5}\), tenemos
\[\dfrac{1}{c} \dfrac{x^{\prime \prime}}{x}-c y^{2}=k \dfrac{1}{c}\left(\dfrac{x^{\prime}}{x}\right)-c y^{2}. \nonumber \]
Simplificando, vemos que la ecuación logística se ha reducido a una ecuación diferencial lineal de segundo orden,
\[x^{\prime \prime}=k x^{\prime}\nonumber \]
Esta ecuación se resuelve fácilmente. Una integración da
\[x^{\prime}(t)=B e^{k t}.\nonumber \]
Una segunda integración da
\[x(t)=A+B e^{k t}\nonumber \]
donde\(A\) y\(B\) son dos constantes arbitrarias.
Insertando este resultado en la transformación de Riccati, obtenemos
\[y(t)=\dfrac{1}{c} \dfrac{x^{\prime}}{x}=\dfrac{k B e^{k t}}{c\left(A+B e^{k t}\right)}\nonumber \]
Parece que tenemos dos constantes arbitrarias. Sin embargo, comenzamos con una ecuación diferencial de primer orden y por lo tanto solo esperamos una constante arbitraria. Podemos resolver este dilema dividiendo\(^{1}\) el numerador y el denominador por\(B e^{k t}\) y definiendo\(C=\dfrac{A}{B} .\) Entonces, tenemos la solución
\[y(t)=\dfrac{k / c}{1+C e^{-k t}} \nonumber \]
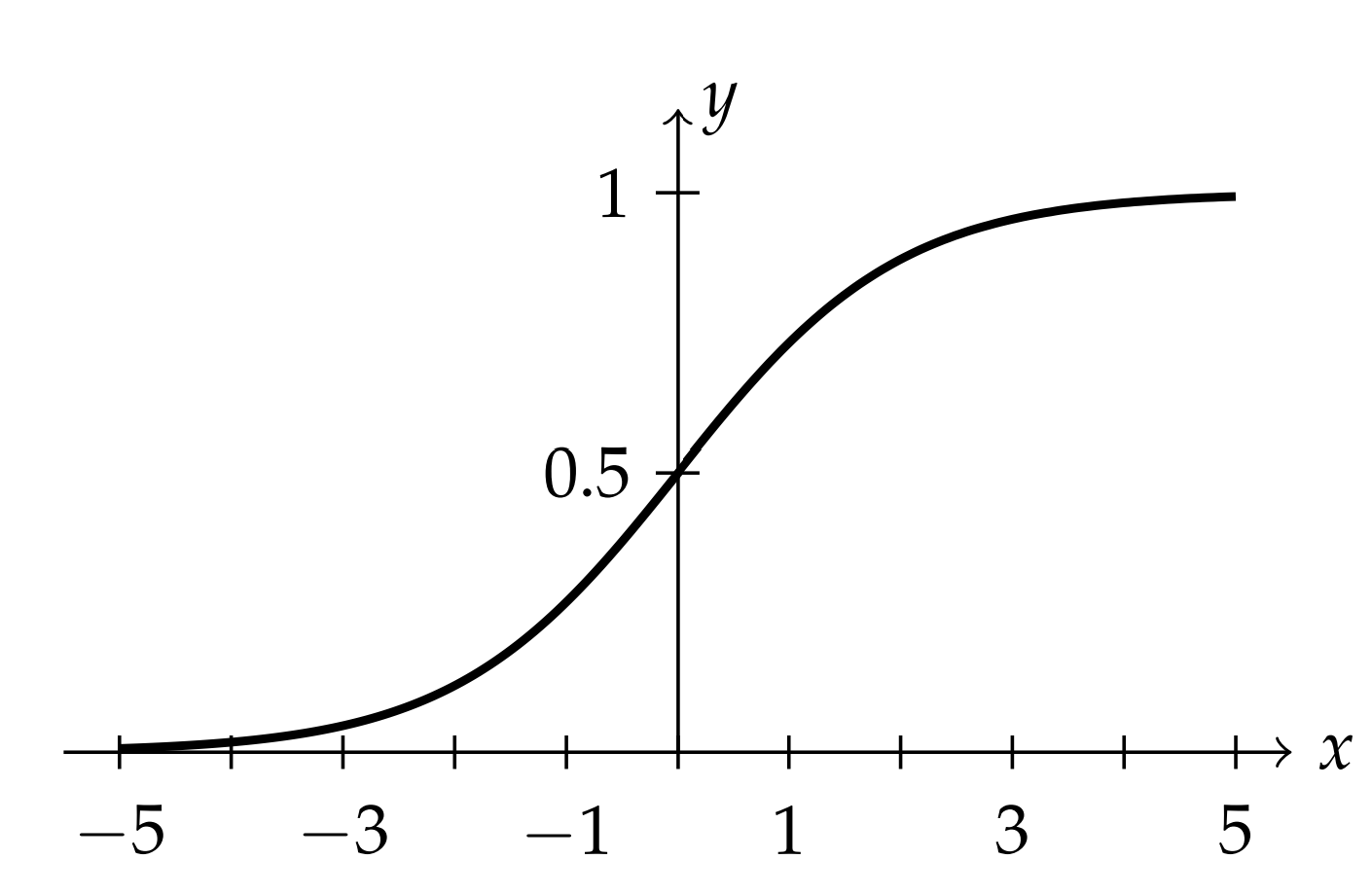
demostrando que en realidad sólo hay una constante arbitraria en la solución. Gráficas de la solución\(\PageIndex{7}\) de la ecuación logística para diferentes condiciones iniciales da las soluciones vistas en la última sección. En particular, fijando todas las constantes a la unidad, tenemos la función sigmoide,
\[y(t)=\dfrac{1}{1+e^{-t}}.\nonumber \]
Esta es la curva\(S\) en forma de firma del modelo logístico como se muestra en la Figura\(\PageIndex{4}\). Cabe señalar que esta no es la única manera de obtener la solución a la ecuación logística, aunque este enfoque nos ha proporcionado una introducción a las ecuaciones de Riccati. Un enfoque más directo sería utilizar la separación de variables en la ecuación logística, que es el Problema 1.
- 1
-
Esta solución general se sostiene para\(B \neq 0\). Si\(B=0\), entonces tenemos\(x(t)=A\) y, así,\(y(t)\) es la solución de equilibrio constante.


