8.5: Integrales
- Page ID
- 119777
La integración suele ser un poco más difícil. Imagínese que se le da el último resultado en la Ecuación 8.4.2 y tener que averiguar qué se diferenció para obtener la función dada. Como recordarás del Teorema Fundamental del Cálculo, la integral es la operación inversa a la diferenciación:
\[\int \dfrac{d f}{d x} d x=f(x)+C \nonumber \]
No siempre es fácil evaluar una integral dada. De hecho, ¡algunas integrales ni siquiera son factibles! No obstante, aprendiste en cálculo que existen algunos métodos que podrían dar respuesta. Si bien puede ser más feliz usando un sistema de álgebra por computadora, como Maple o Wolframalpha.com, o una calculadora elegante, debe conocer algunas integrales básicas y saber cómo usar tablas para algunas de las más complicadas. De hecho, puede ser estimulante cuando se puede hacer una integral dada sin hacer referencia a una computadora o una Tabla de Integrales. No obstante, debes estar preparado para hacer algunas integrales usando lo que te han enseñado en cálculo. Revisaremos algunos de estos métodos y algunas de las integrales estándar en esta sección.
En primer lugar, hay algunas integrales que se espera que conozcas sin hacer ningún trabajo. Estas integrales aparecen a menudo y son solo una aplicación del Teorema Fundamental del Cálculo al Cuadro 8.4.1 anterior. Las integrales básicas que los estudiantes deben conocer de la parte superior de sus cabezas se dan en Tabla\(\PageIndex{1}\).
Estas no son las únicas integrales que deberías poder hacer. Podemos ampliar la lista recordando algunas de las técnicas que aprendiste en cálculo, el Método de Sustitución, Integración por Partes, integración mediante descomposición parcial de fracciones e integrales trigonométricas y sustitución trigonométrica. También hay algunas otras técnicas que no habías visto antes. Veremos varios ejemplos.
Evaluar\(\int \dfrac{x}{\sqrt{x^{2}+1}} d x\).
Solución
Cuando te enfrentas a una integral, primero debes preguntar si una simple sustitución reduciría la integral a una que sabes hacer.
La parte fea de esta integral es la de\(x^{2}+1\) debajo de la raíz cuadrada. Entonces, dejamos\(u=x^{2}+1\).
Señalando que cuando\(u=f(x)\), tenemos\(d u=f^{\prime}(x) d x .\) Por nuestro ejemplo,\(d u=2 x d x\).
Mirando lo integral, parte del integrando se puede escribir como\(x d x=\dfrac{1}{2} u d u\). Entonces, la integral se convierte
\[\int \dfrac{x}{\sqrt{x^{2}+1}} d x=\dfrac{1}{2} \int \dfrac{d u}{\sqrt{u}} \nonumber \]
La sustitución ha convertido nuestra integral en una integral sobre\(u\). Además, ¡esta integral es factible! Es una de las integrales que debemos conocer. A saber, podemos escribirlo como
\[\dfrac{1}{2} \int \dfrac{d u}{\sqrt{u}}=\dfrac{1}{2} \int u^{-1 / 2} d u\nonumber \]
Esto ahora se termina fácilmente después de integrar y usar la variable de sustitución para dar
\[\int \dfrac{x}{\sqrt{x^{2}+1}} d x=\dfrac{1}{2} \dfrac{u^{1 / 2}}{\dfrac{1}{2}}+C=\sqrt{x^{2}+1}+C.\nonumber \]
Tenga en cuenta que hemos agregado la constante de integración requerida y que la derivada del resultado da fácilmente el integrando original (después de emplear la Regla de Cadena).
Muchas veces nos encontramos ante integrales definidas, en las que nos integramos entre dos límites. Hay varias formas de usar estos límites. Sin embargo, los estudiantes suelen olvidar que un cambio de variables generalmente significa que los límites tienen que cambiar.
| Función | Integral indefinida |
|---|---|
| \(a\) | \(a x\) |
| \(x^{n}\) | \(\dfrac{x^{n+1}}{n+1}\) |
| \(e^{a x}\) | \(\dfrac{1}{a} e^{a x}\) |
| \(\dfrac{1}{x}\) | \(\ln x\) |
| \(\sin a x\) | \(-\dfrac{1}{a} \cos a x\) |
| \(\cos a x\) | \(\dfrac{1}{a} \sin a x\) |
| \(\sec ^{2} a x\) | \(\dfrac{1}{a} \tan a x\) |
| \(\sinh a x\) | \(\dfrac{1}{a} \cosh a x\) |
| \(\cosh a x\) | \(\dfrac{1}{a} \sinh a x\) |
| \(\operatorname{sech}^{2} a x\) | \(\dfrac{1}{a} \tanh a x\) |
| \(\sec x\) | \(\ln |\sec x+\tan x|\) |
| \(\dfrac{1}{a+b x}\) | \(\dfrac{1}{b} \ln (a+b x)\) |
| \(\dfrac{1}{a^{2}+x^{2}}\) | \(\dfrac{1}{a} \tan ^{-1} \dfrac{x}{a}\) |
| \(\dfrac{1}{\sqrt{a^{2}-x^{2}}}\) | \(\sin ^{-1} \dfrac{x}{a}\) |
| \(\dfrac{1}{x \sqrt{x^{2}-a^{2}}}\) | \(\dfrac{1}{a} \sec ^{-1} \dfrac{x}{a}\) |
| \(\dfrac{1}{\sqrt{x^{2}-a^{2}}}\) | \(\cosh ^{-1} \dfrac{x}{a}=\ln \left|\sqrt{x^{2}-a^{2}}+x\right|\) |
Evaluar\(\int_{0}^{2} \dfrac{x}{\sqrt{x^{2}+1}} d x\).
Solución
Este es el último ejemplo pero con límites de integración añadidos. Procedemos como antes. Dejamos\(u=x^{2}+1\). Como\(x\) va de o a\(2, u\) toma valores de i a\(5 .\) Así, esta sustitución da
\[\int_{0}^{2} \dfrac{x}{\sqrt{x^{2}+1}} d x=\dfrac{1}{2} \int_{1}^{5} \dfrac{d u}{\sqrt{u}}=\left.\sqrt{u}\right|_{1} ^{5}=\sqrt{5}-1 \nonumber \]
Cuando se vuelve competente en la integración, puede omitir algunos de estos pasos. En el siguiente ejemplo intentamos demostrar el proceso de pensamiento involucrado en el uso de la sustitución sin usar explícitamente la variable de sustitución.
Evaluar\(\int_{0}^{2} \dfrac{x}{\sqrt{9+4 x^{2}}} d x\).
Solución
Al igual que con el ejemplo anterior, se ve que la derivada de\(9+4 x^{2}\) es proporcional a\(x\), que está en el numerador del integrando. Así una sustitución daría un integrando de la forma\(u^{-1 / 2} .\) Entonces, esperamos que la respuesta sea proporcional a\(\sqrt{u}=\sqrt{9+4 x^{2}}\). El punto de partida es, por lo tanto,
\[\int \dfrac{x}{\sqrt{9+4 x^{2}}} d x=A \sqrt{9+4 x^{2}}\nonumber \]
donde\(A\) es una constante por determinar.
Podemos determinar\(A\) a través de la diferenciación ya que la derivada de la respuesta debe ser el integrando. Por lo tanto,
\[ \begin{aligned} \dfrac{d}{d x} A\left(9+4 x^{2}\right)^{\dfrac{1}{2}} &=A\left(9+4 x^{2}\right)^{-\dfrac{1}{2}}\left(\dfrac{1}{2}\right)(8 x) \\ &=4 x A\left(9+4 x^{2}\right)^{-\dfrac{1}{2}} \end{aligned} \label{A.60} \]
Comparando este resultado con el integrando, vemos que el integrando se obtiene cuando\(A=\dfrac{1}{4}\). Por lo tanto,
\[\int \dfrac{x}{\sqrt{9+4 x^{2}}} d x=\dfrac{1}{4} \sqrt{9+4 x^{2}} \nonumber \]
Ahora completamos la integral,
\[\int_{0}^{2} \dfrac{x}{\sqrt{9+4 x^{2}}} d x=\dfrac{1}{4}[5-3]=\dfrac{1}{2}\nonumber \]
La función\(\operatorname{gd}(x)=\int_{0}^{x} \dfrac{d x}{\cosh x}=2 \tan ^{-1} e^{x}-\dfrac{\pi}{2}\) se llama Gudermannian y conecta funciones trigonométricas e hiperbólicas. Esta función lleva el nombre de Christoph Gudermann (1798-1852), pero introducida por Johann Heinrich Lambert (\(1728-1777\)), quien fue uno de los primeros en introducir funciones hiperbólicas.
Evaluar\(\int \dfrac{d x}{\cosh x}\).
Solución
Esta integral se puede realizar usando primero la definición de\(\cosh x\) seguida de una simple sustitución.
\[ \begin{aligned} \int \dfrac{d x}{\cosh x} &=\int \dfrac{2}{e^{x}+e^{-x}} d x \\ &=\int \dfrac{2 e^{x}}{e^{2 x}+1} d x \end{aligned} \label{A.61} \]
Ahora, dejamos\(u=e^{x}\) y\(d u=e^{x} d x\). Entonces,
\[ \begin{aligned} \int \dfrac{d x}{\cosh x} &=\int \dfrac{2}{1+u^{2}} d u \\ &=2 \tan ^{-1} u+C \\ &=2 \tan ^{-1} e^{x}+C \end{aligned} \label{A.62} \]
Integración por Partes
Cuando falla el Método de Sustitución, hay otros métodos que puedes probar. Uno de los más utilizados es el Método de Integración por Partes. Recuérdese la Fórmula de Integración por Partes:
\[\int u d v=u v-\int v d u \nonumber \]
La idea detrás de Integrar por Partes es que se te dé la integral a la izquierda y puedas relacionarla con una integral a la derecha. Ojalá que la nueva integral sea una que puedas hacer, o al menos es una integral más fácil que la que estás tratando de evaluar.
Sin embargo, no se le suelen dar las funciones\(u\) y\(v\). Hay que determinarlos. La forma integral que realmente tienes es función de otra variable, digamos\(x\). Otra forma de la Fórmula de Integración por Partes se puede escribir como
\[\int f(x) g^{\prime}(x) d x=f(x) g(x)-\int g(x) f^{\prime}(x) d x \nonumber \]
Nota: A menudo en física se necesita mover una derivada entre funciones dentro de un integrando. La clave - utilizar la integración por partes para mover la derivada de una función a la otra bajo una integral.
Esta forma es un poco más complicada en apariencia, aunque es más clara que la\(u-v\) forma en cuanto a lo que está sucediendo. La derivada se ha movido de una función a otra. Recordemos que esta fórmula se derivó integrando la regla del producto para la diferenciación. Estas dos fórmulas pueden relacionarse mediante el uso de las relaciones diferenciales
\[ \begin{aligned} &u=f(x) \quad \rightarrow \quad d u=f^{\prime}(x) d x \\ &v=g(x) \quad \rightarrow \quad d v=g^{\prime}(x) d x \end{aligned} \label{A.65} \]
Esto también da un método para aplicar la Fórmula de Integración por Partes.
Considerar la integral\(\int x \sin 2 x d x .\)
Solución
Elegimos\(u=x\) y\(d v=\sin 2 x d x .\) Esto da el lado izquierdo correcto de la Fórmula de Integración por Partes. A continuación determinamos\(v\) y\(d u\):
\[\begin{gathered} d u=\dfrac{d u}{d x} d x=d x \\ v=\int d v=\int \sin 2 x d x=-\dfrac{1}{2} \cos 2 x \end{gathered} \nonumber \]
Observamos que normalmente no se necesita la constante de integración. Insertando estas expresiones en la Fórmula de Integración por Partes, tenemos
\[\int x \sin 2 x d x=-\dfrac{1}{2} x \cos 2 x+\dfrac{1}{2} \int \cos 2 x d x \nonumber \]
Vemos que la nueva integral es más fácil de hacer que la integral original. Si hubiéramos escogido\(u=\sin 2 x\) y\(d v=x d x\), entonces la fórmula sigue funcionando, pero la integral resultante no es más fácil.
Para completar, terminamos la integración. El resultado es
\[\int x \sin 2 x d x=-\dfrac{1}{2} x \cos 2 x+\dfrac{1}{4} \sin 2 x+C.\nonumber \]
Como siempre, puedes verificar tu respuesta diferenciando el resultado, un paso que los alumnos suelen olvidar hacer. A saber,
\[ \begin{aligned} \dfrac{d}{d x}\left(-\dfrac{1}{2} x \cos 2 x+\dfrac{1}{4} \sin 2 x+C\right)&=-\dfrac{1}{2} \cos 2 x+x \sin 2 x+\dfrac{1}{4}(2 \cos 2 x) \\ & =x \sin 2 x \text {. } \end{aligned} \label{A.66} \]
Entonces, sí recuperamos el integrando en la integral original.
(Integración por Partes para Integrales Definitivas). También podemos realizar la integración por partes en integrales definidas. La fórmula general está escrita como
\[\int_{a}^{b} f(x) g^{\prime}(x) d x=\left.f(x) g(x)\right|_{a} ^{b}-\int_{a}^{b} g(x) f^{\prime}(x) d x \nonumber \]
Considerar la integral
\[\int_{0}^{\pi} x^{2} \cos x d x \nonumber \]
Esto requerirá dos integraciones por partes. Primero, dejamos\(u=x^{2}\) y\(d v=\cos x .\) luego,
\[d u=2 x d x . \quad v=\sin x\nonumber \]
Insertando en la Fórmula de Integración por Partes, tenemos
\[ \begin{aligned} \int_{0}^{\pi} x^{2} \cos x d x &=\left.x^{2} \sin x\right|_{0} ^{\pi}-2 \int_{0}^{\pi} x \sin x d x \\ &=-2 \int_{0}^{\pi} x \sin x d x \end{aligned} \label{A.68} \]
Observamos que la integral resultante es más fácil que la integral dada, pero todavía no podemos hacer la integral de la parte superior de nuestra cabeza (a menos que miremos Ejemplo\(3 !\)). Entonces, necesitamos volver a integrarnos por partes. (Nota: En su clase de cálculo puede recordar que existe un método tabular para llevar a cabo múltiples aplicaciones de la fórmula. Mostraremos este método en el siguiente ejemplo.)
Aplicamos integración por partes por dejar\(U=x\) y\(d V=\sin x d x\). Esto da\(d U=d x\) y\(V=-\cos x\). Por lo tanto, tenemos
\[ \begin{aligned} \int_{0}^{\pi} x \sin x d x &=-\left.x \cos x\right|_{0} ^{\pi}+\int_{0}^{\pi} \cos x d x \\ &=\pi+\left.\sin x\right|_{0} ^{\pi} \\ &=\pi \end{aligned} \label{A.69} \]
El resultado final es
\[\int_{0}^{\pi} x^{2} \cos x d x=-2 \pi \nonumber \]
Existen otras formas de calcular integrales de este tipo. En primer lugar, está el Método Tabular para realizar la integración por partes. Un segundo método consiste en utilizar la diferenciación de parámetros bajo la integral. Demostraremos esto usando ejemplos.
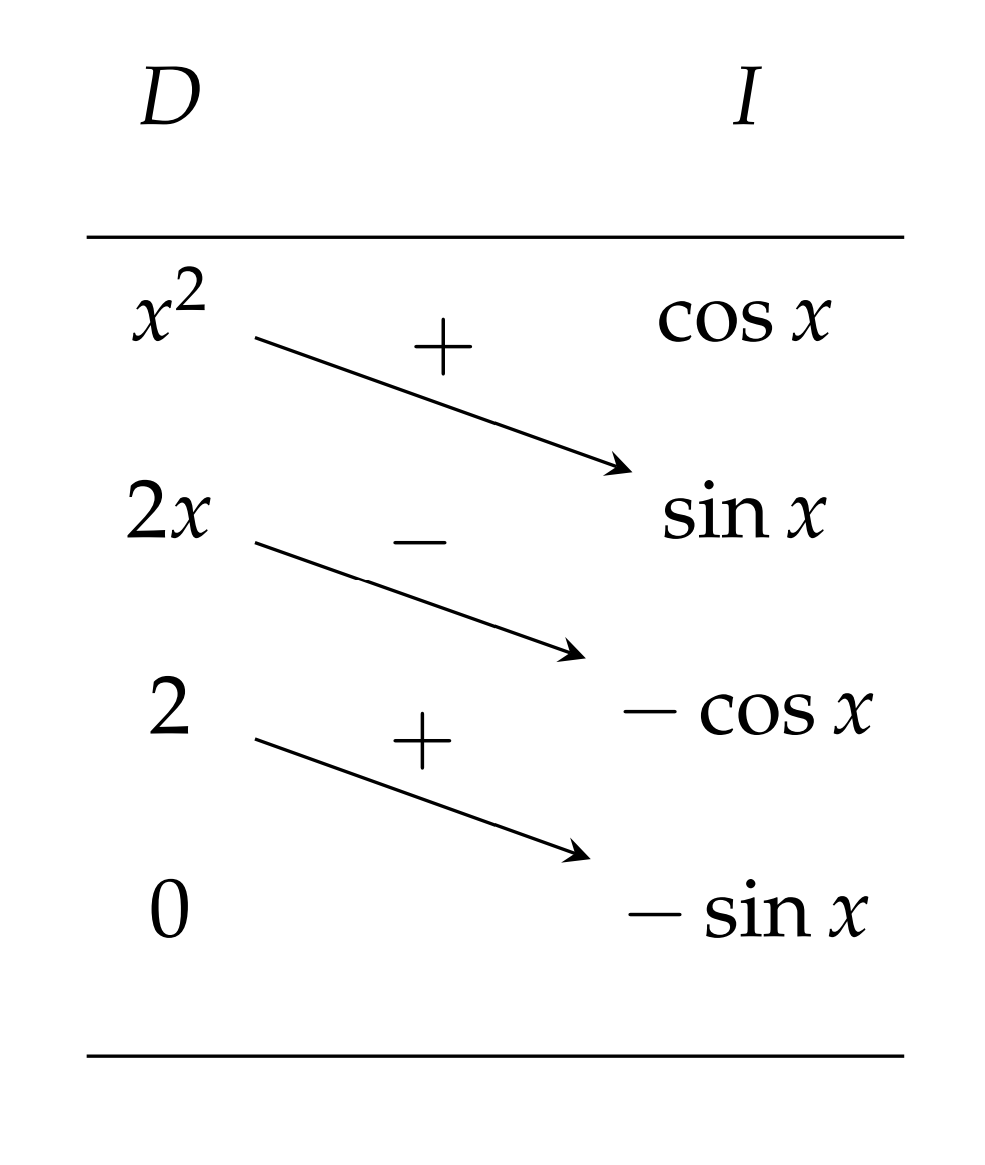
Calcular la integral\(\int_{0}^{\pi} x^{2} \cos x d x\) usando el Método Tabular.
(Usando el Método Tabular). Primero identificamos las dos funciones bajo la integral,\(x^{2}\) y\(\cos x\). Luego escribimos las dos funciones y enumeramos las derivadas e integrales de cada una, respectivamente. Esto se muestra en el Cuadro A.4. Tenga en cuenta que paramos
Primero cuando llegamos a cero en la columna de la izquierda.
A continuación, se dibujan flechas diagonales, como se indica, con signos alternos adjuntos, comenzando por\(+\). La integral indefinida se obtiene entonces sumando los productos de las funciones en los extremos de las flechas junto con los signos en cada flecha:
\[\int x^{2} \cos x d x=x^{2} \sin x+2 x \cos x-2 \sin x+C \nonumber \]
Para encontrar la integral definida, se evalúa la antiderivada en los límites dados.
\[ \begin{aligned} \int_{0}^{\pi} x^{2} \cos x d x &=\left[x^{2} \sin x+2 x \cos x-2 \sin x\right]_{0}^{\pi} \\ &=\left(\pi^{2} \sin \pi+2 \pi \cos \pi-2 \sin \pi\right)-0 \\ &=-2 \pi . \end{aligned} \label{A.70} \]
En realidad, el Método Tabular funciona aunque no aparezca un cero en la columna izquierda. Uno puede llegar lo más lejos posible, y si no aparece un cero, entonces uno solo necesita integrar, si es posible, el producto de las funciones en la última fila, sumando el siguiente signo en la progresión del signo alterno. El siguiente ejemplo muestra cómo funciona esto.
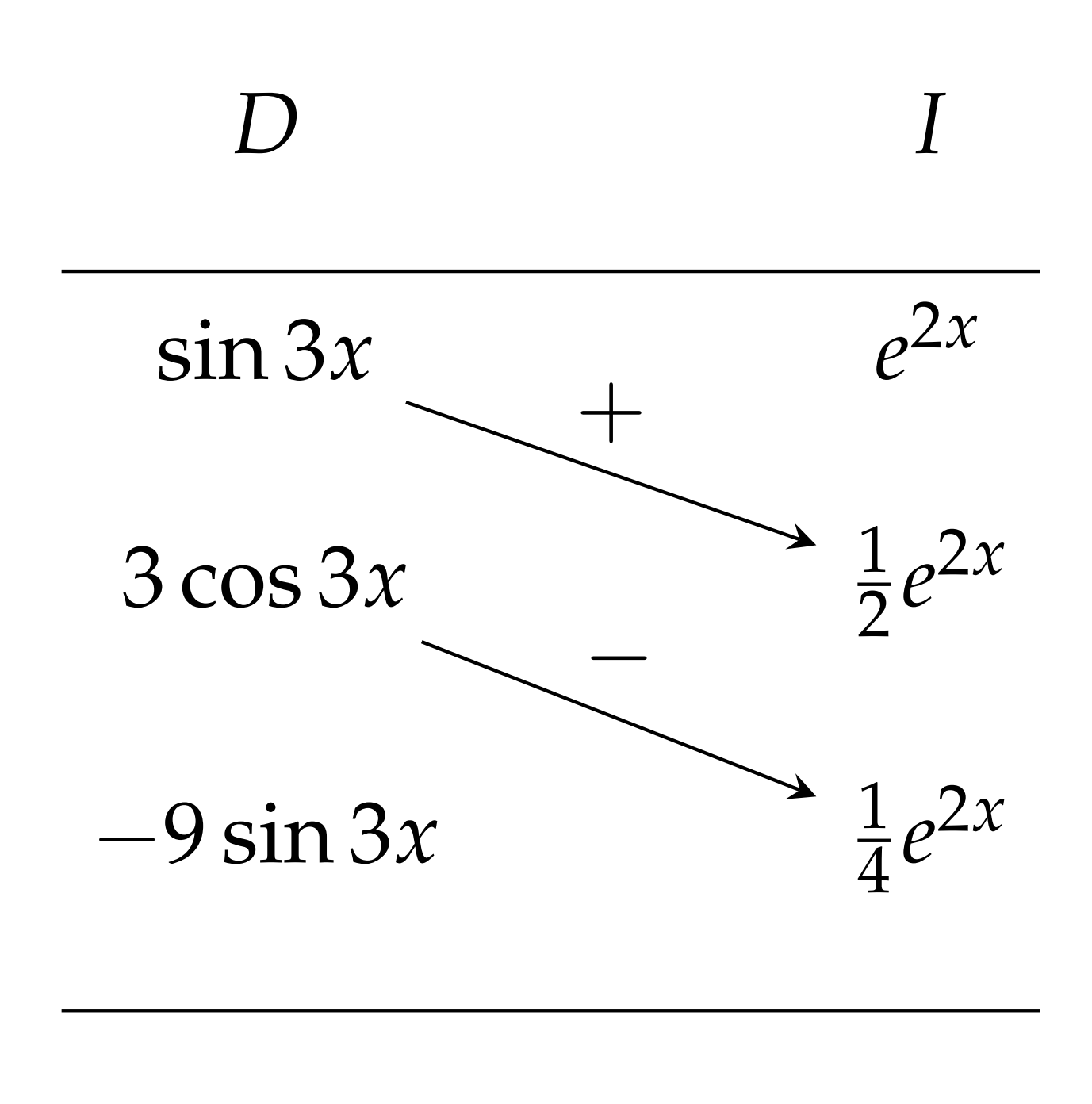
Utilice el Método Tabular para calcular\(\int e^{2 x} \sin 3 x d x\).
Como antes, primero configuramos la tabla como se muestra en la Figura\(\PageIndex{2}\).
Armando las piezas, señalando que los derivados en la columna izquierda nunca desaparecerán, tenemos
\[\int e^{2 x} \sin 3 x d x=\left(\dfrac{1}{2} \sin 3 x-\dfrac{3}{4} \cos 3 x\right) e^{2 x}+\int(-9 \sin 3 x)\left(\dfrac{1}{4} e^{2 x}\right) d x \nonumber \]
La integral de la derecha es un múltiplo de la de la izquierda, así podemos combinarlas,
\[\dfrac{13}{4} \int e^{2 x} \sin 3 x d x=\left(\dfrac{1}{2} \sin 3 x-\dfrac{3}{4} \cos 3 x\right) e^{2 x} \nonumber \]
o
\[\int e^{2 x} \sin 3 x d x=\left(\dfrac{2}{13} \sin 3 x-\dfrac{3}{13} \cos 3 x\right) e^{2 x}\nonumber \]
Diferenciación Bajo la Integral
Diferenciación Bajo el Signo Integral y el truco de Feynman.
Otro método que se puede utilizar para evaluar esta integral es diferenciar bajo el signo integral. Esto se menciona en las memorias de Richard Feynman ¡Seguramente está bromeando, señor Feynman!. En el libro Feynman relata usar este “truco” para poder hacer integrales que sus compañeros del MIT no pudieron hacer. Esto se basa en un teorema que se encuentra en los textos de Cálculo Avanzado. El lector que no esté familiarizado con las derivadas parciales debería ser capaz de comprender su uso en el siguiente ejemplo.
Dejar que las funciones\(f(x, t)\) y\(\dfrac{\partial f(x, t)}{\partial x}\) sean continuas en ambas\(t\)\(x\), y, en la región del\((t, x)\) plano que incluye\(a(x) \leq t \leq b(x), x_{0} \leq x \leq x_{1}\), donde las funciones\(a(x)\) y \(b(x)\)son continuos y tienen derivados continuos para\(x_{0} \leq x \leq x_{1}\). Definiendo
\[F(x) \equiv \int_{a(x)}^{b(x)} f(x, t) d t, \nonumber \]
entonces
\[ \begin{aligned} \dfrac{d F(x)}{d x} &=\left(\dfrac{\partial F}{\partial b}\right) \dfrac{d b}{d x}+\left(\dfrac{\partial F}{\partial a}\right) \dfrac{d a}{d x}+\int_{a(x)}^{b(x)} \dfrac{\partial}{\partial x} f(x, t) d t \\ &=f(x, b(x)) b^{\prime}(x)-f(x, a(x)) a^{\prime}(x)+\int_{a(x)}^{b(x)} \dfrac{\partial}{\partial x} f(x, t) d t \end{aligned} \label{A.71} \]
para\(x_{0} \leq x \leq x_{1}\). Se trata de una versión generalizada del Teorema Fundamental del Cálculo.
En los siguientes ejemplos mostramos cómo podemos usar este teorema para eludir la integración por partes.
Utilizar la diferenciación bajo el signo integral para evaluar\(\int x e^{x} d x\). En primer lugar, considere la integral
\[I(x, a)=\int e^{a x} d x=\dfrac{e^{a x}}{a} \nonumber \]
Entonces,
\[\dfrac{\partial I(x, a)}{\partial a}=\int x e^{a x} d x\nonumber \]
\(\mathrm{SO}\)
\[ \begin{aligned} \int x e^{a x} d x &=\dfrac{\partial I(x, a)}{\partial a} \\ &=\dfrac{\partial}{\partial a}\left(\int e^{a x} d x\right) \\ &=\dfrac{\partial}{\partial a}\left(\dfrac{e^{a x}}{a}\right) \\ &=\left(\dfrac{x}{a}-\dfrac{1}{a^{2}}\right) e^{a x} \end{aligned} \label{A.72} \]
Evaluando este resultado en\(a=1\), tenemos
\[\int x e^{x} d x=(x-1) e^{x} \nonumber \]
El lector puede verificar este resultado empleando los métodos anteriores o simplemente diferenciando el resultado.
Haremos la integral\(\int_{0}^{\pi} x^{2} \cos x d x\) una vez más. En primer lugar, considere la integral
\[ \begin{aligned} I(a) & \equiv \int_{0}^{\pi} \cos a x d x \\ &=\left.\dfrac{\sin a x}{a}\right|_{0} ^{\pi} \\ &=\dfrac{\sin a \pi}{a} \end{aligned} \label{A.73} \]
Diferenciar la integral\(I(a)\) con respecto a\(a\) dos veces da
\[\dfrac{d^{2} I(a)}{d a^{2}}=-\int_{0}^{\pi} x^{2} \cos a x dx \nonumber \]
Evaluación de este resultado en\(a=1\) conduce al resultado deseado. A saber,
\[ \begin{aligned} \int_{0}^{\pi} x^{2} \cos x d x &=-\left.\dfrac{d^{2} I(a)}{d a^{2}}\right|_{a=1} \\ &=-\left.\left.\dfrac{d^{2}}{d a^{2}}\left(\dfrac{\sin a \pi}{a}\right)\right|_{a=1}\right|_{a=1} \\ &\left.=-\left.\dfrac{d}{d a}\left(\dfrac{a \pi \cos a \pi-\sin a \pi}{a^{2}}\right)\right|_{a^{3}}\right)\left.\right|_{a=1} \\ &=-\left(\dfrac{a^{2} \pi^{2} \sin a \pi+2 a \pi \cos a \pi-2 \sin a \pi}{-2 \pi .}\right. \end{aligned} \label{A.75} \]
Integrales trigonométricas
Otros tipos de integrales que verás a menudo son integrales trigonométricas. En particular, integrales que involucran poderes de senos y cosenos. Para los poderes impares, una simple sustitución convertirá las integrales en simples potencias.
Por ejemplo, considere
\[\int \cos ^{3} x d x \nonumber \]
Solución
Esto se puede reescribir como
\[\int \cos ^{3} x d x=\int \cos ^{2} x \cos x d x \nonumber \]
Integración de potencias impares de seno y coseno. Vamos\(u=\sin x\). Entonces,\(d u=\cos x d x\). Desde entonces\(\cos ^{2} x=1-\sin ^2 x\), tenemos
\[ \begin{aligned} \int \cos ^{3} x d x&=\int \cos ^{2} x \cos x d x \\ &=\int\left(1-u^{2}\right) d u \\ &=u-\dfrac{1}{3} u^{3}+C \\ &=\sin x-\dfrac{1}{3} \sin ^{3} x+C . \end{aligned} \label{A.76} \]
Un chequeo rápido confirma la respuesta:
\[ \begin{aligned} \dfrac{d}{d x}\left(\sin x-\dfrac{1}{3} \sin ^{3} x+C\right) &=\cos x-\sin ^{2} x \cos x \\ &=\cos x\left(1-\sin ^{2} x\right) \\ &=\cos ^{3} x \end{aligned} \label{A.77} \]
Incluso los poderes de los senos y los cosenos son un poco más complicados, pero factibles. En estos casos necesitamos las fórmulas de medio ángulo (A.24) - (A.25).
(Integración de potencias pares de seno y coseno).
Como ejemplo, vamos a calcular
\[\int_{0}^{2 \pi} \cos ^{2} x d x \nonumber \]
.
Solución
Sustituyendo la fórmula de medio ángulo por\(\cos ^{2} x\), tenemos
\[ \begin{aligned} \int_{0}^{2 \pi} \cos ^{2} x d x &=\dfrac{1}{2} \int_{0}^{2 \pi}(1+\cos 2 x) d x \\ &=\dfrac{1}{2}\left(x-\dfrac{1}{2} \sin 2 x\right)_{0}^{2 \pi} \\ &=\pi \end{aligned} \label{A.78} \]
Observamos que este resultado aparece a menudo en la física. Al observar los promedios cuadráticos medios de las ondas sinusoidales, se necesita el promedio del cuadrado de senos y cosenos. Recordemos que el promedio de una función en el intervalo\([a, b]\) se da como
\[f_{\text {ave }}=\dfrac{1}{b-a} \int_{a}^{b} f(x) d x \nonumber \]
Entonces, el promedio de\(\cos ^{2} x\) más de un periodo es
\[\dfrac{1}{2 \pi} \int_{0}^{2 \pi} \cos ^{2} x d x=\dfrac{1}{2} . \nonumber \]
La raíz media cuadrada se encuentra entonces tomando la raíz cuadrada,\(\dfrac{1}{\sqrt{2}}\).
Recordemos que los promedios RMS se refieren al promedio cuadrático medio raíz. Esto se calcula calculando primero el promedio, o media, del cuadrado de alguna cantidad. Entonces uno toma la raíz cuadrada. Ejemplos típicos son el voltaje RMS, la corriente RMS y la energía promedio en una onda electromagnética. Las corrientes de CA oscilan tan rápido que el valor medido es el voltaje RMS.
Sustitución de funciones trigonométricas
Otra clase de integrales típicamente estudiadas en el cálculo son las que involucran las formas\(\sqrt{1-x^2}\),\(\sqrt{1 + x^2 }\), o\(\sqrt{x^2 − 1\). Estos pueden simplificarse mediante el uso de sustituciones trigonométricas. La idea es combinar los dos términos bajo el radical en un término usando identidades trigonométricas. Consideraremos algunos ejemplos típicos.
Evaluar\(\int \sqrt{1-x^2} dx\).
Solución
Ya que\(1-\sin ^{2} \theta=\cos ^{2} \theta\), realizamos la sustitución sinusoidal
\[x=\sin \theta, \quad d x=\cos \theta d \theta\nonumber \]
En cualquiera de estos cómputos se tiene que prestar mucha atención a la simplificación del radical. Esto se debe a que
\[\sqrt{x^2} =|x|. \nonumber \]
Por ejemplo,\(\sqrt{(-5)^{2}}=\sqrt{25}=5\). Para\(x=\sin \theta, \) uno normalmente especifica el dominio\(-\pi / 2 \leq \theta \leq \pi / 2.\) En este dominio tenemos\(|\cos \theta|=\cos \theta\).
Entonces,
\[ \begin{aligned} \int \sqrt{1-x^{2}} d x &=\int \sqrt{1-\sin ^{2} \theta} \cos \theta d \theta \\ &=\int \cos ^{2} \theta d \theta. \end{aligned} \label{A.81} \]
Usando el último ejemplo, tenemos
\[\int \sqrt{1-x^{2}} d x=\dfrac{1}{2}\left(\theta-\dfrac{1}{2} \sin 2 \theta\right)+C .\nonumber \]
Sin embargo, necesitamos escribir la respuesta en términos de\(x\). Hacemos esto usando primero la fórmula de doble ángulo para\(\sin 2 \theta\) y\(\cos \theta=\sqrt{1-x^{2}}\) para obtener
\[\int \sqrt{1-x^{2}} d x=\dfrac{1}{2}\left(\sin ^{-1} x-x \sqrt{1-x^{2}}\right)+C .\nonumber \]
Sustituciones trigonométricas similares resultan para los integrandos que involucran\(\sqrt{1+x^{2}}\) y\(\sqrt{x^{2}-1}\). Las sustituciones se resumen en la Tabla A.6. La simplificación de la forma dada se obtiene a partir de identidades trigonométricas. Esto también se puede lograr haciendo referencia a los triángulos rectos mostrados en la Figura\(\PageIndex{3}\).
| Formulario | Sustitución | Diferencial |
|---|---|---|
| \(\sqrt{a^{2}-x^{2}}\) | \(x=a \sin \theta\) | \(d x=a \cos \theta d \theta\) |
| \(\sqrt{a^{2}+x^{2}}\) | \(x=a \tan \theta\) | \(d x=a \sec ^{2} \theta d \theta\) |
| \(\sqrt{x^{2}-a^{2}}\) | \(x=a \sec \theta\) | \(d x=a \sec \theta \tan \theta d \theta\) |
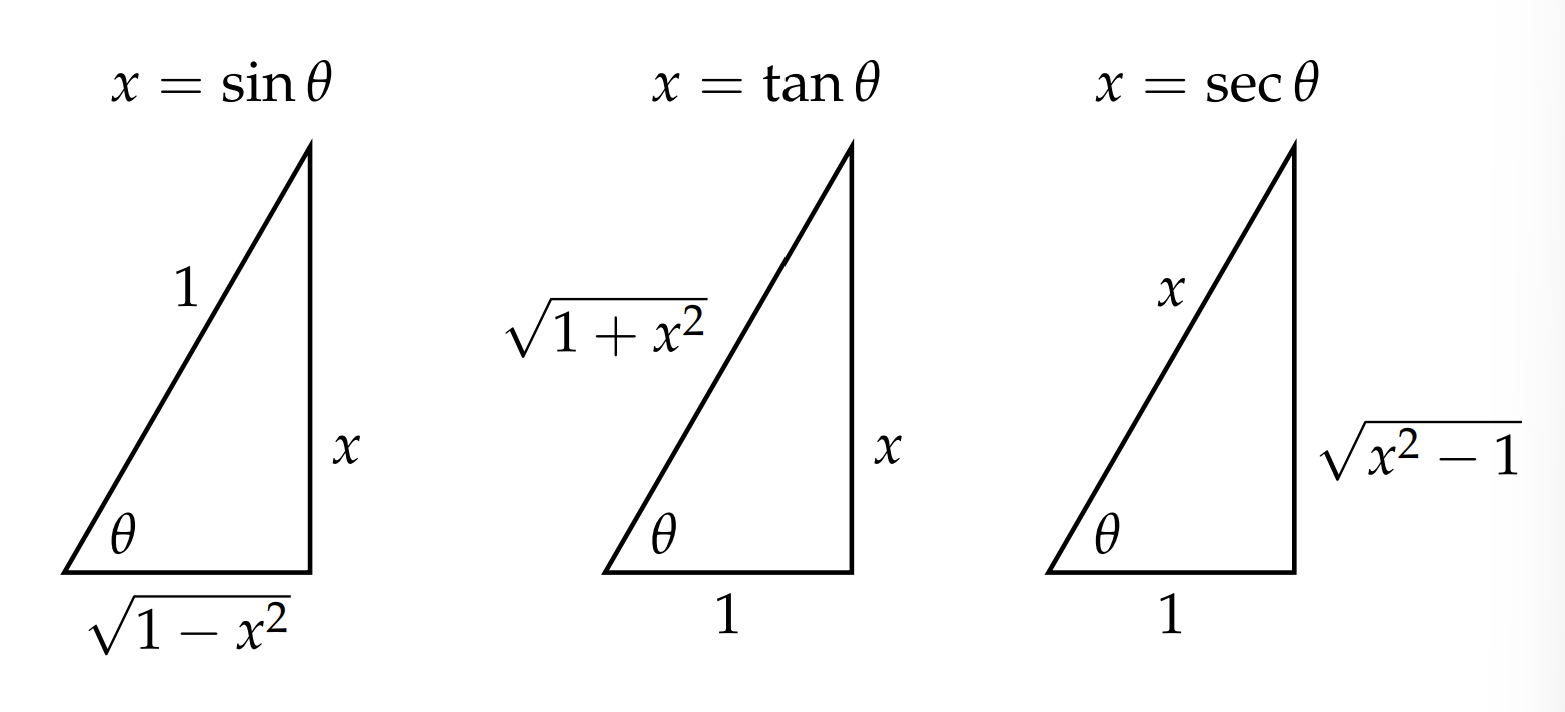
Evaluar\(\int_{0}^{2} \sqrt{x^{2}+4} d x\).
Solución
Vamos\(x=2 \tan \theta\). Entonces,\(d x=2 \sec ^{2} \theta d \theta\) y
\[\sqrt{x^{2}+4}=\sqrt{4 \tan ^{2} \theta+4}=2 \sec \theta \nonumber \]
Entonces, la integral se convierte
\[\int_{0}^{2} \sqrt{x^{2}+4} d x=4 \int_{0}^{\pi / 4} \sec ^{3} \theta d \theta\nonumber \]
Uno tiene que recordar, o mirar hacia arriba,
\[\int \sec ^{3} \theta d \theta=\dfrac{1}{2}(\tan \theta \sec \theta+\ln |\sec \theta+\tan \theta|)+C. \nonumber \]
Esto da
\[ \begin{aligned} \int_{0}^{2} \sqrt{x^{2}+4} d x &=2[\tan \theta \sec \theta+\ln |\sec \theta+\tan \theta|]_{0}^{\pi / 4} \\ &=2(\sqrt{2}+\ln |\sqrt{2}+1|-(0+\ln (1))) \\ &=2(\sqrt{2}+\ln (\sqrt{2}+1)) \end{aligned} \label{A.82} \]
Evaluar\(\int \dfrac{d x}{\sqrt{x^{2}-1}}, x \geq 1\).
Solución
En este caso se necesita la sustitución secante. Esto rinde
\[ \begin{aligned} \int \dfrac{d x}{\sqrt{x^{2}-1}} &=\int \dfrac{\sec \theta \tan \theta d \theta}{\sqrt{\sec ^{2} \theta-1}} \\ &=\int \dfrac{\sec \theta \tan \theta d \theta}{\tan \theta} \\ &=\int \sec \theta d \theta \\ &=\ln (\sec \theta+\tan \theta)+C \\ &=\ln \left(x+\sqrt{x^{2}-1}\right)+C . \end{aligned} \nonumber \]
Evaluar\(\int \dfrac{d x}{x \sqrt{x^{2}-1}}, x \geq 1\).
Nuevamente podemos usar una sustitución secante. Esto rinde
\[ \begin{aligned} \int \dfrac{d x}{x \sqrt{x^{2}-1}} &=\int \dfrac{\sec \theta \tan \theta d \theta}{\sec \theta \sqrt{\sec ^{2} \theta-1}} \\ &=\int \dfrac{\sec \theta \tan \theta}{\sec \theta \tan \theta} d \theta \\ &=\int d \theta=\theta+C=\sec ^{-1} x+C . \end{aligned} \nonumber \]
Sustitución de función hiperbólica
A pesar de que la sustitución trigonométrica juega un papel en el programa de cálculo, los estudiantes suelen ver la sustitución de funciones hiperbólicas utilizada en los cursos de física. La razón podría ser porque la sustitución de funciones hiperbólicas a veces es más simple. La idea es la misma que para la sustitución trigonométrica. Utilizamos una identidad para simplificar lo radical.
Evaluar\(\int_{0}^{2} \sqrt{x^{2}+4} d x\) usando la sustitución\(x=2 \sinh u\).
Solución
Ya que\(x=2 \sinh u\), tenemos\(d x=2 \cosh u d u .\) También, podemos usar la identidad\(\cosh ^{2} u-\sinh ^{2} u=1\) para reescribir
\[\sqrt{x^{2}+4}=\sqrt{4 \sinh ^{2} u+4}=2 \cosh u\nonumber \]
La integral puede evaluarse ahora usando estas sustituciones y algunas identidades de funciones hiperbólicas,
\[ \begin{aligned} \int_{0}^{2} \sqrt{x^{2}+4} d x &=4 \int_{0}^{\sinh ^{-1} 1} \cosh ^{2} u d u \\ &=2 \int_{0}^{\sinh ^{-1} 1}(1+\cosh 2 u) d u \\ &=2\left[u+\dfrac{1}{2} \sinh 2 u\right]_{0}^{\sinh ^{-1} 1} \\ &=2[u+\sinh u \cosh u]_{0}^{\sinh ^{-1} 1} \\ &=2\left(\sinh ^{-1} 1+\sqrt{2}\right) \end{aligned} \label{A.85} \]
En el Ejemplo A.17 se utilizó una sustitución trigonométrica y se encontró
\[\int_{0}^{2} \sqrt{x^{2}+4}=2(\sqrt{2}+\ln (\sqrt{2}+1)) \nonumber \]
Este es el mismo resultado desde entonces\(\sinh ^{-1} 1=\ln (1+\sqrt{2})\).
Evaluar\(\int \dfrac{d x}{\sqrt{x^{2}-1}}\) para\(x \geq 1\) usar sustitución de función hiperbólica.
Solución
Esta integral se evaluó en Ejemplo\(\PageIndex{16}\) usando la sustitución trigonométrica\(x=\sec \theta\) y la integral resultante de\(\sec \theta\) tuvo que ser recordada. Aquí usaremos la sustitución
\(x=\cosh u, \quad d x=\sinh u d u, \quad \sqrt{x^{2}-1}=\sqrt{\cosh ^{2} u-1}=\sinh u\)
Entonces,
\[ \begin{aligned} \int \dfrac{d x}{\sqrt{x^{2}-1}} &=\int \dfrac{\sinh u d u}{\sinh u} \\ &=\int d u=u+C \\ &=\cosh ^{-1} x+C \\ &=\dfrac{1}{2} \ln \left(x+\sqrt{x^{2}-1}\right)+C, \quad x \geq 1 \end{aligned} \label{A.86} \]
Este es el mismo resultado que habíamos obtenido anteriormente, pero esta derivación fue un poco más limpia.
Además, podemos extender este resultado a los valores\(x \leq-1\) dejando\(x=\) - cosh\(u\). Esto da
\[\int \dfrac{d x}{\sqrt{x^{2}-1}}=\dfrac{1}{2} \ln \left(x+\sqrt{x^{2}-1}\right)+C, \quad x \leq-1 \nonumber \]
Combinando estos resultados, hemos demostrado
\[\int \dfrac{d x}{\sqrt{x^{2}-1}}=\dfrac{1}{2} \ln \left(|x|+\sqrt{x^{2}-1}\right)+C, \quad x^{2} \geq 1 \nonumber \]
Hemos visto en el último ejemplo que el uso de la sustitución de función hiperbólica nos permite eludir integrando la función secante en Ejemplo\(\PageIndex{16}\) cuando se utilizan sustituciones trigonométricas. De hecho, podemos usar sustituciones hiperbólicas para evaluar integrales de poderes de secantes. Comparando Ejemplo\(\PageIndex{16}\) y Ejemplo\(\PageIndex{18}\), consideramos la transformación\(\sec \theta=\cosh u\). La relación entre diferenciales se encuentra por diferenciación, dando
\[\sec \theta \tan \theta d \theta=\sinh u d u\nonumber \]
Desde
\[\tanh ^{2} \theta=\sec ^{2} \theta-1\nonumber \]
tenemos\(\tan \theta=\sinh u\), por lo tanto
\[d \theta=\dfrac{d u}{\cosh u} \nonumber \]
En el siguiente ejemplo mostramos lo útil que es esta transformación.
(Evaluación de\(\int \sec \theta d \theta\)).
Evaluar\(\int \sec \theta d \theta\) mediante sustitución de función hiperbólica.
Solución
De la discusión en el último párrafo, tenemos
\[ \begin{aligned} \int \sec \theta d \theta &=\int d u \\ &=u+C \\ &=\cosh ^{-1}(\sec \theta)+C \end{aligned} \label{A.87} \]
Podemos expresar este resultado en la forma habitual utilizando la forma logarítmica del coseno hiperbólico inverso,
\[\cosh ^{-1} x=\ln \left(x+\sqrt{x^{2}-1}\right) \nonumber \]
El resultado es
\[\int \sec \theta d \theta=\ln (\sec \theta+\tan \theta)\nonumber \]
Este ejemplo fue bastante simple usando la transformación\(\sec \theta=\cosh u\). Otra integral común que surge a menudo son las integraciones de\(\sec ^{3} \theta\). En una clase típica de cálculo esta integral se evalúa mediante integración por partes. Sin embargo. eso lleva a una manipulación complicada que da un poco de miedo la primera vez que se encuentra (y probablemente en varios encuentros más). En el siguiente ejemplo, mostraremos cómo la sustitución de funciones hiperbólicas es más sencilla.
(Evaluación de\(\int \sec ^{3} \theta d \theta\)).
Evaluar\(\int \sec ^{3} \theta d \theta\) mediante sustitución de función hiperbólica.
Solución
Primero, consideramos la transformación\(\sec \theta=\cosh u\) con\(d \theta=\)\(\dfrac{d u}{\cosh u}\). Entonces,
\[\int \sec ^{3} \theta d \theta=\int \dfrac{d u}{\cosh u}\nonumber \]
Esta integral se realizó en el Ejemplo A.7, lo que llevó a
\[\int \sec ^{3} \theta d \theta=2 \tan ^{-1} e^{u}+C \nonumber \]
Si bien es correcto, esta no es la forma que se suele encontrar. En cambio, hacemos la transformación ligeramente diferente\(\tan \theta=\sinh u\). Ya que\(\sec ^{2} \theta=1+\tan ^{2} \theta\), encontramos\(\sec \theta=\cosh u .\) como antes, encontramos
\[d \theta=\dfrac{d u}{\cosh u} \nonumber \]
Usando esta transformación y varias identidades, la integral se convierte
\[ \begin{aligned} \int \sec ^{3} \theta d \theta &=\int \cosh ^{2} u d u \\ &=\dfrac{1}{2} \int(1+\cosh 2 u) d u \\ &=\dfrac{1}{2}\left(u+\dfrac{1}{2} \sinh 2 u\right) \\ &=\dfrac{1}{2}(u+\sinh u \cosh u) \\ &=\dfrac{1}{2}\left(\cosh ^{-1}(\sec \theta)+\tan \theta \sec \theta\right) \\ &=\dfrac{1}{2}(\sec \theta \tan \theta+\ln (\sec \theta+\tan \theta)) \end{aligned} \label{A.88} \]
Existen muchos otros métodos de integración, algunos de los cuales visitaremos en otras partes del libro, como la descomposición parcial de fracciones y la integración numérica. Otro tema que volveremos a visitar es la serie power.


