7.4: Funciones de Bessel
- Page ID
- 118901
Otra ecuación diferencial importante que surge en muchas aplicaciones de la física es
\[x^{2} y^{\prime \prime}+x y^{\prime}+\left(x^{2}-p^{2}\right) y=0 . \label{7.37} \]
Esta ecuación se pone fácilmente en forma autoadjoint como
\[\left(x y^{\prime}\right)^{\prime}+\left(x-\dfrac{p^{2}}{x}\right) y=0 . \label{7.38} \]
Esta ecuación se resolvió en el primer curso sobre ecuaciones diferenciales utilizando métodos de series de potencia, es decir, utilizando el Método Frobenius. Uno asume una solución en serie de la forma
\[y(x)=\sum_{n=0}^{\infty} a_{n} x^{n+s}, \nonumber \]
y se busca valores permitidos de la constante\(s\) y una relación de recursión para los coeficientes,\(a_{n}\). Uno encuentra eso\(s=\pm p\) y
\[a_{n}=-\dfrac{a_{n-2}}{(n+s)^{2}-p^{2}}, \quad n \geq 2 . \nonumber \]
Una solución de la ecuación diferencial es la función de Bessel del primer tipo de orden\(p\), dada como
\[y(x)=J_{p}(x)=\sum_{n=0}^{\infty} \dfrac{(-1)^{n}}{\Gamma(n+1) \Gamma(n+p+1)}\left(\dfrac{x}{2}\right)^{2 n+p} . \label{7.39} \]
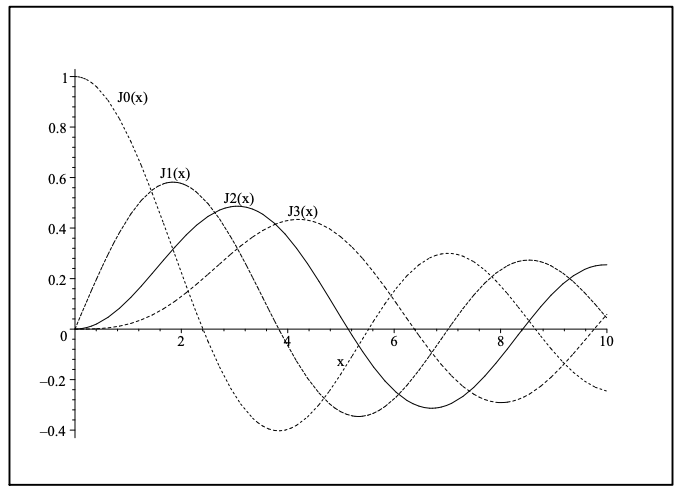
En la Figura 7.7 se muestran las primeras funciones de Bessel del primer tipo de orden entero. Tenga en cuenta que estas funciones pueden describirse como funciones oscilatorias en descomposición.
Se obtiene una segunda solución linealmente independiente para\(p\) no un número entero como\(J_{-p}(x)\). Sin embargo, para\(p\) un entero, el\(\Gamma(n+p+1)\) factor conduce a evaluaciones de la función Gamma en cero, o enteros negativos, cuando\(p\) es negativo. Por lo tanto, la serie anterior no se define en estos casos.
Otro método para obtener una segunda solución linealmente independiente es a través de una combinación lineal de\(J_{p}(x)\) y\(J_{-p}(x)\) como
\[N_{p}(x)=Y_{p}(x)=\dfrac{\cos \pi p J_{p}(x)-J_{-p}(x)}{\sin \pi p} \label{7.40} \]
Estas funciones se llaman las funciones de Neumann, o funciones de Bessel del segundo tipo de orden\(p\).
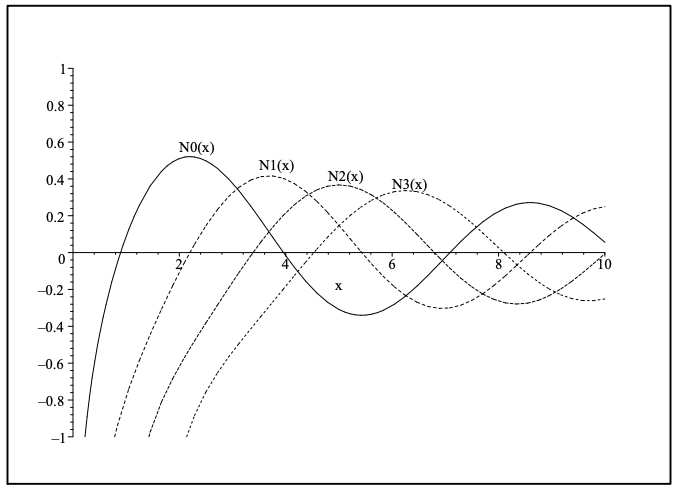
En la Figura 7.8 mostramos las primeras funciones de Bessel del segundo tipo de orden entero. Tenga en cuenta que estas funciones también son funciones oscilatorias en descomposición. Sin embargo, son singulares en\(x=0\).
En muchas aplicaciones, estas funciones no satisfacen la condición de límite en la que se desea una solución limitada\(x=0\). Por ejemplo, un problema estándar es describir las oscilaciones de un tambor circular. Para este problema se resuelve la ecuación de onda utilizando la separación de variables en coordenadas cilíndricas. La\(r\) ecuación conduce a una ecuación de Bessel. Las soluciones de la función de Bessel describen la parte radial de la solución y no se espera una solución singular en el centro del tambor. La amplitud de la oscilación debe permanecer finita. Así, solo se pueden usar funciones de Bessel del primer tipo.
Las funciones de Bessel satisfacen una variedad de propiedades, que solo enumeraremos en este momento para funciones de Bessel de primer tipo.
\[\dfrac{d}{d x}\left[x^{p} J_{p}(x)\right]=x^{p} J_{p-1}(x) \label{7.41} \]
\[\dfrac{d}{d x}\left[x^{-p} J_{p}(x)\right]=-x^{-p} J_{p+1}(x) \label{7.42} \]
\[J_{p-1}(x)+J_{p+1}(x)=\dfrac{2 p}{x} J_{p}(x) \label{7.43} \]
\[J_{p-1}(x)-J_{p+1}(x)=2 J_{p}^{\prime}(x) \label{7.44} \]
\[\int_{0}^{a} x J_{p}\left(j_{p n} \dfrac{x}{a}\right) J_{p}\left(j_{p m} \dfrac{x}{a}\right) d x=\dfrac{a^{2}}{2}\left[J_{p+1}\left(j_{p n}\right)\right]^{2} \delta_{n, m} \label{7.45} \]
donde\(j_{p n}\) está la raíz\(n\) th de\(J_{p}(x), J_{p}\left(j_{p n}\right)=0, n=1,2, \ldots\) Una lista de algunas de estas raíces se proporcionan en la Tabla 7.4.
\ (\ begin {array} {c|c|c|c|c|c|c}
n & p=0 & p=1 & p=2 & p=3 & p=4 & p=5\
\ hline 1 & 2.405 & 3.832 & 5.135 & 6.379 & 7.586 & 8.780\\
2 & 5.520 & 7.016 & 8.147 & 9.760 & 11.064 & 12.339\\
3 & 8.654 & 10.173 & 11.620 & 13.017 & 14.373 & 15.700\\
4 & 11.792 & 13.323 & 14.796 & 16.224 & 17.616 & 18.982\\
5 & 14.931 & 16.470 & 17.960 & 19.410 & 20.827 & 22.220\\
6 & 18.071 & 19.616 & 21.117 & 22.583 & 24.018 & 25.431\\
7 & 21.212 & 22.760 & 24.270 & 25.749 & 27.200 & 28.628\\
8 & 24.353 & 25.903 & 27.421 & 28.909 & 30.371 & 31.813\\
9 & 27.494 & 29.047 & 30.571 y 32.050 y 33.512 y 34.983
\ end {array}\)
Cuadro 7.4. Los ceros de las funciones de Bessel
Función generadora
\[e^{x\left(t-\dfrac{1}{t}\right) / 2}=\sum_{n=-\infty}^{\infty} J_{n}(x) t^{n}, \quad x>0, t \neq 0 . \label{7.46} \]
Representación Integral
\[J_{n}(x)=\dfrac{1}{\pi} \int_{0}^{\pi} \cos (x \sin \theta-n \theta) d \theta, \quad x>0, n \in \mathrm{Z} . \label{7.47} \]
Serie Fourier-Bessel
Dado que las funciones de Bessel son un conjunto ortogonal de funciones propias de un problema de Sturm-Liouville, podemos expandir funciones integrables cuadradas en esta base. De hecho, el problema del valor propio se da en la forma
\[x^{2} y^{\prime \prime}+x y^{\prime}+\left(\lambda x^{2}-p^{2}\right) y=0 . \label{7.48} \]
Las soluciones son entonces de la forma\(J_{p}(\sqrt{\lambda} x)\), como se puede demostrar haciendo la sustitución\(t=\sqrt{\lambda} x\) en la ecuación diferencial.
Además, se puede resolver la ecuación diferencial en un dominio finito,\([0, a]\), con las condiciones límite:\(y(x)\) está delimitado en\(x=0\) y\(y(a)= 0\). Se puede demostrar que\(J_{p}\left(j_{p n} \dfrac{x}{a}\right)\) es una base de funciones propias y la expansión resultante de la serie Fourier-Bessel de\(f(x)\) defined on\(x \in[0, a]\) es
\[f(x)=\sum_{n=1}^{\infty} c_{n} J_{p}\left(j_{p n} \dfrac{x}{a}\right) \label{7.49} \]
donde se encuentran los coeficientes de Fourier-Bessel usando la relación de ortogonalidad como
\[c_{n}=\dfrac{2}{a^{2}\left[J_{p+1}\left(j_{p n}\right)\right]^{2}} \int_{0}^{a} x f(x) J_{p}\left(j_{p n} \dfrac{x}{a}\right) d x . \label{7.50} \]
Ejemplo 7.8. Ampliar\(f(x)=1\) para\(0 \leq x \leq 1\) en una serie de Fourier-Bessel del formulario
\[f(x)=\sum_{n=1}^{\infty} c_{n} J_{0}\left(j_{0 n} x\right) \nonumber \]
Solo necesitamos calcular los coeficientes de Fourier-Bessel en la Ecuación (7.50):
\[c_{n}=\dfrac{2}{\left[J_{1}\left(j_{0 n}\right)\right]^{2}} \int_{0}^{1} x J_{0}\left(j_{0 n} x\right) d x . \label{7.51} \]
De la Ecuación (7.41) tenemos
\ [\ comenzar {alineado}
\ int_ {0} ^ {1} x J_ {0}\ izquierda (j_ {0 n} x\ derecha) d x &=\ dfrac {1} {j_ {0 n} ^ {2}}\ int_ {0} ^ {j_ {0 n}} y J_ {0} (y) d y\\
&=\ dfrac {1} {j_ {0 n} ^ {2}}\ int_ {0} ^ {j_ {0 n}}\ dfrac {d} {d y}\ izquierda [y J_ {1} (y)\ derecha] d y\\
&=\ dfrac {1} {j_ {0 n} ^ {2}}\ izquierda [y J_ {1} (y)\ derecha] _ {0} ^ {j_ {0 n}}\\
&=\ dfrac {1} {j_ {0 n}} J_ {1}\ izquierda (j_ {0 n}\ derecha)
\ final {alineado}\ etiqueta {7.52}\]
Como resultado, hemos encontrado que la expansión deseada de Fourier-Bessel es
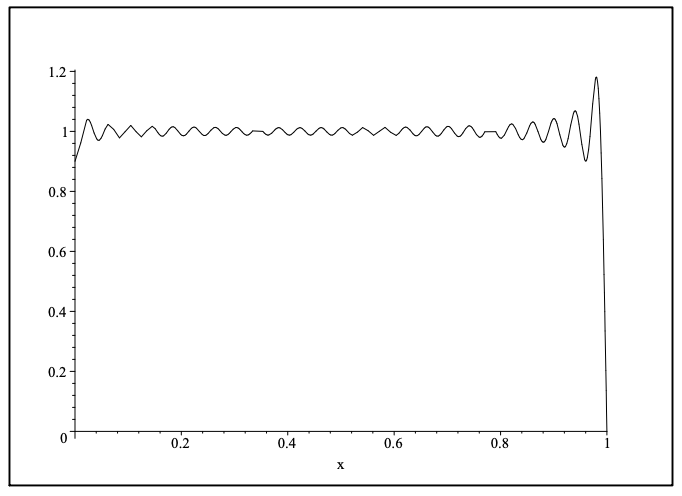
\[1=2 \sum_{n=1}^{\infty} \dfrac{J_{0}\left(j_{0 n} x\right)}{j_{0 n} J_{1}\left(j_{0 n}\right)}, \quad 0<x<1 \label{7.53} \]
En la Figura 7.9 se muestra la suma parcial de los primeros cincuenta términos de esta serie. Vemos que hay una convergencia lenta debido al fenómeno de Gibbs'. Nota: Como referencia, las sumas parciales de la serie Fourier-Bessel se computaron en Maple usando el siguiente código:
2*sum(BesselJ(0,BesselJZeros(0,n)*x) /(BesselJZeros(0,n)*BesselJ(1,BesselJZeros(0,n))),n=1..50)