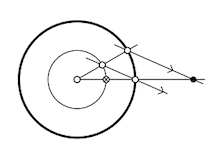
10.1: Inversión
- Page ID
- 114447
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dejar\(\Omega\) ser el círculo con centro\(O\) y radio\(r\). La inversión de un punto\(P\) en\(\Omega\) es el punto\(P' \in [OP)\) tal que
\(OP \cdot OP' = r^2.\)
En este caso el círculo se\(\Omega\) llamará el círculo de inversión y su centro\(O\) se llamará el centro de inversión.
El inverso de\(O\) es indefinido.
Tenga en cuenta que si\(P\)\(P'\) está dentro\(\Omega\), entonces está afuera y al revés. Además,\(P = P'\) si y sólo si\(P \in \Omega\).
Tenga en cuenta que los mapas de inversión se\(P'\) remontan a\(P\).
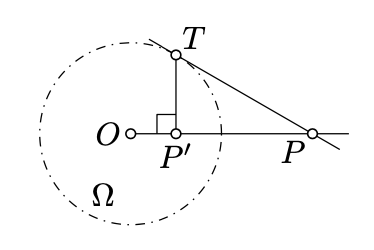
Dejar\(\Omega\) ser un círculo centrado en\(O\). Supongamos que una línea\((PT)\) es tangente a\(\Omega\) at\(T\). Deja\(P'\) ser el punto del pie de\(T\) on\((OP)\).
Demostrar que\(P'\) es la inversa de\(P\) in\(\Omega\).
- Pista
-
Por Lemma 5.6.2,\(\angle OTP'\) tiene razón. Por lo tanto,\(\triangle OPT \sim \triangle OTP'\) y en particular\(OP \cdot OP' = OT^2\) y de ahí el resultado.
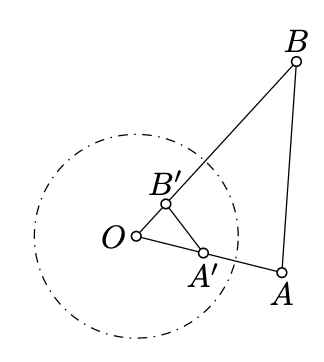
Dejar\(\Gamma\) ser un círculo con el centro\(O\). Asumir\(A'\) y\(B'\) son los inversos de\(A\) y\(B\) en\(\Gamma\). Entonces
\(\triangle OAB \sim \triangle OB'A'.\)
Además
\[\begin{array} {rcl} {\measuredangle AOB} & \equiv & {-\measuredangle B'OA',} \\ {\measuredangle OBA} & \equiv & {-\measuredangle OA'B',} \\ {\measuredangle BAO} & \equiv & {-\measuredangle A'B'O.} \end{array}\]
- Prueba
-
Dejar\(r\) ser el radio del círculo de la inversión.
Por la definición de inversión,
\(OA \cdot OA' = OB \cdot OB' = r^2.\)
Por lo tanto,
\(\dfrac{OA}{OB'} = \dfrac{OB}{OA'}.\)
Claramente,
\(\measuredangle AOB = \measuredangle A'OB' \equiv -\measuredangle B'OA'.\)
De SAS, obtenemos eso
\(\triangle OAB \sim \triangle OB'A'.\)
Aplicando el Teorema 3.3.1 y 10.1.2, obtenemos 10.1.1.
Dejar\(P'\) ser la inversa de\(P\) en el círculo\(\Gamma\). Asumir eso\(P \ne P'\). Demostrar que el valor\(\dfrac{PX}{P'X}\) es el mismo para todos\(X \in \Gamma\).
También se sostiene lo contrario al ejercicio anterior. Es decir, dado un número real positivo\(k \ne 1\) y dos puntos distintos\(P\) y\(P'\) el locus de puntos\(X\) tal que\(\dfrac{PX}{P'X} = k\) forma un círculo que se llama círculo apolónico. En este caso\(P'\) es inverso de\(P\) en el círculo apolónico.
- Pista
-
Supongamos que\(O\) denota el centro de\(\Gamma\). Supongamos que\(X, Y \in \Gamma\); en particular,\(OX = OY\).
Tenga en cuenta que la inversión envía\(X\) y\(Y\) a sí mismos. Por Lemma\(\PageIndex{1}\),
\(\triangle OPX \sim \triangle OXP'\)y\(\triangle OPY \sim \triangle OYP'\).
Por lo tanto,\(\dfrac{PX}{P'X} = \dfrac{OP}{OX} = \dfrac{OP}{OY} = \dfrac{PY}{P'Y}\) y de ahí el resultado.
Dejemos\(A',B'\), y\(C'\) sean las imágenes de\(A,B\), y\(C\) bajo la inversión en el cincírculo de\(\triangle ABC\). Demostrar que el incenter de\(\triangle ABC\) es el ortocentro de\(\triangle A'B'C'\).
- Pista
-
Por Lemma\(\PageIndex{1}\),
\(\measuredangle IA'B' \equiv -\measuredangle IBA\),\(\measuredangle IB'C' \equiv -\measuredangle ICB\),\(\measuredangle IC'A' \equiv -\measuredangle IAC\),
\(\measuredangle IB'A' \equiv -\measuredangle IAB\),\(\measuredangle IC'B' \equiv -\measuredangle IBC\),\(\measuredangle IA'C' \equiv -\measuredangle ICA\).Queda por aplicar el teorema sobre la suma de ángulos de triángulo (Teorema 7.4.1) para mostrar eso\((A'I) \perp (B'C')\),\((B'I) \perp (C'A')\) y\((C'I) \perp (B'A')\).
Hacer una construcción de regla y brújula de la inversa de un punto dado en un círculo dado.
- Pista
-
Adivina la construcción del diagrama (las dos líneas que no se intersectan en el diagrama son paralelas).
