10.5: Círculos perpendiculares

Última actualización
Guardar como PDF

Page ID: 114454

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Asumir dos círculos$\Gamma$ e$\Omega$ intersectar en dos puntos$X$ y$Y$. Dejar$\ell$ y$m$ ser las líneas tangentes en$X$ a$\Gamma$ y$\Omega$ respectivamente. Análogamente,$\ell'$ y$m'$ ser las líneas tangentes en$Y$ a$\Gamma$ y$\Omega$.

Del Ejercicio 9.6.3, obtenemos eso$\ell \perp m$ si y solo si$\ell' \perp m'$.

Decimos que el círculo$\Gamma$ es perpendicular al círculo$\Omega$ (brevemente$\Gamma \perp \Omega$) si se cruzan y las líneas tangentes a los círculos en un punto (y por lo tanto, ambos puntos) de intersección son perpendiculares.

De igual manera, decimos que el círculo$\Gamma$ es perpendicular a la línea$\ell$ (brevemente$\Gamma \perp \ell$) si$\Gamma \cap \ell \ne \emptyset$ y$\ell$ perpendicular a las líneas tangentes a$\Gamma$ en un punto (y por lo tanto, ambos puntos) de intersección. Según Lemma 5.6.2, solo ocurre si la línea l pasa por el centro de$\Gamma$.

Ahora podemos hablar de circlinas perpendiculares.

Teorema$\PageIndex{1}$

Asumir$\Gamma$ y$Omega$ son círculos distintos. Entonces$\Omega \perp \Gamma$ si y sólo si el círculo$\Gamma$ coincide con su inversión en$\Omega$.

Prueba

Supongamos que$\Gamma'$ denota la inversa de$\Gamma$.

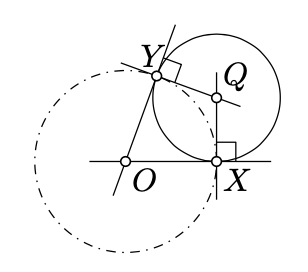
$2021-02-22 11.09.06.png$

“Sólo si” parte. Dejar$O$ ser el centro de$\Omega$ y$Q$ ser el centro de$\Gamma$. Dejar$X$ y$Y$ denotar los puntos de intersecciones de$\Gamma$ y$Omega$. Según Lemma 5.6.2,$\Omega \perp \Gamma$ si y sólo si$(OX)$ y$(OY)$ son tangentes a$\Gamma$.

Tenga en cuenta que también$\Gamma'$ es tangente a$(OX)$$(OY)$ y y$X$ y$Y$ respectivamente. De ello se deduce que$X$ y$Y$ son los puntos del pie del centro de$\Gamma'$ on$(OX)$ y$(OY)$. Por lo tanto, ambos$\Gamma'$ y$\Gamma$ tienen el centro$Q$. Por último,$\Gamma' = \Gamma$, ya que ambos círculos pasan a través$X$.

“Si” parte. Asumir$\Gamma = \Gamma'$.

Ya que$\Gamma \ne \Omega$, hay un punto$P$ que yace en$\Gamma$, pero no en$\Omega$. Dejar$P'$ ser la inversa de$P$ in$\Omega$. Ya que$\Gamma = \Gamma'$, tenemos eso$P' \in \Gamma$. En particular, la media línea$[OP)$ se cruza$\Gamma$ en dos puntos. Por el Ejercicio 5.6.1,$O$ se encuentra fuera de$\Gamma$.

Como$\Gamma$ tiene puntos dentro y fuera de$\Omega$, los círculos$\Gamma$ y se$\Omega$ cruzan. Este último se desprende del Ejercicio 3.5.1.

$X$Sea punto de su intersección. Tenemos que demostrar que$(OX)$ es tangente a$\Gamma$; es decir,$X$ es el único punto de intersección de$(OX)$ y$\Gamma$.

Supongamos que$Z$ es otro punto de intersección. Ya que$O$ está fuera de$\Gamma$, el punto$Z$ se encuentra en la media línea$[OX)$.

Supongamos que$Z'$ denota la inversa de$Z$ in$\Omega$. Claramente, los tres puntos$Z$,$Z'$,$X$ se encuentran sobre$\Gamma$ y$(OX)$. Este último contradice Lema 5.6.1.

Es conveniente definir la inversión en la línea$\ell$ como el reflejo a través$\ell$. De esta manera podemos hablar de inversión en una circlina arbitraria.

Corolario$\PageIndex{1}$

Dejar$\Omega$ y$\Gamma$ ser circlinos distintos en el plano inversivo. Entonces la inversión en$\Omega$ envía$\Gamma$ a sí misma si y sólo si$\Omega \perp \Gamma$.

Prueba

Por Thorem$\PageIndex{1}$, es suficiente considerar el caso cuando$\Omega$ o$\Gamma$ es una línea.

Asumir$\Omega$ es una línea, por lo que la inversión en$\Omega$ es un reflejo. En este caso el enunciado se desprende del Corolario 5.4.1.

Si$\Gamma$ es una línea, entonces la sentencia se desprende del Teorema 10.3.2.

Corolario$\PageIndex{2}$

Dejar$P$ y$P'$ ser dos puntos distintos tal que$P'$ sea la inversa de$P$ en el círculo$\Omega$. Supongamos que la circlina$\Gamma$ pasa a través$P$ y$P'$. Entonces$\Gamma \perp \Omega$.

Prueba

Sin pérdida de generalidad, podemos suponer que$P$ está dentro y$P'$ está afuera$\Omega$. Por Teorema 3.5.1,$\Gamma$ intersecta$\Omega$. Supongamos que A denota un punto de intersección.

Supongamos que$\Gamma'$ denota la inversa de$\Gamma$. Ya que$A$ es un auto inverso, los puntos$A, P$, y$P'$ se encuentran en$\Gamma'$. Por Ejercicio 8.1.1,$\Gamma'$ =$\Gamma$ y por Teorema$\PageIndex{1}$,$\Gamma \perp \Omega$.

Corolario$\PageIndex{3}$

Dejar$P$ y$Q$ ser dos puntos distintos dentro del círculo$\Omega$. Luego hay una circlina única$\Gamma$ perpendicular a la$\Omega$ que pasa a través$P$ y$Q$.

Prueba

Dejar$P'$ ser la inversa del punto$P$ en el círculo$\Omega$. Según Corolario$\PageIndex{2}$, la circlina está pasando a través$P$ y$Q$ es perpendicular a$\Omega$ si y solo si pasa a través$P'$.

Tenga en cuenta que$P'$ se encuentra fuera de$\Omega$. Por lo tanto, los puntos$P$$P'$,, y$Q$ son distintos.

De acuerdo con el Ejercicio Ejercicio 8.1.1, hay una circlina única que pasa a través$P, Q$, y$P'$. De ahí el resultado.

Ejercicio$\PageIndex{1}$

Dejar$P, Q, P'$, y$Q'$ ser puntos en el plano euclidiano. Asumir$P'$ y$Q'$ son inversos de$P$ y$Q$ respectivamente. Demostrar que el cuadrilátero$PQP'Q'$ está inscrito.

Pista: Aplicar Teorema 10.2.1, Teorema 7.4.5 y Teorema 9.2.1.

Ejercicio$\PageIndex{2}$

Dejar$\Omega_1$ y$\Omega_2$ ser dos círculos perpendiculares con centros en$O_1$ y$O_2$ respectivamente. Mostrar que la inversa de$O_1$ in$\Omega_2$ coincide con la inversa de$O_2$ in$\Omega_1$.

Pista: Supongamos que$T$ denota un punto de intersección de$\Omega_1$ y$\Omega_2$. Deja$P$ ser el punto del pie de$T$ on$(O_1O_2)$. $\triangle O_1PT \sim \triangle O_1TO_2 \sim \triangle TPO_2$Demuéstralo. Considera que$P$ coincide con las inversas de$O_1$ in$\Omega_2$ y de$O_2$ in$\Omega_1$.

Ejercicio$\PageIndex{3}$

Tres círculos distintos$\Omega_1$ —,$\Omega_2$ y$\Omega_3$, se cruzan en dos puntos—$A$ y$B$. Supongamos que un círculo$\Gamma$ es perpendicular a$\Omega_1$ y$\Omega_2$. $\Gamma \perp \Omega_3$Demuéstralo.

Pista: Desde$\Gamma \perp \Omega_1$ y$\Gamma \perp \Omega_2$, Corolario$PageIndex{1}$ implica que los círculos$\Omega_1$ y$\Omega_2$ están invertidos en$\Gamma$ sí mismos. Concluir que los puntos$A$ y$B$ son inversos entre sí. Ya que$\Omega_3 \ni A, B$, Corolario$\PageIndex{2}$ implica eso$\Omega_3 \perp \Gamma$.

Consideremos dos nuevas herramientas de construcción: la circunherramienta que construye una circlina a través de tres puntos dados, y la herramienta de inversión, una herramienta que construye una inversa de un punto dado en una circlina dada.

Ejercicio$\PageIndex{4}$

Dados dos círculos$\Omega_1$,$\Omega_2$ y un punto$P$ que no se encuentra en los círculos, utilizar sólo circun-herramienta y herramienta de inversión para construir una circlina$\Gamma$ que pasa a través$P$, y perpendicular a ambos$\Omega_1$ y$\Omega_2$.

Pista

Dejar$P_1$ y$P_2$ ser la inversa de$P$ in$\Omega_1$ y$\Omega_2$. Aplicar Corolario$\PageIndex{2}$ y Teorema$\PageIndex{1}$ para demostrar que una circlina$\Gamma$ que pasa a través

$P, P_1$, y$P_3$ es una solución.

Ejercicio Avanzado$\PageIndex{5}$

Dados tres círculos$\Omega_1$ disjuntos$\Omega_3$,$\Omega_2$ y, utilizar sólo circun-herramienta y herramienta de inversión para construir una circlina$\Gamma$ que perpendicular a cada círculo$\Omega_1$,$\Omega_2$ y$\Omega_3$.

Piensa qué hacer si dos de los círculos se cruzan.

Pista

Todos los círculos que perpendiculares a$\Omega_1$ y$\Omega_2$ pasan a través de un punto fijo$P$. Intenta construir$P$.

Si dos de los círculos se cruzan, intente aplicar el Corolario 10.6.1.

Teorema\(\PageIndex{1}\)

Corolario\(\PageIndex{1}\)

Corolario\(\PageIndex{2}\)

Corolario\(\PageIndex{3}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio Avanzado\(\PageIndex{5}\)