3.2: Otros cuadriláteros

En esta sección consideraremos otros cuadriláteros con propiedades especiales: el rombo, el rectángulo, el cuadrado y el trapecio.

Figura\(\PageIndex{1}\): Un rombo.

Figura\(\PageIndex{2}\): Un rombo con diagonales.

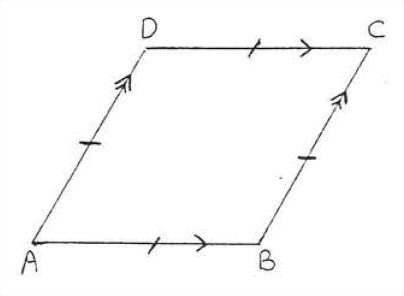
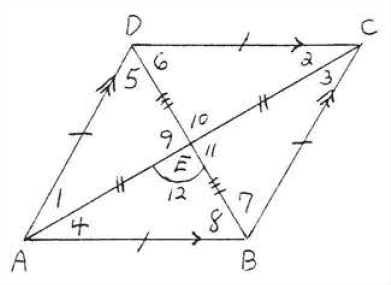
Un rombo es un paralelogramo en el que todos los lados son iguales (Figura\(\PageIndex{1}\)). Tiene todas las propiedades de un paralelogramo más algunas adicionales también. Dibujemos las diagonales\(AC\) y\(BD\) (Figura\(\PageIndex{2}\)). Por Teorema\(\PageIndex{3}\) de la sección 3.1 las diagonales se bisecan entre sí. De ahí

\[\triangle ADE \cong \triangle CDE \cong \triangle CBE \cong \triangle ABE \nonumber\]

por\(SSS = SSS\). Los ángulos correspondientes de los triángulos congruentes son iguales:

\[\angle 1 = \angle 2 = \angle 3 = \angle 4, \nonumber\]

\[\angle 5 = \angle 6 = \angle 7 = \angle 8 \nonumber\]

y

\[\angle 9 = \angle 10 = \angle 11 = \angle 12. \nonumber\]

\(\angle 9\)y\(\angle 10\) son complementarios además de ser iguales, de ahí\(\angle 9 = \angle 10 = \angle 11 = \angle 12 = 90^{\circ}\). Hemos probado el siguiente teorema:

Teorema\(\PageIndex{1}\)

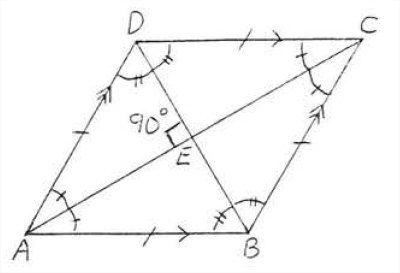
Las diagonales de un rombo son perpendiculares y bisecan los ángulos. Ver Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Las diagonales de un rombo son perpendiculares y bisecan los ángulos.

Ejemplo\(\PageIndex{1}\)

Buscar\(w\),\(x\),\(y\), y\(z\):

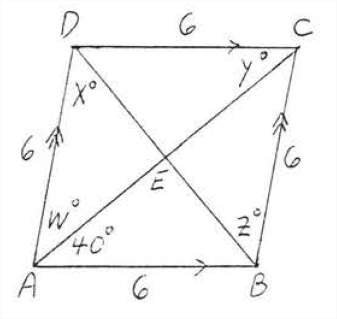
Solución

\(ABCD\)es un rombo ya que es un paralelogramo todos cuyos lados equivalen a 6. Según el Teorema\(\PageIndex{1}\), las diagonales son perpendiculares y bisecan los ángulos. Por lo tanto\(w^{\circ}=40^{\circ}\) desde\(AC\) bisectas\(\angle BAD\). \(\angle AED = 90^{\circ}\)so\(x^{\circ} = 180^{\circ} - (90^{\circ} + 40^{\circ}) = 180^{\circ} - 130^{\circ} = 50^{\circ}\) (la suma de los ángulos de\(\angle AED\) es\(180^{\circ}\)). Finalmente\(y^{\circ} = w^{\circ} = 40^{\circ}\) (comparar con la Figura\(\PageIndex{3}\)) y\(z^{\circ} = x^{\circ} = 50^{\circ}\).

Contestar

\(w = 40, x = 50, y = 40, z = 50\).

La figura\(\PageIndex{4}\) muestra el rombo\(ABCD\) del Ejemplo\(\PageIndex{1}\) con todos sus ángulos identificados.

Figura\(\PageIndex{4}\): El rombo del Ejemplo\(\PageIndex{1}\) con todos los ángulos identificados.

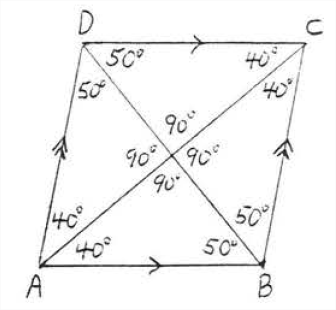
Un rectángulo es un paralelogramo en el que todos los ángulos son ángulos rectos (Figura\(\PageIndex{5}\)). Tiene todas las propiedades de un paralelogramo más algunas adicionales también. En realidad no es necesario que se le diga que todos los ángulos son ángulos rectos:

Figura\(\PageIndex{5}\): Un rectángulo.

Figura\(\PageIndex{6}\): Un paralelogramo con solo un ángulo recto también debe ser un rectángulo.

Teorema\(\PageIndex{2}\)

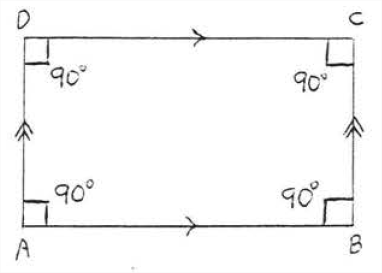
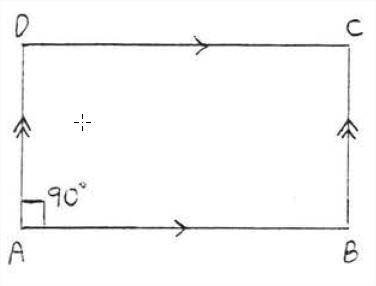
Un paralelogramo con solo un ángulo recto debe ser un rectángulo.

En la Figura\(\PageIndex{6}\) si\(\angle A\) es un ángulo recto entonces todos los demás ángulos deben ser ángulos rectos también.

Prueba

En la Figura\(\PageIndex{6}\),\(\angle C = \angle A = 90^{\circ}\) porque los ángulos opuestos de un paralelogramo son iguales (Teorema\(\PageIndex{1}\), sección 3.1). \(\angle B = 90^{\circ}\)y\(\angle D = 90^{\circ}\) porque los ángulos sucesivos de un paralelogramo son complementarios (Teorema\(\PageIndex{2}\), sección 3.2).

Ejemplo\(\PageIndex{2}\)

Encuentra\(x\) y\(y\):

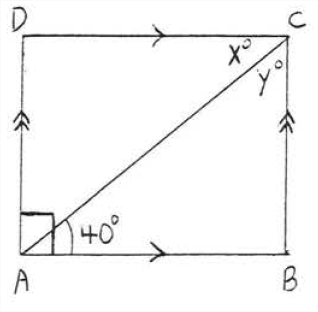
Solución

Teorema\(\PageIndex{2}\),\(ABCD\) es un rectángulo. \(x^{\circ}=40^{\circ}\)porque alternan ángulos interiores de líneas paralelas\(AB\) y\(CD\) deben ser iguales. Dado que la figura es un rectángulo\(\angle BCD = 90^{\circ}\) y\(y^{\circ} = 90^{\circ} - x^{\circ} = 90^{\circ} - 40^{\circ} = 50^{\circ}.\)

Respuesta:\(x = 40, y = 50\)

Dibujemos las diagonales del rectángulo\(ABCD\) (Figura\(\PageIndex{7}\)).

Figura\(\PageIndex{7}\): Rectángulo con diagonales dibujadas.

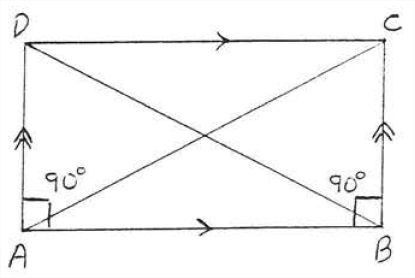
Vamos a mostrar\(\triangle ABC \cong \triangle BAD\). \(AB = BA\)por identidad. \(\angle A = \angle B = 90^{\circ}\). \(BC = AD\)porque los lados opuestos de un paralelogramo son iguales. Entonces\(\triangle ABC \cong \triangle BAD\) por\(SAS = SAS\). Por lo tanto\(AC =\) diagonal diagonal\(B D\) porque son lados correspondientes de triángulos congruentes. Hemos probado:

Teorema\(\PageIndex{3}\)

Las diagonales de un rectángulo son iguales. En la Figura\(\PageIndex{7}\),\(AC = BD\).

Ejemplo\(\PageIndex{3}\)

Buscar\(w\),\(x\)\(y\),\(z\),\(AC\) y\(BD\):

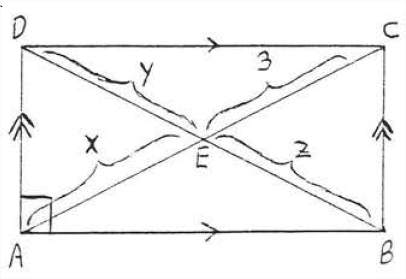
Solución

\(x = 3\)porque las diagonales de un paralelogramo se bisecan entre sí. Entonces\(AC = 3 + 3 = 6\). \(BD = AC = 6\)ya que las diagonales de un rectángulo son iguales (Teorema\(\PageIndex{3}\)). Por lo tanto\(y = z = 3\) ya que diagonal\(BD\) es biseccionada por diagonal\(AC\).

Respuesta:\(x= y = z = 3\) y\(AC = BD = 6\).

Ejemplo\(\PageIndex{4}\)

Buscar\(x\),\(y\), y\(z\):

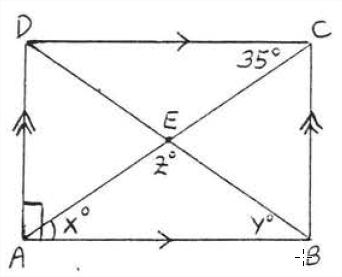
Solución

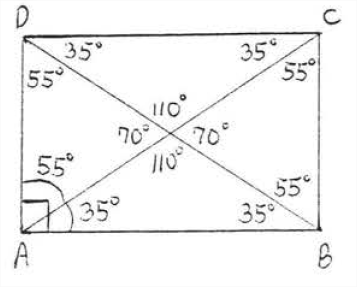
\(x^{\circ} = 35^{\circ}\), porque los ángulos interiores alternos de las líneas paralelas son iguales. \(y^{\circ} = x^{\circ} = 35^{\circ}\)porque son ángulos base del triángulo isósceles\(ABE\) así (AE= BE\) porque las diagonales de un rectángulo son iguales y se bisecan entre sí). \(z^{\circ} = 180^{\circ} - (x^{\circ} + y^{\circ}) = 180^{\circ} - (35^{\circ} + 35^{\circ}) = 180^{\circ} - 70^{\circ} = 110^{\circ}\). La figura\(\PageIndex{8}\) muestra un rectángulo\(ABCD\) con todos los ángulos identificados.

Respuesta:\(x=y=z=3, A C=B D=6\).

Figura\(\PageIndex{8}\): El rectángulo de Ejemplo\(\PageIndex{4}\) con todos los ángulos identificados.

La Plaza

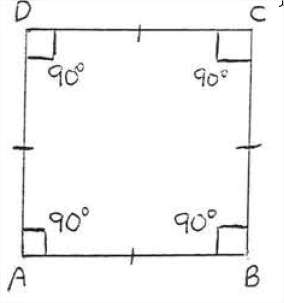
Un cuadrado es un rectángulo con todos sus lados iguales. Por lo tanto, también es un rombo. Por lo que tiene todas las propiedades del rectángulo y todas las propiedades del rombo.

Figura\(\PageIndex{9}\): Un cuadrado.

Figura\(\PageIndex{10}\): Un trapecio.

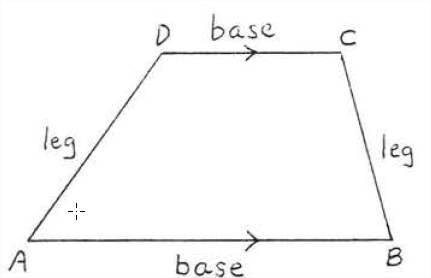
Un trapecio es un cuadrilátero con dos y sólo dos lados paralelos. Los lados paralelos se llaman bases y los otros dos lados se llaman patas. En Figura\(\PageIndex{8}\)\(AB\) y\(CD\) están las bases y\(AD\) y\(BC\) son las patas. \(\angle A\)y\(\angle B\) son un par de ángulos de base. \(\angle C\)y\(\angle D\) son otro par de ángulos de base.

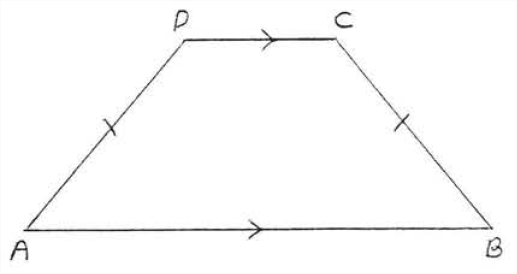
Un trapecio isósceles es un trapecio en el que las patas son iguales. En la Figura\(\PageIndex{8}\),\(ABCD\) es un trapecio isósceles con\(AD = BC\). Un trapecio isósceles tiene la siguiente propiedad:

Teorema\(\PageIndex{4}\)

Los ángulos de base de un trapecio isósceles son iguales. En la Figura\(\PageIndex{11}\),\(\angle A = \angle B\) y\(\angle C = \angle D\)

Figura\(\PageIndex{11}\): Un trapecio isósceles

Ejemplo\(\PageIndex{5}\)

Encontrar\(x, y\), y\(z:\)

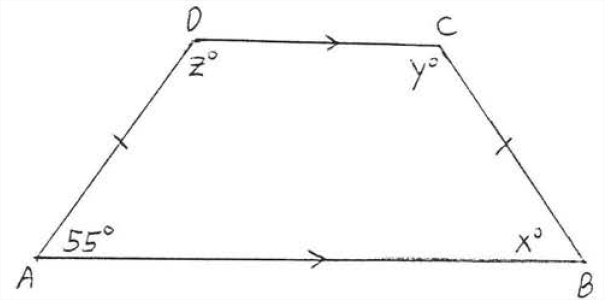
Solución

\(x^{\circ}=55^{\circ}\)porque\(\angle A\) y\(\angle B\), los ángulos base del trapecio isósceles\(ABCD\), son iguales. Ahora los ángulos interiores de líneas paralelas en el mismo lado de la transversal son suplementarios (Teorema 3 sección 1.4). Por lo tanto\(y^{\circ} = 180^{\circ} - x^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}\) y\(z^{\circ} = 180^{\circ} - 55^{\circ} = 125^{\circ}\).

Respuesta:\(x = 22\),\(y = z = 125\).

Prueba de teorema\(\PageIndex{4}\): Draw \(DE\) parallel to \(CB\) as in Figure \(\PageIndex{12}\). \(\angle 1 = \angle B\) because corresponding angles of parallel lines are equal, \(DE = BC\) because they are the opposite sides of parallelogram \(BCDE\). Therefore \(AD = DE\). So \(\triangle ADE\) is isosceles and its base angles, \(\angle A\) and \(\angle 1\), are equal. We have proven \(A = \angle 1 = \angle B\). To prove \(\angle C = \angle D\), observe that they are both supplements of \(\angle A = \angle B\) (Theorem \(\PageIndex{3}\), section 1.4).

El trapecio isósceles tiene una propiedad adicional:

Teorema\(\PageIndex{5}\)

Las diagonales de un trapecio isosecles son iguales.

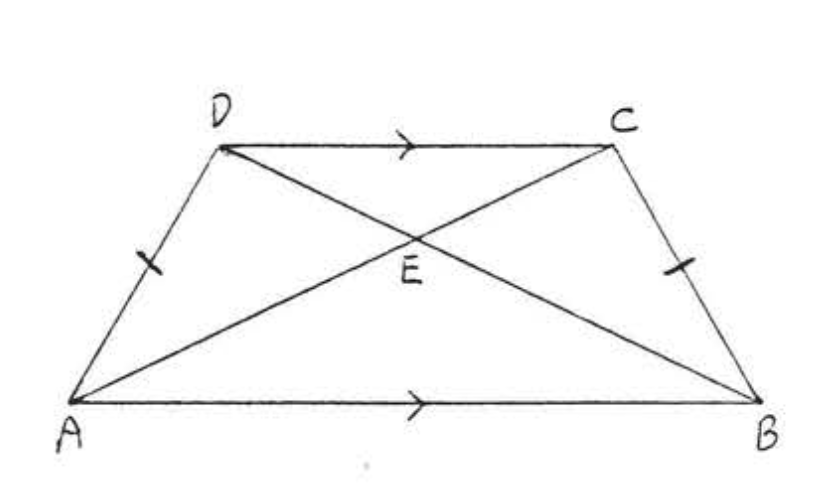
En la Figura\(\PageIndex{13}\), \(AC = BD\)

Figura\(\PageIndex{13}\). The diagonals \(AC\) and \(BD\) are equal.

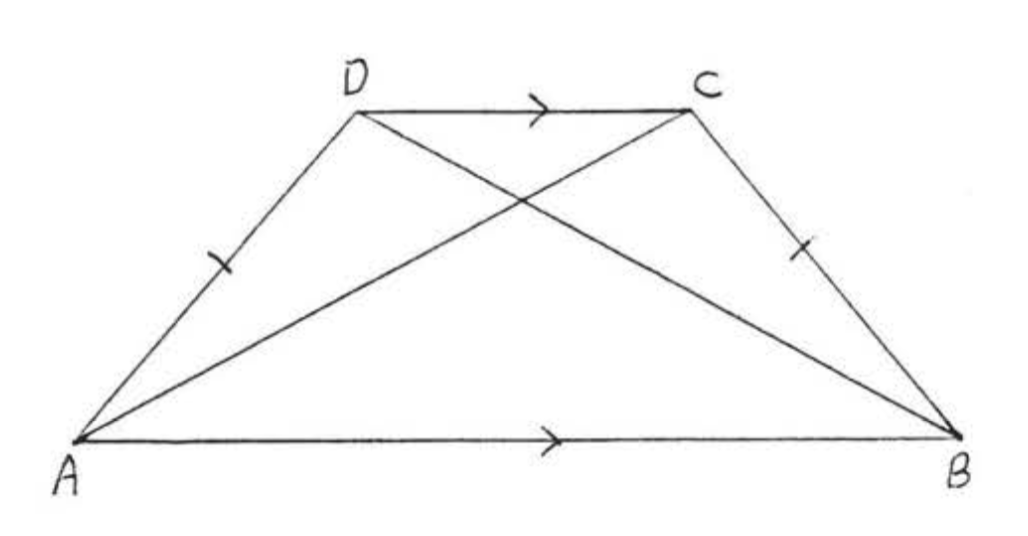
Prueba

\(BC = AD\), dado,\(\angle ABC = \angle BAD\) porque son los ángulos base del trapecio isósceles\(ABCD\) (Teorema\(\PageIndex{4}\)). \(AB = BA\), identity. Therefore \(\triangle ABC \cong \triangle BAD\) by \(SAS = SAS\). So \(AC = BD\) because they are corresponding sides of the congruent triangles.

Ejemplo\(\PageIndex{6}\)

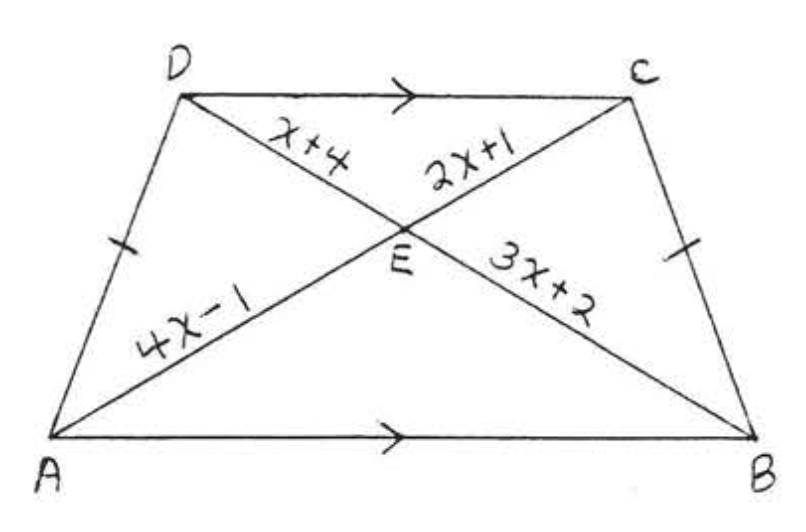
Averigua\(x\) si\(AC = \dfrac{2}{x}\) y\(BD = 3 - x\):

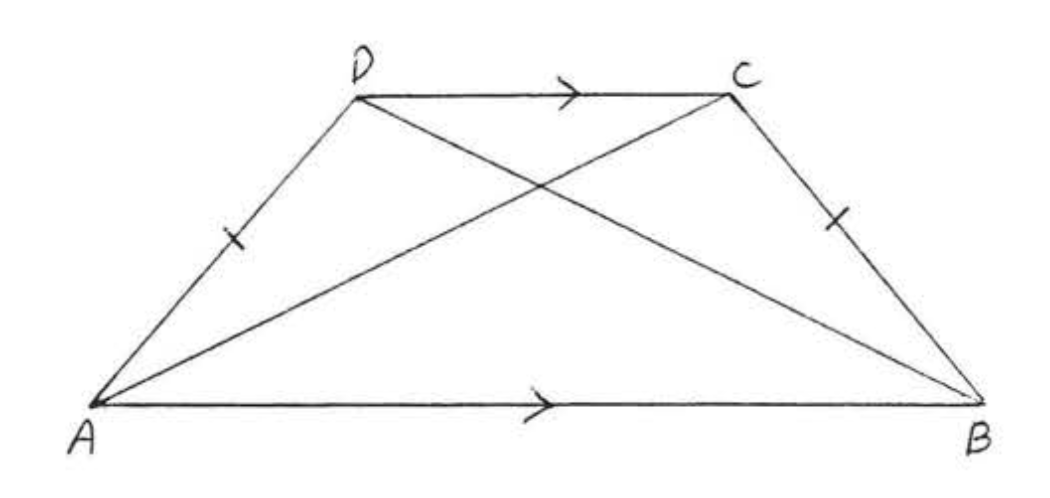
Solución

Por teorema\(\PageIndex{5}\),

\(\begin{array} {rcl} {AC} & = & {BD} \\ {\dfrac{2}{x}} & = & {3 - x} \\ {(x)\dfrac{2}{x}} & = & {(3 - x)(x)} \\ {2} & = & {3x - x^2} \\ {x^2 - 3x + 2} & = & {0} \\ {(x - 1)(x - 2)} & = & {0} \end{array}\)

\(\begin{array} {rcl} {x - 1} & = & {0} \\ {x} & = & {1} \end{array}\)\(\begin{array} {rcl} {x - 2} & = & {0} \\ {x} & = & {2} \end{array}\)

Comprobar,\(x = 1\):

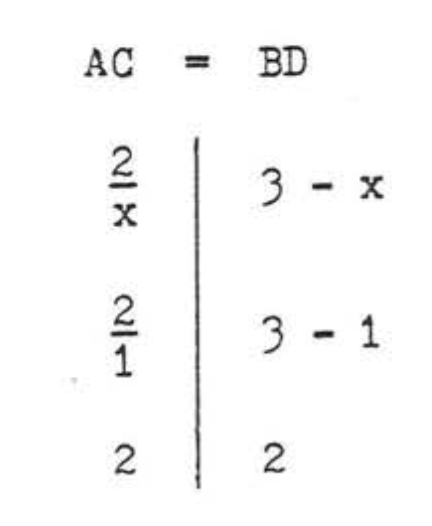
Comprobar,\(x = 2\):

Respuesta:\(x = 1\) or \(x = 2\).

RESUMEN

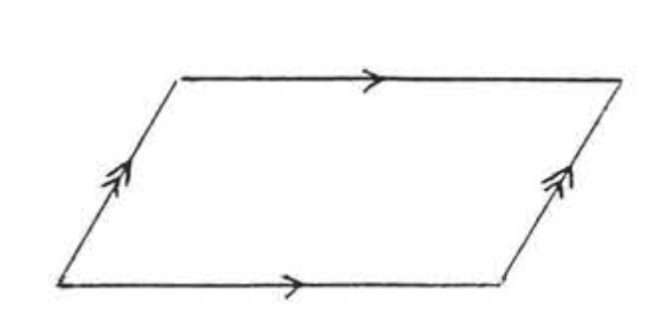
EL PARALELOGRAMO

Un cuadrilátero en el que los lados opuestos son paralelos.

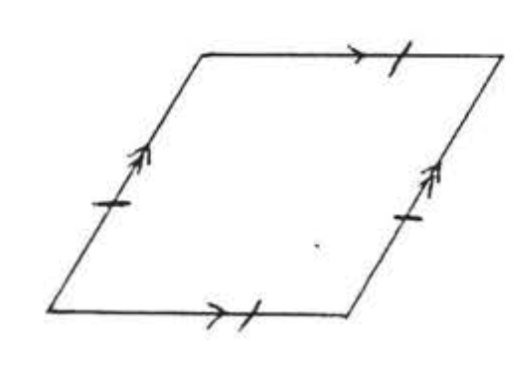
EL ROMBO

Un paralelogramo en el que todos los lados son iguales.

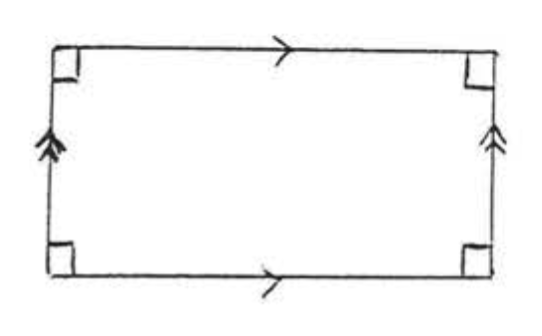
EL RECTÁNGULO

Un paralelogramo en el que todos los ángulos son iguales a\(90^{\circ}\).

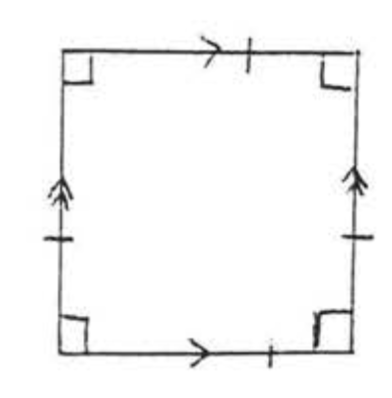
LA PLAZA

Un paralelogramo que es a la vez un rombo y un rectángulo.

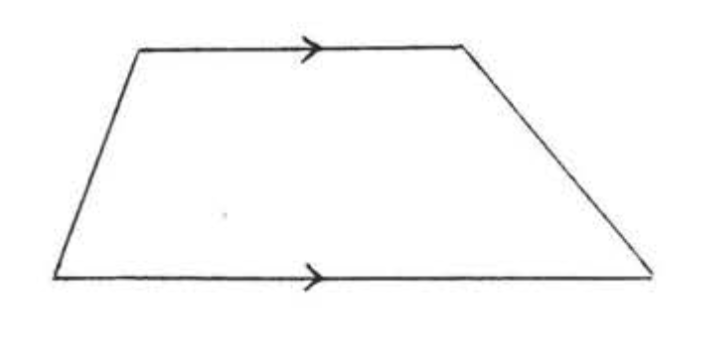
EL TRAPECIO

Un cuadrilátero con solo un par de lados paralelos.

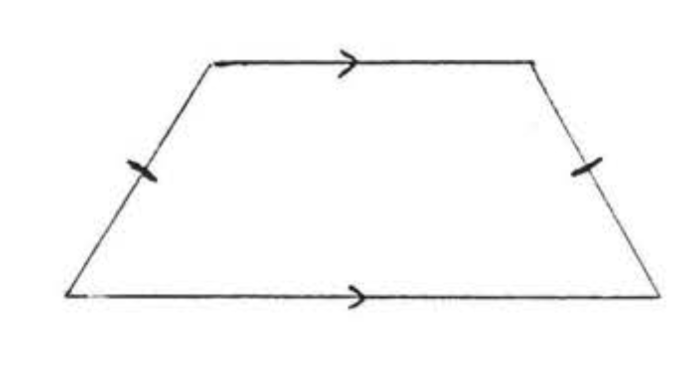
EL TRAPECIO ISÓSCELES

Un trapecio en el que los lados no paralelos son iguales.

PROPIEDADES DE CUADRILÁTEROS

	Los lados opuestos son paralelos	Los lados opuestos son iguales	Ángulos opuestos	Las diagonales se bisecan entre sí	Las diagonales son iguales	Las diagonales son perpendiculares	Las diagonales bisecan los ángulos	Todos los lados son iguales	Todos los ángulos son iguales
Paralelogramo	SI	SI	SI	SI	-	-	-	-	-
Rombo	SI	SI	SI	SI	-	SI	SI	SI	-
Rectángulo	SI	SI	SI	SI	SI	-	-	-	SI
Trapezoide	*	-	-	-	-	-	-	-	-
Trapezoide isósceles	*	*	-	-	SI	-	-	-	-

*Un solo par.

Problemas

Para cada uno de los siguientes estados cualquier teorema utilizado en la obtención de su respuesta.

1. Buscar\(w, x, y\), y\(z\):

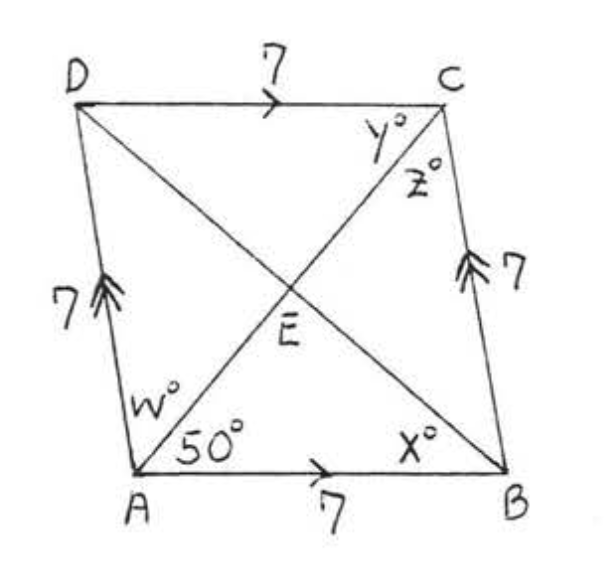
2. Buscar\(w, x, y\), y\(z\):

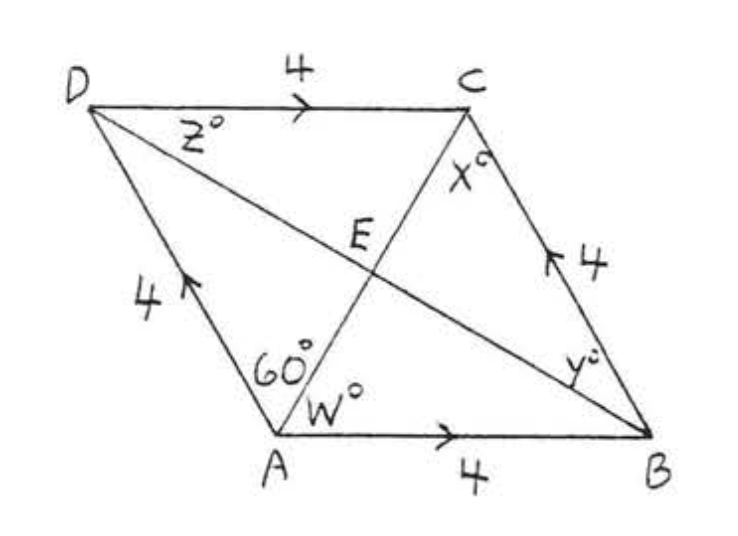
3. Encuentra\(x\) y\(y\):

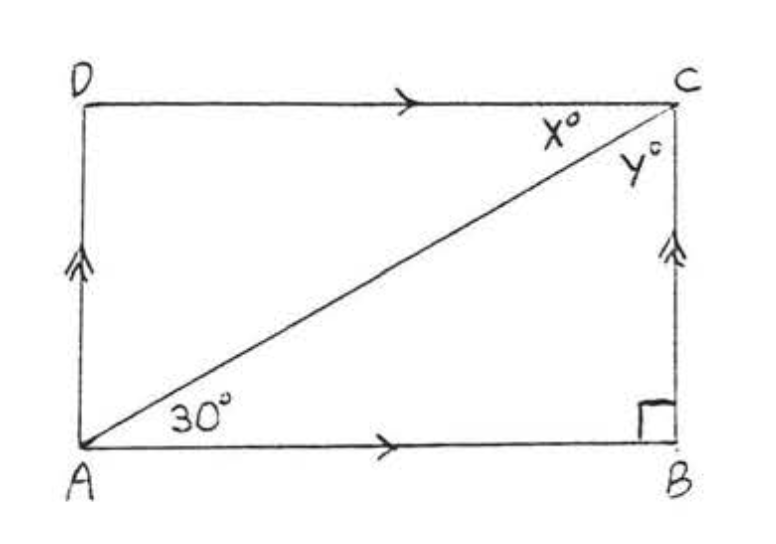
4. Encuentra\(x\) y\(y\):

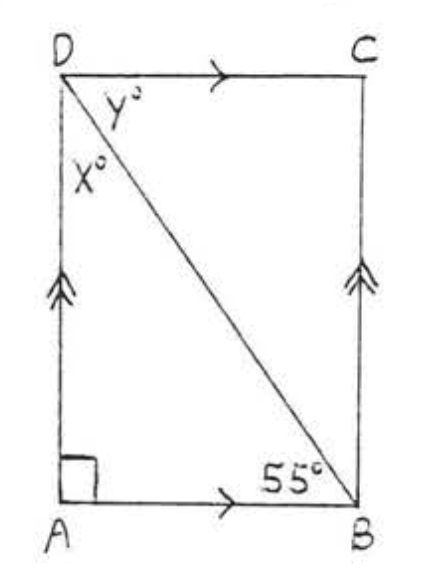
5. Encuentra\(x, y, z, AC\) y\(BD\):

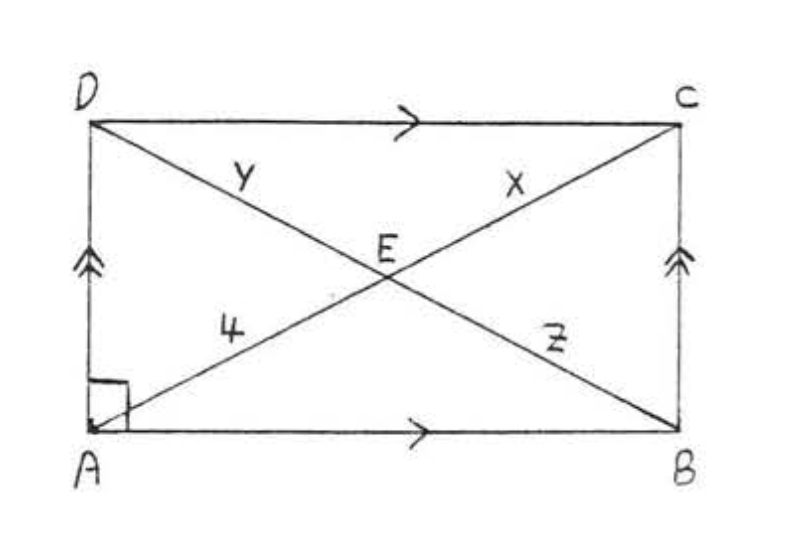
6. Buscar\(x, y\), y\(z\):

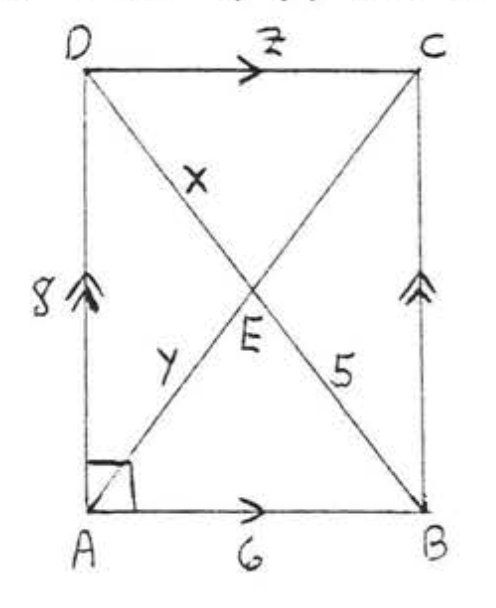
7. Buscar\(x, y\), y\(z\):

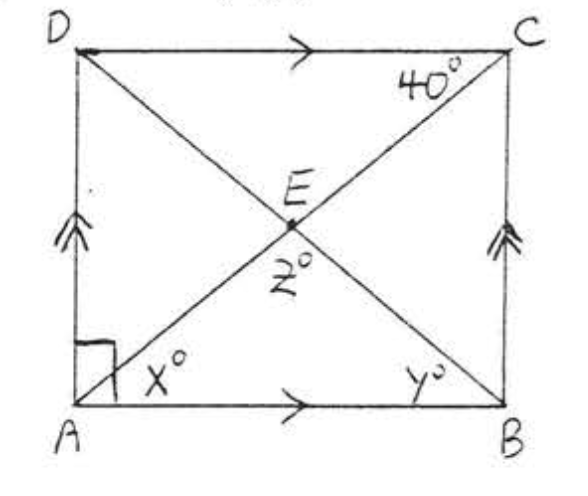
8. Buscar\(x, y\), y\(z\):

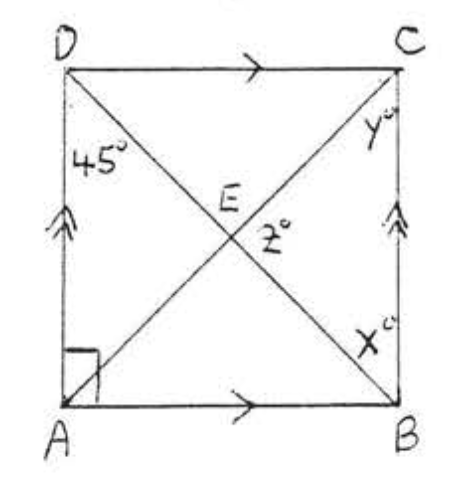
9. Averigua\(x\) si\(AC = \dfrac{3}{x}\) y\(BD = 4x - 1\):

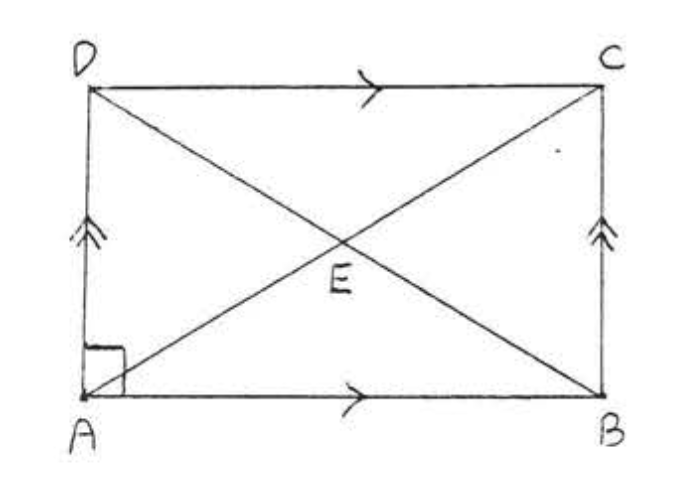
10. Encuentra\(x\) y\(y\):

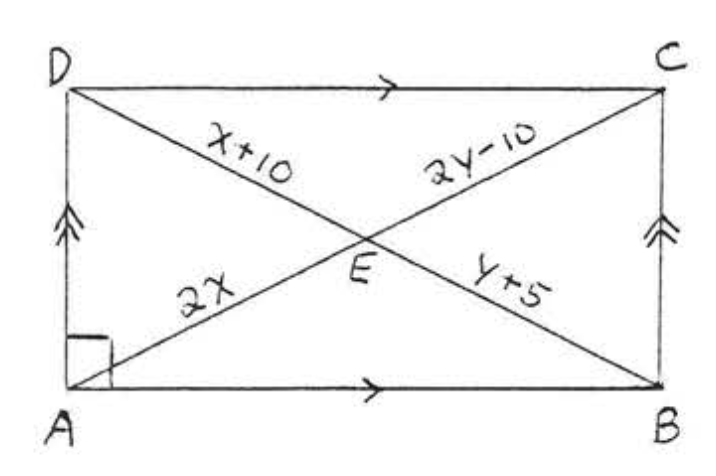
11. Buscar\(x, y\), y\(z\):

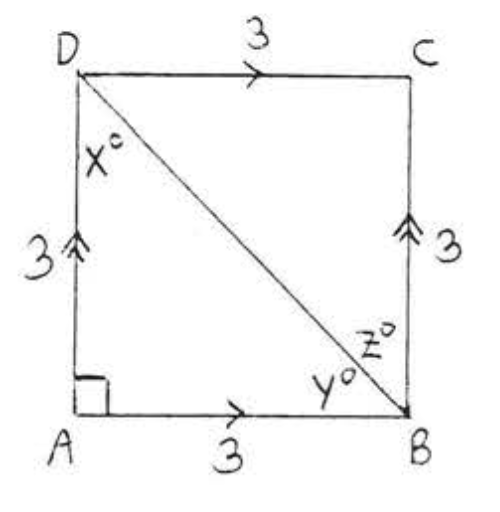
12. Buscar\(x, y\), y\(z\):

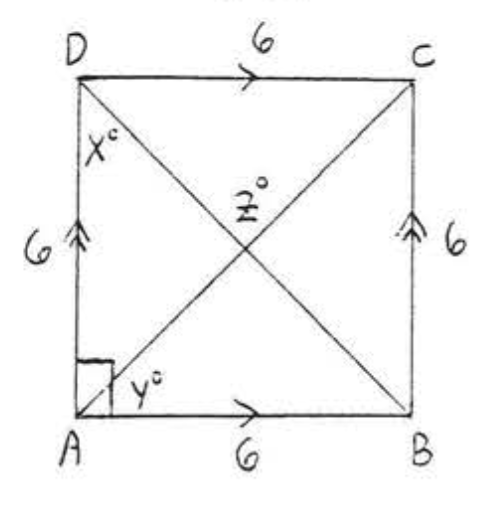
13. Buscar\(x, y\), y\(z\):

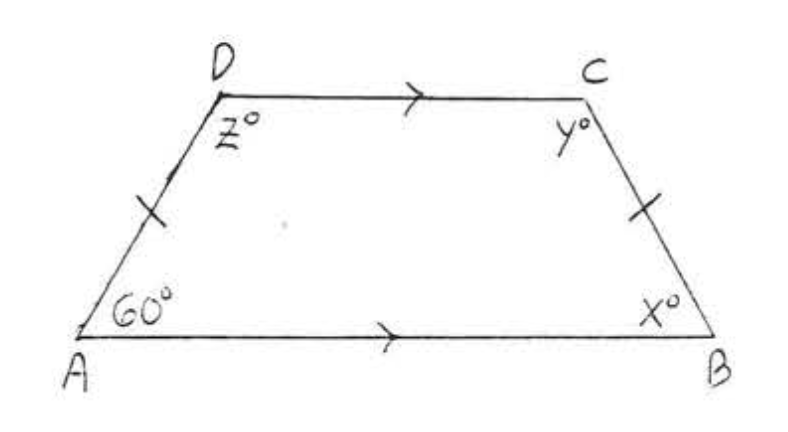
14. Buscar\(x, y\), y\(z\):

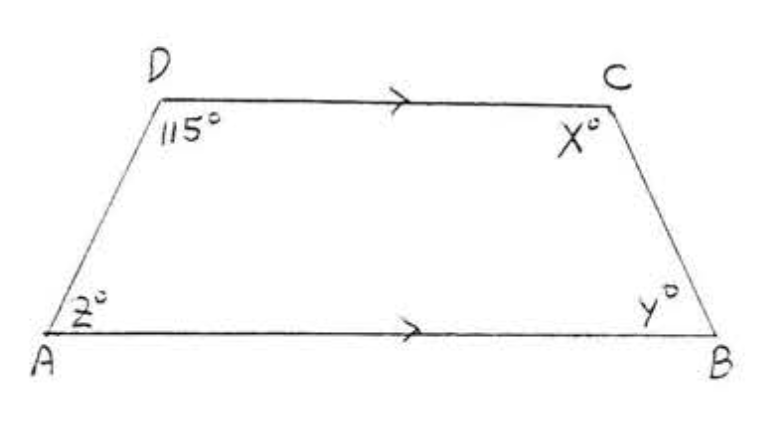
15. Encuentra\(x\) y\(y\):

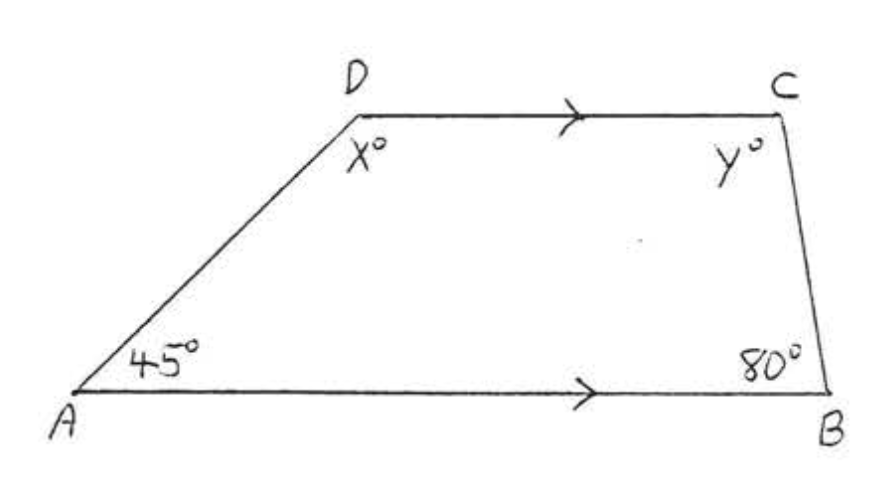
16. Buscar\(x, y, \angle A, \angle B, \angle C\), y\(\angle D\):

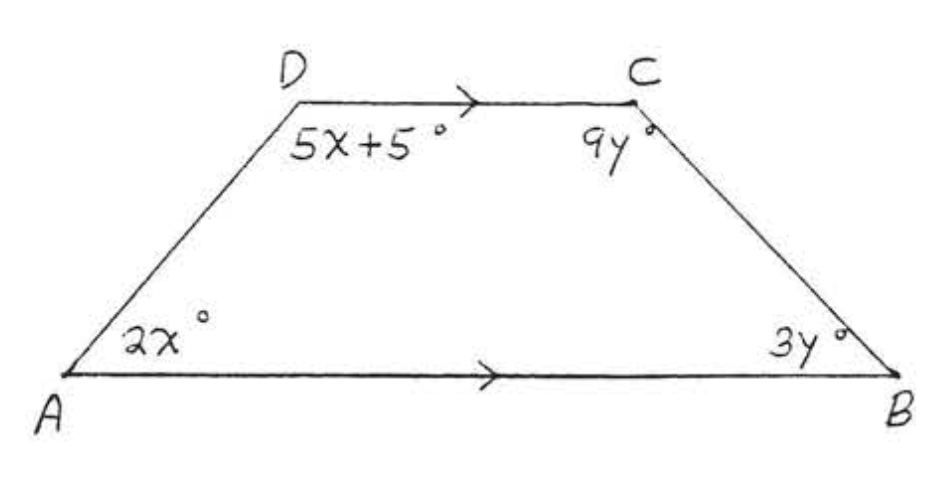
17. Buscar\(w, x, y\), y\(z\):

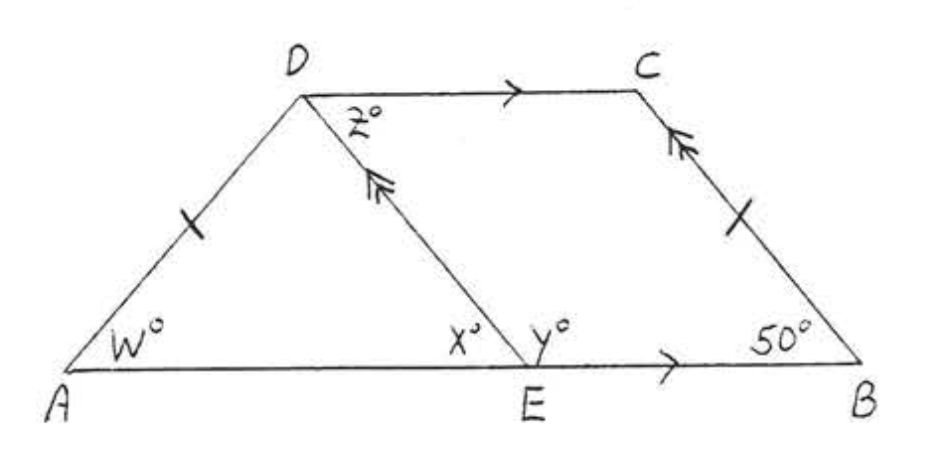
18. Buscar\(x, y\), y\(z\):

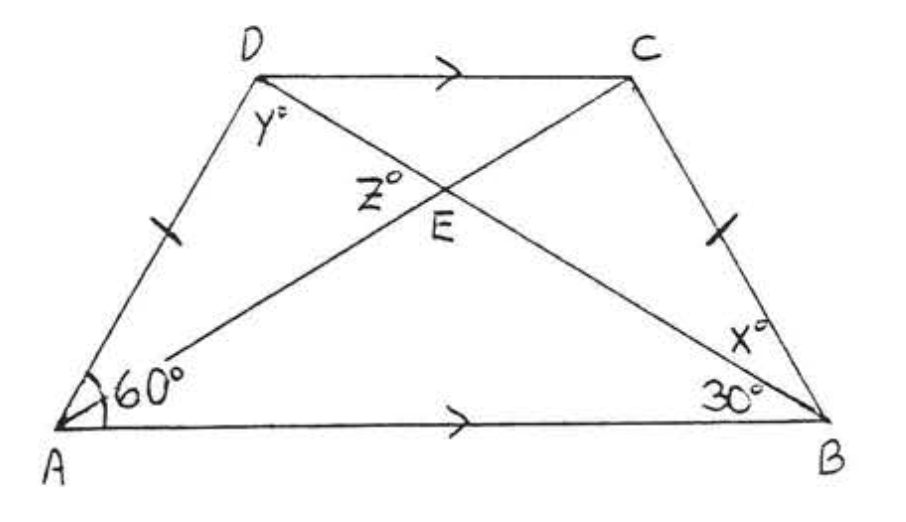
19. Averigua\(x\) si\(AC = x^2 - 13\) y\(BD = 2x + 2\):

20. Buscar\(x\),\(AC\) y\(BD\):