3.4: Triángulos, rectángulos y teorema de Pitágoras
( \newcommand{\kernel}{\mathrm{null}\,}\)
Al final de esta sección, podrás:
- Resolver aplicaciones usando propiedades de triángulos
- Usa el Teorema de Pitágoras
- Resolver aplicaciones usando propiedades de rectángulo
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:12(6h).
Si te perdiste este problema, revisa el Ejercicio 1.10.1. - La longitud de un rectángulo es tres menos que el ancho. Deje que w represente el ancho. Escribe una expresión para la longitud del rectángulo.
Si te perdiste este problema, revisa Ejercicio 1.3.43. - Resolver:A=12bh para b cuando A=260 y h=52.
Si te perdiste este problema, revisa el Ejercicio 2.6.10. - Simplificar:√144.
Si te perdiste este problema, revisa Ejercicio 1.9.10.
Resolver aplicaciones usando propiedades de triángulos
En esta sección utilizaremos algunas fórmulas de geometría comunes. Adaptaremos nuestra estrategia de resolución de problemas para que podamos resolver aplicaciones de geometría. La fórmula de geometría nombrará las variables y nos dará la ecuación a resolver. Además, dado que todas estas aplicaciones involucrarán formas de algún tipo, a la mayoría de las personas les resulta útil dibujar una figura y etiquetarla con la información dada. Incluiremos esto en el primer paso de la estrategia de resolución de problemas para aplicaciones de geometría.
- Lee el problema y asegúrate de que se entiendan todas las palabras e ideas. Dibuja la figura y etiquétela con la información dada.
- Identificar lo que estamos buscando.
- Etiquetar lo que estamos buscando eligiendo una variable para representarlo.
- Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Verifique la respuesta sustituyéndola de nuevo en la ecuación resuelta en el paso 5 y asegurándose de que tenga sentido en el contexto del problema.
- Contesta la pregunta con una oración completa.
Comenzaremos aplicaciones de geometría observando las propiedades de los triángulos. Repasemos algunos datos básicos sobre los triángulos. Los triángulos tienen tres lados y tres ángulos interiores. Por lo general, cada lado está etiquetado con una letra minúscula para que coincida con la letra mayúscula del vértice opuesto.
El plural de la palabra vértice es vértices. Todos los triángulos tienen tres vértices. Los triángulos son nombrados por sus vértices: El triángulo en la Figura3.4.1 se llama△ABC.
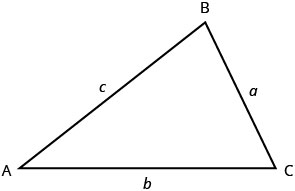
Los tres ángulos de un triángulo están relacionados de manera especial. La suma de sus medidas es180∘. Tenga en cuenta que leemosm∠A como “la medida del ángulo A.” Así que△ABC en Figura3.4.1.
m∠A+m∠B+m∠C=180∘
Debido a que el perímetro de una figura es la longitud de su límite, el perímetro de△ABC es la suma de las longitudes de sus tres lados.
P=a+b+c
Para encontrar el área de un triángulo, necesitamos conocer su base y altura. La altura es una línea que conecta la base con el vértice opuesto y hace un90∘ ángulo con la base. Volveremos△ABC a dibujar, y ahora mostrar la altura,h. Ver Figura3.4.2.
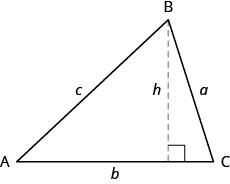
Para△ABC
Medidas del ángulo:
m∠A+m∠B+m∠C=180∘
- La suma de las medidas de los ángulos de un triángulo es de 180°.
Perímetro:
P=a+b+c
- El perímetro es la suma de las longitudes de los lados del triángulo.
Área:
A=12bh,b= base ,h= height
- El área de un triángulo es la mitad de la base por la altura.
Las medidas de dos ángulos de un triángulo son 55 y 82 grados. Encuentra la medida del tercer ángulo.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 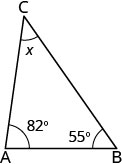 |
| Paso 2. Identifica lo que buscas. | la medida del tercer ángulo en un triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja quex= la medida del ángulo. |
| Paso 4. Traducir. | |
| Escribir la fórmula apropiada y sustituirla. | m∠A+m∠B+m∠C=180∘ |
| Paso 5. Resuelve la ecuación. | 55+82+x=180137+x=180x=43 |
| Paso 6. Cheque. 55+82+43?=180180=180✓ |
|
| Paso 7. Contesta la pregunta. | La medida del tercer ángulo es de 43 grados. |
Las medidas de dos ángulos de un triángulo son 31 y 128 grados. Encuentra la medida del tercer ángulo.
- Responder
-
21 grados
Las medidas de dos ángulos de un triángulo son 49 y 75 grados. Encuentra la medida del tercer ángulo.
- Responder
-
56 grados
El perímetro de un jardín triangular es de 24 pies. Las longitudes de dos lados son cuatro pies y nueve pies. ¿Cuánto dura el tercer lado?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 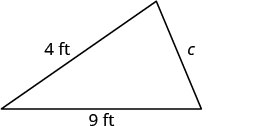  |
| Paso 2. Identifica lo que buscas. | longitud del tercer lado de un triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja quec= el tercer lado. |
| Paso 4. Traducir. | |
| Escribir la fórmula apropiada y sustituirla. | 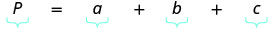 |
| Sustituir en la información dada. | 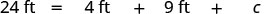 |
| Paso 5. Resuelve la ecuación. |   |
| Paso 6. Cheque. P=a+b+c24?=4+9+1124=24✓ |
|
| Paso 7. Contesta la pregunta. | El tercer lado mide 11 pies de largo. |
El perímetro de un jardín triangular es de 48 pies. Las longitudes de dos lados son de 18 pies y 22 pies. ¿Cuánto dura el tercer lado?
- Responder
-
8 pies
Las longitudes de dos lados de una ventana triangular son de siete pies y cinco pies. El perímetro es de 18 pies. ¿Cuánto dura el tercer lado?
- Responder
-
6 pies
El área de una ventana triangular de iglesia es de 90 metros cuadrados. La base de la ventana es de 15 metros. ¿Cuál es la altura de la ventana?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 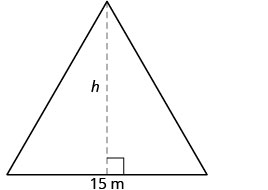 Area =90m2 |
| Paso 2. Identifica lo que buscas. | altura de un triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja queh= la altura. |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. |  |
| Sustituir en la información dada. |  |
| Paso 5. Resuelve la ecuación. | 90=152h 12=h |
| Paso 6. Cheque. A=12bh90?=12⋅15⋅1290=90✓ |
|
| Paso 7. Contesta la pregunta. | La altura del triángulo es de 12 metros. |
El área de una pintura triangular es de 126 pulgadas cuadradas. La base es de 18 pulgadas. ¿Cuál es la altura?
- Responder
-
14 pulgadas
Una puerta triangular para tienda tiene un área de 15 pies cuadrados. La altura es de cinco pies. ¿Cuál es la base?
- Responder
-
6 pies
Las propiedades del triángulo que hemos usado hasta ahora se aplican a todos los triángulos. Ahora veremos un tipo específico de triángulo: un triángulo rectángulo. Un triángulo rectángulo tiene un ángulo de 90°, que generalmente marcamos con un pequeño cuadrado en la esquina.
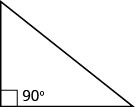
Un triángulo rectángulo tiene un ángulo de 90°, que a menudo se marca con un cuadrado en el vértice.
Un ángulo de un triángulo rectángulo mide 28°. ¿Cuál es la medida del tercer ángulo?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. | 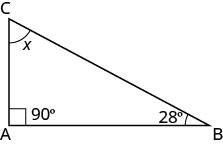 |
| Paso 2. Identifica lo que buscas. | la medida de un ángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja quex= la medida de un ángulo. |
| Paso 4. Traducir. | m∠A+m∠B+m∠C=180 |
| Escribir la fórmula apropiada y sustituirla. | x+90+28=180 |
| Paso 5. Resuelve la ecuación. | x=62 |
| Paso 6. Cheque. 180?=90+28+62180=180✓ |
|
| Paso 7. Contesta la pregunta. | La medida del tercer ángulo es de 62 °. |
Un ángulo de un triángulo rectángulo mide 56°. ¿Cuál es la medida del otro ángulo pequeño?
- Responder
-
34°
Un ángulo de un triángulo rectángulo mide 45°. ¿Cuál es la medida del otro ángulo pequeño?
- Responder
-
45°
En los ejemplos que hemos visto hasta ahora, podríamos dibujar una figura y etiquetarla directamente después de leer el problema. En el siguiente ejemplo, tendremos que definir un ángulo en términos de otro. Esperaremos a dibujar la figura hasta que escribamos expresiones para todos los ángulos que estamos buscando.
La medida de un ángulo de un triángulo rectángulo es 20 grados más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | las medidas de los tres ángulos |
| Paso 3. Nombre. Elija una variable para representarla. | Dejara=1st ángulo. a+20=2ndángulo 90=3rd de ángulo (el ángulo recto) |
| Dibuja la figura y etiquétela con la información dada | 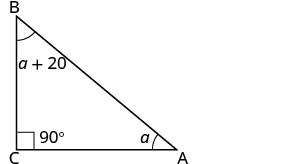 |
| Paso 4. Traducir | 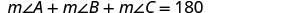 |
| Escriba la fórmula apropiada. Sustituir en la fórmula. |
a+(a+20)+90=180 |
| Paso 5. Resuelve la ecuación. |
\ (\ begin {align*} 2a + 110 &= 180\\ [3pt] |
| Paso 6. Cheque. 35+55+90?=180180=180✓ |
|
| Paso 7. Contesta la pregunta. | Los tres ángulos miden 35 °, 55 ° y 90 °. |
La medida de un ángulo de un triángulo rectángulo es 50° más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Responder
-
20°,70°,90°
La medida de un ángulo de un triángulo rectángulo es 30° más que la medida del ángulo más pequeño. Encuentra las medidas de los tres ángulos.
- Responder
-
30°,60°,90°
Usa el Teorema de Pitágoras
Hemos aprendido cómo las medidas de los ángulos de un triángulo se relacionan entre sí. Ahora, aprenderemos cómo las longitudes de los lados se relacionan entre sí. Una propiedad importante que describe la relación entre las longitudes de los tres lados de un triángulo rectángulo se llama Teorema de Pitágoras. Este teorema se ha utilizado en todo el mundo desde la antigüedad. Lleva el nombre del filósofo y matemático griego, Pitágoras, que vivió alrededor del 500 a.C.
Antes de exponer el Teorema de Pitágoras, necesitamos introducir algunos términos para los lados de un triángulo. Recuerda que un triángulo rectángulo tiene un ángulo de 90°, marcado con un pequeño cuadrado en la esquina. El lado del triángulo opuesto al ángulo de 90°90° se llama hipotenusa y cada uno de los otros lados se llama patas.
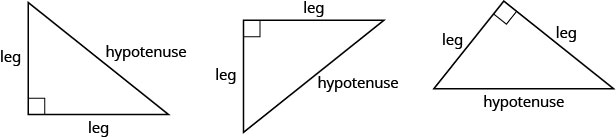
El Teorema de Pitágoras cuenta cómo las longitudes de los tres lados de un triángulo rectángulo se relacionan entre sí. Afirma que en cualquier triángulo rectángulo, la suma de los cuadrados de las longitudes de las dos patas es igual al cuadrado de la longitud de la hipotenusa. En símbolos decimos: en cualquier triángulo rectángulo,a2+b2=c2, donde a y b son las longitudes de las piernas y cc es la longitud de la hipotenusa.
Escribir la fórmula en cada ejercicio y decirlo en voz alta mientras la escribes, puede ayudarte a recordar el Teorema de Pitágoras.
En cualquier triángulo rectángulo, dondea yb son las longitudes de las piernas,c está la longitud de la hipotenusa.
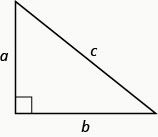
Entonces
a2+b2=c2
Para resolver ejercicios que utilicen el Teorema de Pitágoras (Ecuación\ ref {Pteorema}), necesitaremos encontrar raíces cuadradas. Hemos utilizado la notación√m y la definición:
Sim=n2, entonces√m=n, paran≥0.
Por ejemplo, encontramos que√25 es 5 porque25=52.
Debido a que el Teorema de Pitágoras contiene variables que son cuadradas, para resolver por la longitud de un lado en un triángulo rectángulo, tendremos que usar raíces cuadradas.
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa que se muestra a continuación.
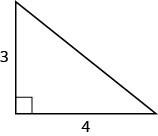
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | la longitud de la hipotenusa del triángulo |
| Paso 3. Nombre. Elija una variable para representarla. Etiqueta lado c en la figura. |
Dejar c = la longitud de la hipotenusa. 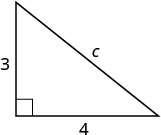 |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. | a2+b2=c2 |
| Sustituto. | 32+42=c2 |
| Paso 5. Resuelve la ecuación. | 9+16=c2 |
| Simplificar. | 25=c2 |
| Usa la definición de raíz cuadrada. | √25=c |
| Simplificar. | 5=c |
Paso 6. Cheque. 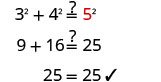 |
|
| Paso 7. Contesta la pregunta. | La longitud de la hipotenusa es de 5. |
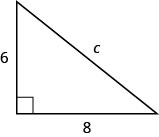
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa en el triángulo que se muestra a continuación.
- Responder
-
c=10
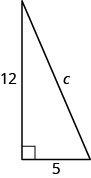
Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa en el triángulo que se muestra a continuación.
- Responder
-
c=13
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna que se muestra a continuación.
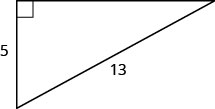
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | la longitud de la pata del triángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja queb= la pierna del triángulo. |
| Lado de la etiquetab. | 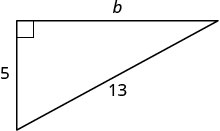 |
| Paso 4. Traducir | |
| Escriba la fórmula apropiada. | a2+b2=c2 |
| Sustituto. | 52+b2=132 |
| Paso 5. Resuelve la ecuación. |
25+b2=169 |
| Aísle el término variable. | b2=144 |
| Usa la definición de raíz cuadrada. | b=√144 |
| Simplificar. | b=12 |
Paso 6. Cheque. 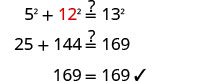 |
|
| Paso 7. Contesta la pregunta. | La longitud de la pierna es de 12. |
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna en el triángulo que se muestra a continuación.
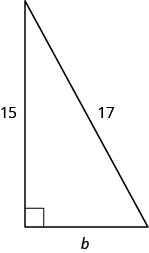
- Responder
-
8
Usa el Teorema de Pitágoras para encontrar la longitud de la pierna en el triángulo que se muestra a continuación.
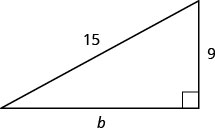
- Contestar
-
12
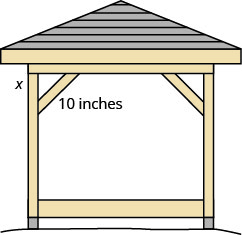
Kelvin está construyendo una glorieta y quiere encordar cada esquina colocando una pieza de madera de 10″ en diagonal como se muestra arriba.
Si sujeta la madera para que los extremos del corsé estén a la misma distancia de la esquina, ¿cuál es la longitud de las patas del triángulo rectángulo formado? Aproximado a la décima de pulgada más cercana.
Solución
Step 1. Read the problem.Step 2. Identify what we are looking for.the distance from the corner that thebracket should be attachedStep 3. Name. Choose a variable to represent it.Let x = distance from the corner.Step 4.TranslateWrite the appropriate formula and substitute.a2+b2=c2x2+x2=102Step 5. Solve the equation.2x2=100Isolate the variable.x2=50Simplify. Approximate to the nearest tenth.x≈7.1Step 6. Check.a2+b2=c2(7.1)2+(7.1)2≈102 Yes.Step 7. Answer the question.Kelven should fasten each piece ofwood approximately 7.1'' from the corner.
John pone la base de una escalera de 13 pies a cinco pies de la pared de su casa como se muestra a continuación. ¿A qué distancia de la pared llega la escalera?

- Contestar
-
12 pies
Randy quiere unir una cadena de luces de 17 pies a la parte superior del mástil de 15 pies de su velero, como se muestra a continuación. ¿A qué distancia de la base del mástil debe sujetar el extremo de la cuerda de luz?
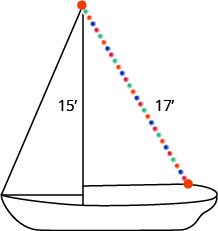
- Contestar
-
8 pies
Resolver aplicaciones usando propiedades de rectángulo
Es posible que ya estés familiarizado con las propiedades de los rectángulos. Los rectángulos tienen cuatro lados y cuatro ángulos rectos (90°). Los lados opuestos de un rectángulo tienen la misma longitud. Nos referimos a un lado del rectángulo como la longitud,L, y su lado adyacente como el ancho,W.
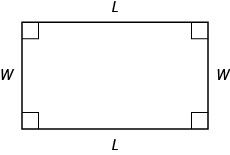
La distancia alrededor de este rectángulo esL+W+L+W, o2L+2W. Este es el perímetroP,, del rectángulo.
P=2L+2W
¿Qué pasa con el área de un rectángulo? Imagina una alfombra rectangular que mide 2 pies de largo por 3 pies de ancho. Su área es de 6 pies cuadrados. Hay seis cuadrados en la figura.
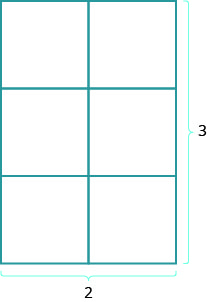
A=6A=2⋅3A=L⋅W
El área es la longitud por el ancho. La fórmula para el área de un rectángulo es
A=LW.
Los rectángulos tienen cuatro lados y cuatro ángulos rectos (90°).
Las longitudes de lados opuestos son iguales.
El perímetro de un rectángulo es la suma del doble de la longitud y del doble de la anchura.
P=2L+2W
El área de un rectángulo es el producto de la longitud y la anchura.
A=L·W
La longitud de un rectángulo es de 32 metros y el ancho es de 20 metros. ¿Cuál es el perímetro?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. |
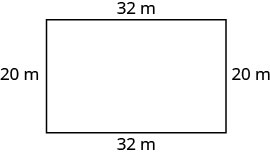 |
| Paso 2. Identifica lo que buscas. | el perímetro de un rectángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja queP= el perímetro. |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. |  |
| Sustituto. | 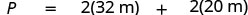 |
| Paso 5. Resuelve la ecuación. | P=64+40 P=104 |
| Paso 6. Cheque. P?=10420+32+20+32?=104104=104✓ |
|
| Paso 7. Contesta la pregunta. | El perímetro del rectángulo es de 104 metros. |
La longitud de un rectángulo es de 120 yardas y el ancho es de 50 yardas. ¿Cuál es el perímetro?
- Contestar
-
340 yardas
La longitud de un rectángulo es de 62 pies y el ancho es de 48 pies. ¿Cuál es el perímetro?
- Contestar
-
220 pies
El área de una habitación rectangular es de 168 pies cuadrados. La longitud es de 14 pies. ¿Cuál es el ancho?
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. |
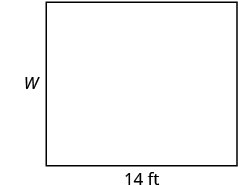 |
| Paso 2. Identifica lo que buscas. | el ancho de una habitación rectangular |
| Paso 3. Nombre. Elija una variable para representarla. | Deja queW= el ancho. |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. | A=LW |
| Sustituto. | 168=14W |
| Paso 5. Resuelve la ecuación. |
16814=14W14 12=W |
Paso 6. Cheque.  A=LW168?=14⋅12168=168✓ |
|
| Paso 7. Contesta la pregunta. | El ancho de la habitación es de 12 pies. |
El área de un rectángulo es de 598 pies cuadrados. La longitud es de 23 pies. ¿Cuál es el ancho?
- Contestar
-
26 pies
El ancho de un rectángulo es de 21 metros. El área es de 609 metros cuadrados. ¿Cuál es la longitud?
- Contestar
-
29 metros
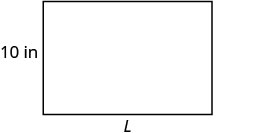
Encuentra la longitud de un rectángulo con perímetro de 50 pulgadas y ancho 10 pulgadas.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. |
  |
| Paso 2. Identifica lo que buscas. | la longitud del rectángulo |
| Paso 3. Nombre. Elija una variable para representarla. | Deja queL= la longitud. |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. | P=2L+2W |
| Sustituto. | 50=2L+2(10) |
| Paso 5. Resuelve la ecuación. | 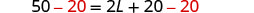 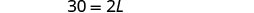 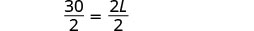  |
Paso 6. Cheque.  P=5015+10+15+10?=5050=50✓ |
|
| Paso 7. Contesta la pregunta. | La longitud es de 15 pulgadas. |
Encuentra la longitud de un rectángulo con: perímetro 80 y ancho 25.
- Contestar
-
15
Encuentra la longitud de un rectángulo con: perímetro 30 y ancho 6.
- Contestar
-
9
Hemos resuelto problemas donde se dio el largo o el ancho, junto con el perímetro o área; ahora aprenderemos a resolver problemas en los que se define el ancho en términos de la longitud. Esperaremos a dibujar la figura hasta que escribamos una expresión para el ancho para que podamos etiquetar un lado con esa expresión.
El ancho de un rectángulo es dos pies menos que la longitud. El perímetro es de 52 pies. Encuentra el largo y ancho.
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | el largo y ancho de un rectángulo |
| Paso 3. Nombre. Elija una variable para representarla. Dado que el ancho se define en términos de la longitud, dejamos que laL= longitud. El ancho es dos pies menos que el largo, así que dejamosL−2 ancho. |
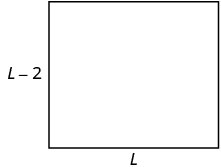 P=52ft |
| Paso 4. Traducir. | |
| Escriba la fórmula apropiada. La fórmula para el perímetro de un rectángulo relaciona toda la información. | P=2L+2W |
| Sustituir en la información dada. | 52=2L+2(L−2) |
| Paso 5. Resuelve la ecuación. | 52=2L+2L−4 |
| Combina términos similares. | 52=4L−4 |
| Agrega 4 a cada lado. | 56=4L |
| Dividir por 4. | 564=4L4 14=L La longitud es de 14 pies. |
| Ahora necesitamos encontrar el ancho. | El ancho esL−2.  El ancho es de 12 pies. |
| Paso 6. Cheque. Ya que14+12+14+12=52, ¡esto funciona!  |
|
| Paso 7. Contesta la pregunta. | La longitud es de 14 pies y el ancho es de 12 pies. |
El ancho de un rectángulo es siete metros menos que la longitud. El perímetro es de 58 metros. Encuentra el largo y ancho.
- Contestar
-
18 metros, 11 metros
La longitud de un rectángulo es ocho pies más que el ancho. El perímetro es de 60 pies. Encuentra el largo y ancho.
- Contestar
-
19 pies, 11 pies
La longitud de un rectángulo es de cuatro centímetros más del doble del ancho. El perímetro es de 32 centímetros. Encuentra el largo y ancho.
Solución
| Paso 1. Lee el problema. | |
| Paso 2. Identifica lo que buscas. | el largo y el ancho |
| Paso 3. Nombre. Elija una variable para representar el ancho. |  |
| El largo es de cuatro más del doble de ancho. | 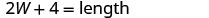 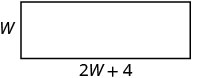 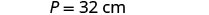 |
| Paso 4. Traducir | |
| Escriba la fórmula apropiada. | P=2L+2W |
| Sustituir en la información dada. | 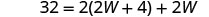 |
| Paso 5. Resuelve la ecuación. | 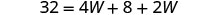 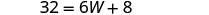 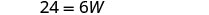 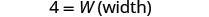 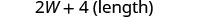  12 La longitud es 12 cm. |
Paso 6. Cheque. 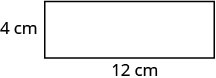 P=2L+2W32?=2⋅12+2⋅432=32✓ |
|
| Paso 7. Contesta la pregunta. | El largo es de 12 cm y el ancho es de 4 cm. |
La longitud de un rectángulo es ocho más del doble del ancho. El perímetro es de 64. Encuentra el largo y ancho.
- Contestar
-
24, 8
El ancho de un rectángulo es seis menos del doble de la longitud. El perímetro es 18. Encuentra el largo y ancho.
- Contestar
-
5, 4
El perímetro de una piscina rectangular es de 150 pies. La longitud es de 15 pies más que el ancho. Encuentra el largo y ancho.
Solución
| Paso 1. Lee el problema. Dibuja la figura y etiquétela con la información dada. |
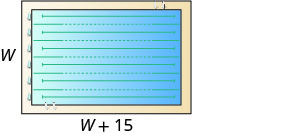 P=150ft |
| Paso 2. Identifica lo que buscas. | la longitud y el ancho de la piscina |
| Paso 3. Nombre. Elija una variable para representar el ancho. La longitud es de 15 pies más que el ancho. |
 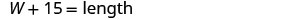 |
| Paso 4. Traducir | |
| Escriba la fórmula apropiada. | P=2L+2W |
| Sustituto. | 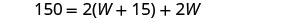 |
| Paso 5. Resuelve la ecuación. | 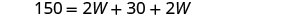 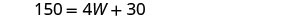      |
| Paso 6. Cheque. P=2L+2W150?=2(45)+2(30)150=150✓ |
|
| Paso 7. Contesta la pregunta. | La longitud de la piscina es de 45 pies y el ancho es de 30 pies. |
El perímetro de una piscina rectangular es de 200 pies. El largo es 40 pies más que el ancho. Encuentra el largo y ancho.
- Contestar
-
70 pies, 30 pies
La longitud de un jardín rectangular es de 30 yardas más que el ancho. El perímetro es de 300 yardas. Encuentra el largo y ancho.
- Contestar
-
90 yardas, 60 yardas
Conceptos clave
- Estrategia de resolución de problemas para aplicaciones de geometría
- Lee el problema y haz que se entiendan todas las palabras e ideas. Dibuja la figura y etiquétela con la información dada.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando eligiendo una variable para representarlo.
- Traduzca en una ecuación escribiendo la fórmula o modelo apropiado para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
- Propiedades del triángulo Para las medidas del
ángulo de D ABC:- m∠A+m∠B+m∠C=180
- P=a+b+c
- A=12bh, b=base, h=altura
- El teorema de Pitágoras En cualquier triángulo rectángulo,a2+b2=c2 dondec está la longitud de la hipotenusaa y yb son las longitudes de las piernas.
- Propiedades de Rectángulos
- Los rectángulos tienen cuatro lados y cuatro ángulos rectos (90°).
- Las longitudes de lados opuestos son iguales.
- El perímetro de un rectángulo es la suma del doble de la longitud y del doble de la anchura:P=2L+2W.
- El área de un rectángulo es la longitud por el ancho:A=LW.


