3.1: Paralelogramos
- Page ID
- 114651
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Un polígono es una figura formada por segmentos de línea que delimitan una parte del plano (Figura\(\PageIndex{1}\)), Los segmentos de línea delimitadora se denominan los lados del polígono, Los ángulos formados por los lados son los ángulos del polígono y los vértices de estos ángulos son los vértices del polígono, El polígono más simple es el triángulo, que tiene 3 lados, En este capítulo estudiaremos el cuadrilátero, el polígono con 4 lados (Figura\(\PageIndex{2}\)). Otros polígonos son el pentágono (5 lados), el hexágono (6 lados), el octágono (8 lados) y el decágono (10 lados).
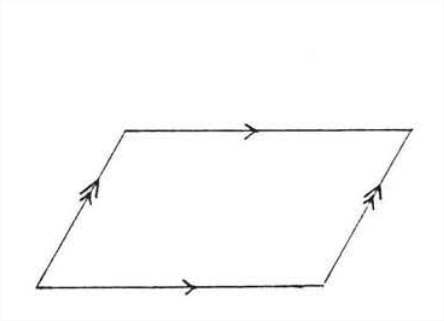
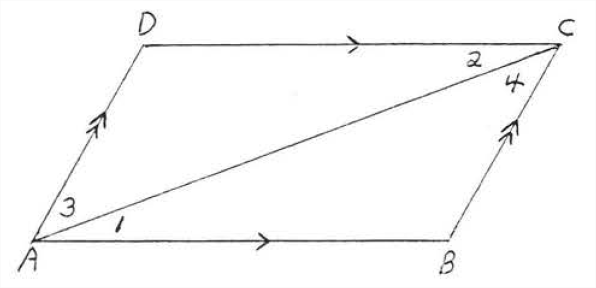
Un paralelogramo es un cuadrilátero en el que los lados opuestos son paralelos (Figura\(\PageIndex{3}\)). Para descubrir sus propiedades, dibujaremos una diagonal, una línea que conecta los vértices opuestos del paralelogramo. En la Figura 4, AC es una diagonal de paralelogramo\(ABCD\). Ahora vamos a probar\(\Delta ABC \cong \Delta CDA\).
| Declaraciones | Razones |
|---|---|
| 1. \(\angle 1 = \angle 2\). | 1. Los ángulos interiores alternos de líneas paralelas\(AB\) y\(CD\) son iguales. |
| 2. \(\angle 3 = \angle 4\). | 2. Los ángulos interiores alternos de líneas paralelas\(BC\) y\(AD\) son iguales. |
| 3. \(AC = AC\). | 3. Identidad. |
| 4. \(\triangle ABC \cong \triangle CDA\). | 4. \(ASA = ASA\). |
| 5. \(AB = CD\),\(BC = DA\). | 5. Los lados correspondientes de los triángulos congruentes son iguales. |
| 6. \(\angle B = \angle D\). | 6. Los ángulos correspondientes de los triángulos congruentes son iguales. |
| 7. \(\angle A = \angle C\). | 7. \(\angle A = \angle 1 +\angle 3 = \angle 2 + \angle 4 = \angle C\)(Añádese los estados 1 y 2). |
Hemos demostrado el siguiente teorema:
Los lados opuestos y los ángulos opuestos de un paralelogramo son iguales.
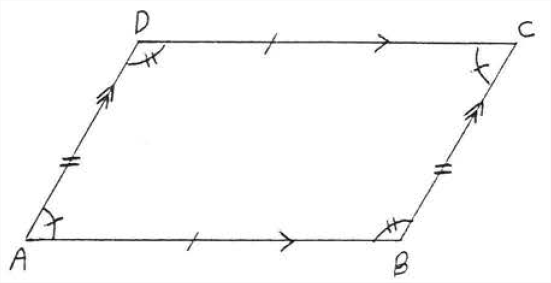
En paralelogramo\(ABCD\) de la Figura\(\PageIndex{5}\),\(AB = CD\),\(AD = BC\),\(\angle A = \angle C\), y\(\angle B = \angle D\).
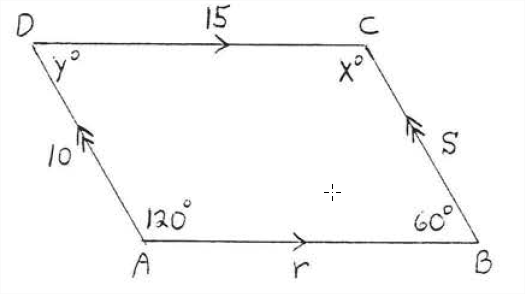
Buscar\(x\),\(y\),\(r\) y\(s\):
Solución
Por teorema\(\PageIndex{1}\), los lados opuestos y los ángulos opuestos son iguales. De ahí\(x^{\circ} = 120^{\circ}\),\(y^{\circ} = 60^{\circ}, r = 15\), y\(s = 10\).
Respuesta:\(x = 120, y = 60, r = 15, s = 10\).
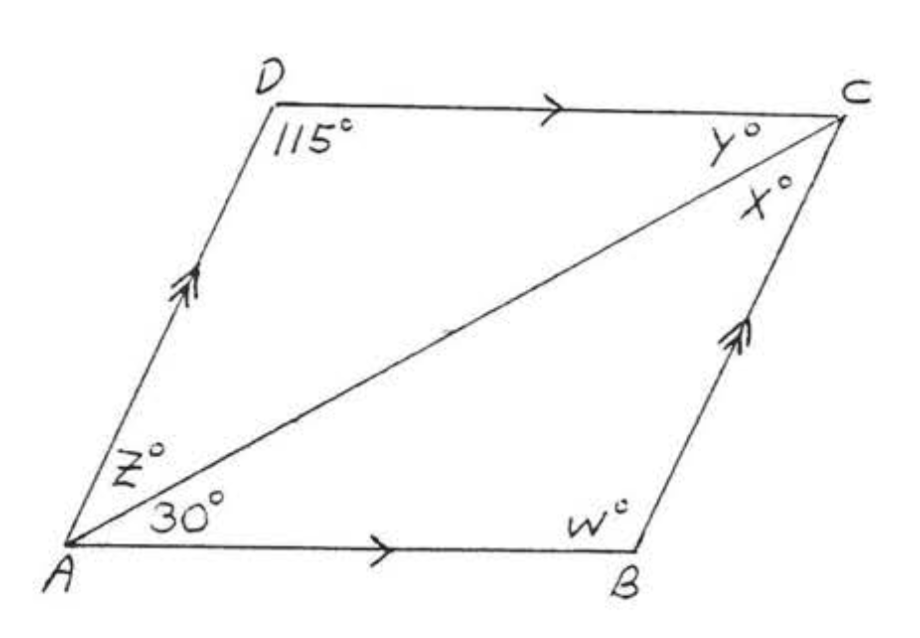
Encuentra\(x, y, x\) y\(z:\)
Solución
\(w^{\circ} = 115^{\circ}\)ya que los ángulos opuestos de un paralelogramo son iguales. \(x^{\circ} = 180^{\circ} -(w^{\circ} + 30^{\circ}) = 180^{\circ} - (115^{\circ} + 30^{\circ}) = 180^{\circ} - 145^{\circ} = 35^{\circ}\), porque la suma de los ángulos de\(\triangle ABC\) es\(180^{\circ}\),\(y^{\circ} = 30^{\circ}\) y\(x^{\circ} = x^{\circ} = 35^{\circ}\) porque son ángulos interiores alternos de líneas paralelas.
Respuesta:\(w = 115\),\(x = z = 35\),\(y = 30\).
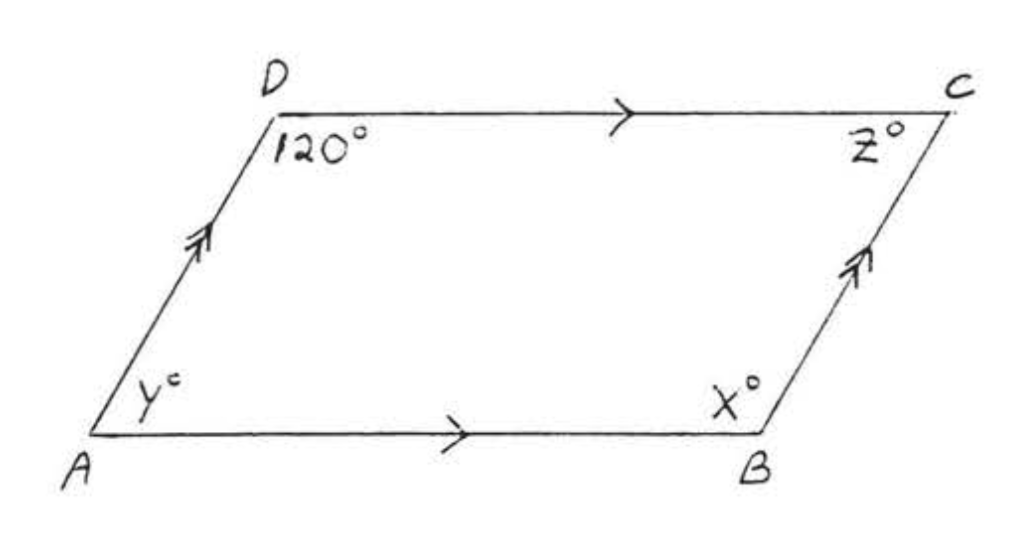
Buscar\(x\),\(y\), y\(z\):
Solución
\(x = 120\)y\(y = z\) porque los ángulos opuestos son iguales,\(\angle A\) y\(\angle D\) son J suplementarios porque son ángulos interiores en el mismo lado de la transversal de líneas paralelas (forman la letra “C” Teorema\(\PageIndex{3}\), sección 1.4).
Respuesta:\(x = 120, y = z = 60\).
En Ejemplo\(\PageIndex{3}\),\(\angle A\) y\(\angle B\),\(\angle B\) y\(\angle C\),\(\angle C\) y\(\angle D\), y\(\angle D\) y\(\angle A\) se denominan los ángulos sucesivos de paralelogramo\(ABCD\). Ejemplo\(\PageIndex{3}\) sugiere el siguiente teorema:
Los ángulos sucesivos de un paralelogramo son suplementarios.
En la Figura 6,\(\angle A + \angle B = \angle B + \angle C = \angle C + \angle D = \angle D + \angle A = 180^{\circ}\).
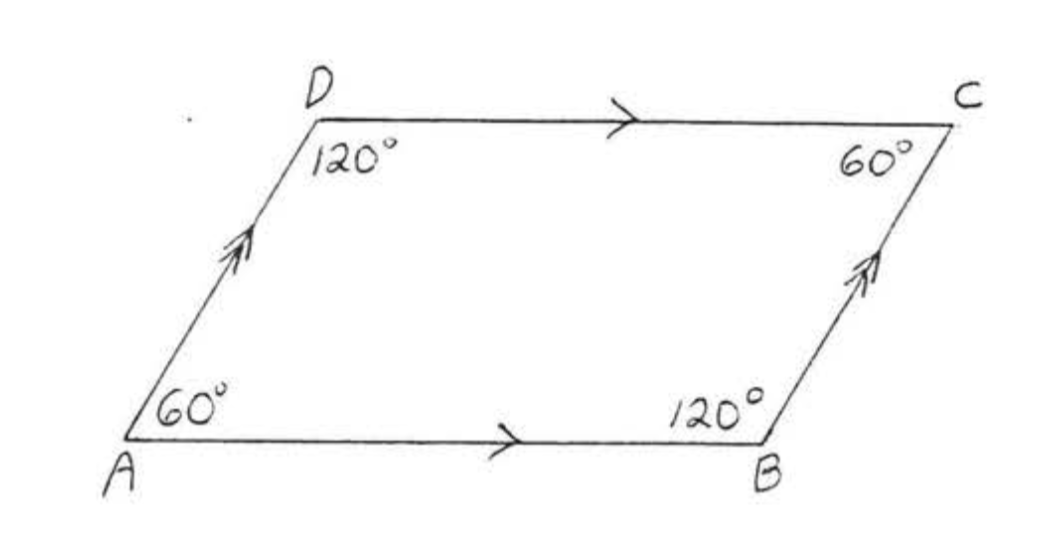
Encontrar\(x\),\(\angle A\),\(\angle B\),\(\angle C\), y\(\angle D\).
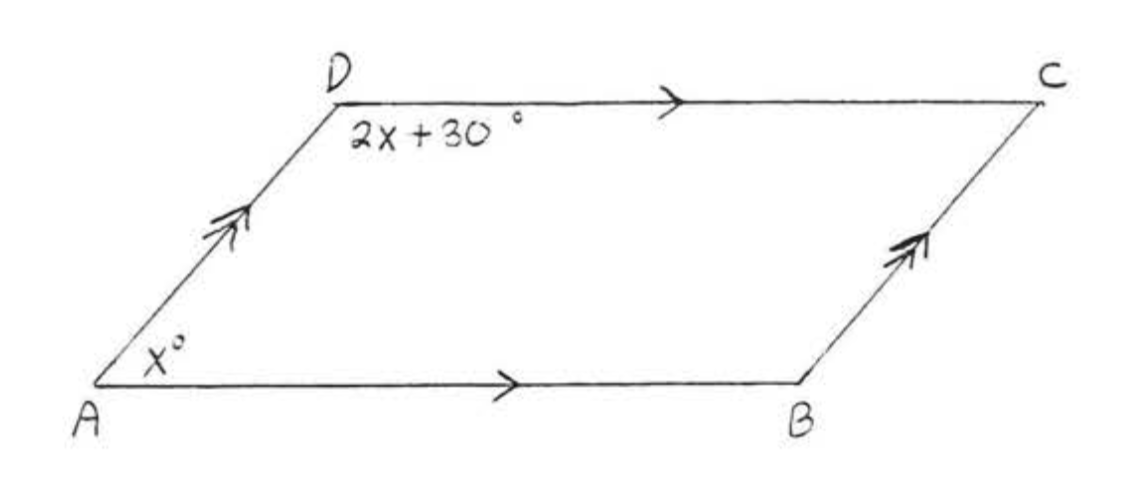
Solución
\(\angle A\)y\(\angle D\) son complementarios por Teorema\(\PageIndex{2}\).
\[\begin{array} {rcl} {\angle A + \angle D} & = & {180^{\circ}} \\ {x + 2x + 30} & = & {180} \\ {3x + 30} & = & {180} \\ {3x} & = & {180 - 30} \\ {3x} & = & {150} \\ {x} & = & {50} \end{array}\]
\(\angle A = x^{\circ} = 50^{\circ}\)
\(\angle C = \angle A = 50^{\circ}\)
\(\angle D = 2x + 30^{\circ} = 2(50) + 30^{\circ} = 100 + 30^{\circ} = 130^{\circ}\).
\(\angle B = \angle D = 130^{\circ}\).
Comprobar:
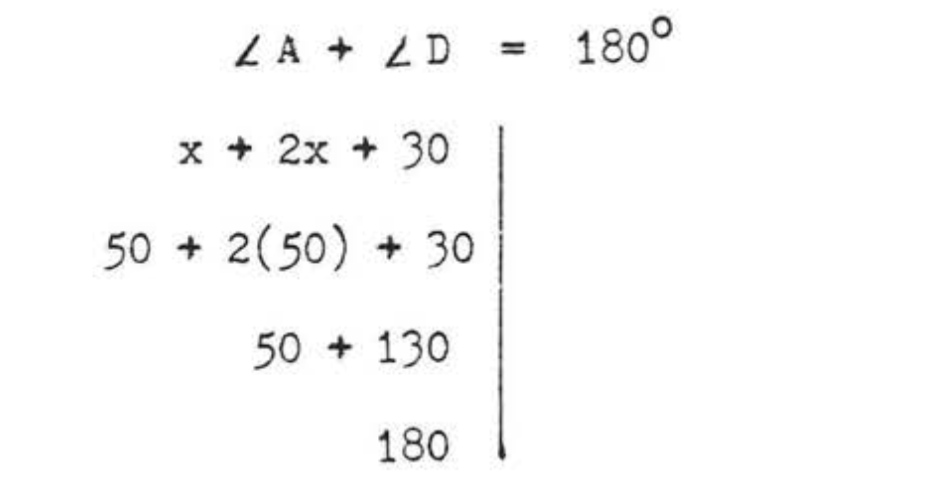
Respuesta:\(x = 50\),\(A = 50^{\circ}\),\(B = 130^{\circ}\),\(C = 50^{\circ}\),\(D = 130^{\circ}\).
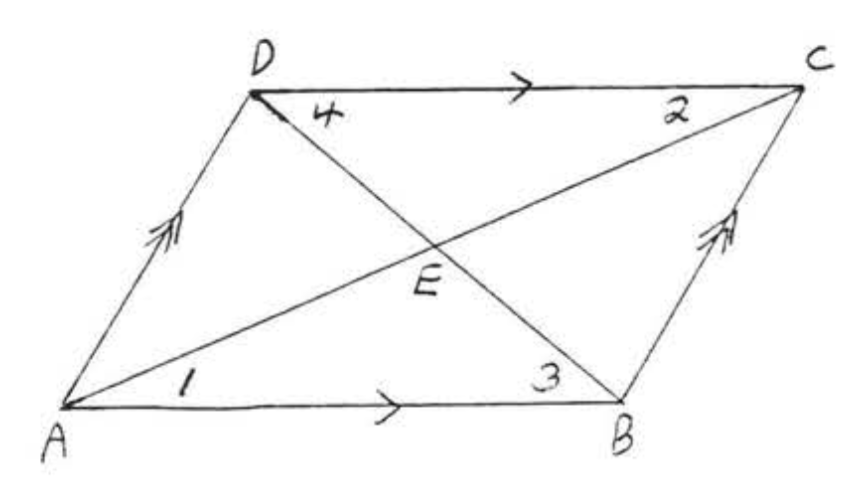
Supongamos ahora que se dibujan ambas diagonales de paralelogramo (Figura\(\PageIndex{7}\)):
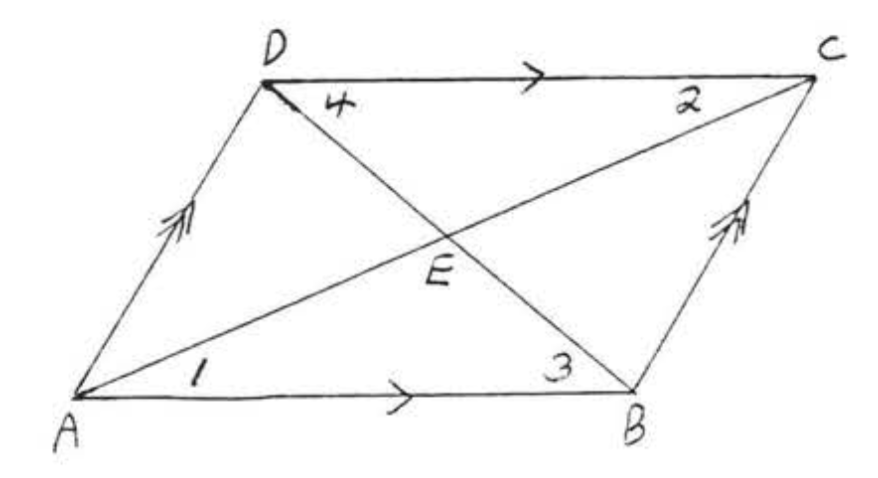
Tenemos\(\angle 1 = \angle 2\) and \(\angle 3 = \angle 4\) (both pairs of angles are alternate interior angles of parallel lines \(AB\) and \(CD\). Also \(AB = CD\) from Theorem\(\PageIndex{1}\). Therefore \(\triangle ABE \cong \triangle CDE\) by \(ASA = ASA\). Since corresponding sides of congruent triangles are equal, \(AE = CE\) and \(DE = BE\). We have proven:
Las diagonales de un paralelogramo se bisecan entre sí (se cortan entre sí por la mitad).
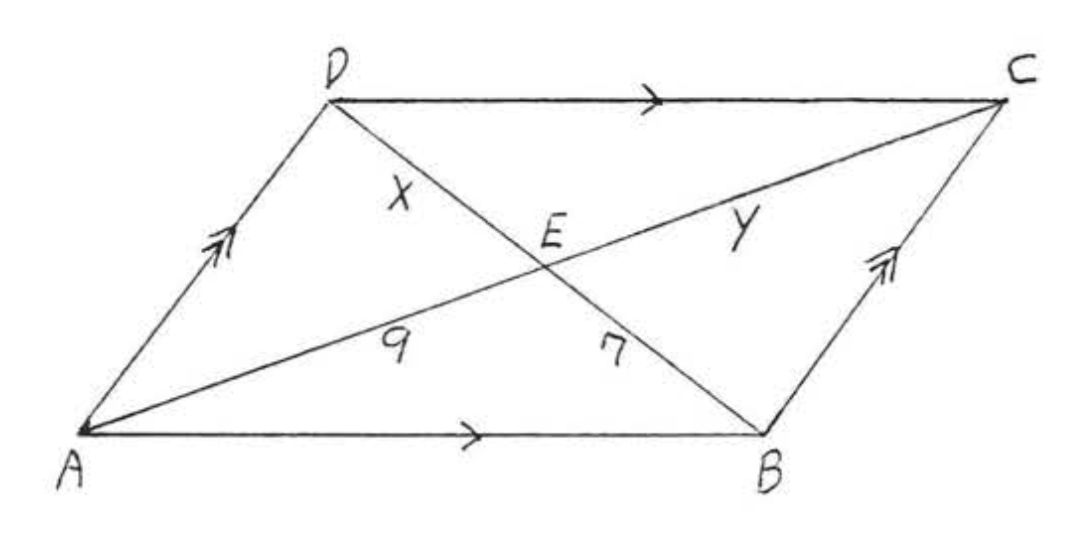
Buscar\(x, y, AC\), y\(BD\):
Solución
Por Teorema\(\PageIndex{3}\) las diagonales se bisecan entre sí.
\[\begin{array} {rcl} {x} & = & {7} \\ {y} & = & {9} \\ {AC} & = & {9 + 9 = 18} \\ {BD} & = & {7 + 7 = 14} \end{array}\]
Respuesta:\(x = 7, y = 9, AC = 18, BD = 14\).
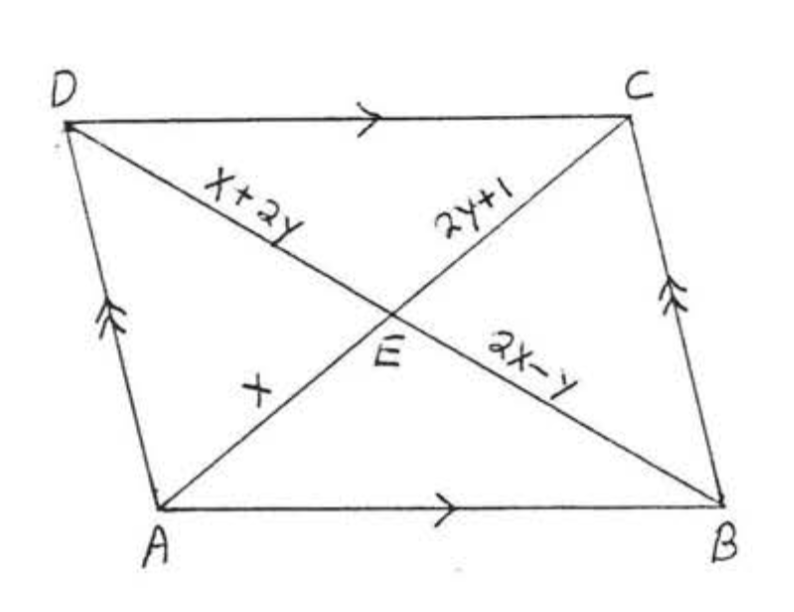
Buscar\(x, y, AC\), y\(BD\):
Solución
Por Teorema\(\PageIndex{3}\) las diagonales se bisecan entre sí.
\(\begin{array} {rcl} {AE} & = & {CE} \\ {x} & = & {2y + 1} \\ {x - 2y} & = & {1} \end{array}\)\(\begin{array} {rcl} {BE} & = & {DE} \\ {2x - y} & = & {x + 2y} \\ {2x - y - x - 2y} & = & {0} \\ {x - 3y} & = & {0} \end{array}\)
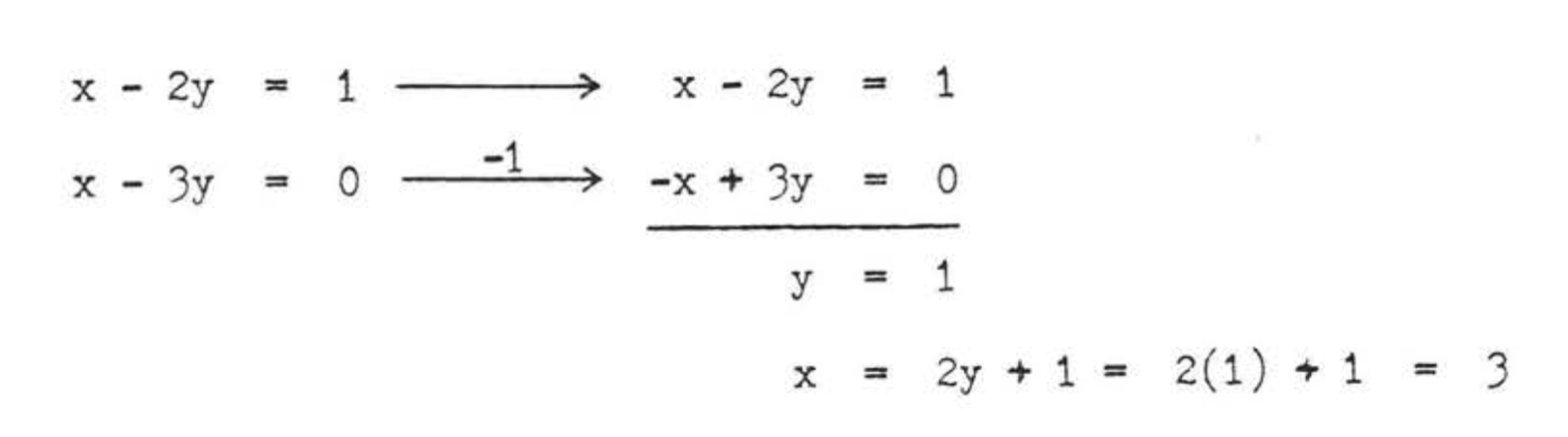
Comprobar:
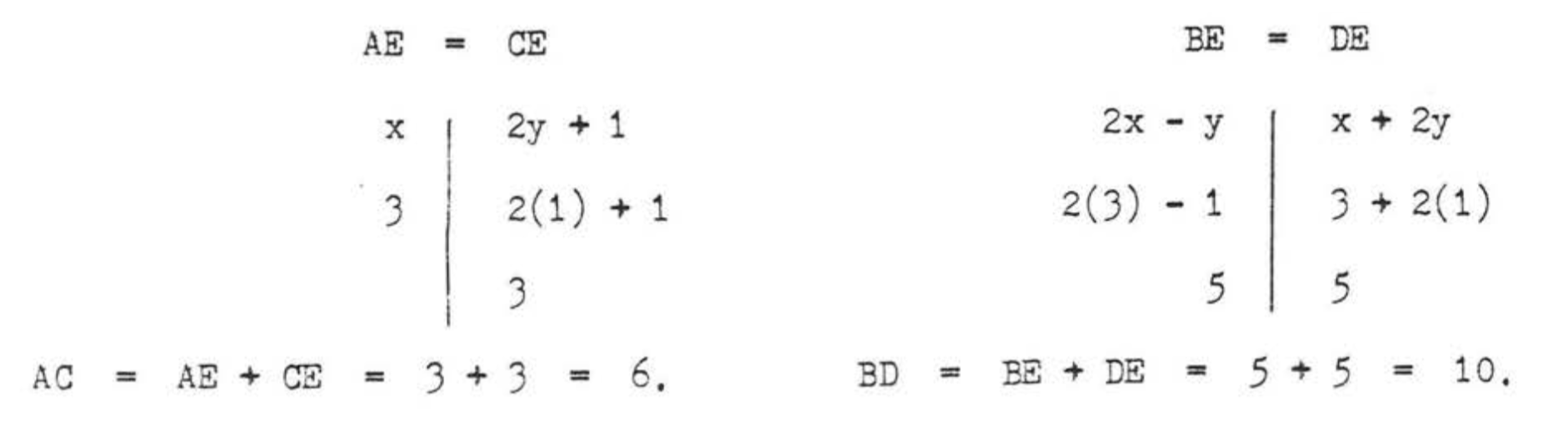
Respuesta:\(x = 3, y = 1, AC = 6, BD = 10\).
Buscar\(x, y, \angle A, \angle B, \angle C\), y\(\angle D\):
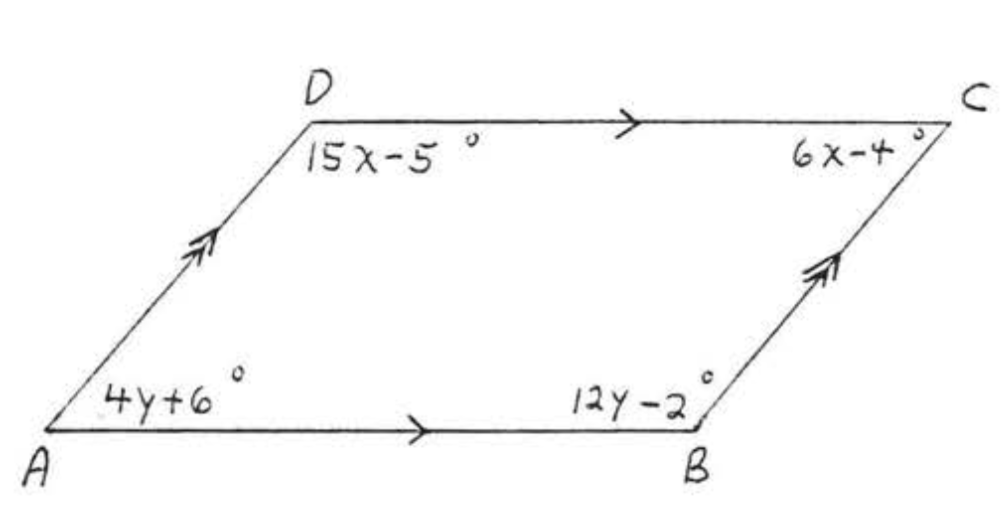
Solución
Por teorema\(\PageIndex{2}\):
\(\begin{array} {rcl} {\angle A + \angle B} & = & {180^{\circ}} \\ {4y + 6 + 12y - 2} & = & {180} \\ {16y + 4} & = & {180} \\ {16y} & = & {180 - 4} \\ {16y} & = & {176} \\ {y} & = & {11} \end{array}\)y\(\begin{array} {rcl} {\angle C + \angle D} & = & {180^{\circ}} \\ {6x - 4 + 15x - 5} & = & {180} \\ {21x - 9} & = & {180} \\ {21x} & = & {180 + 9} \\ {21x} & = & {189} \\ {x} & = & {9} \end{array}\)
Comprobar:
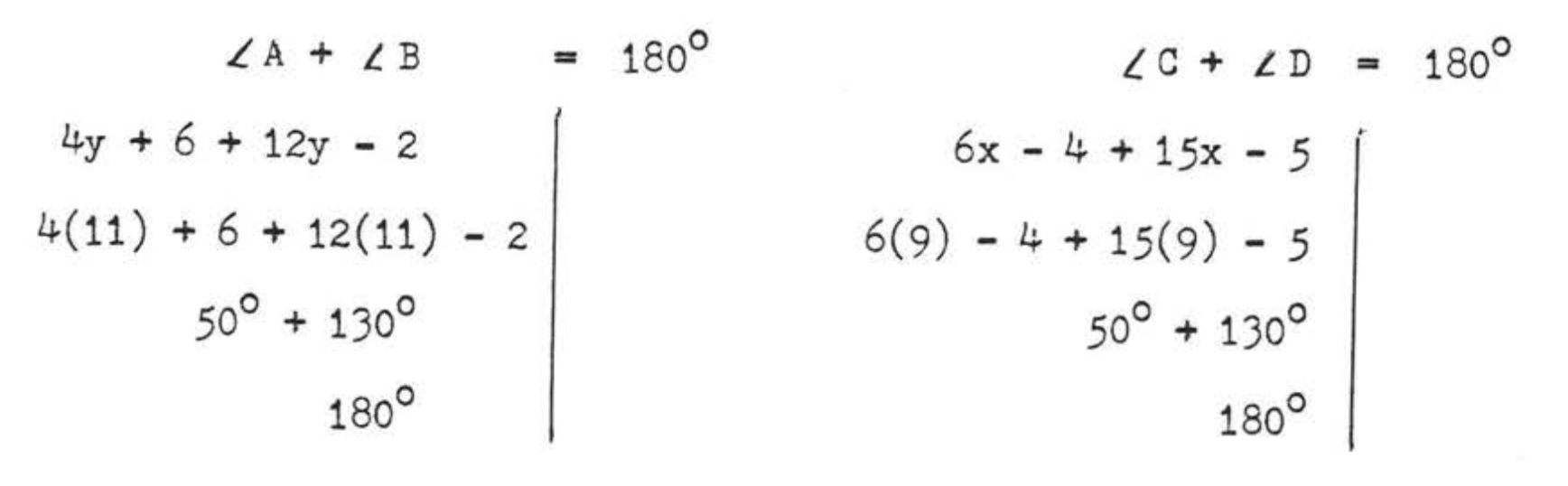
Respuesta:\(x = 9, y = 11, \angle A = \angle C = 50^{\circ}, \angle B = \angle D = 130^{\circ}\).
Problemas
Para cada uno de los siguientes estados cualquier teorema utilizado en la obtención de su (s) respuesta (s):
1. Buscar\(x, y, r\), y\(s\):
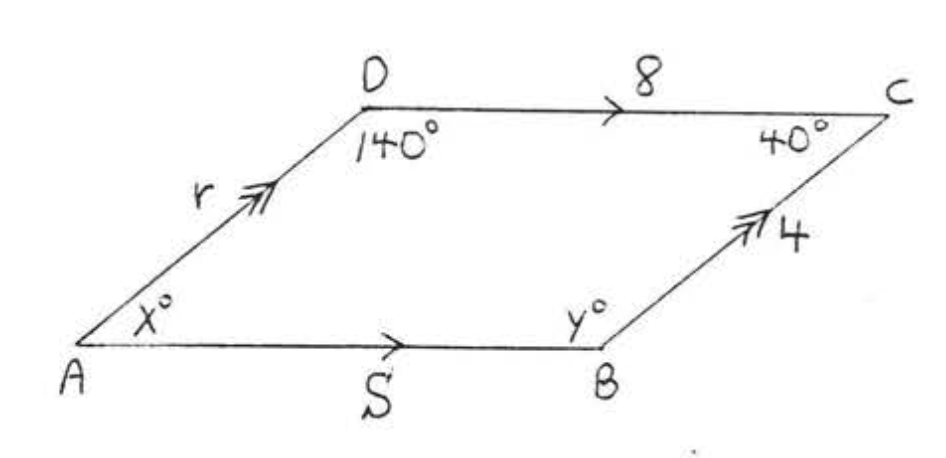
2. Buscar\(x, y, r\), y\(s\):
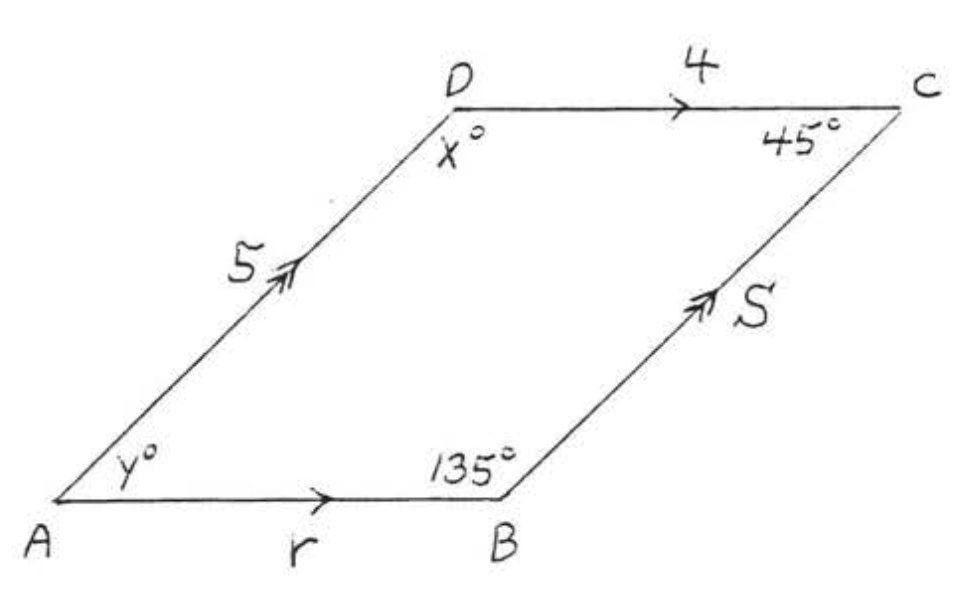
3. Buscar\(w, x, y\), y\(z\):
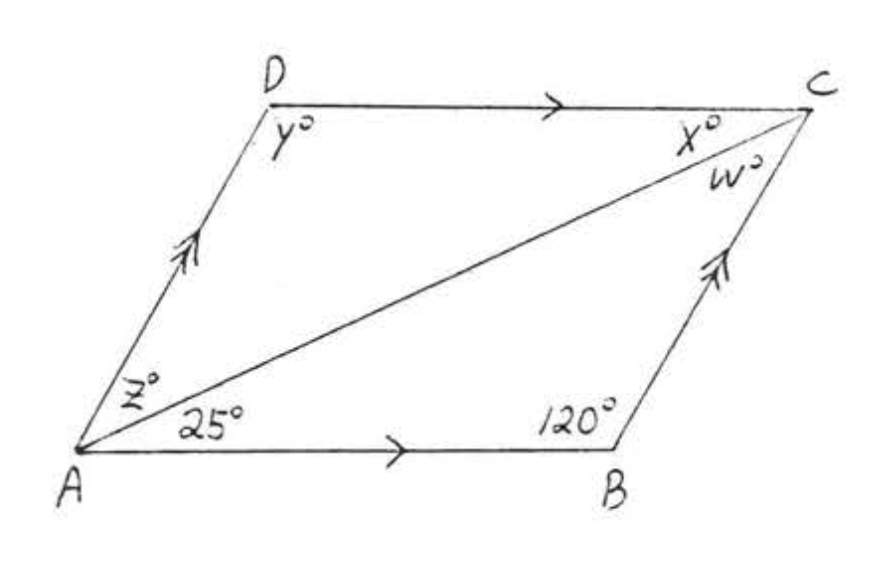
4. Buscar\(w, x, y\), y\(z\):
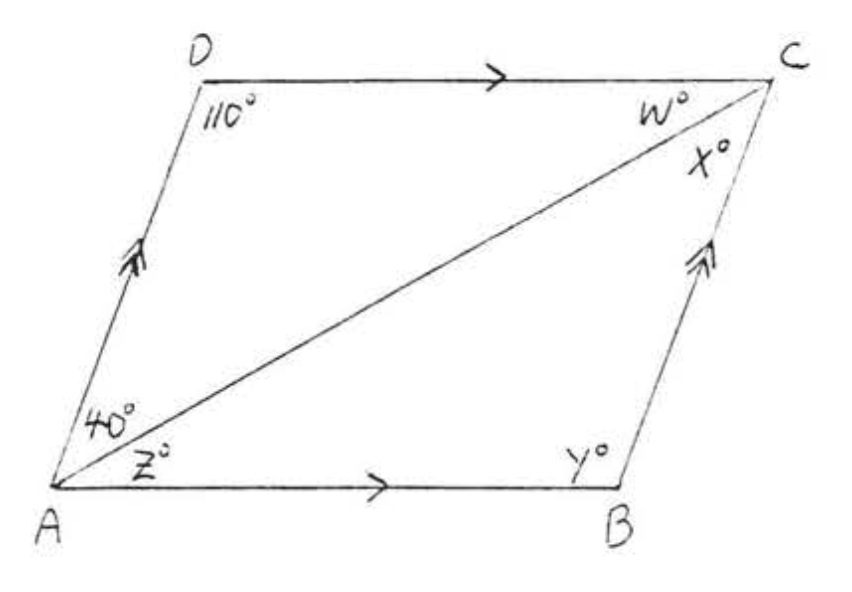
5. Buscar\(x, y\), y\(z\):
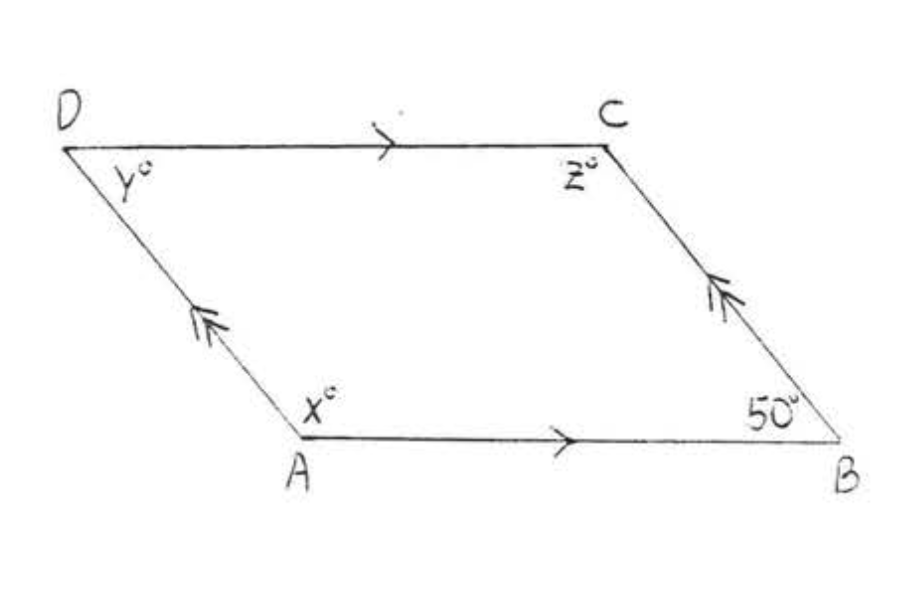
6. Buscar\(x, y\), y\(z\):
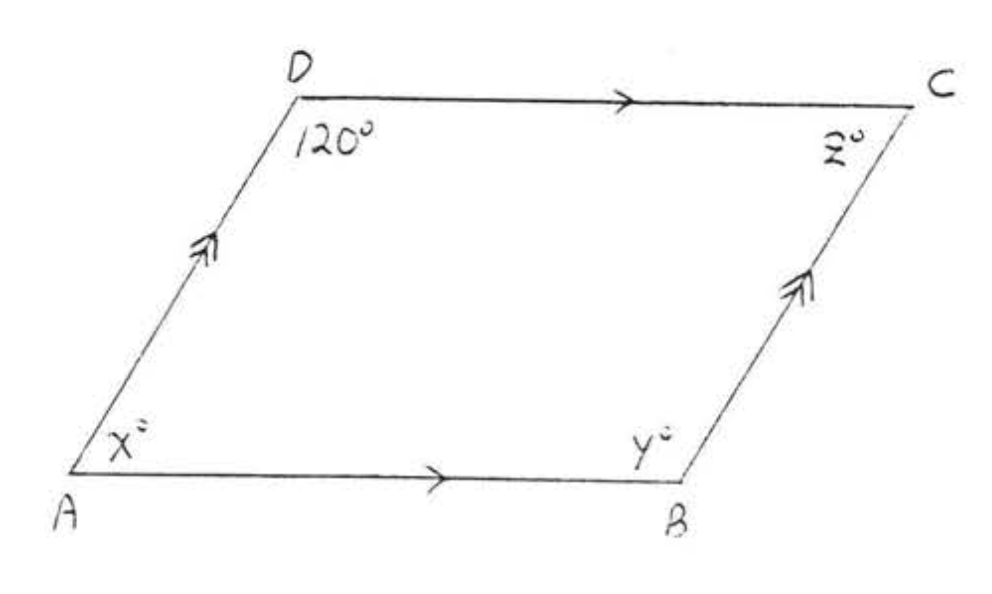
7. Buscar\(x, \angle A, \angle B, \angle C\), y\(\angle D\):
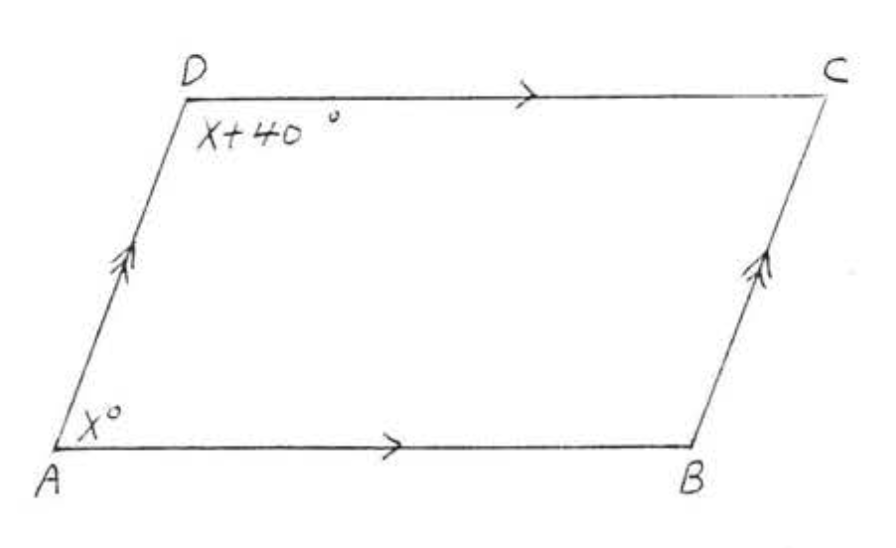
8. Buscar\(x, \angle A, \angle B, \angle C\), y\(\angle D\):
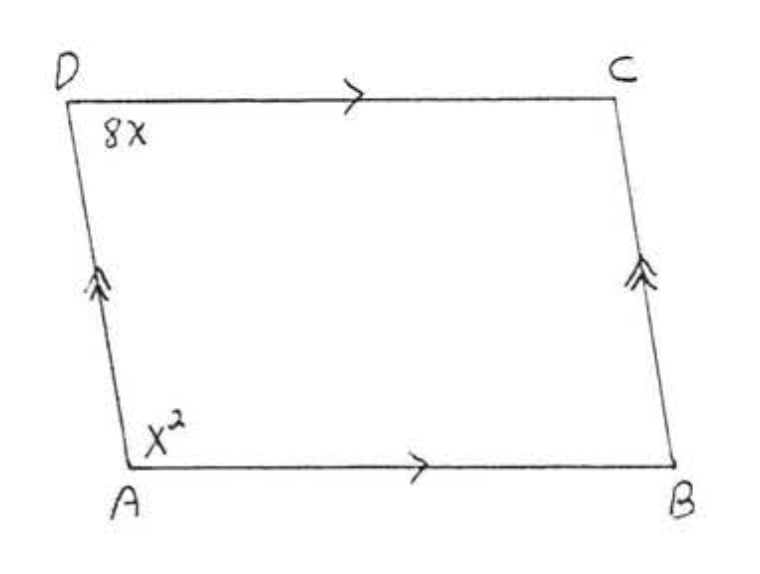
9. Buscar\(x, y, AC\), y\(BD\):
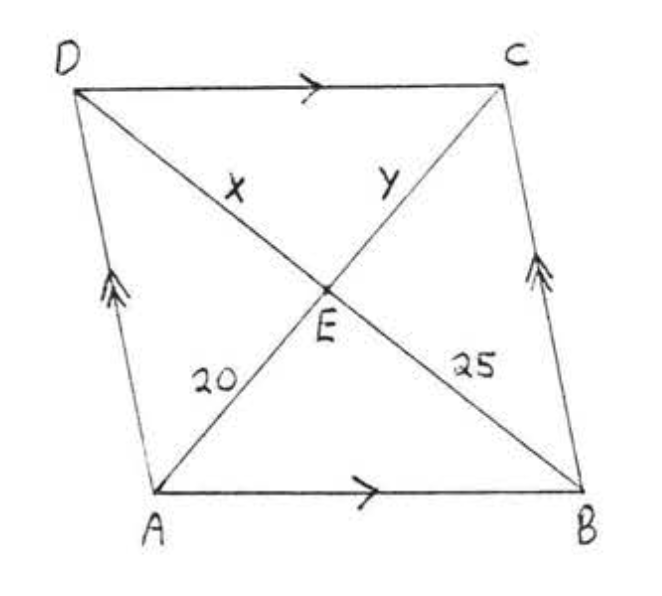
10. Buscar\(x, y, AC\), y\(BD\):
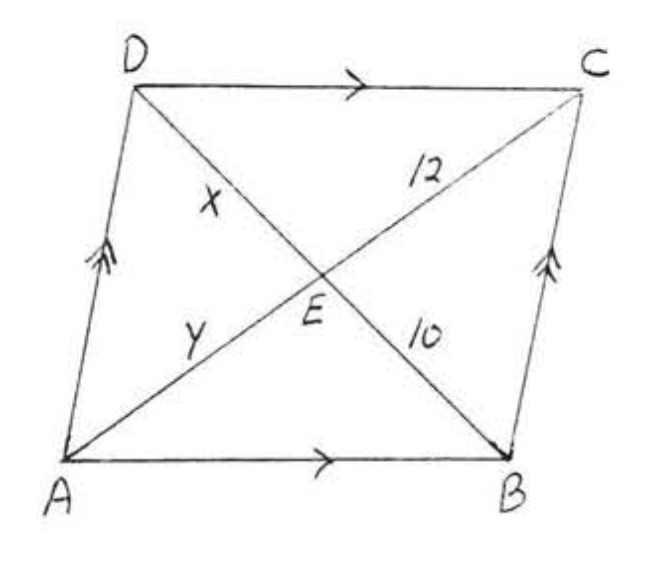
11. Buscar\(x, AB\), y\(CD\):
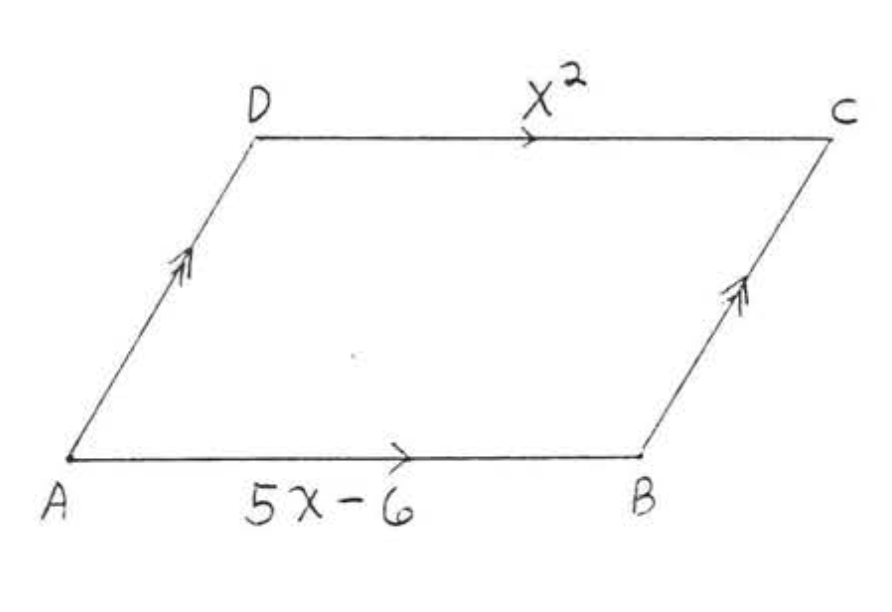
12. Buscar\(x, AD\), y\(BC\):
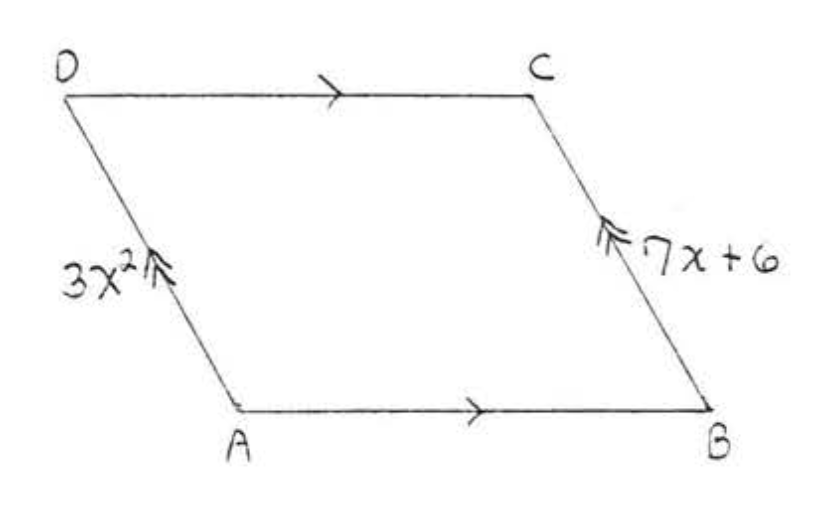
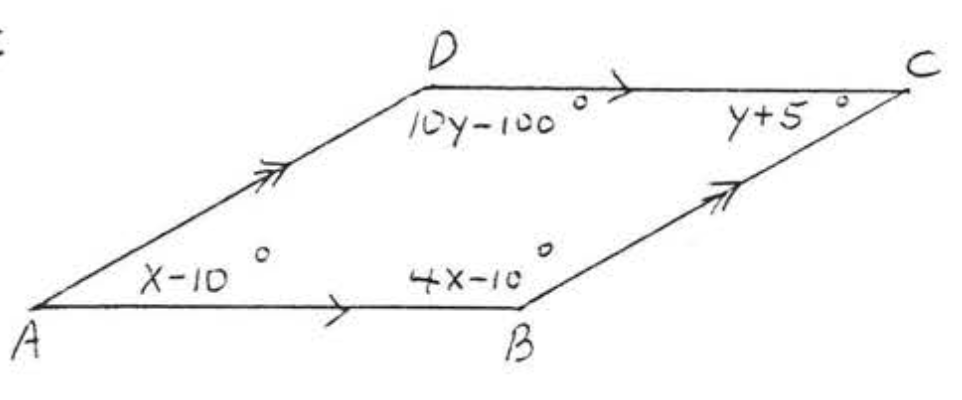
13. Buscar\(x, y, AB, BC, CD\), y\(AD\):
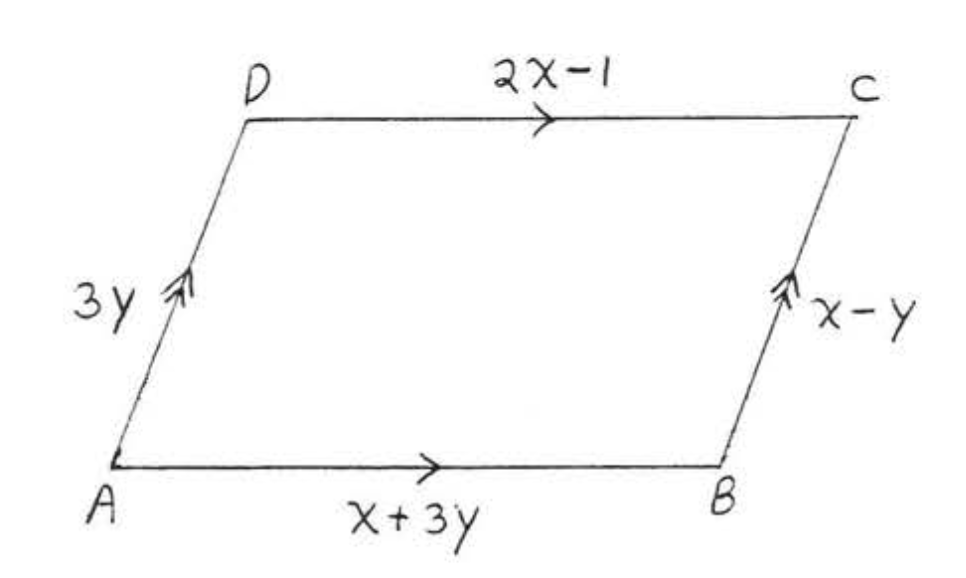
14. Buscar\(x, y, AB, BC, CD\), y\(AD\):
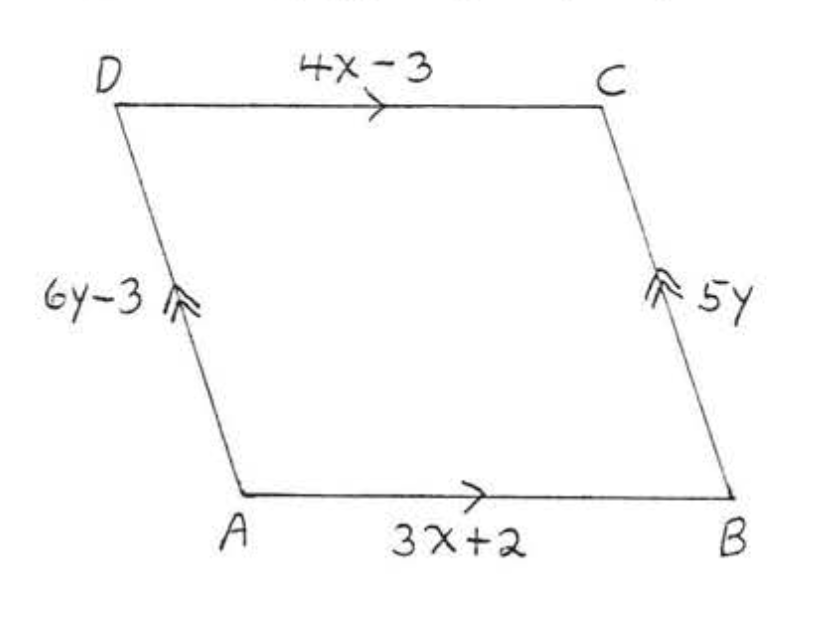
15. Buscar\(x, y, AC\), y\(BD\):
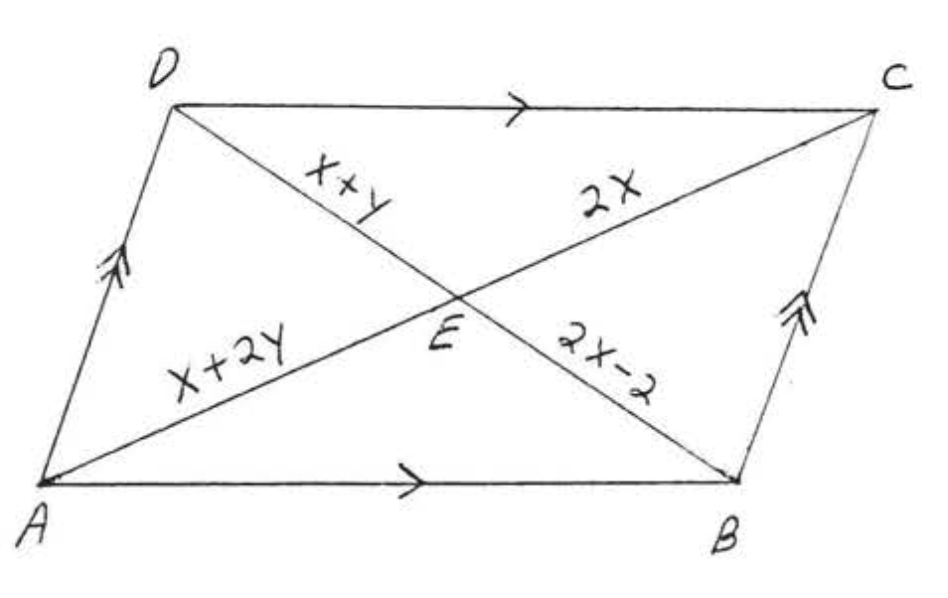
16. Buscar\(x, y, AC\), y\(BD\):
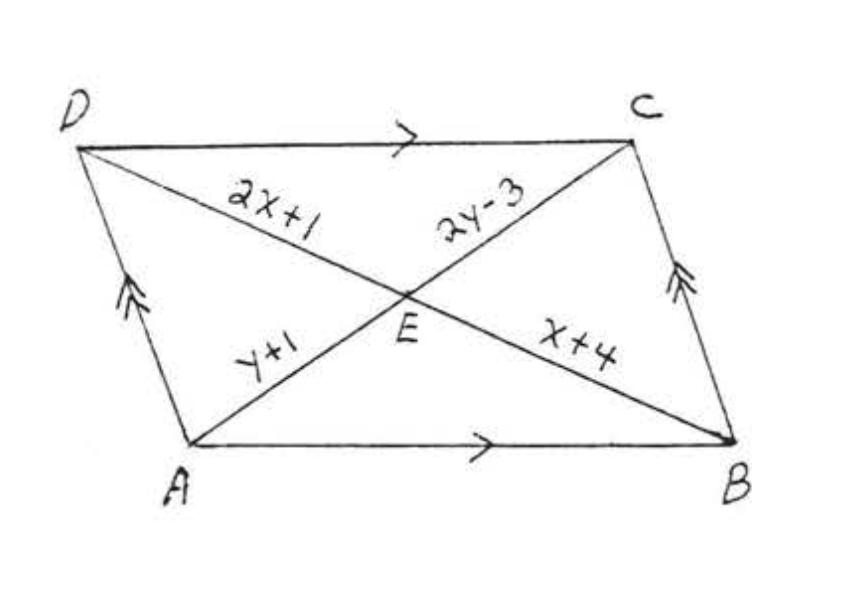
17. Buscar\(x, y, \angle A, \angle B, \angle C\), y\(\angle D\):
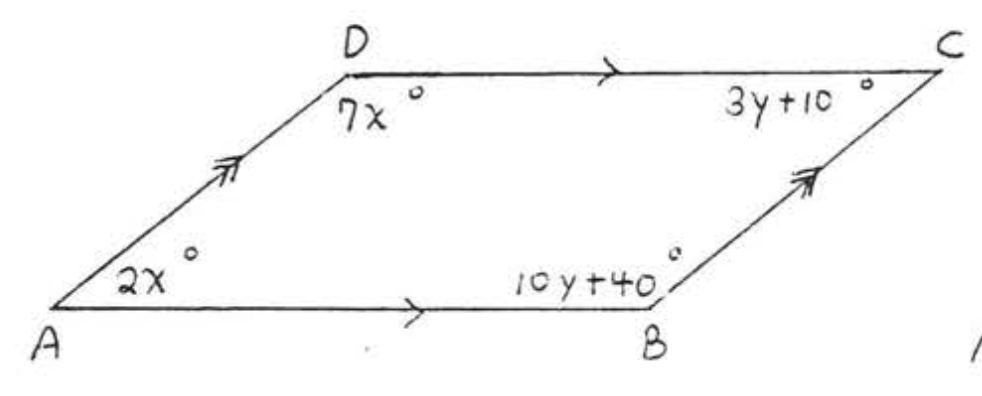
18. Buscar\(x, y, \angle A, \angle B, \angle C\), y\(\angle D\):
