7.5: Circunferencia de un Círculo
- Page ID
- 114747
La circunferencia de un círculo es el perímetro del círculo, la longitud de la línea obtenida cortando el círculo y “enderezando las curvas” (Figura\(\PageIndex{1}\)).
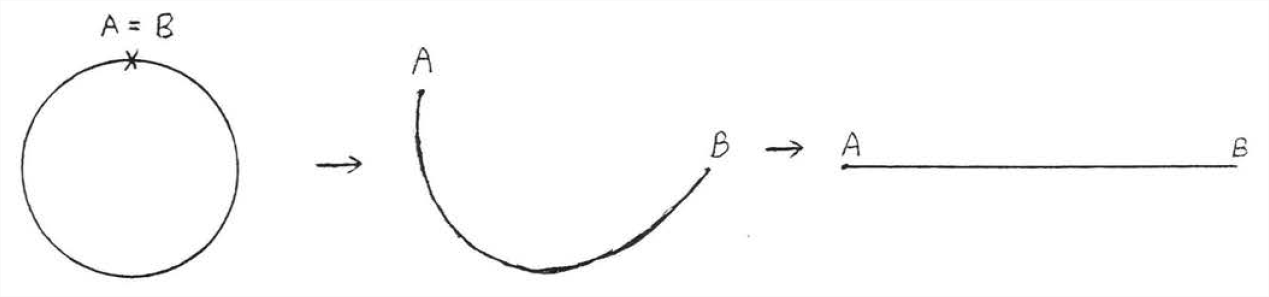
No es práctico medir la circunferencia de la mayoría de los objetos circulares directamente. Una cinta métrica circular sería difícil de sostener en su lugar y se distorsionaría a medida que se doblaría. El objeto en sí sería destruido si intentáramos cortarlo y enderezarlo para su medición. Afortunadamente podemos calcular la circunferencia de un círculo a partir de su radio o diámetro, que son fáciles de medir.
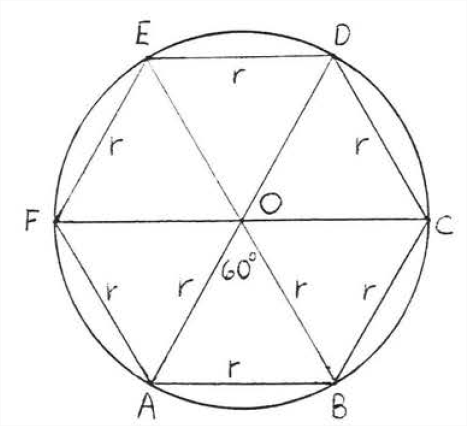
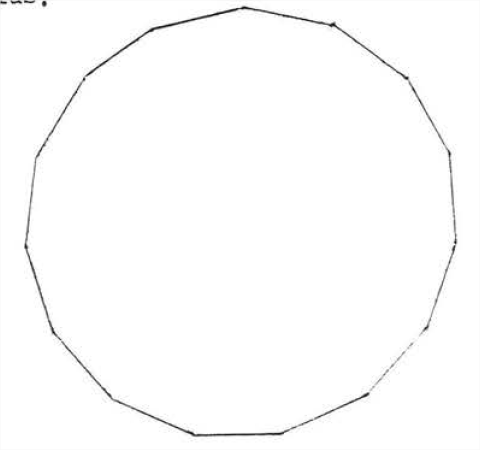
Se\(x\) puede obtener un valor aproximado para la circunferencia de un círculo de radio calculando el perímetro de un hexágono regular de radio\(r\) inscrito en el círculo (Figura\(\PageIndex{2}\)). Vemos que la circunferencia es un poco más que el perímetro del hexágono, que es 6 veces el radio buey 3 veces el diámetro. Para obtener una mejor aproximación, aumentamos el número de lados del polígono regular inscrito. A medida que aumenta el número de lados de un polígono regular, el polígono se parece cada vez más a un círculo (Figura\(\PageIndex{3}\)). En la Sección 7.1, calculamos que el perímetro de un polígono regular de 90 lados era 3.141 veces el diámetro o 6.282 veces el radio. El perímetro de un polígono regular de 1000 lados resultó ser solo un poco más grande, 3.1416 veces el diámetro o 6.283 veces el radio. Por lo tanto, parece razonable concluir que la circunferencia de un círculo es aproximadamente 3.14 veces su diámetro o 6.28 veces su radio.
La circunferencia de un círculo es\(\pi\) por su diámetro o\(2 \pi\) por su radio, donde\(\pi\) es aproximadamente 3.14.
\[C=\pi d\]
o
\[C =2 \pi r\]
El símbolo\(\pi\) (letra griega pi) es notación estándar para el número por el cual se debe multiplicar el diámetro de un círculo para obtener la circunferencia. Su valor suele tomarse como 3.14, aunque 3.1416 y\(\dfrac{22}{7}\) son otras aproximaciones de uso común. Estos números no son exactos, pues como\(\sqrt{2}\), se puede demostrar que\(\pi\) es un número irracional (decimal infinito no repetitivo). Su valor a 50 decimales es
3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37511
Encuentra la circunferencia:
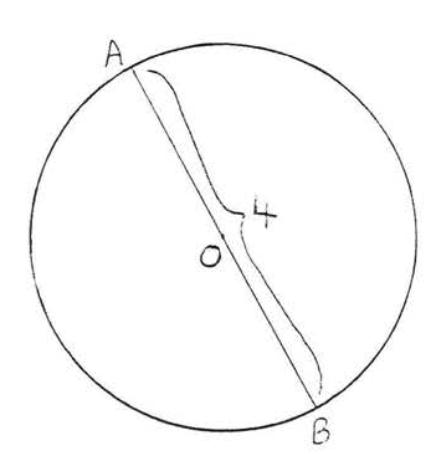
Solución
\(C = \pi d = (3.14)(4) = 12.56\).
Respuesta: 12.56
Definimos la longitud de un arco de la misma manera que definimos la circunferencia. Lo calculamos multiplicando la circunferencia por la fracción apropiada.
Encuentra la longitud del arco\(\widehat{AB}\):
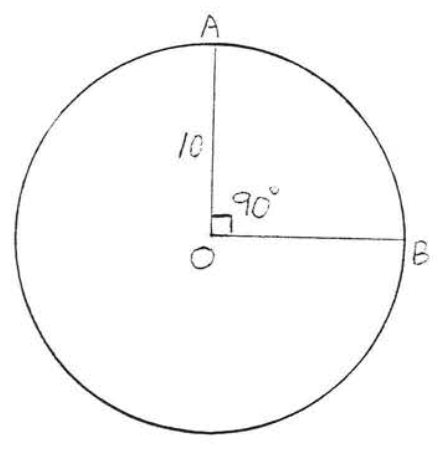
Solución
\(C = 2\pi r = 3(3.14)(10) = 62.8\). Ya que\(90^{\circ}\) es\(\dfrac{1}{4}\) de\(360^{\circ}\),\(\widehat{AB}\) es\(\dfrac{1}{4}\) de la circunferencia\(C\). \(\widehat{AB} = \dfrac{1}{4} C = \dfrac{1}{4} (62.8) = 15.7\).
Respuesta: 15.7.
Como señalamos en la sección 7.4, el símbolo llano = se utilizará para la longitud del arco y el\(\stackrel{\circ}{=}\) símbolo se utilizará para grados. Así en Ejemplo\(PageIndex{2}\),\(\widehat{AB} = 15.7\) pero\(\widehat{AB} \stackrel{\circ}{=} 90^{\circ}\).
También podemos usar la siguiente fórmula para encontrar la longitud del arco:
\[\text{Arc Length} = \dfrac{\text{Degrees in Arc}}{360^{\circ}} \cdot \text{Circumference}\]
o simplemente
\[L = \dfrac{D}{360} \cdot C\]
Así, en el Ejemplo\(\PageIndex{2}\),
\(L = \dfrac{D}{360} \cdot C = \dfrac{90}{360} (62.8) = \dfrac{1}{4} (62.8) = 15.7\)
Encuentra la longitud del arco\(\widehat{AB}\):
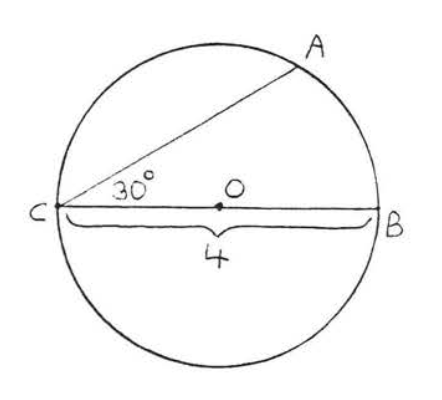
Solución
\(C = \pi d =(3.14)(4) = 12.56\). \(\angle ACB \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB} \stackrel{\circ}{=} 30^{\circ}\). Por lo tanto\(\widehat{AB} \stackrel{\circ}{=} 60^{\circ}\). Usando la fórmula para la longitud del arco,
\(L = \dfrac{D}{360} C = \dfrac{60}{360} (12.56) = \dfrac{1}{6} (12.56) = 2.09\).
Respuesta: 2.09.
Encuentra el diámetro de un círculo cuya circunferencia es 628.
Solución
Dejando\(C = 628\) y\(\pi = 3.14\) en la fórmula para la circunferencia, tenemos
\[\begin{array} {rcl} {c} & = & {\pi d} \\ {628} & = & {(3.14) d} \\ {\dfrac{628}{3.14}} & = & {\dfrac{3.14d}{3.14}} \\ {200} & = & {d} \end{array}\]
Respuesta: diámetro = 200.
El odómetro y velocímetro de un automóvil están calibrados de acuerdo con el número de rotaciones de una de las ruedas. Supongamos que el diámetro de una llanta montada en la rueda es de 2 pies. Entonces su circunferencia son\(C = \pi d = (3.14)(2) = 6.28\) pies. Desde 1 milla = 5280 pies, la rueda girará\(5280 \div 6.28 = 841\) veces cada milla. Si el tamaño de las llantas se cambia por cualquier motivo, el odómetro y el velocímetro deben ser recalibrados.
La circunferencia de la tierra fue calculada primero con precisión por el geógrafo griego Eratóstenes (c. 284 - 192 a.C.), quien vivió en Alejandría, Egipto. Se sabía que al mediodía del día del solsticio de verano los rayos del sol iluminaban por completo los pozos de Siene (ahora llamado Asuán), Egipto. Esto indicó que los rayos del sol eran perpendiculares a la superficie de la Tierra en Syene, y así, en Figura\(\PageIndex{4}\),\(\overleftrightarrow{DS}\) pasa por el centro de la tierra\(O\). Al mismo tiempo, en Alejandría, Eratóstenes observó que los rayos del sol estaban haciendo un ángulo\(\dfrac{1}{50}\) de\(360^{\circ}\) (es decir,\(7.2^{\circ}\)) con la perpendicular (\(\angle BAC = 7.2^{\circ}\)en la Figura\(\PageIndex{4}\)). Se supone que los rayos del sol son paralelos por lo tanto\(\angle AOS = \angle BAC = 7.2^{\circ}\) y\(\widehat{AS} \stackrel{\circ}{=} 7.2^{\circ}\). Dado que la distancia entre Alejandría y Syene es de aproximadamente 500 millas (la longitud de\(\widehat{AS}\)). Eratóstenes pudo llegar a una cifra notablemente precisa de aproximadamente (50) (500) = 25,000 millas para la circunferencia de la tierra.
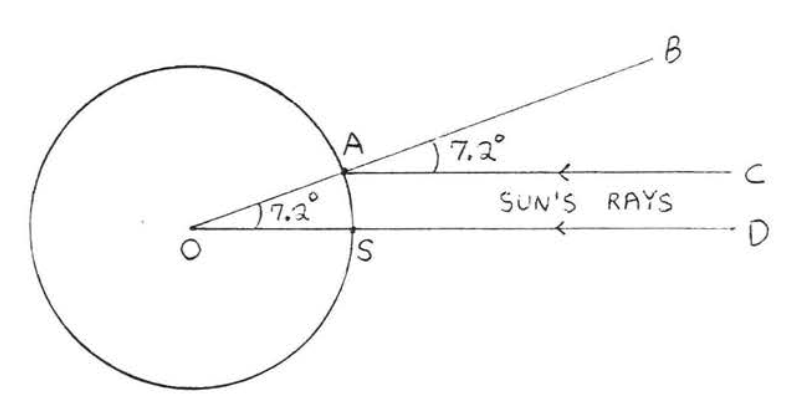
Figura\(\PageIndex{4}\). Los rayos del sol eran perpendiculares a la superficie de la Tierra\(S\) al mismo tiempo que estaban haciendo un ángulo de\(7.2^{\circ}\) con la perpendicular at\(A\).
Las primeras estimaciones brutas del valor de\(\pi\) fueron hechas por los chinos (\(\pi = 3\)), Babilonios (\(\pi = 3\)o\(3\dfrac{1}{8}\)), y egipcios (\(\pi = 3.16\)). El valor\(\pi = 3\) es también el asumido en la Biblia (I Reyes 7:23). El primer cálculo exacto fue realizado por Arquímedes (287 - 212 a.C.), el mayor matemático de la antigüedad, (Arquímedes también fue un famoso físico e inventor. Por ejemplo, descubrió el principio de que un sólido sumergido en un líquido es impulsado por una fuerza igual al peso del fluido desplazado). En su tratado Sobre la medición del círculo se aproxima a la circunferencia calculando los perímetros de polígonos regulares inscritos y circunscritos (Figura\(\PageIndex{5}\)). Esto es similar al método que describimos en el texto excepto que Arquímedes no contaba con tablas trigonométricas precisas y tuvo que derivar sus propias fórmulas, Al llevar el proceso hasta el caso del polígono de 96 lados encontró que el valor de estar entre\(3\dfrac{10}{71}\) y\(3 \dfrac{1}{7}\). (Por cierto, Arquímedes no utilizó realmente el símbolo\(\pi\). El símbolo\(\pi\) no se utilizó para la relación entre la circunferencia y el diámetro de un círculo hasta el siglo XVIII.)
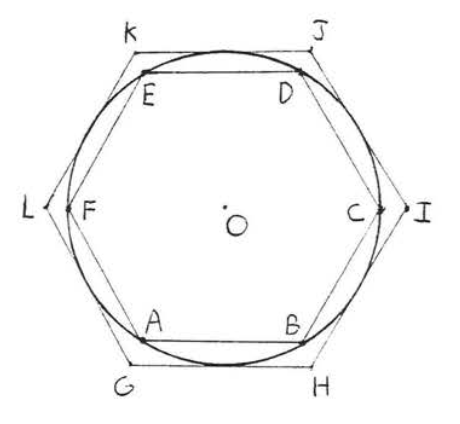
El procedimiento de Arquímedes fue el inicio de una larga historia; de cálculos cada vez más precisos del valor de\(\pi\). Desde el siglo XVII estos cálculos han implicado el uso de series infinitas, como
\[\dfrac{1}{4}\pi = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{9} - ...\]
cuya derivación CA.tl se encuentra en muchos libros de texto de cálculo. Más recientemente, con la ayuda de una computadora, el valor de se\(\pi\) ha determinado a un millón de decimales.
PROBLEMAS
Para cada uno de los siguientes usos\(\pi = 3.14\).
1 - 8. Encuentra la circunferencia de cada círculo:
1.
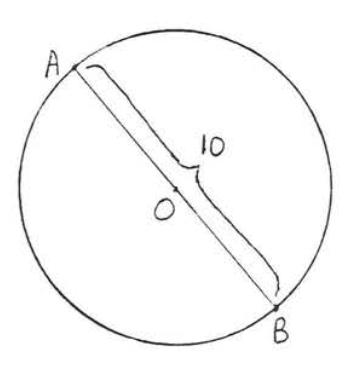
2.
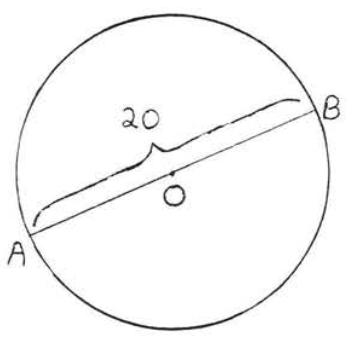
3.
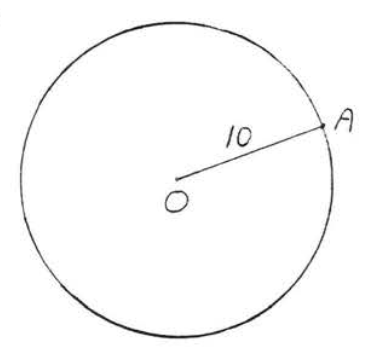
4.
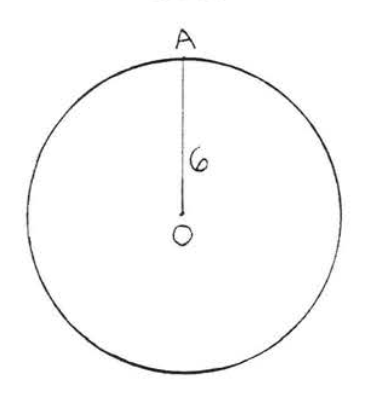
5.
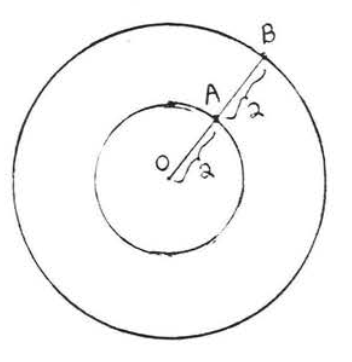
6.
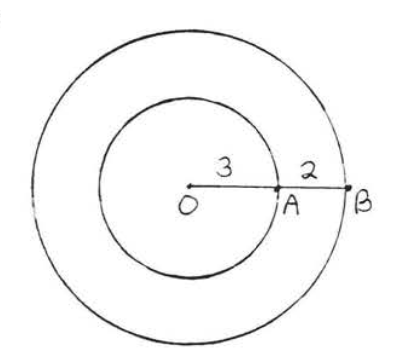
7.
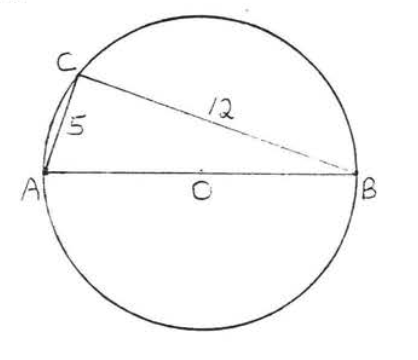
8.
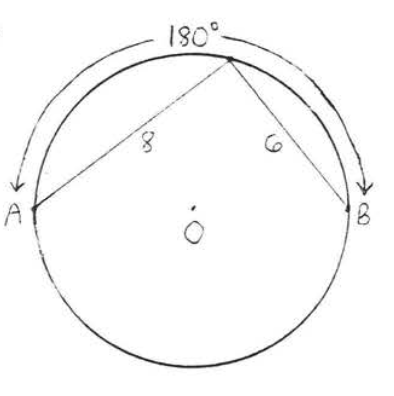
9 - 14. Encuentra la longitud del arco\(\widehat{AB}\):
9.
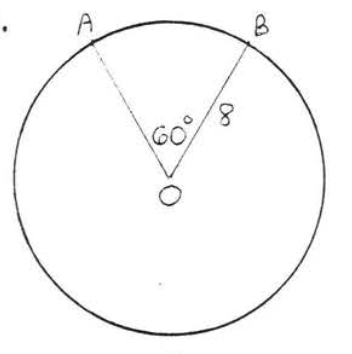
10.
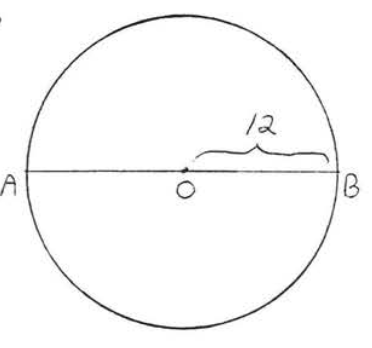
11.
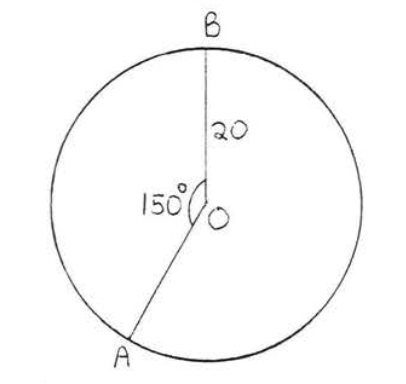
12.
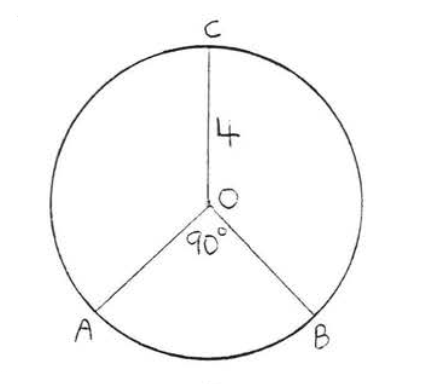
13.
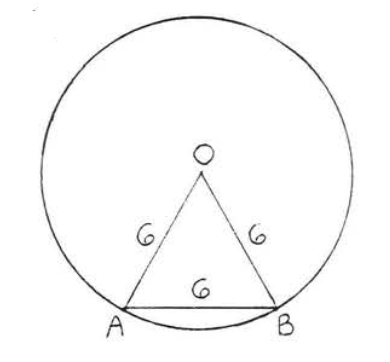
14.
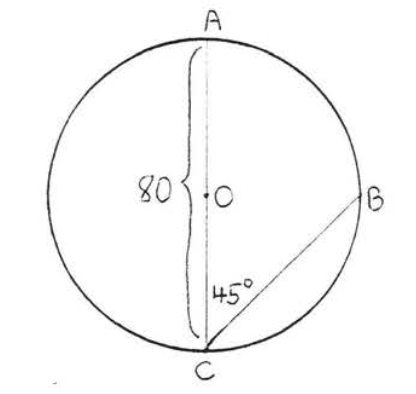
15 - 16. Encuentra las longitudes de los arcos\(\widehat{AB}\) y\(\widehat{CD}\):
15.
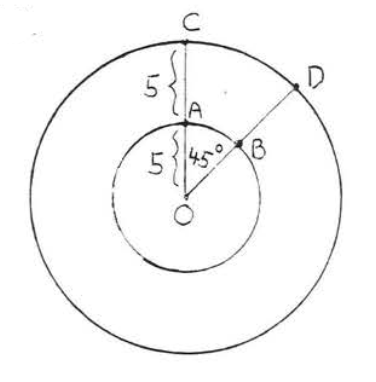
16.
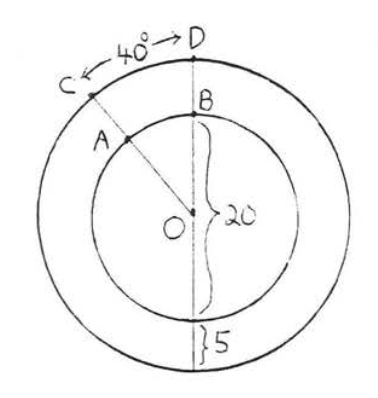
17 - 18. Encuentra la longitud del arco mayor\(\widehat{ABC}\):
17.
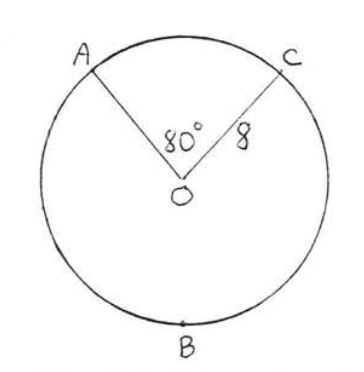
18.
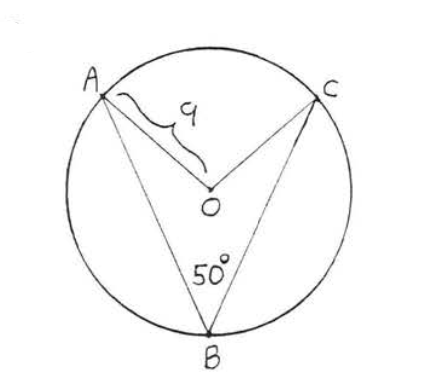
19 - 22. Encuentra la circunferencia del círculo cuyo...
19. diámetro es 30.
20. diámetro es 8.
21. el radio es 10.
22. el radio es 6.
23. Encuentra el radio y diámetro del círculo cuya circunferencia es 314.
24. Encuentra el radio y diámetro del círculo cuya circunferencia es 100 (deja respuesta al número entero más cercano).
25. ¿Cuál es la circunferencia de una rueda de automóvil cuyo diámetro es de 14 pulgadas?
26. ¿Cuál es la circunferencia de un disco fonógrafo de 12 pulgadas?
27. ¿Cuál es el diámetro de la tierra si su circunferencia es de 24,830 millas?
28. ¿Cuál es el diámetro de una pista circular para correr de un cuarto de milla?


