2.5: La regla de la cadena

Última actualización

30 oct 2022
Guardar como PDF
- 2: Derivados
- 2.E: Aplicaciones de Derivados (Ejercicios)

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Hemos cubierto casi todas las reglas derivadas que tratan con combinaciones de dos (o más) funciones. Las operaciones de suma, resta, multiplicación (incluso por una constante) y división llevaron a las reglas de Suma y Diferencia, a la Regla Múltiple Constante, a la Regla de Poder, a la Regla de Producto y a la Regla de Cociente. Para completar la lista de reglas de diferenciación, observamos la última forma en que se pueden combinar dos (o más) funciones: el proceso de composición (es decir, una función “dentro” de otra).

Un ejemplo de una composición de funciones es $f(x) = \cos(x^2)$ . Actualmente no sabemos cómo computar este derivado. Si se ve obligado a adivinar, uno probablemente adivinaría $f^\prime(x) = -\sin(2x)$ , donde reconocemos $-\sin x$ como el derivado de $\cos x$ y $2x$ como el derivado de $x^2$ . Sin embargo, este no es el caso; $f^\prime(x)\neq -\sin(2x)$ . En el Ejemplo 62 veremos la respuesta correcta, que emplea la nueva regla que esta sección introduce, la Regla de Cadena.

Antes de definir esta nueva regla, recordemos la notación para la composición de funciones. Escribimos $(f \circ g)(x)$ o $f(g(x))$ , leemos como " $f$ $g$ de” $x$ , para denotar componer $f$ con $g$ . En taquigrafía, simplemente escribimos $f \circ g$ o $f(g)$ y lo leemos como " $f$ de” $g$ . Antes de dar la regla de diferenciación correspondiente, observamos que la regla se extiende a múltiples composiciones como $f(g(h(x)))$ o $f(g(h(j(x))))$ , etc.

Para motivar la regla, veamos tres derivadas que ya podemos calcular.

Ejemplo 59: Exploración de derivados similares

Encuentra los derivados de

$F_1(x) = (1-x)^2$ ,
$F_2(x) = (1-x)^3,$ y
$F_3(x) = (1-x)^4.$

Veremos más adelante por qué estamos usando subíndices para diferentes funciones y una mayúscula $F$ .

Solución

Para poder utilizar las reglas que ya tenemos, primero debemos expandir cada función como

$F_1(x) = 1 - 2x + x^2$ ,
$F_2(x) = 1 - 3x + 3x^2 - x^3$ y
$F_3(x) = 1 - 4x + 6x^2 - 4x^3 + x^4$ .

No es difícil ver que:

$\begin{align*} F_1^\prime(x) &= -2 + 2x \\[4pt] F_2^\prime(x) &= -3 + 6x - 3x^2 \\[4pt] F_3^\prime (x) &= -4 + 12x - 12x^2 + 4x^3. \end{align*}$

Un dato interesante es que estos pueden reescribirse como

$F_1^\prime (x) = -2(1-x),\quad F_2^\prime(x) = -3(1-x)^2 \text{ and }F_3^\prime (x) = -4(1-x)^3.$

Un patrón podría saltar hacia ti. Reconocer que cada una de estas funciones es una composición, dejando $g(x) = 1-x$ :

$\begin{eqnarray*}F_1(x) = f_1(g(x)),& \text{ where } f_1(x) = x^2,\\ F_2(x) = f_2(g(x)),& \text{ where } f_2(x) = x^3,\\ F_3(x) = f_3(g(x)),& \text{ where } f_3(x) = x^4. \end{eqnarray*}$

Volveremos a este ejemplo después de dar las declaraciones formales de la Regla en Cadena; por ahora, sólo estamos ilustrando un patrón.

Teorema 18: La regla de la cadena

Dejar $y = f(u)$ ser una función diferenciable de $u$ y dejar $u = g(x)$ ser una función diferenciable de $x$ . Entonces $y=f(g(x))$ es una función diferenciable de $x$ , y

$y^\prime = f^\prime(g(x))\cdot g^\prime(x).$

Para ayudar a entender la Regla de la Cadena, volvemos al Ejemplo 59.

Ejemplo 60: Uso de la regla de cadena

Utilice la Regla de Cadena para encontrar las derivadas de las siguientes funciones, como se da en el Ejemplo 59.

Solución

El ejemplo 59 terminó con el reconocimiento de que cada una de las funciones dadas era en realidad una composición de funciones. Para evitar confusiones, ignoramos la mayoría de los subíndices aquí.

$F_1(x) = (1-x)^2$ :

Encontramos que

$y=(1-x)^2 = f(g(x)), \text{ where } f(x) = x^2\ \text{ and }\ g(x) = 1-x.$

Para encontrar $y^\prime$ , aplicamos la Regla de la Cadena. Necesitamos $f^\prime(x)=2x$ y $g^\prime(x)=-1.$

Parte de los usos de la Regla de Cadena $f^\prime(g(x))$ . Esto significa $g(x)$ sustituto $x$ en la ecuación para $f^\prime(x)$ . Es decir, $f^\prime(x) = 2(1-x)$ . Terminando la regla de la cadena que tenemos

$y^\prime = f^\prime(g(x))\cdot g^\prime(x) = 2(1-x)\cdot (-1) = -2(1-x)= 2x-2.$

$F_2(x) = (1-x)^3$ :

Vamos $y = (1-x)^3 = f(g(x))$ , dónde $f(x) = x^3$ y $g(x) = (1-x)$ . Tenemos $f^\prime(x) = 3x^2$ , entonces $f^\prime(g(x)) = 3(1-x)^2$ . La regla de la cadena entonces establece

$y^\prime = f^\prime(g(x))\cdot g^\prime (x) = 3(1-x)^2\cdot(-1) = -3(1-x)^2.$

$F_3(x) = (1-x)^4$ :

Por último $y = (1-x)^4$ , cuando, tenemos $f(x)= x^4$ y $g(x) = (1-x)$ . Así $f^\prime(x) = 4x^3$ y $f^\prime(g(x)) = 4(1-x)^3$ . Así

$y^\prime = f^\prime(g(x))\cdot g^\prime(x) = 4(1-x)^3\cdot (-1) = -4(1-x)^3.$

El ejemplo 60 demostró un patrón particular: cuándo $f(x)=x^n$ , entonces $y^\prime =n\cdot (g(x))^{n-1}\cdot g^\prime (x)$ . A esto se le llama la Regla Generalizada del Poder.

Teorema 19: Regla de Poder Generalizada

Dejar $g(x)$ ser una función diferenciable y dejar $n\neq 0$ ser un entero. Entonces

$\dfrac{d}{dx}\Big(g(x)^n\Big) = n\cdot \big(g(x)\big)^{n-1}\cdot g^\prime (x).$

Esto nos permite encontrar rápidamente la derivada de funciones como $y = (3x^2-5x+7+\sin x)^{20}$ . Si bien puede parecer intimidante, la Regla Generalizada del Poder establece que

$y^\prime = 20(3x^2-5x+7+\sin x)^{19}\cdot (6x-5+\cos x).$

Tratar el proceso de toma de derivados paso a paso. En el ejemplo que se acaba de dar, primero multiplicar por 20, luego reescribir el interior de los paréntesis, elevándolo todo a la $^{\text{th}}$ potencia 19. Entonces piensa en la derivada de la expresión dentro de los paréntesis, y multiplícalo por eso.

Consideramos ahora más ejemplos que emplean la Regla de la Cadena.

Ejemplo 61: Uso de la regla de la cadena

Encuentra las derivadas de las siguientes funciones:

$y = \sin{2x}$
$y= \ln (4x^3-2x^2)$
$y = e^{-x^2}$

Solución

Considerar $y = \sin 2x$ . Reconocer que esta es una composición de funciones, dónde $f(x) = \sin x$ y $g(x) = 2x$ . Así $y^\prime = f^\prime(g(x))\cdot g^\prime(x) = \cos (2x)\cdot 2 = 2\cos 2x.$
Reconocer que $y = \ln (4x^3-2x^2)$ es la composición de $f(x) = \ln x$ y $g(x) = 4x^3-2x^2$ . Además, recordemos que $\dfrac{d}{dx}\Big(\ln x\Big) = \dfrac{1}{x}.$ Esto nos lleva a: $y^\prime = \dfrac{1}{4x^3-2x^2} \cdot (12x^2-4x) = \dfrac{12x^2-4x}{4x^3-2x^2}= \dfrac{4x(3x-1)}{2x(2x^2-x)} = \dfrac{2(3x-1)}{2x^2-x}.$
Reconocer que $y = e^{-x^2}$ es la composición de $f(x) = e^x$ y $g(x) = -x^2$ . Recordando eso $f^\prime(x) = e^x$ , tenemos $y^\prime = e^{-x^2}\cdot (-2x) = (-2x)e^{-x^2}.$

Ejemplo 62: Uso de la regla de cadena para encontrar una línea tangente

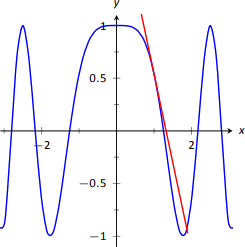
Vamos $f(x) = \cos x^2$ . Encuentra la ecuación de la línea tangente a la gráfica de $f$ at $x=1$ .

Solución

La línea tangente pasa por el punto $(1,f(1)) \approx (1,0.54)$ con pendiente $f^\prime(1)$ . Para encontrar $f^\prime$ , necesitamos la Regla de la Cadena.

$f^\prime(x) = -\sin(x^2) \cdot(2x) = -2x\sin x^2$ . Evaluado en $x=1$ , tenemos $f^\prime(1) = -2\sin 1\approx -1.68$ . Así, la ecuación de la línea tangente es

$y = -1.68(x-1)+0.54 .$

La línea tangente se esboza junto con $f$ la Figura 2.17.

Figura 2.17: $f(x)=\cos x^2$ esbozado junto con su línea tangente en $x=1$ .

La regla de la cadena se usa a menudo para tomar derivados. Debido a esto, uno puede familiarizarse con el proceso básico y aprender patrones que faciliten encontrar derivados rápidamente. Por ejemplo,

$\dfrac{d}{dx}\Big(\ln (\text{anything})\Big) = \dfrac{1}{\text{anything}}\cdot (\text{anything})^\prime = \dfrac{(\text{anything})^\prime}{\text{anything}}.$

Un ejemplo concreto de esto es

$\dfrac{d}{dx}\Big(\ln(3x^{15}-\cos x+e^x)\Big) = \dfrac{45x^{14}+\sin x+e^x}{3x^{15}-\cos x+e^x}.$ Si bien el derivado puede parecer intimidante al principio, busque el patrón. El denominador es el mismo que lo que estaba dentro de la función logarítmica natural; el numerador es simplemente su derivada.

Este proceso de reconocimiento de patrones se puede aplicar a muchas funciones. En general, en lugar de escribir “cualquier cosa”, utilizamos $u$ como función genérica de $x$ . Entonces decimos

$\dfrac{d}{dx}\Big(\ln u\Big) = \dfrac{u^\prime}{u}.$

La siguiente es una breve lista de cómo la Regla de Cadena se puede aplicar rápidamente a funciones familiares.

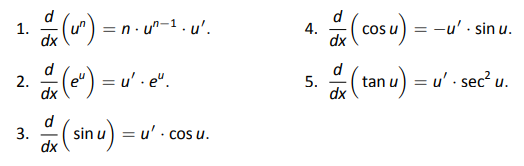
$clipboard_eccb9450ef7e1a3d7b13849b9fdff4cc7.png$

Por supuesto, la Regla de la Cadena se puede aplicar en conjunto con cualquiera de las otras reglas que ya hemos aprendido. Practicamos esto a continuación.

Ejemplo 63: Uso de las reglas de producto, cociente y cadena

Encuentra las derivadas de las siguientes funciones.

$f(x) = x^5 \sin{2x^3}$
$f(x) = \dfrac{5x^3}{e^{-x^2}}$ .

Solución

Debemos usar las Reglas de Productos y Cadenas. No piense que debe ser capaz de “ver” la respuesta completa de inmediato; más bien, simplemente proceda paso a paso. $f^\prime(x) = x^5\big(6x^2\cos 2x^3\big) + 5x^4\big(\sin 2x^3\big)= 6x^7\cos2x^3+5x^4\sin 2x^3.$
Debemos emplear la Regla del Cociente junto con la Regla de las Cadenas. Nuevamente, proceda paso a paso. $\begin{align*} f^\prime(x) = \dfrac{e^{-x^2}\big(15x^2\big) - 5x^3\big((-2x)e^{-x^2}\big)}{\big(e^{-x^2}\big)^2} &=\dfrac{e^{-x^2}\big(10x^4+15x^2\big)}{e^{-2x^2}}\\ &= e^{x^2}\big(10x^4+15x^2\big). \end{align*}$

Una clave para trabajar correctamente estos problemas es descomponer el problema en piezas más pequeñas y manejables. Por ejemplo, al usar las Reglas de Producto y Cadena juntas, solo considere la primera parte de la Regla del Producto al principio: $f(x)g^\prime(x)$ . Solo reescribe $f(x)$ , luego encuentra $g^\prime(x)$ . Después pasar a la $f^\prime(x)g(x)$ parte. No intentes averiguar ambas partes a la vez.

De igual manera, utilizando la Regla del Cociente, acércate al numerador en dos pasos y maneja el denominador después de completarlo. Solo simplifique después.

También podemos emplear la propia Regla de Cadena varias veces, como se muestra en el siguiente ejemplo.

Ejemplo 64: Uso de la regla de cadena varias veces

Encuentra la derivada de $y = \tan^5(6x^3-7x)$ .

Solución

Reconocer que tenemos la $g(x)=\tan(6x^3-7x)$ función “dentro” de la $f(x)=x^5$ función; es decir, tenemos $y = \big(\tan(6x^3-7x)\big)^5$ . Comenzamos a usar la Regla de Poder Generalizado; en este primer paso, no computamos completamente la derivada. Más bien, nos estamos acercando a este paso a paso.

$y^\prime = 5\big(\tan(6x^3-7x)\big)^4\cdot g^\prime(x).$

Ahora encontramos $g^\prime(x)$ . Nuevamente necesitamos la Regla de la Cadena;

$g^\prime(x) = \sec^2(6x^3-7x)\cdot(18x^2-7).$ Combine esto con lo que encontramos anteriormente para dar

$\begin{align*} y^\prime &= 5\big(\tan(6x^3-7x)\big)^4\cdot\sec^2(6x^3-7x)\cdot(18x^2-7)\\ &= (90x^2-35)\sec^2(6x^3-7x)\tan^4(6x^3-7x). \end{align*}$

Esta función es francamente una función ridícula, que no posee ningún valor práctico real. Es muy difícil graficar, ya que la función tangente tiene muchas asíntotas verticales y $6x^3-7x$ crece muy rápido. Lo importante que hay que aprender de esto es que se puede encontrar el derivado. De hecho, no es “difícil”; hay que dar varios pasos simples y tener cuidado de hacer un seguimiento de cómo aplicar cada uno de estos pasos.

Es un ejercicio matemático tradicional encontrar las derivadas de funciones arbitrariamente complicadas solo para demostrar que se puede hacer. Simplemente divida todo en trozos más pequeños.

Ejemplo 65: Uso de las reglas de producto, cociente y cadena

Encuentra la derivada de $f(x) = \dfrac{x\cos(x^{-2})-\sin^2(e^{4x})}{\ln(x^2+5x^4)}.$

Solución

Es probable que esta función no tenga ningún uso práctico fuera de demostrar habilidades derivadas. A continuación se da la respuesta sin simplificación. Emplea tres veces la Regla del Cociente, la Regla del Producto y la Regla de Cadena.

$f^\prime(x) = \dfrac{\Big(\ln(x^2+5x^4)\Big)\cdot\Big[\big(x\cdot(-\sin(x^{-2}))\cdot(-2x^{-3})+1\cdot \cos(x^{-2})\big)-2\sin(e^{4x})\cdot\cos(e^{4x})\cdot(4e^{4x})\Big]-\Big(x\cos(x^{-2})-\sin^2(e^{4x})\Big)\cdot\dfrac{2x+20x^3}{x^2+5x^4}}{\big(\ln(x^2+5x^4)\big)^2}.$

El lector está muy animado a mirar cada término y reconocer por qué está ahí. (Es decir, se utiliza la Regla del Cociente; en el numerador, identificar el término “LODHi”, etc.) Este ejemplo demuestra que los derivados se pueden computar sistemáticamente, sin importar cuán arbitrariamente complicada sea la función.

La regla de la cadena también tiene valor teórico. Es decir, se puede utilizar para encontrar las derivadas de funciones que aún no hemos aprendido como lo hacemos en el siguiente ejemplo.

Ejemplo 66: La regla de la cadena y funciones exponenciales

Usa la Regla de Cadena para encontrar la derivada de $y= a^x$ donde $a>0$ , $a\neq 1$ es constante.

Solución

Sólo sabemos encontrar la derivada de una función exponencial: $y = e^x$ ; este problema nos está pidiendo encontrar la derivada de funciones como $y = 2^x$ .

Esto se puede lograr reescribiendo $a^x$ en términos de $e$ . Recordando que $e^x$ y $\ln x$ son funciones inversas, podemos escribir

$a = e^{\ln a} \quad \text{and so } \quad y = a^x = e^{\ln (a^x)}. \nonumber$

Por la propiedad exponente de logaritmos, podemos “derribar” el poder para obtener

$y = a^x = e^{x (\ln a)}. \nonumber$

La función es ahora la composición $y=f(g(x))$ , con $f(x) = e^x$ y $g(x) = x(\ln a)$ . Desde $f^\prime(x) = e^x$ y $g^\prime(x) = \ln a$ , la Regla de la Cadena da

$y^\prime = e^{x (\ln a)} \cdot \ln a. \nonumber$

Recordemos que el $e^{x(\ln a)}$ término en el lado derecho es justo $a^x$ , nuestra función original. Así, la derivada contiene la propia función original. Tenemos

$y^\prime = y \cdot \ln a = a^x\cdot \ln a. \nonumber$

La Regla de Cadena, aunada a la regla derivada de $e^x$ , nos permite encontrar las derivadas de todas las funciones exponenciales.

El ejemplo anterior produjo un resultado digno de su propia “caja”.

Teorema 20: Derivadas de las Funciones Exponenciales

Vamos $f(x)=a^x$ , para $a>0, a\neq 1$ . Entonces $f$ es diferenciable para todos los números reales y

$f^\prime(x) = \ln a\cdot a^x. \nonumber$

Notación de regla de cadena alternativa

Es instructivo entender cómo “se ve” la Regla de Cadena usando la notación " $\dfrac{dy}{dx}$ "” en lugar de la $y^\prime$ notación. Supongamos que $y=f(u)$ es una función de $u$ , donde $u=g(x)$ es una función de $x$ , como se afirma en el Teorema 18. Entonces, a través de la composición $f \circ g$ , podemos pensar en $y$ como una función de $x$ , como $y=f(g(x))$ . Así la derivada de $y$ con respecto a tiene $x$ sentido; podemos hablar de $\dfrac{dy}{dx}.$ Esto nos lleva a una interesante progresión de la notación:

\[\begin{align*}y^\prime &= f^\prime(g(x))\cdot g^\prime(x) \\ \dfrac{dy}{dx} &= y^\prime(u) \cdot u^\prime(x)\quad \text{(since $y=f(u)$ and $u=g(x)$ )}\\ \dfrac{dy}{dx} &= \dfrac{dy}{du} \cdot \dfrac{du}{dx}\quad \text{(using "fractional'' notation for the derivative)}\end{align*}\]

Aquí destaca el aspecto “fraccionario” de la notación derivada. En el lado derecho, parece que los términos " $du$ " cancelan, dejando

$\dfrac{dy}{dx} = \dfrac{dy}{dx}.$

Es importante darse cuenta de que no estamos cancelando estos términos; la notación derivada de $\dfrac{dy}{dx}$ es un símbolo. Es igualmente importante darse cuenta de que esta notación fue elegida precisamente por este comportamiento. Hace que aplicar la Regla de Cadena sea fácil con múltiples variables. Por ejemplo,

$\dfrac{dy}{dt} = \dfrac{dy}{d\bigcirc} \cdot \dfrac{d\bigcirc}{d\triangle} \cdot \dfrac{d\triangle}{dt}.$

donde $\bigcirc$ y $\triangle$ son las variables que te gustaría usar.

Una de las formas más comunes de “visualizar” la Regla de Cadena es considerar un conjunto de engranajes, como se muestra en la Figura 2.18. Los engranajes tienen 36, 18 y 6 dientes, respectivamente. Eso significa que por cada revolución del $x$ engranaje, el $u$ engranaje gira dos veces. Es decir, la velocidad a la que el $u$ engranaje hace una revolución es dos veces más rápida que la velocidad a la que el $x$ engranaje hace una revolución. Utilizando la terminología del cálculo, la tasa $u$ de cambio, con respecto a $x$ , es $\dfrac{du}{dx} = 2$ .

Figura 2.18: Una serie de engranajes para demostrar la Regla de Cadena. Observe cómo $\dfrac{dy}{dx}=\dfrac{dy}{du}\cdot\dfrac{du}{dx}$ .

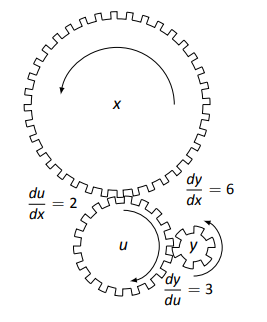
De igual manera, cada revolución de $u$ causa 3 revoluciones de $y$ : $\dfrac{dy}{du} = 3$ . ¿Cómo $y$ cambia con respecto a $x$ ? Para cada revolución de $x$ , $y$ gira 6 veces; es decir,

$\dfrac{dy}{dx} = \dfrac{dy}{du}\cdot \dfrac{du}{dx} = 2\cdot 3 = 6.$

Entonces podemos extender la Regla de Cadena con más variables agregando más engranajes a la imagen.

Es difícil exagerar la importancia de la Regla en Cadena. Muy a menudo las funciones con las que nos ocupamos son composiciones de dos o más funciones, requiriendo que usemos esta regla para computar derivadas. A menudo se usa en la práctica cuando se desconocen las funciones reales. Más bien, a través de la medición, podemos calcular $\dfrac{dy}{du}$ y $\dfrac{du}{dx}$ . Con nuestro conocimiento de la Regla de la Cadena, encontrar $\dfrac{dy}{dx}$ es sencillo.

En la siguiente sección, utilizamos la Regla de Cadena para justificar otra técnica de diferenciación. Hay muchas curvas que podemos dibujar en el plano que fallan en la “prueba de línea vertical”. Por ejemplo, considere $x^2+y^2=1$ , que describe el círculo unitario. Todavía podemos estar interesados en encontrar pendientes de líneas tangentes al círculo en varios puntos. La siguiente sección muestra cómo podemos encontrar $\dfrac{dy}{dx}$ sin primero “resolver para” $y$ . Si bien podemos en esta instancia, en muchas otras instancias resolver por $y$ es imposible. En estas situaciones, la diferenciación implícita es indispensable.

Search

Text Color

Text Size

Margin Size

Font Type

Notación de regla de cadena alternativa

Support Center

How can we help?