14.5: La regla de cadena para funciones multivariables

Objetivos de aprendizaje

• Declarar las reglas de cadena para una o dos variables independientes.
• Utilice diagramas de árbol como ayuda para comprender la regla de la cadena para varias variables independientes e intermedias.
• Realizar diferenciación implícita de una función de dos o más variables.

En el cálculo de una sola variable, encontramos que una de las reglas de diferenciación más útiles es la regla de cadena, que nos permite encontrar la derivada de la composición de dos funciones. Lo mismo es cierto para el cálculo multivariable, pero esta vez tenemos que lidiar con más de una forma de la regla de la cadena. En esta sección, estudiamos extensiones de la regla de la cadena y aprendemos a tomar derivadas de composiciones de funciones de más de una variable.

Reglas de cadena para una o dos variables independientes

Recordemos que la regla de la cadena para la derivada de un compuesto de dos funciones puede escribirse en la forma

$$\dfrac{d}{dx}\Big(f(g(x))\Big)=f′\big(g(x)\big)g′(x). \nonumber$$

En esta ecuación, ambos$f(x)$ y$g(x)$ son funciones de una variable. Ahora supongamos que$f$ es una función de dos variables y$g$ es una función de una variable. O tal vez ambas son funciones de dos variables, o incluso más. ¿Cómo calcularíamos la derivada en estos casos? El siguiente teorema nos da la respuesta para el caso de una variable independiente.

Regla de cadena para una variable independiente

Supongamos que$x=g(t)$ y$y=h(t)$ son funciones diferenciables de$t$ y$z=f(x,y)$ es una función diferenciable de$x$ y$y$. Entonces$z=f(x(t),y(t))$ es una función diferenciable de$t$ y

$$\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}, \label{chain1}$$

donde se evalúan los derivados ordinarios$t$ y los derivados parciales se evalúan en$(x,y)$.

Prueba

La prueba de este teorema utiliza la definición de diferenciabilidad de una función de dos variables. Supongamos que$f$ es diferenciable en el punto$P(x_0,y_0),$ donde$x_0=g(t_0)$ y$y_0=h(t_0)$ para un valor fijo de$t_0$. Deseamos demostrar que$z=f\big(x(t),y(t)\big)$ es diferenciable en$t=t_0$ y que la Ecuación\ ref {cadena1} se mantiene en ese punto también.

Ya que$f$ es diferenciable en$P$, sabemos que

$$z(t)=f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x−x_0)+f_y(x_0,y_0)(y−y_0)+E(x,y), \nonumber$$

donde

$$\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}=0. \nonumber$$

Luego restamos$z_0=f(x_0,y_0)$ de ambos lados de esta ecuación:

$$\begin{align*} z(t)−z(t_0) &=f(x(t),y(t))−f(x(t_0),y(t_0)) \\[4pt] &=f_x(x_0,y_0)(x(t)−x(t_0))+f_y(x_0,y_0)(y(t)−y(t_0))+E(x(t),y(t)). \end{align*}$$

A continuación, dividimos ambos lados por$t−t_0$:

$$\frac{z(t)−z(t_0)}{t−t_0}=f_x(x_0,y_0)\frac{x(t)−x(t_0)}{t−t_0}+f_y(x_0,y_0)\frac{y(t)−y(t_0)}{t−t_0}+\frac{E(x(t),y(t))}{t−t_0}. \nonumber$$

Entonces tomamos el límite como$t$ acercamientos$t_0$:

$$\begin{align*} \lim_{t→t_0}\dfrac{z(t)−z(t_0)}{t−t_0} &= f_x(x_0,y_0)\lim_{t→t_0} \left (\dfrac{x(t)−x(t_0)}{t−t_0} \right) \\[4pt] &+f_y(x_0,y_0)\lim_{t→t_0}\left (\dfrac{y(t)−y(t_0)}{t−t_0}\right)\\[4pt] &+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \end{align*}$$

El lado izquierdo de esta ecuación es igual a$dz/dt$, lo que lleva a

$$\dfrac{dz}{dt}=f_x(x_0,y_0)\dfrac{dx}{dt}+f_y(x_0,y_0)\dfrac{dy}{dt}+\lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0}. \nonumber$$

El último término puede ser reescrito como

$$\begin{align*} \lim_{t→t_0}\dfrac{E(x(t),y(t))}{t−t_0} &=\lim_{t→t_0}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}) \\[4pt] &=\lim_{t→t_0}\left(\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\right)\lim_{t→t_0}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \end{align*} \nonumber$$

A medida$\big(x(t_0),y(t_0)\big),$ que$t_0, \big(x(t),y(t)\big)$ se$t$ aproxima se aproxima para que podamos reescribir el último producto como

$$\lim_{(x,y)→(x_0,y_0)}\dfrac{E(x,y)}{\sqrt{(x−x_0)^2+(y−y_0)^2}}\lim_{(x,y)→(x_0,y_0)}\left(\dfrac{\sqrt{(x−x_0)^2+(y−y_0)^2}}{t−t_0}\right). \nonumber$$

Dado que el primer límite es igual a cero, solo necesitamos mostrar que el segundo límite es finito:

$$\begin{align*} \lim_{(x,y)→(x_0,y_0)} \dfrac{\sqrt{ (x−x_0)^2+(y−y_0)^2 }} {t−t+0} =\lim_{(x,y)→(x_0,y_0)} \sqrt{ \dfrac { (x−x_0)^2+(y−y_0)^2 } {(t−t_0)^2} } \\[4pt] =\lim_{(x,y)→(x_0,y_0)}\sqrt{ \left(\dfrac{x−x_0}{t−t_0}\right)^2+\left(\dfrac{y−y_0}{t−t_0}\right)^2} \\[4pt] =\sqrt{ \left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{x−x_0}{t−t_0}\right)\right]^2+\left[\lim_{(x,y)→(x_0,y_0)} \left(\dfrac{y−y_0}{t−t_0}\right)\right]^2}. \end{align*} \nonumber$$

Dado que$x(t)$ y$y(t)$ son ambas funciones diferenciables de$t$, ambos límites dentro del último radical existen. Por lo tanto, este valor es finito. Esto prueba la regla de la cadena en$t=t_0$; el resto del teorema se desprende de la suposición de que todas las funciones son diferenciables en todos sus dominios.

□

Un examen más detallado de la Ecuación\ ref {cadena1} revela un patrón interesante. El primer término en la ecuación es$\dfrac{∂f}{∂x} \cdot \dfrac{dx}{dt}$ y el segundo término es$\dfrac{∂f}{∂y}⋅\dfrac{dy}{dt}$. Recordemos que al multiplicar fracciones, se puede utilizar la cancelación. Si tratamos estos derivados como fracciones, entonces cada producto “simplifica” a algo parecido$∂f/dt$. Las variables$x$ y$y$ que desaparecen en esta simplificación suelen denominarse variables intermedias: son variables independientes para la función$f$, pero son variables dependientes para la variable$t$. Dos términos aparecen en el lado derecho de la fórmula, y$f$ es una función de dos variables. Este patrón también funciona con funciones de más de dos variables, como vemos más adelante en esta sección.

Ejemplo$\PageIndex{1}$: Using the Chain Rule

Calcular$dz/dt$ para cada una de las siguientes funciones:

1. $z=f(x,y)=4x^2+3y^2,\quad x=x(t)=\sin t,\quad y=y(t)=\cos t$
2. $z=f(x,y)=\sqrt{x^2−y^2},\quad x=x(t)=e^{2t},\quad y=y(t)=e^{−t}$

Solución

a. Para usar la regla de la cadena, necesitamos cuatro cantidades$∂z/∂x,\; ∂z/∂y, \; dx/dt$, y$dy/dt$:

• $\dfrac{∂z}{∂x}=8x$
• $\dfrac{dx}{dt}=\cos t$
• $\dfrac{∂z}{∂y}=6y$
• $\dfrac{dy}{dt}=−\sin t$

Ahora, sustituimos cada uno de estos en la Ecuación\ ref {cadena1}:

\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {\ z parcial} {\ parcial x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ z parcial} {\ parcial y}\ cdot\ dfrac {dy} {dt}\\ [4pt]
& =( 8x) (\ cos t) + (6y) (−\ sin t)\\ [4pt]
&=8x\ cos t−6y\ sin t.\ end {align*}\]

Esta respuesta tiene tres variables en ella. Para reducirlo a una variable, utilice el hecho de que$x(t)=\sin t$ y$y(t)=\cos t.$ Obtenemos

\ [\ begin {align*}\ dfrac {dz} {dt} &=8x\ cos t−6y\ sin t\\ [4pt]
&=8 (\ sin t)\ cos t−6 (\ cos t)\ sin t\\ [4pt]
&=2\ sin t\ cos t.\ end {align*}\]

Esta derivada también se puede calcular sustituyendo primero$x(t)$ y$f(x,y),$ luego$y(t)$ diferenciando con respecto a$t$:

\ [\ begin {align*} z =f (x, y) &=f\ grande (x (t), y (t)\ grande)\\ [4pt]
&=4 (x (t)) ^2+3 (y (t)) ^2\\ [4pt]
&=4\ sen ^2 t+3\ cos^2 t.\ end {align*}\]

Entonces

\ [\ begin {align*}\ dfrac {dz} {dt} &=2 (4\ sin t) (\ cos t) +2 (3\ cos t) (−\ sin t)\\ [4pt]
&=8\ sin t\ cos t−6\ sin t\ cos t\ [4pt]
&=2\ sin t\ cos t,\ end {align*}\]

que es la misma solución. Sin embargo, puede que no siempre sea así de fácil diferenciar en esta forma.

b. Para usar la regla de la cadena, nuevamente necesitamos cuatro cantidades,$∂z/∂x,∂z/dy,dx/dt,$ y$dy/dt:$

• $\dfrac{∂z}{∂x}=\dfrac{x}{\sqrt{x^2−y^2}}$
• $\dfrac{dx}{dt}=2e^{2t}$
• $\dfrac{∂z}{∂y}=\dfrac{−y}{\sqrt{x^2−y^2}}$
• $\dfrac{dx}{dt}=−e^{−t}.$

Sustituimos cada uno de estos en la Ecuación\ ref {cadena1}:

\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {\ parcial z} {\ parcial x}\ cdot\ dfrac {dx} {dt} +\ dfrac {\ parcial z} {\ parcial y}\ cdot\ dfrac {dy} {dt}\\ [4pt] &=\ izquierda (\ dfrac {x} {\ sqrt {x^2−y^2}}\ derecha) (2e^ {2t}) +\ izquierda (\ dfrac {−y} {\ sqrt {x^2−y^2}}\ derecha) (−e^ {−t})\\ [4pt]
&=\ dfrac {2xe^ {2t} −ye^ {−t}} { sqrt {x^2−y^2}}. \ end {align*}\ nonumber\]

Para reducir esto a una variable, utilizamos el hecho de que$x(t)=e^{2t}$ y$y(t)=e^{−t}$. Por lo tanto,

\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {2xe^2t+ye^ {−t}} {\ sqrt {x^2−y^2}}\\ [4pt]
&=\ dfrac {2 (e^ {2t}) e^ {2t} + (e^ {−t}) e^ −^ {t}} {\ sqrt {e^ {4t} −e^ {−2t}}}\\ [4pt]
&=\ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}}}. \ end {align*}\ nonumber\]

Para eliminar exponentes negativos, multiplicamos la parte superior por$e^{2t}$ y la inferior por$\sqrt{e^{4t}}$:

\ [\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {2e^ {4t} +e^ {−2t}} {\ sqrt {e^ {4t} −e^ {−2t}}} ⋅\ dfrac {e^ {2t}} {\ sqrt {e^ {4t}}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {\ sqrt {e^ {8t} −e^ {2t}}}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {\ sqrt {e^ {2t} (e^ {6t} −1)}}\\ [4pt]
&=\ dfrac {2e^ {6t} +1} {e^t\ sqrt {e^ {6t} −1}}. \ end {alinear*}\]

Nuevamente, esta derivada también se puede calcular sustituyendo primero$x(t)$ y$f(x,y),$ luego$y(t)$ diferenciando con respecto a$t$:

$$\begin{align*} z &=f(x,y) \\[4pt] &=f(x(t),y(t)) \\[4pt] &=\sqrt{(x(t))^2−(y(t))^2} \\[4pt] &=\sqrt{e^{4t}−e^{−2t}} \\[4pt] &=(e^{4t}−e^{−2t})^{1/2}. \end{align*} \nonumber$$

Entonces

$$\begin{align*} \dfrac{dz}{dt} &= \dfrac{1}{2} (e^{4t}−e^{−2t})^{−1/2} \left(4e^{4t}+2e^{−2t} \right) \\[4pt] &=\dfrac{2e^{4t}+e^{−2t}}{\sqrt{e^{4t}−e^{−2t}}}. \end{align*}$$

Esta es la misma solución.

Ejercicio$\PageIndex{1}$

Calcular$dz/dt$ dadas las siguientes funciones. Expresar la respuesta final en términos de$t$.

$$\begin{align*} z =f(x,y) &=x^2−3xy+2y^2,\\[4pt] x =x(t) &=3\sin 2t,\\[4pt] y=y(t) &=4\cos 2t \end{align*}$$

Pista

Calcula$∂z/∂x,∂z/dy,dx/dt,$ y$dy/dt$, luego usa Ecuación\ ref {cadena1}.

Contestar

\ (\ begin {align*}\ dfrac {dz} {dt} &=\ dfrac {f} {x}\ dfrac {dx} {dt} +\ dfrac {f} {y}\ dfrac {dy} {dt}\\ [5pt]
& =( 2x−3y) (6\ cos 2t) + (−3x+4y) (−8\ sin 2t)\\ [5pt]
&=−92\ sin 2t\ cos 2t−72 (\ cos ^22t−\ sin^2 2t)\\ [5pt]
&=−46\ sin 4t−72\ cos 4t. \ end {alinear*}\)

A menudo es útil crear una representación visual de la Ecuación\ ref {cadena1} para la regla de la cadena. Esto se llama diagrama de árbol para la regla de cadena para funciones de una variable y proporciona una manera de recordar la fórmula (Figura$\PageIndex{1}$). Este diagrama se puede ampliar para funciones de más de una variable, como veremos muy pronto.

Figura$\PageIndex{1}$: Diagrama de árbol para el caso$\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}.$

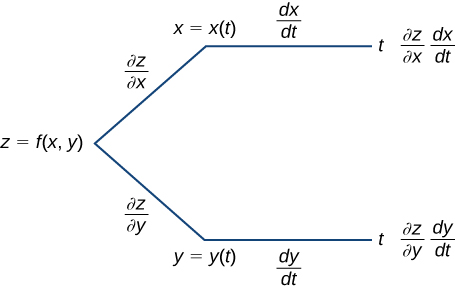
En este diagrama, la esquina más a la izquierda corresponde a$z=f(x,y)$. Ya que$f$ tiene dos variables independientes, hay dos líneas que vienen de esta esquina. La rama superior corresponde a la variable$x$ y la rama inferior corresponde a la variable$y$. Dado que cada una de estas variables es entonces dependiente de una variable$t$, entonces viene una rama$x$ y una rama viene de$y$. Por último, cada una de las ramas del extremo derecho tiene una etiqueta que representa el camino recorrido para llegar a ese ramal. A la rama superior se alcanza siguiendo la$x$ rama, luego la rama t; por lo tanto, se etiqueta$(∂z/∂x)×(dx/dt).$ La rama inferior es similar: primero la$y$ rama, luego la$t$ rama. Esta rama está etiquetada$(∂z/∂y)×(dy/dt)$. Para obtener la fórmula para$dz/dt,$ agregar todos los términos que aparecen en el lado más derecho del diagrama. Esto nos da Ecuación.

En Nota,$z=f(x,y)$ es una función de$x$ y$y$, y ambos$x=g(u,v)$ y$y=h(u,v)$ son funciones de las variables independientes$u$ y$v$.

Regla de Cadena para Dos Variables Independientes

Supongamos$x=g(u,v)$ y$y=h(u,v)$ son funciones diferenciables de$u$ y$v$, y$z=f(x,y)$ es una función diferenciable de$x$ y$y$. Entonces,$z=f(g(u,v),h(u,v))$ es una función diferenciable de$u$ y$v$, y

$$\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂u} \label{chain2a}$$

y

$$\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v}. \label{chain2b}$$

Podemos dibujar un diagrama de árbol para cada una de estas fórmulas así como sigue.

Figura$\PageIndex{2}$: Diagrama de árbol para$\dfrac{∂z}{∂u}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}$ y$\dfrac{∂z}{∂v}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}$.

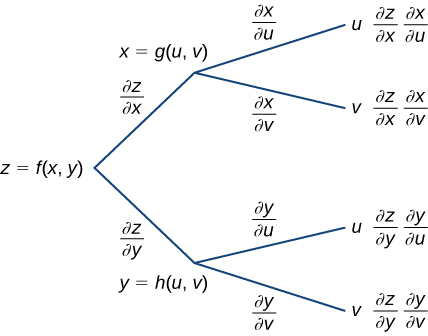
Para derivar la fórmula para$∂z/∂u$, comienza desde el lado izquierdo del diagrama, luego sigue solo las ramas con las que terminan$u$ y agrega los términos que aparecen al final de esas ramas. Para la fórmula para$∂z/∂v$, sigue solo las ramas que terminan con$v$ y agrega los términos que aparecen al final de esas ramas.

Hay una diferencia importante entre estos dos teoremas de regla de cadena. En Note, el lado izquierdo de la fórmula para la derivada no es una derivada parcial, sino que en Note lo es. La razón es que, en Note,$z$ es en última instancia una función de$t$ solo, mientras que en Note,$z$ es una función de ambos$u$ y$v$.

Ejemplo$\PageIndex{2}$: Using the Chain Rule for Two Variables

Calcular$∂z/∂u$ y$∂z/∂v$ usar las siguientes funciones:

$$z=f(x,y)=3x^2−2xy+y^2,\; x=x(u,v)=3u+2v,\; y=y(u,v)=4u−v. \nonumber$$

Solución

Para implementar la regla de la cadena para dos variables, necesitamos seis derivadas parciales,$∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,$ y$∂y/∂v$:

$$\begin{align*} \dfrac{∂z}{∂x} &=6x−2y & & \dfrac{∂z}{∂y}=−2x+2y \\[4pt] \dfrac{∂x}{∂u} &=3 & & \dfrac{∂x}{∂v}=2 \\[4pt] \dfrac{∂y}{∂u} &=4 & & \dfrac{∂y}{∂v}=−1. \end{align*}$$

Para encontrar$∂z/∂u,$ usamos la ecuación\ ref {chain2a}:

\ [\ begin {align*}\ dfrac {z} {u} &=\ dfrac {z} {x} ⋅\ dfrac {x} {u} +\ dfrac {z} {y} ⋅\ dfrac {y} {u}\\ [4pt]
&=3 (6x−2y) +4 (−2x+2y)\\ [4pt]
&=10x+2y. \ end {alinear*}\]

A continuación, sustituimos$x(u,v)=3u+2v$ y$y(u,v)=4u−v:$

$$\begin{align*} \dfrac{∂z}{∂u} &=10x+2y \\[4pt] &=10(3u+2v)+2(4u−v) \\[4pt] &=38u+18v. \end{align*}$$

Para encontrar$∂z/∂v,$ usamos la ecuación\ ref {chain2b}:

$$\begin{align*} \dfrac{∂z}{∂v} &=\dfrac{∂z}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}\dfrac{∂y}{∂v} \\[4pt] &=2(6x−2y)+(−1)(−2x+2y) \\[4pt] &=14x−6y. \end{align*}$$

Luego sustituimos$x(u,v)=3u+2v$ y$y(u,v)=4u−v:$

$$\begin{align*} \dfrac{∂z}{∂v} &=14x−6y \\[4pt] &=14(3u+2v)−6(4u−v) \\[4pt] &=18u+34v \end{align*}$$

Ejercicio$\PageIndex{2}$

Calcular$∂z/∂u$ y$∂z/∂v$ dadas las siguientes funciones:

$$z=f(x,y)=\dfrac{2x−y}{x+3y},\quad x(u,v)=e^{2u}\cos 3v,\quad y(u,v)=e^{2u}\sin 3v. \nonumber$$

Pista

Calcula$∂z/∂x,\; ∂z/∂y,\; ∂x/∂u,\; ∂x/∂v,\; ∂y/∂u,$ y$∂y/∂v$, luego usa la Ecuación\ ref {cadena2a} y la Ecuación\ ref {cadena2b}.

Contestar

$\dfrac{∂z}{∂u}=0,\quad \dfrac{∂z}{∂v}=\dfrac{−21}{(3\sin 3v+\cos 3v)^2}$

La regla de la cadena generalizada

Ahora que hemos visto cómo extender la regla de cadena original a funciones de dos variables, es natural preguntarse: ¿Podemos extender la regla a más de dos variables? La respuesta es sí, como afirma la regla de la cadena generalizada.

Regla de Cadena Generalizada

Dejar$w=f(x_1,x_2,…,x_m)$ ser una función diferenciable de variables$m$ independientes, y para cada una$i∈{1,…,m},$ dejar$x_i=x_i(t_1,t_2,…,t_n)$ ser una función diferenciable de variables$n$ independientes. Entonces

$$\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_2}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j} \nonumber$$

para cualquier$j∈{1,2,…,n}.$

En el siguiente ejemplo calculamos la derivada de una función de tres variables independientes en las que cada una de las tres variables depende de otras dos variables.

Ejemplo$\PageIndex{3}$: Using the Generalized Chain Rule

Calcular$∂w/∂u$ y$∂w/∂v$ usar las siguientes funciones:

$$\begin{align*} w &=f(x,y,z)=3x^2−2xy+4z^2 \\[4pt] x &=x(u,v)=e^u\sin v \\[4pt] y &=y(u,v)=e^u\cos v \\[4pt] z &=z(u,v)=e^u. \end{align*}$$

Solución

Las fórmulas para$∂w/∂u$ y$∂w/∂v$ son

$$\begin{align*} \dfrac{∂w}{∂u} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} =\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v}. \end{align*}$$

Por lo tanto, hay nueve derivadas parciales diferentes que necesitan ser calculadas y sustituidas. Necesitamos calcular cada uno de ellos:

$$\begin{align*} \dfrac{∂w}{∂x}&=6x−2y \dfrac{∂w}{∂y}=−2x \dfrac{∂w}{∂z}=8z \\[4pt] \dfrac{∂x}{∂u}&=e^u\sin v \dfrac{∂y}{∂u}=e^u\cos v \dfrac{∂z}{∂u}=e^u \\[4pt] \dfrac{∂x}{∂v}&=e^u\cos v \dfrac{∂y}{∂v}=−e^u\sin v \dfrac{∂z}{∂v}=0. \end{align*}$$

Ahora, sustituimos cada uno de ellos en la primera fórmula para calcular$∂w/∂u$:

\ [\ begin {align*}\ dfrac {w} {u} &=\ dfrac {w} {x} ⋅\ dfrac {x} {u} +\ dfrac {w} {y} ⋅\ dfrac {y} {u} +\ dfrac {w} {z} ⋅\ dfrac {z} ⋅\ dfrac {z} ⋅ dfrac {z}} {u}\\ [4pt]
& =( 6x−2y) e^u\ sin v−2xe^u\ cos v+8ze^u,\ end {align*}\]

luego sustituya$x(u,v)=e^u \sin v, \, y(u,v)=e^u\cos v,$ y$z(u,v)=e^u$ en esta ecuación:

$$\begin{align*} \dfrac{∂w}{∂u} &=(6x−2y)e^u\sin v−2xe^u\cos v+8ze^u \\[4pt] &=(6e^u\sin v−2eu\cos v)e^u\sin v−2(e^u\sin v)e^u\cos v+8e^{2u} \\[4pt] &=6e^{2u}\sin^2 v−4e^{2u}\sin v\cos v+8e^{2u} \\[4pt] &=2e^{2u}(3\sin^2 v−2\sin v\cos v+4). \end{align*}$$

A continuación, calculamos$∂w/∂v$:

$$\begin{align*} \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}⋅\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}⋅\dfrac{∂z}{∂v} \\[4pt] &=(6x−2y)e^u\cos v−2x(−e^u\sin v)+8z(0), \end{align*}$$

entonces sustituimos$x(u,v)=e^u\sin v,\, y(u,v)=e^u\cos v,$ y$z(u,v)=e^u$ en esta ecuación:

$$\begin{align*} \dfrac{∂w}{∂v} &=(6x−2y)e^u\cos v−2x(−e^u\sin v) \\[4pt] &=(6e^u \sin v−2e^u\cos v)e^u\cos v+2(e^u\sin v)(e^u\sin v) \\[4pt] &=2e^{2u}\sin^2 v+6e^{2u}\sin v\cos v−2e^{2u}\cos^2 v \\[4pt] &=2e^{2u}(\sin^2 v+\sin v\cos v−\cos^2 v). \end{align*}$$

Ejercicio$\PageIndex{3}$

Calcular$∂w/∂u$ y$∂w/∂v$ dadas las siguientes funciones:

$$\begin{align*} w &=f(x,y,z)=\dfrac{x+2y−4z}{2x−y+3z} \\[4pt] x &=x(u,v)=e^{2u}\cos3v \\[4pt] y &=y(u,v)=e^{2u}\sin 3v \\[4pt] z &=z(u,v)=e^{2u}. \end{align*}$$

Pista

Calcula nueve derivadas parciales, luego usa las mismas fórmulas de Ejemplo$\PageIndex{3}$.

Contestar

$\dfrac{∂w}{∂u}=0$

$\dfrac{∂w}{∂v}=\dfrac{15−33\sin 3v+6\cos 3v}{(3+2\cos 3v−\sin 3v)^2}$

Ejemplo$\PageIndex{4}$: Drawing a Tree Diagram

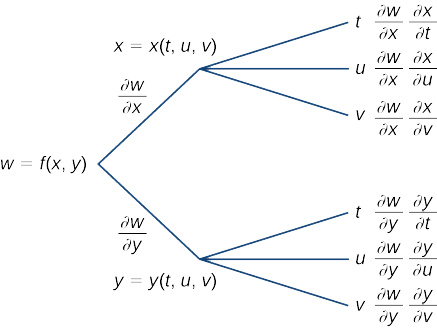
Crear un diagrama de árbol para el caso cuando

$$w=f(x,y,z),\quad x=x(t,u,v),\quad y=y(t,u,v),\quad z=z(t,u,v) \nonumber$$

y escribir las fórmulas para las tres derivadas parciales de$w$.

Solución

A partir de la izquierda, la función$f$ tiene tres variables independientes:$x,\, y$, y$z$. Por lo tanto, tres ramas deben estar emanando del primer nodo. Cada una de estas tres ramas también tiene tres ramas, para cada una de las variables$t,\, u,$ y$v$.

Figura$\PageIndex{3}$: Diagrama de árbol para una función de tres variables, cada una de las cuales es una función de tres variables independientes.

Las tres fórmulas son

$$\begin{align*} \dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v}+\dfrac{∂w}{∂z}\dfrac{∂z}{∂v}. \end{align*}$$

Ejercicio$\PageIndex{4}$

Crear un diagrama de árbol para el caso cuando

$$w=f(x,y),\quad x=x(t,u,v),\quad y=y(t,u,v) \nonumber$$

y escribir las fórmulas para las tres derivadas parciales de$w.$

Pista

Determinar el número de ramas que emanan de cada nodo en el árbol.

Contestar

$$\begin{align*}\dfrac{∂w}{∂t} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂t}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂t} \\[4pt] \dfrac{∂w}{∂u} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂u}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂u} \\[4pt] \dfrac{∂w}{∂v} &=\dfrac{∂w}{∂x}\dfrac{∂x}{∂v}+\dfrac{∂w}{∂y}\dfrac{∂y}{∂v} \end{align*}$$

Diferenciación implícita

Recordar de la diferenciación implícita proporciona un método para encontrar$dy/dx$ cuándo$y$ se define implícitamente como una función de$x$. El método implica diferenciar ambos lados de la ecuación definiendo la función con respecto a$x$, luego resolver para Derivadas$dy/dx.$ parciales proporcionan una alternativa a este método.

Considera la elipse definida por la ecuación de la$x^2+3y^2+4y−4=0$ siguiente manera.

Figura$\PageIndex{4}$: Gráfico de la elipse definida por$x^2+3y^2+4y−4=0$.

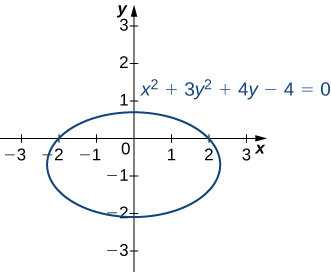
Esta ecuación define implícitamente$y$ como una función de$x$. Como tal, podemos encontrar la derivada$dy/dx$ utilizando el método de diferenciación implícita:

$$\begin{align*} \dfrac{d}{dx}(x^2+3y^2+4y−4) &=\dfrac{d}{dx}(0) \\[4pt] 2x+6y\dfrac{dy}{dx}+4\dfrac{dy}{dx} &=0 \\[4pt] (6y+4)\dfrac{dy}{dx} &=−2x\\[4pt] \dfrac{dy}{dx} &=−\dfrac{x}{3y+2}\end{align*}$$

También podemos definir una función$z=f(x,y)$ usando el lado izquierdo de la ecuación que define la elipse. Entonces$f(x,y)=x^2+3y^2+4y−4.$ La elipse$x^2+3y^2+4y−4=0$ puede entonces ser descrita por la ecuación$f(x,y)=0$. El uso de esta función y el siguiente teorema nos da un enfoque alternativo para calcular$dy/dx.$

Teorema: Diferenciación implícita de una función de dos o más variables

Supongamos que la función$z=f(x,y)$ define$y$ implícitamente como una función$y=g(x)$ de$x$ vía la ecuación$f(x,y)=0.$ Entonces

$$\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y} \label{implicitdiff1}$$

siempre$f_y(x,y)≠0.$

Si la ecuación$f(x,y,z)=0$ define$z$ implícitamente como una función diferenciable de$x$ y$y$, entonces

$$\dfrac{dz}{dx}=−\dfrac{∂f/∂x}{∂f/∂z} \qquad\text{and}\qquad \dfrac{dz}{dy}=−\dfrac{∂f/∂y}{∂f/∂z}\label{implicitdiff2}$$

siempre y cuando$f_z(x,y,z)≠0.$

La ecuación\ ref {implicitdiff1} es una consecuencia directa de la ecuación\ ref {chain2a}. En particular, si asumimos que$y$ se define implícitamente como una función de$x$ vía la ecuación$f(x,y)=0$, podemos aplicar la regla de la cadena para encontrar$dy/dx:$

$$\begin{align*} \dfrac{d}{dx}f(x,y) &=\dfrac{d}{dx}(0) \\[4pt] \dfrac{∂f}{∂x}⋅\dfrac{dx}{dx}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0 \\[4pt]\dfrac{∂f}{∂x}+\dfrac{∂f}{∂y}⋅\dfrac{dy}{dx} &=0. \end{align*}$$

Resolviendo esta ecuación para$dy/dx$ da Ecuación\ ref {implicitdiff1}. La ecuación\ ref {implicitdiff1} se puede derivar de manera similar.

Volvamos ahora al problema que iniciamos antes del teorema anterior. Usando Note y la función$f(x,y)=x^2+3y^2+4y−4,$ que obtenemos

$$\begin{align*} \dfrac{∂f}{∂x} &=2x\\[4pt] \dfrac{∂f}{∂y} &=6y+4. \end{align*}$$

Entonces la ecuación\ ref {implicitdiff1} da

$$\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=−\dfrac{2x}{6y+4}=−\dfrac{x}{3y+2}, \nonumber$$

que es el mismo resultado obtenido por el uso anterior de la diferenciación implícita.

Ejemplo$\PageIndex{5}$: Implicit Differentiation by Partial Derivatives

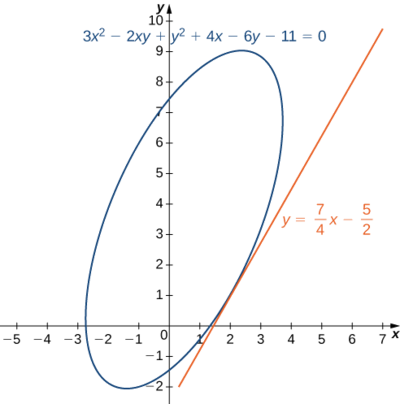
1. Calcular$dy/dx$ si$y$ se define implícitamente como una función de$x$ vía la ecuación$3x^2−2xy+y^2+4x−6y−11=0$. ¿Cuál es la ecuación de la línea tangente a la gráfica de esta curva en el punto$(2,1)$?
2. Calcular$∂z/∂x$ y$∂z/∂y,$ dado$x^2e^y−yze^x=0.$

Solución

a. Establecer$f(x,y)=3x^2−2xy+y^2+4x−6y−11=0,$ luego calcular$f_x$ y$f_y: f_x(x,y)=6x−2y+4$ y$f_y(x,y)=−2x+2y−6.$

La derivada viene dada por

$$\dfrac{dy}{dx}=−\dfrac{∂f/∂x}{∂f/∂y}=\dfrac{6x−2y+4}{−2x+2y−6}=\dfrac{3x−y+2}{x−y+3}. \nonumber$$

La pendiente de la línea tangente en el punto$(2,1)$ viene dada por

$$\dfrac{dy}{dx}\Bigg|_{(x,y)=(2,1)}=\dfrac{3(2)−1+2}{2−1+3}=\dfrac{7}{4} \nonumber$$

Para encontrar la ecuación de la línea tangente, utilizamos la forma punto-pendiente (Figura$\PageIndex{5}$):

$$\begin{align*} y−y_0 &=m(x−x_0)\\[4pt]y−1 &=\dfrac{7}{4}(x−2) \\[4pt] y &=\dfrac{7}{4}x−\dfrac{7}{2}+1\\[4pt] y &=\dfrac{7}{4}x−\dfrac{5}{2}.\end{align*}$$

Figura$\PageIndex{5}$: Gráfico de la elipse rotada definida por$3x^2−2xy+y^2+4x−6y−11=0$.

b. Tenemos$f(x,y,z)=x^2e^y−yze^x.$ Por lo tanto,

$$\begin{align*} \dfrac{∂f}{∂x} &=2xe^y−yze^x \\[4pt] \dfrac{∂f}{∂y} &=x^2e^y−ze^x \\[4pt] \dfrac{∂f}{∂z} &=−ye^x\end{align*}$$

Usando la ecuación\ ref {implicitdiff2},

$$\begin{align*} \dfrac{∂z}{∂x} &=−\dfrac{∂f/∂x}{∂f/∂y} & &\text{and} & \dfrac{∂z}{∂y} =−\dfrac{∂f/∂y}{∂f/∂z} \\[4pt] &=−\dfrac{2xe^y−yze^x}{−ye^x} & & &=−\dfrac{x^2e^y−ze^x}{−ye^x} \\[4pt] &=\dfrac{2xe^y−yze^x}{ye^x} & & & =\dfrac{x^2e^y−ze^x}{ye^x} \end{align*}$$

Ejercicio$\PageIndex{5}$

Encontrar$dy/dx$ si$y$ se define implícitamente como una función de$x$ por la ecuación$x^2+xy−y^2+7x−3y−26=0$. ¿Cuál es la ecuación de la línea tangente a la gráfica de esta curva en el punto$(3,−2)$?

Pista

Calcular$∂f/dx$ y$∂f/dy$, a continuación, utilizar la ecuación\ ref {implicitdiff1}.

Solución

$$\dfrac { d y } { d x } = \left. \frac { 2 x + y + 7 } { 2 y - x + 3 } \right| _ { ( 3 , - 2 ) } = \dfrac { 2 ( 3 ) + ( - 2 ) + 7 } { 2 ( - 2 ) - ( 3 ) + 3 } = - \dfrac { 11 } { 4 } \nonumber$$

Ecuación de la línea tangente:$y=−\dfrac{11}{4}x+\dfrac{25}{4}$

Conceptos clave

• La regla de cadena para funciones de más de una variable involucra las derivadas parciales con respecto a todas las variables independientes.
• Los diagramas de árbol son útiles para derivar fórmulas para la regla de cadena para funciones de más de una variable, donde cada variable independiente también depende de otras variables.

Ecuaciones Clave

• Regla de cadena, una variable independiente

$\dfrac{dz}{dt}=\dfrac{∂z}{∂x}⋅\dfrac{dx}{dt}+\dfrac{∂z}{∂y}⋅\dfrac{dy}{dt}$

• Regla de cadena, dos variables independientes

$\dfrac{dz}{du}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂u}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂u}\dfrac{dz}{dv}=\dfrac{∂z}{∂x}⋅\dfrac{∂x}{∂v}+\dfrac{∂z}{∂y}⋅\dfrac{∂y}{∂v}$

• Regla de cadena generalizada

$\dfrac{∂w}{∂t_j}=\dfrac{∂w}{∂x_1}\dfrac{∂x_1}{∂t_j}+\dfrac{∂w}{∂x_2}\dfrac{∂x_1}{∂t_j}+⋯+\dfrac{∂w}{∂x_m}\dfrac{∂x_m}{∂t_j}$

Glosario

regla de cadena generalizada

la regla de cadena extendida a funciones de más de una variable independiente, en la que cada variable independiente puede depender de una o más de otras variables

variable intermedia

dada una composición de funciones (por ejemplo$f(x(t),y(t)))$, las variables intermedias son las variables que son independientes en la función externa pero también dependientes de otras variables; en la función$f(x(t),y(t)),$ las variables$x$ y$y$ son ejemplos de variables intermedias

diagrama de árbol

ilustra y deriva fórmulas para la regla de cadena generalizada, en la que se contabiliza cada variable independiente