3.1: Valores extremos
- Page ID
- 111774
Nuestro estudio de los límites condujo a funciones continuas, que es una cierta clase de funciones que se comportan de una manera particularmente agradable. Los límites nos dieron entonces una clase de funciones aún más agradable, funciones que son diferenciables.
Este capítulo explora muchas de las formas en que podemos aprovechar la información que proporcionan las funciones continuas y diferenciables.
Dada cualquier cantidad descrita por una función, a menudo nos interesan los valores más grandes y/o menores que alcanza la cantidad. Por ejemplo, si una función describe la velocidad de un objeto, parece razonable querer saber lo más rápido/más lento que viajó el objeto. Si una función describe el valor de una acción, es posible que queramos saber cómo los valores más altos/más bajos alcanzaron las acciones en el último año. A tales valores los llamamos valores extremos.
Definición\(\PageIndex{1}\): Minima and Maxima
Dejar\(f\) ser definido en un intervalo\(I\) que contiene\(c\).
- \(f(c)\)es el mínimo (también, mínimo absoluto) de\(f\) on\(I\) si\(f(c) \leq f(x)\) para todos\(x\) en\(I\).
- \(f(c)\)es el máximo} (también, máximo absoluto) de\(f\) on\(I\) si\(f(c) \geq f(x)\) para todos\(x\) en\(I\).
Los valores máximo y mínimo son los valores extremos, o extremos, de\(f\) on\(I\).
Los valores extremos de una función son valores\(y\) "", valores que obtiene la función, no los valores de entrada.
Considera Figura\(\PageIndex{1}\). La función mostrada en (a) tiene un máximo, pero no mínimo, ya que el intervalo sobre el que se define la función está abierto. En (b), la función tiene un mínimo, pero no máximo; hay una discontinuidad en el lugar “natural” para que ocurra el máximo. Finalmente, la función mostrada en (c) tiene tanto un máximo como un mínimo; tenga en cuenta que la función es continua y el intervalo en el que se define está cerrado.
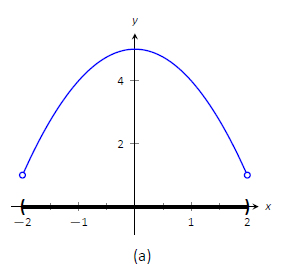
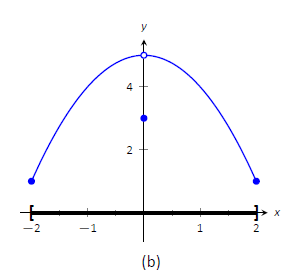
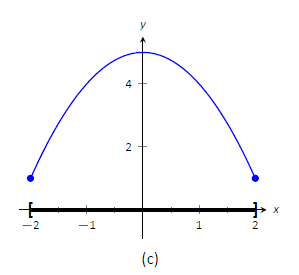
Figura\(\PageIndex{1}\): Gráficas de funciones con y sin valores extremos
Es posible que las funciones discontinuas definidas en un intervalo abierto tengan tanto un valor máximo como mínimo, pero acabamos de ver ejemplos donde no lo hicieron. Por otro lado, las funciones continuas en un intervalo cerrado siempre tienen un valor máximo y mínimo.
Teorema\(\PageIndex{1}\): The Extreme Value Theorem
Let\(f\) Ser una función continua definida en un intervalo cerrado\(I\). Entonces\(f\) tiene tanto un valor máximo como mínimo on\(I\).
Este teorema afirma que\(f\) tiene valores extremos, pero no ofrece ningún consejo sobre cómo/dónde encontrar estos valores. El proceso puede parecer bastante fácil, como lo ilustra el siguiente ejemplo. Después del ejemplo, aprovecharemos las lecciones aprendidas para formar un método más general y poderoso para encontrar valores extremos.
Ejemplo\(\PageIndex{1}\): Approximating Extreme Values
\(f(x) = 2x^3-9x^2\)Considerar\(I=[-1,5]\), como se grafica en la Figura\(\PageIndex{2}\). Aproximar los valores extremos de\(f\).
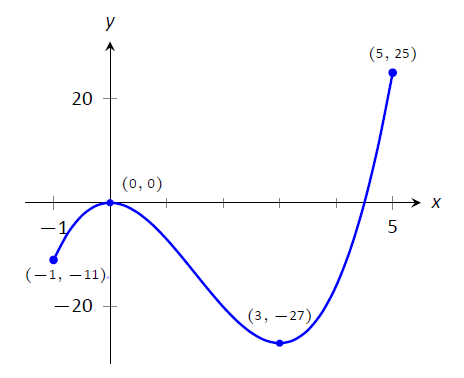
Figura\(\PageIndex{2}\): Un gráfico de\(f(x) = 2x^3-9x^2\) como en el Ejemplo\(\PageIndex{1}\)
Solución
El gráfico se dibuja de tal manera que llame la atención sobre ciertos puntos. Ciertamente parece que el\(y\) valor más pequeño es\(-27\), que se encuentra cuando\(x=3\). También parece que el\(y\) valor más grande es 25, encontrado en el punto final de\(I\),\(x=5\). Usamos la palabra parece, pues solo por la gráfica no podemos estar seguros de que el valor más pequeño no sea menor que\(-27\). Dado que el problema pide una aproximación, aproximamos los valores extremos a ser\(25\) y\(-27\).
Observe cómo el valor mínimo llegó al “fondo de una colina”, y el valor máximo llegó a un punto final. También tenga en cuenta que si bien no\(0\) es un valor extremo, lo sería si redujéramos nuestro intervalo a\([-1,4]\). Es importante la idea de que el punto\((0,0)\) es la ubicación de un valor extremo para algún intervalo, llevándonos a una definición.
Extrema Local y Relativa
Los términos mínimo local y máximo local se utilizan a menudo como sinónimos de mínimo relativo y máximo relativo. Practicamos brevemente el uso de estas definiciones.
Definición\(\PageIndex{2}\): Relative Minimum and Relative Maximum
Dejar\(f\) ser definido en un intervalo\(I\) que contiene\(c\).
- Si hay un intervalo abierto que contiene\(c\) tal que\(f(c)\) es el valor mínimo, entonces\(f(c)\) es un mínimo relativo de\(f\). También decimos que\(f\) tiene un mínimo relativo en\((c,f(c))\).
- Si hay un intervalo abierto que contiene\(c\) tal que\(f(c)\) es el valor máximo, entonces\(f(c)\) es un máximo relativo de\(f\). También decimos que\(f\) tiene un máximo relativo en\((c,f(c))\).
Los valores máximos y mínimos relativos comprenden los extremos relativos de\(f\).
Ejemplo\(\PageIndex{2}\): Approximating Relative Extrema
Considere\(f(x) = (3x^4-4x^3-12x^2+5)/5\), como se muestra en la Figura\(\PageIndex{3}\). Aproximar los extremos relativos de\(f\). En cada uno de estos puntos, evaluar\(f'\).
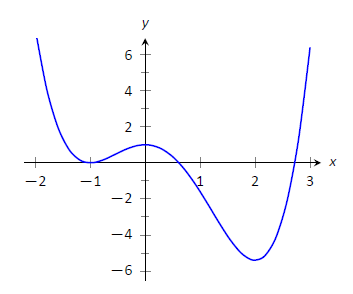
Figura\(\PageIndex{3}\): Una gráfica de\(f(x) = (3x^4-4x^3-12x^2+5)/5\) como en el Ejemplo\(\PageIndex{2}\).
Solución
Todavía no tenemos las herramientas para encontrar exactamente los extremos relativos, pero la gráfica sí nos permite hacer aproximaciones razonables. Parece que\(f\) tiene mínimos relativos en\(x=-1\) y\(x=2\), con valores de\(f(-1)=0\) y\(f(2) = -5.4\). También parece que\(f\) tiene un máximo relativo en el punto\((0,1)\).
Aproximamos los mínimos relativos a ser\(0\) y\(-5.4\); aproximamos el máximo relativo a ser\(1\).
Es sencillo evaluar\(f'(x) =\frac15(12x^3-12x^2-24x)\) en\(x=0, 1\) y\(2\). En cada caso,\(f'(x) = 0\).
Ejemplo\(\PageIndex{3}\): Approximating Relative Extrema
Aproximar los extremos relativos de\(f(x) = (x-1)^{2/3}+2\), mostrados en la Figura\(\PageIndex{4}\). En cada uno de estos puntos, evaluar\(f'\).
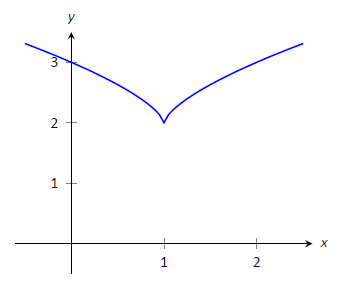
Figura\(\PageIndex{4}\): Una gráfica de\(f(x) = (x-1)^{2/3}+2\) como en el Ejemplo\(\PageIndex{3}\).
Solución
La cifra implica que\(f\) no tiene ningún máximo relativo, sino que tiene un mínimo relativo en\((1,2)\). De hecho, la gráfica sugiere que no sólo este punto es un mínimo relativo,\(y=f(1)=2\) el valor mínimo de la función.
Nosotros computamos\(f'(x) = \frac{2}{3}(x-1)^{-1/3}\). Cuando\(x=1\),\(f'\) es indefinido.
¿Qué podemos aprender de los dos ejemplos anteriores? Pudimos aproximar visualmente los extremos relativos, y en cada uno de esos puntos, la derivada fue\(0\) o no se definió. Esta observación se sostiene para todas las funciones, lo que lleva a una definición y un teorema.
Definición\(\PageIndex{3}\): Critical Numbers and Critical Points
Dejar\(f\) ser definido en\(c\). El valor\(c\) es un número crítico (o valor crítico) de\(f\) si\(f'(c)=0\) o no\(f'(c)\) está definido.
Si\(c\) es un número crítico de\(f\), entonces el punto\((c,f(c))\) es un punto crítico de\(f\).
Teorema\(\PageIndex{1}\): Relative Extrema and Critical Points
Dejar que una función\(f\) tenga un extremo relativo en el punto\((c,f(c))\). Entonces\(c\) es un número crítico de\(f\).
Tenga cuidado de entender que este teorema afirma “Todos los extremos relativos ocurren en puntos críticos”. No dice “Todos los números críticos producen extremos relativos”. Por ejemplo, considere\(f(x) = x^3\). Ya que\(f'(x) = 3x^2\), es sencillo determinar que\(x=0\) es un número crítico de\(f\). Sin embargo, no\(f\) tiene extremos relativos, como se ilustra en la Figura\(\PageIndex{5}\).
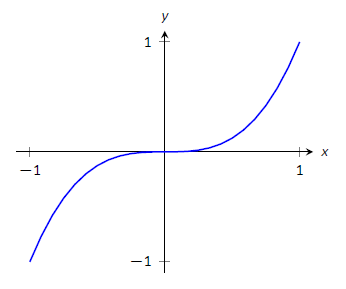
Figura\(\PageIndex{5}\): Una gráfica de la\(f(x)=x^3\) cual tiene un valor crítico de\(x=0\), pero ningún extremo relativo.
El teorema\(\PageIndex{1}\) afirma que una función continua en un intervalo cerrado tendrá extremos absolutos, es decir, tanto un máximo absoluto como un mínimo absoluto. Estos extremos ocurren ya sea en los puntos finales o en valores críticos en el intervalo. Combinamos estos conceptos para ofrecer una estrategia para encontrar extremos.
Idea Clave 2: Encontrar Extremos en un Intervalo Cerrado
Let\(f\) Ser una función continua definida en un intervalo cerrado\([a,b]\). Para encontrar los valores máximos y mínimos de\(f\) on\([a,b]\)
- Evaluar\(f\) en los puntos finales\(a\) y\(b\) del intervalo.
- Encuentre los números críticos de\(f\) in\([a,b]\).
- Evaluar\(f\) en cada número crítico.
- El máximo absoluto de\(f\) es el mayor de estos valores, y el mínimo absoluto de\(f\) es el menor de estos valores.
Practicamos estas ideas en los siguientes ejemplos.
Ejemplo\(\PageIndex{4}\): Finding Extreme Values
Encuentra los valores extremos de\(f(x) = 2x^3+3x^2-12x\) on\([0,3]\), graficados en la Figura\(\PageIndex{6}\).
Seguimos los pasos descritos en la Idea Clave 2. Primero evaluamos\(f\) en los puntos finales:
\[f(0) = 0 \quad \text{and}\quad f(3) =45.\]
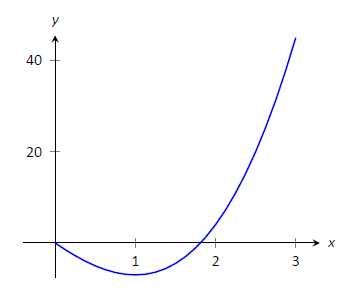
Figura\(\PageIndex{6}\): Una gráfica de\(f(x) = 2x^3+3x^2-12x\) on\([0,3]\) como en el Ejemplo\(\PageIndex{4}\).
A continuación, encontramos los valores críticos de\(f\) on\([0,3]\). \(f'(x) = 6x^2+6x-12 = 6(x+2)(x-1)\); por lo tanto, los valores críticos de\(f\) son\(x=-2\) y\(x=1\). Ya que\(x=-2\) no se encuentra en el intervalo\([0,3]\), lo ignoramos. Evaluar\(f\) en el único número crítico en nuestro intervalo da:\(f(1) = -7\).
Tabla\(\PageIndex{1}\) da\(f\) evaluados a los\(x\) valores “importantes” en\([0,3]\). Podemos ver fácilmente los valores máximo y mínimo de\(f\): el valor máximo es\(45\) y el valor mínimo es\(-7\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">0 | \ (f (x)\) ">0 |
| \ (x\) ">1 | \ (f (x)\) ">-7 |
| \ (x\) ">3 | \ (f (x)\) ">45 |
Tenga en cuenta que todo esto se hizo sin la ayuda de una gráfica; este trabajo siguió un algoritmo analítico y no dependió de ninguna visualización. La figura\(\PageIndex{6}\) muestra\(f\) y podemos confirmar nuestra respuesta, pero es importante entender que estas respuestas se pueden encontrar sin asistencia gráfica.
Volvemos a practicar.
Ejemplo\(\PageIndex{5}\): Finding Extreme Values
Encuentra los valores máximos y mínimos de\(f\) on\([-4,2]\), donde
\[f(x) = \left\{\begin{array}{cc} (x-1)^2 & x\leq 0 \\ x+1 & x>0 \end{array}\right. .\]
Solución
Aquí\(f\) está definido poco a poco, pero aún podemos aplicar la Idea Clave 2. Evaluar\(f\) en los puntos finales da:
\[ f(-4) = 25 \quad \text{and} \quad f(2) = 3.\]
Ahora nos encontramos con los números críticos de\(f\). Tenemos que definir\(f'\) de manera fragmentaria; es
\[f'(x) =\left\{\begin{array}{cc} 2(x-1) & x < 0 \\ 1 & x>0 \end{array}\right. .\]
Tenga en cuenta que si bien\(f\) se define para todos\([-4,2]\), no lo\(f'\) es, ya que la derivada de\(f\) no existe cuando\(x=0\). (Desde la izquierda, la derivada se aproxima\(-2\); desde la derecha la derivada es 1.) Por lo tanto, un número crítico de\(f\) es\(x=0\).
Ahora nos fijamos\(f'(x) = 0\). Cuando\(x >0\), nunca\(f'(x)\) es 0. Cuando\(x<0\), tampoco\(f'(x)\) es nunca 0. (Podemos estar tentados a decir eso\(f'(x) = 0 \) cuando\(x=1\). No obstante, esto no tiene sentido, pues solo consideramos\(f'(x) = 2(x-1)\) cuándo\(x<0\), entonces ignoraremos una solución que diga\(x=1\).)
Entonces tenemos tres\(x\) valores importantes a considerar:\(x= -4, 2\) y\(0\). Evaluando\(f\) en cada da, respectivamente,\(25\),\(3\) y\(1\), se muestra en la Tabla\(\PageIndex{2}\). Así el mínimo absoluto de\(f\) es 1; el máximo absoluto de\(f\) es\(25\). Nuestra respuesta es confirmada por la gráfica de\(f\) en la Figura\(\PageIndex{7}\).
| \(x\) | \(f(x)\) |
| -4 | 25 |
| 0 | 1 |
| 2 | 3 |
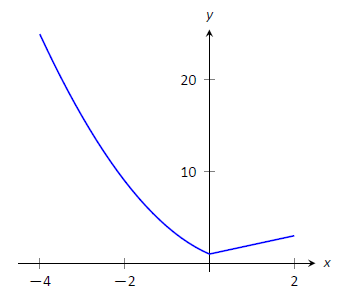
Figura\(\PageIndex{7}\): Una gráfica de\(f(x)\) on\([-4,2]\) como en el Ejemplo\(\PageIndex{5}\).
Ejemplo\(\PageIndex{6}\): Finding Extreme Values
Encuentra los extremos de\(f(x) = \cos (x^2)\) on\([-2,2]\).
Solución
Nuevamente usamos Key Idea 3. Evaluar\(f\) en los puntos finales del intervalo da: Ahora\(f(-2) = f(2) = \cos (4) \approx -0.6536.\) encontramos los valores críticos de\(f\).
Aplicando la Regla de la Cadena, nos encontramos\(f'(x) = -2x\sin (x^2)\). Establecer\(f'(x) = 0\) y resolver\(x\) para encontrar los valores críticos de\(f\).
Tenemos\(f'(x) = 0\) cuándo\(x = 0\) y cuándo\(\sin (x^2) = 0\). En general,\(\sin t = 0\) cuando\(t = \ldots -2\pi, -\pi, 0, \pi, \ldots\) Así\(\sin (x^2) = 0\) cuando\(x^2 = 0, \pi, 2\pi, \ldots\) (siempre\(x^2\) es positivo así que ignoramos\(-\pi\), etc.) Entonces,\(\sin (x^2)=0\) cuando\(x= 0, \pm \sqrt{\pi}, \pm\sqrt{2\pi}, \ldots\). Los únicos valores a caer en el intervalo dado\([-2,2]\) son\(-\sqrt{\pi}\) y\(\sqrt{\pi}\), aproximadamente\(\pm 1.77\).
Nuevamente construimos una tabla de valores importantes en Table\(\PageIndex{3}\). En este ejemplo tenemos 5 valores a considerar:\(x= 0, \pm 2, \pm\sqrt{\pi}\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">-2 | \ (f (x)\) ">-0.65 |
| \ (x\) ">\(-\sqrt{\pi}\) | \ (f (x)\) ">-1 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">\(\sqrt{\pi}\) | \ (f (x)\) ">-1 |
| \ (x\) ">2 | \ (f (x)\) ">-0.65 |
De la tabla queda claro que el valor máximo de\(f\) on\([-2,2]\) es 1; el valor mínimo es\(-1\). La gráfica de la Figura\(\PageIndex{8}\) confirma nuestros resultados.
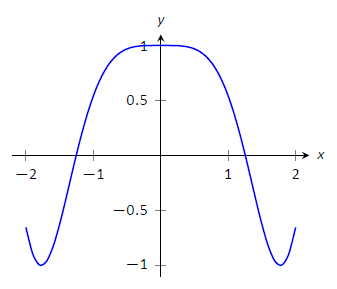
Figura\(\PageIndex{8}\): Una gráfica de\(f(x)=\cos(x^2)\) on\([-2,2]\) como en el Ejemplo\(\PageIndex{5}\).
Consideramos un ejemplo más.
Ejemplo\(\PageIndex{7}\): Finding Extreme Values
Encuentra los valores extremos de\(f(x) = \sqrt{1-x^2}\).
Solución
No se da un intervalo cerrado, por lo que encontramos los valores extremos de\(f\) en su dominio. \(f\)se define siempre que\(1-x^2\geq 0\); así el dominio de\(f\) es\([-1,1]\). Evaluar\(f\) en cualquiera de los puntos finales devuelve\(0\).
Usando la Regla de la Cadena, encontramos\(f'(x) = \frac{-x}{\sqrt{1-x^2}}\). Los puntos críticos de\(f\) se encuentran cuando\(f'(x) = 0\) o cuando\(f'\) está indefinido. Es sencillo encontrar que\(f'(x) = 0\) cuando\(x=0\), y\(f'\) es indefinido cuando\(x=\pm 1\), los puntos finales del intervalo. La tabla de valores importantes se da en la Tabla\(\PageIndex{4}\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">-1 | \ (f (x)\) ">0 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">1 | \ (f (x)\) ">0 |
El valor máximo es 1, y el valor mínimo es 0.
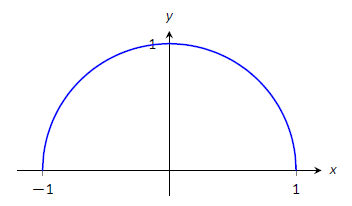
Figura\(\PageIndex{9}\): Una gráfica de\(f(x)=\sqrt{1-x^2}\) on\([-1,1]\) como en el Ejemplo\(\PageIndex{7}\)
Nota: Se encontró implícitamente la derivada de\(x^2+y^2=1\), el círculo unitario, en la sección de Diferenciación Implícita como\(\frac{dy}{dx} = -x/y\). En Ejemplo\(\PageIndex{7}\), la mitad del círculo unitario se da como\(y=f(x) = \sqrt{1-x^2}\). Encontramos\(f'(x) = \frac{-x}{\sqrt{1-x^2}}\). Reconocer que el denominador de esta fracción es\(y\); es decir, nuevamente encontramos\(f'(x) = \frac{dy}{dx} = -x/y.\)
Hemos visto que las funciones continuas en intervalos cerrados siempre tienen un valor máximo y mínimo, y también hemos desarrollado una técnica para encontrar estos valores. En la siguiente sección, profundizamos nuestro estudio de la información que podemos extraer de las funciones “agradables” con el Teorema del Valor Medio. En un intervalo cerrado, podemos encontrar la tasa promedio de cambio de una función (como lo hicimos al inicio del Capítulo 2). Veremos que las funciones diferenciables siempre tienen un punto en el que su tasa instantánea de cambio es la misma que la tasa promedio de cambio. Esto es sorprendentemente útil, como veremos.


