4.2: Tarifas Relacionadas

Última actualización
Guardar como PDF

Page ID: 111765

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Cuando dos cantidades están relacionadas por una ecuación, conocer el valor de una cantidad puede determinar el valor de la otra. Por ejemplo, la circunferencia y el radio de un círculo están relacionados por$C=2\pi r$; sabiendo que$C = 6\pi$ en determina el radio debe ser de 3 pulgadas.

El tema de las tarifas relacionadas lleva esto un paso más allá: conocer la tasa a la que está cambiando una cantidad puede determinar la tasa a la que cambia la otra.

Nota: Esta sección se basa en gran medida en la diferenciación implícita, por lo que remitirse a la Sección 2.6 puede ayudar. Demostramos los conceptos de tasas relacionadas a través de ejemplos.

Ejemplo$\PageIndex{1}$: Understanding related rates

El radio de un círculo está creciendo a una velocidad de 5 in/hr. ¿A qué ritmo crece la circunferencia?

Solución

La circunferencia y el radio de un círculo están relacionados por$C = 2\pi r$. Se nos da información sobre cómo la duración de$r$ los cambios con respecto al tiempo; es decir, se nos dice$\frac{dr}{dt} = 5$ en/hr. Queremos saber cómo cambia la duración de$C$ los cambios con respecto al tiempo, es decir, queremos saber$\frac{dC}{dt}$.

Diferenciar implícitamente ambos lados de$C = 2\pi r$ con respecto a$t$:

\ [\ begin {align*} C &= 2\ pi r\\ frac {d} {dt}\ grande (C\ grande) &=\ frac {d} {dt} {dt}\ grande (2\ pi r\ grande)\\ frac {dC} {dt} &= 2\ pi\ frac {dr} {dt}.
\ end {alinear*}\]

Como sabemos$\frac{dr}{dt} = 5$ en/hr, sabemos

$$\ frac {dC} {dt} = 2\ pi 5 = 10\ pi\ aprox 31.4\ texto {in/hr.}\]

Considera otro ejemplo similar.

Ejemplo$\PageIndex{2}$: Finding related rates

El agua sale de un grifo a una velocidad de$2$$^3$ pulgadas/s sobre una superficie plana a una velocidad constante, formando un charco circular que está$1/8$ en profundidad.

¿A qué ritmo crece el área del charco?
¿A qué ritmo crece el radio del círculo?

Solución

1. Podemos responder a esta pregunta de dos maneras: usando “sentido común” o tasas relacionadas. El método del sentido común establece que el volumen del charco está creciendo$2$ en$^3$ /s, donde

\[\text{volume of puddle}\, =\, \text{area of circle} \times \text{depth}.\]

Dado que la profundidad es constante en$1/8$ in, el área debe estar creciendo en 16$^2$ pulgadas/s.

Este enfoque revela el principio subyacente de las tasas relacionadas. Dejar$V$ y$A$ representar el Volumen y Área del charco. Lo sabemos$V= A\times \frac18$. Tomar la derivada de ambos lados con respecto a$t$, empleando diferenciación implícita.

\[\begin{align} V &= \frac18A\\ \frac{d}{dt}\big(V\big) &= \frac{d}{dt}\left(\frac18A\right)\\ \frac{dV}{dt} &= \frac18\frac{dA}{dt} \end{align}\]

Como$\frac{dV}{dt} = 2$, sabemos$2 = \frac18\frac{dA}{dt}$, y por lo tanto$\frac{dA}{dt} = 16$. Así el área está creciendo en 16in$^2$ /s.

2. Para comenzar, necesitamos una ecuación que relacione lo que conocemos con el radio. Acabamos de aprender algo sobre la superficie del charco circular, y lo sabemos$A = \pi r^2$. Deberíamos ser capaces de conocer la velocidad a la que crece el radio con esta información.

Derivar implícitamente ambos lados de$A=\pi r^2$ con respecto a$t$:

\[\begin{align} A &= \pi r^2 \\ \frac{d}{dt}\big(A\big) &= \frac{d}{dt}\big(\pi r^2\big)\\ \frac{dA}{dt} &= 2\pi r\frac{dr}{dt} \end{align}\]

Nuestro trabajo anterior nos dijo que$\frac{dA}{dt} = 16\text{in}^2$ /s. Resolviendo para$\frac{dr}{dt}$, tenemos

$$\ frac {dr} {dt} =\ frac {8} {\ pi r}.\]

Observe cómo nuestra respuesta no es un número, sino más bien una función de$r$. En otras palabras, la velocidad a la que está creciendo el radio depende de cuán grande sea ya el círculo. Si el círculo es muy grande, agregar 2in$^3$ de agua no hará que el círculo sea mucho más grande en absoluto. Si el círculo mide el tamaño de un dímetro, agregar la misma cantidad de agua hará un cambio radical en el radio del círculo.

De alguna manera, nuestro problema estaba (intencionalmente) mal planteado. Necesitamos especificar un radio de corriente para conocer una tasa de cambio. Cuando el charco tiene un radio de 10in, el radio está creciendo a una velocidad de

$$\ frac {dr} {dt} =\ frac {8} {10\ pi} =\ frac {4} {5\ pi}\ approx 0.25\ texto {in/s}.\]

Ejemplo$\PageIndex{3}$: Studying related rates

Las pistolas de radar miden la tasa de cambio de distancia entre la pistola y el objeto que está midiendo. Por ejemplo, una lectura de “55 mph” significa que el objeto se aleja de la pistola a una velocidad de 55 millas por hora, mientras que una medición de "$-25$mph” significaría que el objeto se acerca a la pistola a una velocidad de 25 millas por hora.

Si la pistola radar se mueve (digamos, adherida a un carro de policía) entonces las lecturas del radar solo son comprensibles de inmediato si la pistola y el objeto se mueven a lo largo de la misma línea. Si un oficial de policía viaja 60 mph y obtiene una lectura de 15 mph, sabe que el automóvil que tiene delante se aleja a razón de 15 millas por hora, lo que significa que el automóvil viaja 75 mph. (Este principio de línea recta es una de las razones por las que los oficiales se estacionan al costado de la carretera e intentan disparar hacia atrás por la carretera. Da la lectura más precisa.)

Supongamos que un oficial está conduciendo hacia el norte a 30 mph y ve un automóvil moviéndose hacia el este, como se muestra en la Figura$\PageIndex{1}$. Usando su pistola radar, mide una lectura de 20mph. Al usar puntos de referencia, cree que tanto él como el otro automóvil están a aproximadamente 1/2 milla de la intersección de sus dos caminos.

$alt$

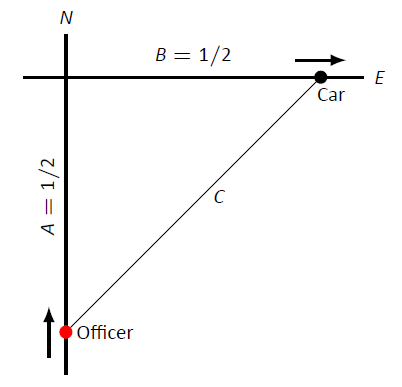
Figura$\PageIndex{1}$: Un boceto de un carro de policía (en la parte inferior) intentando medir la velocidad de un automóvil (a la derecha) en Ejemplo$\PageIndex{3}$.

Si el límite de velocidad en la otra carretera es de 55mph, ¿el otro conductor va a exceso de velocidad?

Solución

Usando el diagrama de la Figura$\PageIndex{1}$, etiquetemos lo que sabemos sobre la situación. Como tanto el oficial de policía como otro conductor están a 1/2 milla de la intersección, tenemos$A = 1/2$,$B = 1/2$, y a través del Teorema de Pitágoras,$C = 1/\sqrt{2}\approx 0.707$.

Sabemos que el policía viaja a 30 mph; es decir,$\frac{dA}{dt} = -30$. La razón por la que esta tasa de cambio es negativa$A$ es que se está haciendo más pequeña; la distancia entre el oficial y la intersección se está reduciendo. La medición del radar es$\frac{dC}{dt} = 20$. Queremos encontrar$\frac{dB}{dt}$.

Necesitamos una ecuación que se$B$ relacione con$A$ y/o$C$. El Teorema de Pitágoras es una buena opción:$A^2+B^2 = C^2$. Diferenciar ambos lados con respecto a$t$:

\[\begin{align} A^2 + B^2 &= C^2 \\ \frac{d}{dt}\left(A^2+B^2\right) &= \frac{d}{dt}\left(C^2\right) \\ 2A\frac{dA}{dt} + 2B\frac{dB}{dt} &= 2C\frac{dC}{dt} \end{align} \]

Tenemos valores para todo excepto$\frac{dB}{dt}$. Resolviendo para esto tenemos

$$\ frac {dB} {dt} =\ frac {C\ frac {dC} {dt} - A\ frac {dA} {dt}} {dt}} {B}\ aprox 58.28\ texto {mph}.\]

El otro conductor parece estar a exceso de velocidad ligeramente.

Nota:$\PageIndex{3}$ El ejemplo es interesante y poco práctico. Destaca la dificultad de usar el radar de manera no lineal, y explica por qué “en la vida real” el policía seguiría al otro conductor para determinar su velocidad, y no sacaría lápiz y papel.

Sin embargo, los principios aquí son importantes. Muchos vehículos automatizados hacen juicios sobre otros objetos en movimiento basados en distancias percibidas, mediciones similares a radares y los conceptos de tarifas relacionadas.

Ejemplo$\PageIndex{4}$: Studying related rates

Se coloca una cámara en un trípode a 10 pies del costado de una carretera. La cámara es para dar la vuelta para rastrear un automóvil que va a pasar a 100 mph para un video promocional. Los planificadores del video quieren saber con qué tipo de motor debe estar equipado el trípode para poder rastrear correctamente el automóvil a medida que pasa. En la figura se$\PageIndex{2}$ muestra la configuración propuesta.

$alt$

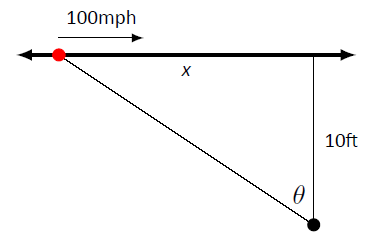
Figura$\PageIndex{2}$: Seguimiento de un automóvil a exceso de velocidad (a la izquierda) con una cámara giratoria.

¿Qué tan rápido debe poder girar la cámara para rastrear el automóvil?

Solución

Buscamos información sobre qué tan rápido es la cámara para girar; por lo tanto, necesitamos una ecuación que relacione un ángulo$\theta$ con la posición de la cámara y la velocidad y posición del automóvil.

La figura$\PageIndex{2}$ sugiere que utilizamos una ecuación trigonométrica. Dejando$x$ representar la distancia que se encuentra el carro desde el punto en la carretera directamente frente a la cámara, tenemos

\[ \tan \theta = \frac{x}{10}\]

Como el auto se mueve a 100mph, tenemos$\frac{dx}{dt} = -100$ mph (como en el último ejemplo, ya que$x$ es cada vez más pequeño a medida que el auto viaja,$\frac{dx}{dt}$ es negativo). Necesitamos convertir las medidas para que usen las mismas unidades; reescribir -100mph en cuanto a ft/s:

$$\ frac {dx} {dt} = -100\ frac {\ text {m}} {\ text {hr}} = -100\ frac {\ text {m}} {\ text {hr}}\ cdot5280\ frac {\ texto {ft}} {\ texto {m}}\ cdot\ frac {1} {3600}\ frac {\ texto {hr} {\ text {s}} =-146. \ overline {6}\ texto {ft/s}.\]

Ahora toma la derivada de ambos lados de la ecuación$\PageIndex{9}$ usando diferenciación implícita:

\[\begin{align} \tan \theta &= \frac{x}{10} \\ \frac{d}{dt}\big(\tan \theta\big) &= \frac{d}{dt}\left(\frac{x}{10}\right) \\ \sec^2\theta\,\frac{d\theta}{dt} &= \frac{1}{10}\frac{dx}{dt}\\ \frac{d\theta}{dt} &= \frac{\cos^2\theta}{10}\frac{dx}{dt} \end{align}\]

Queremos saber lo más rápido que tiene que girar la cámara. El sentido común nos dice que esto es cuando el auto está directamente frente a la cámara (es decir, cuándo$\theta = 0$). Nuestras matemáticas lo avalan. En Ecuación$\PageIndex{14}$ vemos que esto es cuando$\cos^2\theta$ es mayor; esto es cuándo$\cos \theta = 1$, o cuándo$\theta = 0$.

Con$\frac{dx}{dt} \approx -146.67$ pies/s, tenemos

$$\ frac {d\ theta} {dt} = -\ frac {1\ text {rad}} {10\ text {ft}} 146.67\ text {ft/s} = -14.667\ text {radians/s}.\]

Encontramos que$\frac{d\theta}{dt}$ es negativo; esto coincide con nuestro diagrama en Figura$\PageIndex{2}$ porque$\theta$ es cada vez más pequeño a medida que el automóvil se acerca a la cámara.

¿Cuál es el significado práctico de$-14.667$ radianes/s? Recordemos que 1 revolución circular pasa por$2\pi$ radianes, así$14.667$ rad/s significa$14.667/(2\pi)\approx 2.33$ revoluciones por segundo. El signo negativo indica que la cámara está girando en sentido horario.

Introducimos la derivada como una función que da las pendientes de líneas tangentes de funciones. Este capítulo enfatiza el uso de la derivada de otras maneras. El Método de Newton utiliza la derivada para aproximar raíces de funciones; esta sección enfatiza el aspecto de “tasa de cambio” de la derivada para encontrar una relación entre las tasas de cambio de dos cantidades relacionadas. En la siguiente sección utilizamos conceptos de Valor Extremo para optimizar cantidades.