4.4: Diferenciales

En la Sección 2.2 exploramos el significado y uso de la derivada. Esta sección comienza revisitando algunas de esas ideas.

Recordemos que la derivada de una función$f$ puede ser utilizada para encontrar las pendientes de líneas tangentes a la gráfica de$f$. At$x=c$, la línea tangente a la gráfica de$f$ tiene ecuación

$$y = f' (c) (x-c) +f (c).\]

La línea tangente se puede utilizar para encontrar buenas aproximaciones de$f(x)$ para valores de$x$ cerca$c$.

Por ejemplo, podemos aproximarnos$\sin 1.1$ usando la línea tangente a la gráfica de$f(x)=\sin x$ en$x=\pi/3 \approx 1.05.$ Recall that$\sin (\pi/3) = \sqrt{3}/2 \approx 0.866$, y$\cos (\pi/3) = 1/2$. Así, la línea tangente a$f(x) = \sin x$ at$x=\pi/3$ es:

$$\ ell (x) =\ frac12 (x-\ pi/3) +0.866.\]

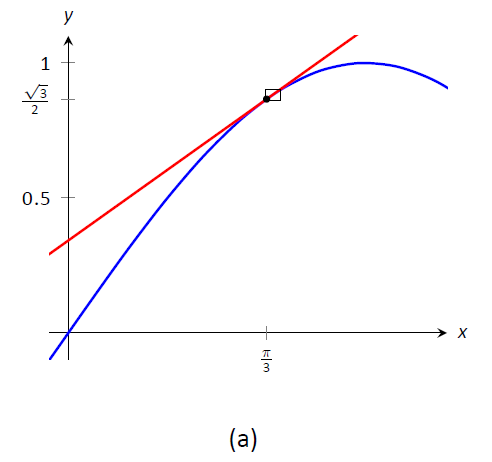
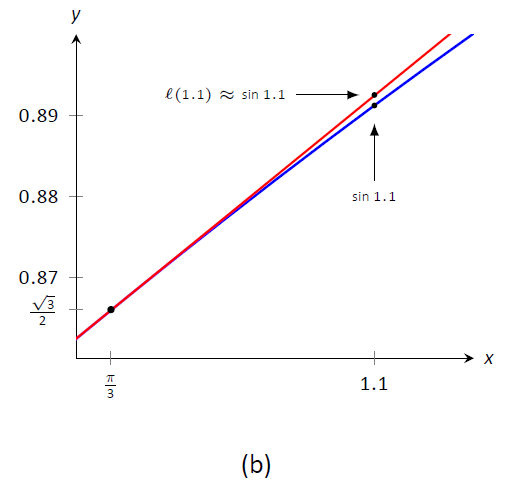
Figura$\PageIndex{1}$: Gráfica$f(x) = \sin x$ y su línea tangente$x=\pi/3$ en para estimar$\sin 1.1$.

En la Figura$\PageIndex{1a}$, vemos un gráfico de$f(x) = \sin x$ graficado junto con su línea tangente en$x=\pi/3$. El rectángulo pequeño muestra la región que se muestra en la Figura$\PageIndex{1b}$. En esta figura, vemos cómo nos estamos aproximando$\sin 1.1$ con la línea tangente, evaluada en$1.1$. En conjunto, las dos cifras muestran lo cerca que están estos valores.

Usando esta línea para aproximar$\sin 1.1$, tenemos:

$$\begin{align} \ell(1.1) &= \frac12(1.1-\pi/3)+0.866 \\ &= \frac12(0.053)+0.866 = 0.8925. \end{align}$$

(Dejamos al lector ver qué tan buena aproximación es esta.)

Ahora generalizamos este concepto. Dado$f(x)$ y un$x$ valor —valor$c$, la línea tangente es$\ell(x) = f'(c)(x-c)+f(c)$. Claramente,$f(c) = \ell(c)$. Dejar$\Delta x$ ser un número pequeño, que representa un pequeño cambio en el$x$ valor. Aafirmamos que:

$$f (c+\ Delta x)\ aprox\ ell (c+\ Delta x),\]

ya que la línea tangente a una función se aproxima bien a los valores de esa función cerca$x=c$.

A medida que el$x$ valor cambia de$c$ a$c+\Delta x$, el$y$ valor de$f$ los cambios de$f(c)$ a$f(c+\Delta x)$. A esto lo llamamos cambio de$y$ valor$\Delta y$. Es decir:

$$\ Delta y = f (c+\ Delta x) -f (c).\]

Sustituyendo$f(c+\Delta x)$ con su aproximación de línea tangente, tenemos

$$\begin{align} \Delta y &\approx \ell(c+\Delta x) - f(c) \notag\\ &= f'(c)\big((c+\Delta x)-c\big)+f(c) - f(c)\notag \\ &=f'(c)\Delta x \end{align}$$

Esta ecuación final es importante; volveremos a ella en la Idea Clave 7.

Introducimos dos nuevas variables,$dx$ y$dy$ en el contexto de una definición formal.

Definición: Diferenciales de$x$ and $y$.

Que$y=f(x)$ sean diferenciables. El diferencial de$x$, denotado$dx$, es cualquier número real distinto de cero (generalmente tomado como un número pequeño). El diferencial de$y$, denotado$dy$, es

$$dy = f'(x)dx.$$

Podemos resolver para$f'(x)$ en la ecuación anterior:$f'(x) = dy/dx$. Esto establece que la derivada de$f$ con respecto a$x$ es el diferencial de$y$ dividido por el diferencial de$x$; esta no es la notación alternativa para la derivada,$\frac{dy}{dx}$. Esta última notación se eligió por las cualidades fraccionadas de la derivada, pero nuevamente, es un símbolo y no una fracción.

Es útil organizar nuestros nuevos conceptos y notaciones en un solo lugar.

Idea Clave 7: Notación Diferencial

Dejar$y = f(x)$ ser una función diferenciable.

1. $\Delta x$representa un pequeño cambio distinto de cero en el$x$ valor.
2. $dx$representa un pequeño cambio distinto de cero en el$x$ valor (es decir,$\Delta x = dx$).
3. $\Delta y$es el cambio de$y$ valor como$x$ cambios por$\Delta x$; de ahí $$\ Delta y = f (x+\ Delta x) -f (x) .$$
4. $dy = f'(x)dx$que, por Ecuación$\PageIndex{7}$, es una aproximación del cambio de$y$ valor como$x$ cambios por$\Delta x$;$dy \approx \Delta y$.

¿Cuál es el valor de los diferenciales? Al igual que muchos conceptos matemáticos, los diferenciales proporcionan beneficios tanto prácticos como teóricos. Exploramos ambos aquí.

Ejemplo$\PageIndex{1}$: Finding and using differentials

Considerar$f(x) = x^2$. Conociendo$f(3) = 9$, aproximado$f(3.1)$.

Solución

El$x$ valor va cambiando de$x=3$ a$x=3.1$; por lo tanto, eso lo vemos$dx=0.1$. Si sabemos cuánto cambia el$y$ valor de$f(3)$ a$f(3.1)$ (es decir, si sabemos$\Delta y$), sabremos exactamente qué$f(3.1)$ es (ya lo sabemos$f(3)$). Podemos aproximar\ Delta y\ con$dy$.

$$\begin{align} \Delta y &\approx dy \\ &= f'(3)dx \\ &= 2\cdot 3\cdot 0.1 = 0.6. \end{align}$$

Esperamos que el$y$ valor cambie aproximadamente$0.6$, así que aproximamos$f(3.1) \approx 9.6.$

Dejamos al lector verificar esto, pero la discusión anterior vincula el diferencial a la línea tangente de$f(x)$ at$x=3$. Se puede verificar que la línea tangente, evaluada en$x=3.1$, también da$y=9.6$.

Por supuesto, es fácil calcular la respuesta real (a mano o con una calculadora):$3.1^2 = 9.61.$ (Antes de ponernos demasiado cínicos y decir “Entonces, ¿por qué molestarnos?” , tenga en cuenta que nuestra aproximación es realmente buena!)

Entonces ¿por qué molestarse?

En “la mayoría” de las situaciones de la vida real, desconocemos la función que describe un comportamiento particular. En cambio, solo podemos tomar medidas de cómo cambian las cosas — mediciones de la derivada.

Imagina que el agua fluye por un canal sinuoso. Es fácil medir la velocidad y dirección (es decir, la velocidad) del agua en cualquier lugar. Es muy difícil crear una función que describa el flujo general, de ahí que sea difícil predecir dónde terminará un objeto flotante colocado al comienzo del canal. Sin embargo, podemos aproximar la ruta de un objeto usando diferenciales. A intervalos pequeños, la trayectoria tomada por un objeto flotante es esencialmente lineal. Los diferenciales nos permiten aproximar el camino verdadero al juntar lotes de caminos cortos y lineales. Esta técnica se llama Método de Euler, estudiada en cursos introductorios de Ecuaciones Diferenciales.

Utilizamos diferenciales una vez más para aproximar el valor de una función. A pesar de que las calculadoras son muy accesibles, es genial ver cómo estas técnicas a veces se pueden usar para calcular fácilmente algo que parece bastante duro.

Ejemplo$\PageIndex{2}$: Using differentials to approximate a function value

Aproximado$\sqrt{4.5}$.

Solución

Esperamos$\sqrt{4.5} \approx 2$, sin embargo podemos hacerlo mejor. Vamos$f(x) = \sqrt{x}$, y vamos$c=4$. Así$f(4) = 2$. Podemos calcular$f'(x) = 1/(2\sqrt{x})$, entonces$f'(4) = 1/4$.

Aproximamos la diferencia entre$f(4.5)$ y$f(4)$ usando diferenciales, con$dx = 0.5$:

$$f (4.5) -f (4) =\ Delta y\ approx dy = f' (4)\ cdot dx = 1/4\ cdot 1/2 = 1/8 = 0.125.\]

El cambio aproximado en$f$ de$x=4$ a$x=4.5$ es$0.125$, por lo que aproximamos$\sqrt{4.5} \approx 2.125.$

Los diferenciales son importantes cuando hablamos de integración. Cuando estudiemos ese tema, usaremos notación como

$$\ int f (x)\ dx\]

muy a menudo. Si bien no discutimos aquí qué significa toda esa notación, nótese la existencia del diferencial$dx$. El manejo adecuado de las integrales viene con el manejo adecuado de los diferenciales.

A la luz de eso, practicamos encontrar diferenciales en general.

Ejemplo$\PageIndex{3}$: Finding differentials

En cada una de las siguientes, encuentra el diferencial$dy$.

$$y = \sin x \qquad\quad 2. y = e^x(x^2+2) \quad\qquad 3. y = \sqrt{x^2+3x-1}$$

S olución

1. $y = \sin x$: Como$f(x) = \sin x$,$f'(x) = \cos x$. Así $$dy =\ cos (x) dx.$$
2. $y = e^x(x^2+2)$: Vamos$f(x) = e^x(x^2+2)$. Necesitamos$f'(x)$, requiriendo la Regla del Producto.
   Tenemos$f'(x) = e^x(x^2+2) + 2xe^x$, así que $$dy =\ big (e^x (x^2+2) + 2xe^x\ big) dx.$$
3. $y = \sqrt{x^2+3x-1}$: Vamos$f(x) = \sqrt{x^2+3x-1}$; necesitamos$f'(x)$, requiriendo la Regla de la Cadena.
   Tenemos$\Delta s f'(x) = \frac{1}{2}(x^2+3x-1)^{-\frac12}(2x+3) = \frac{2x+3}{2\sqrt{x^2+3x-1}}.$ Así $$dy =\ frac {(2x+3) dx} {2\ sqrt {x^2+3x-1}} .$$

Encontrar el diferencial$dy$ de no$y=f(x)$ es realmente más difícil que encontrar la derivada de$f$; simplemente multiplicamos$f'(x)$ por$dx$. Es importante recordar que no estamos simplemente agregando el símbolo "$dx$" al final.

Hemos visto un uso práctico de los diferenciales ya que ofrecen un buen método para hacer ciertas aproximaciones. Otro uso es la propagación de errores. Supongamos que se mide una longitud para ser$x$, aunque el valor real es$x+\Delta x$ (donde esperamos\ Delta x\ sea pequeño). Esta medición de$x$ puede ser utilizada para calcular algún otro valor; podemos pensar en esto como$f(x)$ para alguna función$f$. Como es la longitud verdadera$x+\Delta x$, uno realmente debería haber calculado$f(x+\Delta x)$. La diferencia entre$f(x)$ y$f(x+\Delta x)$ es el error propagado.

¿Qué tan cerca están$f(x)$ y$f(x+\Delta x)$? Esta es una diferencia en los valores “y”;

$$f (x+\ Delta x) -f (x) =\ Delta y\ día aprox.\]

Podemos aproximar el error propagado usando diferenciales.

Ejemplo$\PageIndex{4}$: Using differentials to approximate propagated error

Un rodamiento de bolas de acero debe fabricarse con un diámetro de 2cm. El proceso de fabricación tiene una tolerancia de$\pm 0.1$ mm en el diámetro. Dado que la densidad del acero es de aproximadamente 7.85g/cm$^3$, estime el error propagado en la masa del rodamiento de bolas.

Solución

La masa de un rodamiento de bolas se encuentra usando la ecuación “masa =$\times$ densidad volumétrica”. En esta situación la función de masa es producto del radio del rodamiento de bolas, de ahí que lo sea$m = 7.85\frac43\pi r^3$. El diferencial de la masa es

$$dm = 31.4\ pi r^2 dr.\]

El radio debe ser de 1cm; la tolerancia de fabricación en el radio es$\pm 0.05$ mm, o$\pm 0.005$ cm. El error propagado es aproximadamente:

$$\begin{align} \Delta m & \approx dm \\ &= 31.4\pi (1)^2 (\pm 0.005) \\ &= \pm 0.493\text{g} \end{align}$$

¿Este error es significativo? Ciertamente depende de la aplicación, pero podemos hacernos una idea calculando el error relativo. La relación entre la cantidad de error y la masa total es

$$\begin{align} \frac{dm}{m} &= \pm \frac{0.493}{7.85\frac43\pi} \\ &=\pm \frac{0.493}{32.88}\\ &=\pm 0.015,\end{align}$$

o$\pm 1.5$.

Dejamos al lector confirmar esto, pero si se suponía que el diámetro de la bola era de 10cm, la misma tolerancia de fabricación daría un error propagado en masa de$\pm12.33$ g, que corresponde a un\ textit {error porcentual} de$\pm0.188$\%. Si bien la cantidad de error es mucho mayor ($12.33 > 0.493$), el porcentaje de error es mucho menor.

Primero aprendimos de la derivada en el contexto de tasas de cambio instantáneas y pendientes de líneas tangentes. Ampliamos nuestra comprensión del poder de la derivada al estudiar cómo se relaciona con la gráfica de una función (conduciendo a ideas de aumento/decreciente y concavidad). Este capítulo ha puesto la derivada a aún más usos:

• Resolución de ecuaciones (Método de Newton)
• Tarifas relacionadas (fomentando nuestro uso de la derivada para encontrar tasas de cambio instantáneas)
• Optimización (valores extremos aplicados), y
• Diferenciales (útiles para diversas aproximaciones y para algo llamado integración).

En los capítulos siguientes, consideraremos el problema “inverso” para computar la derivada: dada una función$f$, ¿podemos encontrar una función cuya derivada es$f$? Poder hacerlo abre un increíble mundo de matemáticas y aplicaciones.

Colaboradores y Atribuciones

• Template:ContribApexCalc
• Template:ContribMarshall