7.1: Área entre curvas

Última actualización
Guardar como PDF

Page ID: 111787

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos este capítulo con un recordatorio de algunos conceptos clave del Capítulo 5. Dejar$f$ ser una función continua en la$[a,b]$ que se divide en$n$ subintervalos como

$$a<x_1 < x_2 <\ cdots < x_n<x_ {n+1} =b.\]

Dejar$dx_i$ denotar la longitud del$i^\text{ th}$ subintervalo, y dejar que$c_i$ sea cualquier$x$ -valor en ese subintervalo. La definición 5.3.1 establece que la suma

$$\ suma_ {i=1} ^n f (c_i)\ dx_i\]

es una suma de Riemann. Riemann Las sumas suelen utilizarse para aproximar alguna cantidad (área, volumen, trabajo, presión, etc.). La aproximación se vuelve exacta tomando el límite

$$\ lim_ {||dx_i||\ to0}\ suma_ {i=1} ^n f (c_i)\ dx_i,\]

donde$||\ dx_i||$ la longitud del subintervalo más grande en la partición. Teorema 5.3.2 conecta los límites de las sumas de Riemann a integrales definidas:

$$\ lim_ {||dx_i||\ to0}\ suma_ {i=1} ^n f (c_i)\ dx_i =\ int_a^b f (x)\ dx.\]

Finalmente, el Teorema Fundamental del Cálculo establece cómo las integrales definidas pueden ser evaluadas usando antiderivados.

Este capítulo emplea la siguiente técnica para una variedad de aplicaciones. Supongamos que se va a calcular el valor$Q$ de una cantidad. Primero aproximamos el valor de$Q$ usar una suma de Riemann, luego encontramos el valor exacto a través de una integral definida. Deletreamos esta técnica en la siguiente Idea Clave.

Idea Clave 22: Estrategia Integral Definida

Dejar que se dé una cantidad cuyo valor$Q$ se va a calcular.

Divida la cantidad en “subcantidades”$n$ más pequeñas de valor$Q_i$.
Identificar una variable$x$ y función$f(x)$ tal que cada subcantidad pueda aproximarse con el producto$f(c_i)\ dx_i$, donde$dx_i$ representa un pequeño cambio en$x$. Por lo tanto$Q_i \approx f(c_i)\ dx_i$. Una aproximación$f(c_i)\ dx_i$ de muestra de$Q_i$ se llama elemento diferencial.
Reconocer eso$ Q= \sum_{i=1}^n Q_i \approx \sum_{i=1}^n f(c_i)\ dx_i$, que es un Riemann Sum.
Tomando el límite apropiado da$ Q = \int_a^b f(x)\ dx$

Esta Idea Clave tendrá más sentido después de que hayamos tenido la oportunidad de usarla varias veces. Comenzamos con Área Entre Curvas, que abordamos brevemente en la Sección 5.5.4.

Área entre curvas

A menudo nos interesa conocer el área de una región. Olvida momentáneamente que ya abordamos esto en la Sección 5.5.4 y abordarlo en su lugar utilizando la técnica descrita en la Idea Clave 22.

Dejar$Q$ ser el área de una región delimitada por funciones continuas$f$ y$g$. Si dividimos la región en muchas subregiones, tenemos una ecuación obvia:

\[\text{Total Area} = \text{sum of the areas of the subregions.}\]

El tema a abordar a continuación es cómo dividir sistemáticamente una región en subregiones. Una gráfica ayudará. Considere Figura$\PageIndex{1a}$ donde se sombrea una región entre dos curvas. Si bien hay muchas formas de dividirlo en subregiones, una forma particularmente eficiente es “cortarlo” verticalmente, como se muestra en la Figura$\PageIndex{1b}$, en rebanadas$n$ igualmente espaciadas.

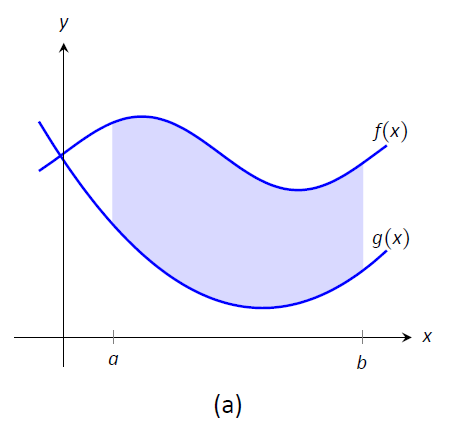
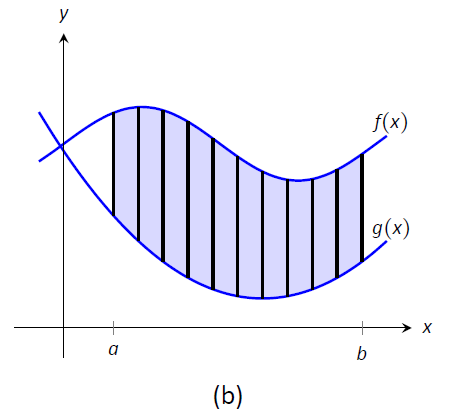
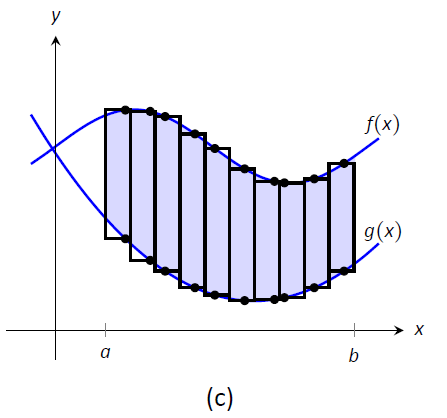
$7.1.1a.png$ $7.1.1b.png$ $7.1.1c.png$

Figura$\PageIndex{1}$: Subdividir una región en cortes verticales y aproximar las áreas con rectángulos.

Ahora aproximamos el área de una rebanada. Nuevamente, tenemos muchas opciones, pero usar un rectángulo parece más sencillo. Escogiendo cualquier$x$ -valor$c_i$ en la$i^\text{ th}$ rebanada, establecemos la altura del rectángulo para que sea$f(c_i)-g(c_i)$, la diferencia de los$y$ valores -correspondientes. El ancho del rectángulo es una pequeña diferencia en$x$ -valores, que representamos con$dx$. La figura$\PageIndex{1c}$ muestra los puntos de muestra$c_i$ elegidos en cada subintervalo y los rectángulos apropiados dibujados. (Cada uno de estos rectángulos representa un elemento diferencial). Cada porción tiene un área aproximadamente igual a$\big(f(c_i)-g(c_i)\big)\ dx$; por lo tanto, el área total es aproximadamente la suma de Riemann

$$Q =\ suma_ {i=1} ^n\ grande (f (c_i) -g (c_i)\ grande)\ dx.\]

Tomando el límite como$n\to \infty$ da el área exacta como$\int_a^b \big(f(x)-g(x)\big)\ dx.$

Thermoem$\PageIndex{1}$: Area Between Curves

Dejar$f(x)$ y$g(x)$ ser funciones continuas definidas sobre$[a,b]$ dónde$f(x)\geq g(x)$ para todos$x$ en$[a,b]$. El área de la región delimitada por las curvas$y=f(x)$,$y=g(x)$ y las líneas$x=a$ y$x=b$ es

$$\ int_a^b\ grande (f (x) -g (x)\ grande)\ dx.\]

Ejemplo$\PageIndex{1}$: Finding area enclosed by curves

Encuentra el área de la región delimitada por$f(x) = \sin x+2$,,$x=0$ y$g(x) = \dfrac12\cos (2x)-1$$x=4\pi$, como se muestra en la Figura$\PageIndex{2}$.

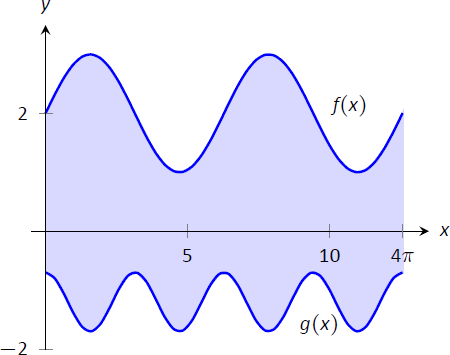
$imageedit_2_9982172939.png$

Figura$\PageIndex{2}$: Graficando una región cerrada en Ejemplo$\PageIndex{1}$.

Solución

La gráfica verifica que el límite superior de la región está dado por$f$ y el límite inferior está dado por$g$. Por lo tanto, el área de la región es el valor de la integral

\[\begin{align*}\int_0^{4\pi} \big(f(x)- g(x)\big)\ dx & = \int_0^{4\pi} \Big(\sin x+2 - \big(\dfrac12\cos (2x)-1\big)\Big)\ dx \\[4pt]&= -\cos x -\dfrac14\sin(2x)+3x\Big|_0^{4\pi}\\[4pt] &= 12\pi \approx 37.7\ \text{units}^2.\end{align*}\]

Ejemplo$\PageIndex{2}$: Finding total area enclosed by curves

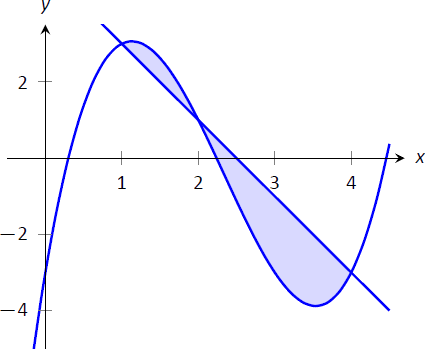
Encuentra el área total de la región encerrada por las funciones$f(x) = -2x+5$ y$g(x) = x^3-7x^2+12x-3$ como se muestra en la Figura$\PageIndex{3}$.

$imageedit_6_8824349634.png$

Figura$\PageIndex{3}$: Graficando una región encerrada por dos funciones en Ejemplo$\PageIndex{2}$.

Solución

Un cálculo rápido muestra que$f=g$ en$x=1, 2$ y 4. Se puede proceder sin pensar por la computación$ \int_1^4\big(f(x)-g(x)\big)\ dx$, pero esto ignora el hecho de que en$[1,2]$,$g(x)>f(x)$. (De hecho, la integración irreflexiva regresa$-9/4$, apenas el valor esperado de una zona.) Así, calculamos el área total dividiendo el intervalo$[1,4]$ en dos subintervalos,$[1,2]$$[2,4]$ y usando el integrando adecuado en cada uno.

\[\begin{align*} \text{Total Area} &= \int_1^2 \big(g(x)-f(x)\big)\ dx + \int_2^4\big(f(x)-g(x)\big)\ dx\\[4pt] &= \int_1^2 \big(x^3-7x^2+14x-8\big) \ dx + \int_2^4\big(-x^3+7x^2-14x+8\big)\ dx\\[4pt] &= 5/12 + 8/3 \\[4pt] &= 37/12 = 3.083\ \text{units}^2.\end{align*} \]

El ejemplo anterior hace notar que estamos esperando que el área sea positiva. Al aprender por primera vez sobre la integral definida, la interpretamos como “área firmada bajo la curva”, permitiendo “área negativa”. Eso no aplica aquí; área es ser positivo.

El ejemplo anterior también demuestra que muchas veces tenemos que dividir una región dada en subregiones antes de aplicar el Teorema$\PageIndex{1}$. El siguiente ejemplo muestra otra situación en la que esto es aplicable, junto con una visión alternativa de aplicar el Teorema.

Ejemplo$\PageIndex{3}$: Finding area: integrating with respect to $y$

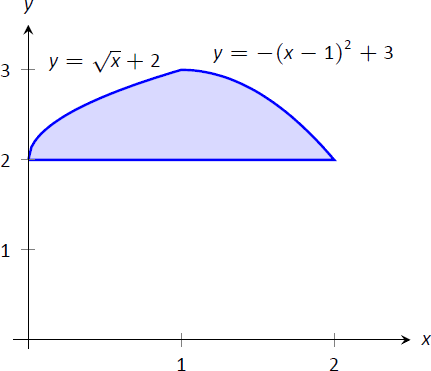
Encuentra el área de la región encerrada por las funciones$y=\sqrt{x}+2$,$y=-(x-1)^2+3$ y$y=2$, como se muestra en la Figura$\PageIndex{4}$.

$imageedit_10_2062732782.png$

Figura$\PageIndex{4}$: Graficando una región para Ejemplo$\PageIndex{3}$.

Solución

Damos dos enfoques a este problema. En el primer enfoque, notamos que el “top” de la región está definido por dos curvas diferentes. On$[0,1]$, la función superior es$y=\sqrt{x}+2$; on$[1,2]$, la función superior es$y=-(x-1)^2+3$.

Así calculamos el área como la suma de dos integrales:

\[\begin{align*} \text{Total Area} &= \int_0^1 \Big(\big(\sqrt{x}+2\big)-2\Big)\ dx + \int_1^2 \Big(\big(-(x-1)^2+3\big)-2\Big)\ dx \\[4pt] &= 2/3 + 2/3\\[4pt] &=4/3.\end{align*}\]

El segundo enfoque es inteligente y muy útil en ciertas situaciones. Estamos acostumbrados a ver las curvas como funciones de$x$; ingresamos un$x$ -value y se devuelve un$y$ -value. Algunas curvas también pueden describirse como funciones de$y$: entrada a$y$ -value y se devuelve un$x$ -value. Podemos reescribir las ecuaciones que describen el límite resolviendo para$x$:

$$y=\ sqrt {x} +2\ quad\ Rightarrow\ quad x= (y-2) ^2\]

$$y=- (x-1) ^2+3\ quad\ Rightarrow\ quad x=\ sqrt {3-y} +1.\]

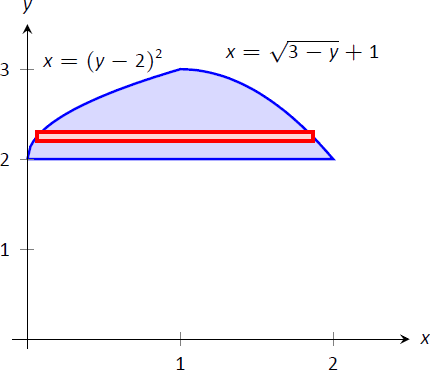
$imageedit_14_3135847777.png$

Figura$\PageIndex{5}$: La región utilizada en Ejemplo$\PageIndex{3}$ con límites reetiquetados como funciones de$y$.

La figura$\PageIndex{5}$ muestra la región con los límites reetiquetados. También se representa un elemento diferencial, un rectángulo horizontal. El ancho del rectángulo es un pequeño cambio en$y$:$\Delta y$. La altura del rectángulo es una diferencia en$x$ -valores. El valor “superior” es el$x$ valor más grande, es decir, el más a la derecha. El$x$ valor “inferior” es el más pequeño, es decir, el más a la izquierda. Por lo tanto, la altura del rectángulo es

$$\ grande (\ sqrt {3-y} +1\ grande) - (y-2) ^2.\]

El área se encuentra integrando la función anterior con respecto a$y$ los límites apropiados. Los determinamos considerando los$y$ -valores que ocupa la región. Está delimitado abajo por$y=2$, y delimitado arriba por$y=3$. Es decir, tanto las funciones “top” como “bottom” existen en el$y$ intervalo$[2,3]$. Por lo tanto

\[\begin{align*}\text{Total Area} &= \int_2^3 \big(\sqrt{3-y}+1 - (y-2)^2\big)\ dy \\[4pt] &= \Big(-\dfrac23(3-y)^{3/2}+y-\dfrac13(y-2)^3\Big)\Big|_2^3 \\[4pt] &= 4/3.\end{align*}\]

Esta técnica de búsqueda de área basada en cálculos puede ser útil incluso con formas que normalmente pensamos como “fáciles”. Ejemplo$\PageIndex{4}$ calcula el área de un triángulo. Si bien la fórmula$\dfrac12\times\text{base}\times\text{height}$ "" es bien conocida, en triángulos arbitrarios puede ser no trivial calcular la altura. El cálculo simplifica el problema.

Ejemplo$\PageIndex{4}$: Finding the area of a triangle

Calcular el área de las regiones delimitadas por las líneas

$y=x+1$,$y=-2x+7$ y$y=-\dfrac12x+\dfrac52$, como se muestra en la Figura$\PageIndex{6}$.

$imageedit_18_4655953817.png$

Figura$\PageIndex{6}$: Graficando una región triangular en el Ejemplo$\PageIndex{4}$

Solución

Reconocer que hay dos funciones “top” en esta región, lo que hace que usemos dos integrales definidas.

\[\begin{align*}\text{Total Area} &= \int_1^2\big((x+1)-(-\dfrac12x+\dfrac52)\big)\ dx + \int_2^3\big((-2x+7)-(-\dfrac12x+\dfrac52)\big)\ dx \\[4pt] &= 3/4+3/4\\[4pt] &=3/2.\end{align*}\]

También podemos abordar esto convirtiendo cada función en una función de$y$. Esto también requiere 2 integrales, por lo que realmente no hay ninguna ventaja en hacerlo. Lo hacemos aquí con fines de demostración.

La función “superior” es siempre$x=\dfrac{7-y}2$ mientras hay dos funciones “inferiores”. Siendo conscientes de los límites de integración adecuados, tenemos

\[\begin{align*} \text{Total Area} &= \int_1^2\big(\dfrac{7-y}2 - (5-2y)\big)\ dy + \int_2^3\big(\dfrac{7-y}2-(y-1)\big)\ dy \\[4pt] &= 3/4 + 3/4\\[4pt] &= 3/2.\end{align*}\]

Por supuesto, la respuesta final es la misma. (Es interesante señalar que el área de las 4 subregiones utilizadas es 3/4. Esto es una coincidencia.)

Si bien nos hemos centrado en producir respuestas exactas, también somos capaces de hacer aproximaciones utilizando el principio del Teorema$\PageIndex{1}$. El integrando en el teorema es una distancia (“arriba menos abajo”); integrando esta función distancia da un área. Al tomar medidas discretas de distancia, podemos aproximar un área utilizando técnicas de integración numérica desarrolladas en la Sección\ ref {sec:numerical_integration}. El siguiente ejemplo demuestra esto.

Ejemplo$\PageIndex{5}$: Numerically approximating area

Para aproximar el área de un lago, que se muestra en la Figura$\PageIndex{7a}$, la “longitud” del lago se mide en incrementos de 200 pies como se muestra en la Figura$\PageIndex{7b}$, donde las longitudes se dan en cientos de pies. Aproximar el área del lago.

Solución

Las medidas de longitud se pueden ver como midiendo “arriba menos abajo” de dos funciones. La respuesta exacta se encuentra integrando$\int_0^{12} \big(f(x)-g(x)\big)\ dx$, pero claro que no conocemos las funciones$f$ y$g$. Nuestras medidas discretas en cambio nos permiten aproximarnos.

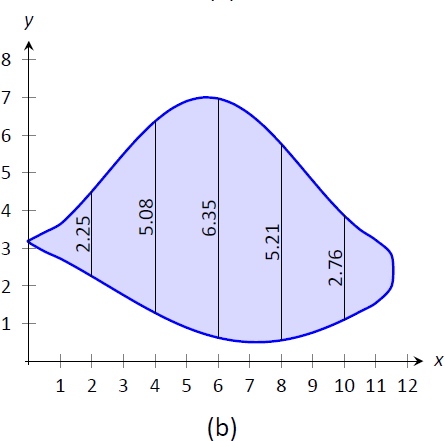
$imageedit_22_5823047485.png$ $imageedit_26_8042194042.png$

Figura$\PageIndex{7}$: (a) Un boceto de un lago, y (b) el lago con medidas de longitud.

Contamos con los siguientes puntos de datos:

$$ (0,0),\ (2,2.25),\ (4,5.08),\ (6,6.35),\ (8,5.21),\ (10,2.76),\ (12,0).\]

También tenemos eso$dx=\dfrac{b-a}{n} = 2$, así que la Regla de Simpson da

\[\begin{align*}\text{Area}&\approx \dfrac{2}{3}\Big(1\cdot0+4\cdot2.25+2\cdot5.08+4\cdot6.35+2\cdot5.21+4\cdot2.76+1\cdot0\Big)\\[4pt] &= 44.01\overline{3} \ \text{units}^2.\end{align*}\]

Ya que las medidas son en cientos de pies, unidades$^2 = (100\ \text{ft})^2 = 10,000\ \text{ft}^2$, dando un área total de$440,133\ \text{ft}^2$. (Como nos estamos aproximando, probablemente diríamos que el área estaba a punto$440,000\ \text{ft}^2$, que es un poco más de 10 acres).

En la siguiente sección aplicamos nuestras técnicas de aplicación de integración para encontrar los volúmenes de ciertos sólidos.