7.4: Longitud del arco y superficie
- Page ID
- 111791
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Longitud del arco
En secciones anteriores hemos utilizado la integración para responder a las siguientes preguntas:
- Dada una región, ¿cuál es su área?
- Dado un sólido, ¿cuál es su volumen?
En esta sección, abordamos una pregunta relacionada: Dada una curva, ¿cuál es su longitud? Esto a menudo se conoce como longitud de arco.
Considere la gráfica de\(y=\sin x\) on\([0,\pi]\) dada en la Figura\(\PageIndex{1a}\). ¿Cuánto dura esta curva? Es decir, si tuviéramos que usar un trozo de cuerda para que coincida exactamente con la forma de esta curva, ¿cuánto tiempo tendría la cuerda?
Como lo hemos hecho en el pasado, comenzamos por aproximarnos; posteriormente, refinaremos nuestra respuesta usando límites para obtener una solución exacta.
La longitud de los segmentos de línea recta es fácil de calcular con la fórmula de distancia. Podemos aproximar la longitud de la curva dada aproximando la curva con líneas rectas y midiendo sus longitudes.
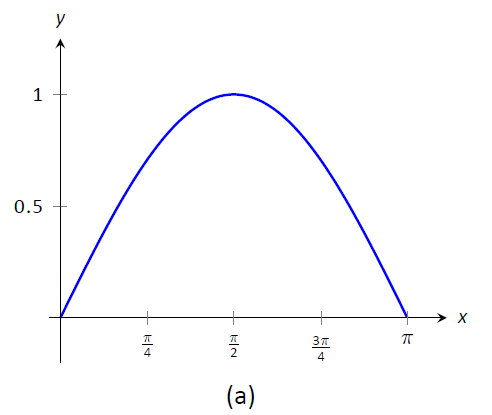
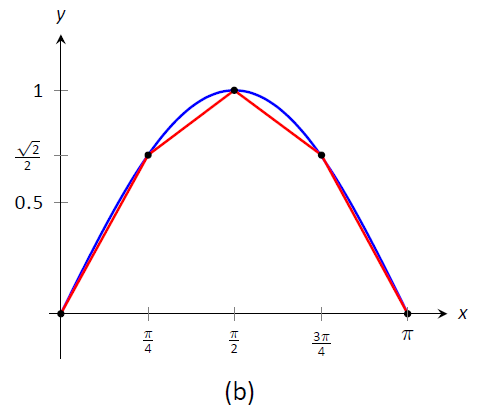
Figura\(\PageIndex{1}\): Graficar\(y=\sin x\)\([0,\pi]\) y aproximar la curva con segmentos de línea.
En la Figura\(\PageIndex{1b}\), la curva se\(y=\sin x\) ha aproximado con 4 segmentos de línea (el intervalo se\([0,\pi]\) ha dividido en 4 subintervalos de igual longitud). Es claro que estos cuatro segmentos de línea se aproximan\(y=\sin x\) muy bien en el primer y último subintervalo, aunque no tan bien en el medio. Independientemente, la suma de las longitudes de los segmentos de línea es\(3.79\), por lo que aproximamos la longitud del arco de\(y=\sin x\) on\([0,\pi]\) a ser\(3.79\).
En general, podemos aproximar la longitud del arco de\(y=f(x)\) on\([a,b]\) de la siguiente manera. Dejar\(a=x_1 < x_2 < \ldots < x_n< x_{n+1}=b\) ser una partición de\([a,b]\) en\(n\) subintervalos. Let\(dx_i\) representar la longitud del\(i\,^\text{th}\) subintervalo\([x_i,x_{i+1}]\).
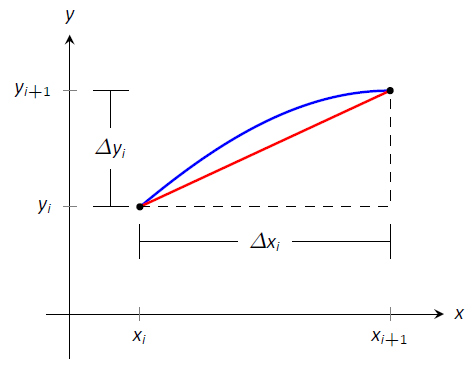
Figura\(\PageIndex{2}\): Acercar el\(i\,^\text{th}\) subintervalo\([x_i,x_{i+1}\)] de una partición de\([a,b]\).
La figura\(\PageIndex{2}\) amplía el\(i\,^\text{th}\) subintervalo donde\(y=f(x)\) se aproxima por un segmento de línea recta. Las líneas discontinuas muestran que podemos ver este segmento de línea como hipotenusa de un triángulo rectángulo cuyos lados tienen longitud\(dx_i\) y\(dy_i\). Usando el Teorema de Pitágoras, la longitud de este segmento de línea es\(\sqrt{dx_i^2 + \Delta y_i^2}.\) Sumando en todos los subintervalos da una aproximación de longitud de arco
\[L \approx \sum_{i=1}^n \sqrt{dx_i^2 + \Delta y_i^2}.\]
Como se muestra aquí, esto no es una suma de Riemann. Si bien podríamos concluir que tomar un límite ya que la longitud del subintervalo va a cero da la longitud exacta del arco, no podríamos calcular la respuesta con una integral definida. Primero tenemos que hacer un poco de álgebra.
En el factor de expresión anterior a cabo un\(dx_i^2\) término:
\[ \sum_{i=1}^n \sqrt{dx_i^2 + \Delta y_i^2} = \sum_{i=1}^n \sqrt{dx_i^2\left(1 + \frac{\Delta y_i^2}{dx_i^2}\right)}.\]
Ahora saca el\(dx_i^2\) término de la raíz cuadrada:
\[= \sum_{i=1}^n\sqrt{1 + \frac{\Delta y_i^2}{dx_i^2}}\ dx_i.\]
Esto es casi un Riemann Sum. Considera el\(\Delta y_i^2/dx_i^2\) término. La expresión\(\Delta y_i/dx_i\) mide el “cambio en\(y\) /cambio en”\(x\), es decir, el “ascenso sobre carrera” de\(f\) en el\(i\,^\text{th}\) subintervalo. El Teorema del Valor Medio de la Diferenciación (Teorema 3.2.1) establece que hay una\(c_i\) en el\(i\,^\text{th}\) subintervalo donde\(f'(c_i) = \Delta y_i/dx_i\). Así podemos reescribir nuestra expresión anterior como:
\[= \sum_{i=1}^n\sqrt{1+f'(c_i)^2}\ dx_i.\]
Se trata de un Riemann Sum. Mientras\(f'\) sea continuo, podemos invocar el Teorema 5.3.2 y concluir
\[= \int_a^b\sqrt{1+f'(x)^2}\ dx.\]
Idea Clave 27: Longitud del Arco
Dejar\(f\) ser diferenciable en un intervalo abierto que contiene\([a,b]\), donde también\(f'\) es continuo en\([a,b]\). Entonces la longitud del arco de\(f\) desde\(x=a\) a\(x=b\) es
\[L = \int_a^b \sqrt{1+f'(x)^2}\ dx.\]
Como el integrando contiene una raíz cuadrada, a menudo es difícil usar la fórmula de Key Idea 27 para encontrar exactamente la longitud. Cuando las respuestas exactas son difíciles de encontrar, recurrimos al uso de métodos numéricos para aproximar integrales definidas. Los siguientes ejemplos lo demostrarán.
Ejemplo\(\PageIndex{1}\): Finding arc length
Encuentra la longitud del arco de\(f(x) = x^{3/2}\) desde\(x=0\) hasta\(x=4\).
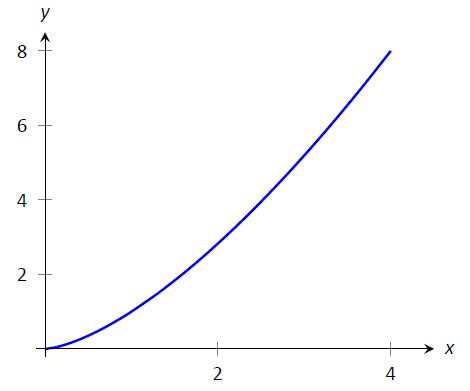
Figura\(\PageIndex{3}\): Un gráfico\(f(x) = x^{3/2}\) del Ejemplo\(\PageIndex{1}\)
Solución
Empezamos por encontrar\(f'(x)= \frac32x^{1/2}\). Usando la fórmula, encontramos la longitud del arco\(L\) como
\[\begin{align} L &= \int_0^4 \sqrt{1+\left(\frac32x^{1/2}\right)^2}\ dx \\ &= \int_0^4 \sqrt{1+\frac94x} \ dx \\ &= \int_0^4 \left(1+\frac94x\right)^{1/2}\ dx \\ &= \frac23\frac49\left(1+\frac94x\right)^{3/2}\Big|_0^4 \\ &=\frac{8}{27}\left(10^{3/2}-1\right) \approx 9.07 \text{units}.\end{align}\]
Ejemplo\(\PageIndex{2}\): Finding arc length
Encuentra la longitud del arco de\(f(x) =\frac18x^2-\ln x\) desde\(x=1\) hasta\(x=2\).
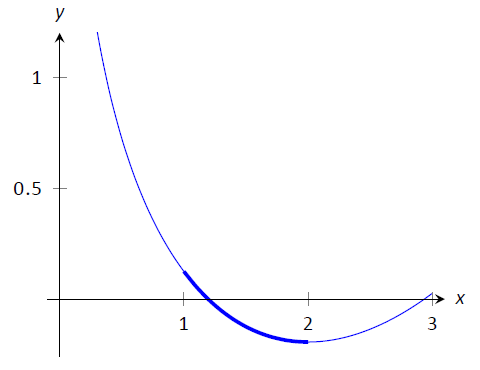
Figura\(\PageIndex{4}\): Una gráfica\(f(x) =\frac18x^2-\ln x\) del Ejemplo\(\PageIndex{2}\).
Solución
Esta función se eligió específicamente porque la integral resultante puede evaluarse exactamente. Empezamos por encontrar\(f'(x) = x/4-1/x\). La longitud del arco es
\[\begin{align} L&= \int_1^2 \sqrt{1+ \left(\frac x4-\frac1x\right)^2}\ dx \\ &= \int_1^2 \sqrt{1 + \frac{x^2}{16} -\frac12 + \frac1{x^2} } \ dx \\ &= \int_1^2 \sqrt{\frac{x^2}{16} +\frac12 + \frac1{x^2} } \ dx \\ &= \int_1^2 \sqrt{ \left(\frac x4 + \frac1x\right)^2}\ dx &= \int_1^2 \left(\frac x4 + \frac1x\right) \ dx \\ &= \left(\frac{x^2}8 + \ln x\right)\Bigg|_1^2\\ &= \frac38+\ln 2 \approx 1.07 \ \text{units}.\end{align}\]
\(f\)Se da una gráfica de en la Figura\(\PageIndex{4}\); la porción de la curva medida en este problema está en negrita.
Los ejemplos anteriores encontraron la longitud del arco exactamente a través de una cuidadosa elección de las funciones. En general, las respuestas exactas son mucho más difíciles de conseguir y son necesarias aproximaciones numéricas.
Ejemplo\(\PageIndex{3}\): Approximating arc length numerically
Encuentra la longitud de la curva sinusoidal de\(x=0\) a\(x=\pi\).
Solución
Esto es algo así como una curiosidad matemática; en el Ejemplo 5.4.3 encontramos que el área bajo una “joroba” de la curva sinusoidal es de 2 unidades cuadradas; ahora estamos midiendo su longitud de arco.
La configuración es sencilla:\(f(x) = \sin x\) y\(f'(x) = \cos x\). Así
\[L = \int_0^\pi \sqrt{1+\cos^2x}\ dx.\]
Esta integral no puede ser evaluada en términos de funciones elementales por lo que la aproximaremos con el Método de Simpson con\(n=4\).
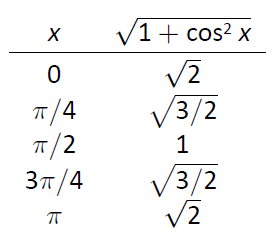
Figura\(\PageIndex{5}\): Una tabla de valores de\(y=\sqrt{1+\cos^2x}\) para evaluar una integral definida en Ejemplo\(\PageIndex{3}\).
\[\begin{array}{cc}x & \sqrt{1+\cos^2x} \\ \hline 0 & \sqrt{2}\\ \pi/4 & \sqrt{3/2} \\ \pi/2 & 1 \\ 3 \pi/4 & \sqrt{3/2} \\ \pi & \sqrt{2} \\\end{array}\]
Figura\ ref {fig:arc3} da\(\sqrt{1+\cos^2x}\) evaluado en 5 puntos uniformemente espaciados en\([0,\pi]\). La Regla de Simpson establece entonces que
\[\begin{align} \int_0^\pi \sqrt{1+\cos^2x}\ dx &\approx \frac{\pi-0}{4\cdot 3}\left(\sqrt{2}+4\sqrt{3/2}+2(1)+4\sqrt{3/2}+\sqrt{2}\right) \\ &=3.82918.\end{align}\]
Usar una computadora con\(n=100\) la aproximación es\(L\approx 3.8202\); nuestra aproximación con\(n=4\) es bastante buena.
Superficie de Sólidos de Revolución
Ya hemos visto cómo una curva\(y=f(x)\) on\([a,b]\) puede ser girada alrededor de un eje para formar un sólido. En lugar de computar su volumen, ahora consideramos su superficie.
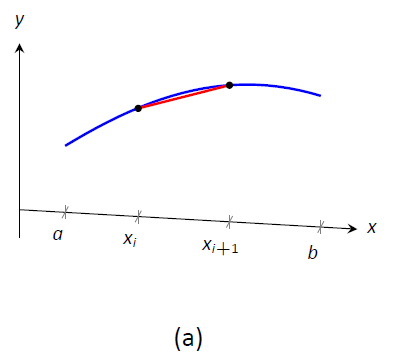
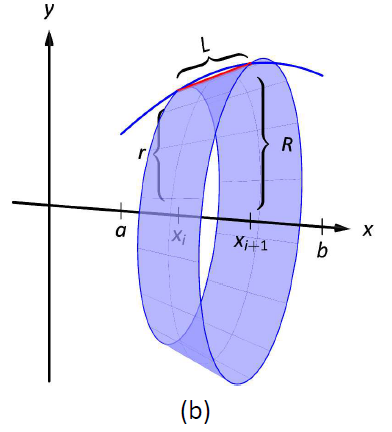
Figura\(\PageIndex{6}\): Establecer la fórmula para el área de superficie.
Comenzamos como tenemos en las secciones anteriores: particionamos el intervalo\([a,b]\) con\(n\) subintervalos, donde está el\(i\,^{\text{th}}\) subintervalo\([x_i,x_{i+1}]\). En cada subintervalo, podemos aproximar la curva\(y=f(x)\) con una línea recta que conecta\(f(x_i)\) y\(f(x_{i+1})\) como se muestra en la Figura\(\PageIndex{5a}\). Al girar este segmento de línea alrededor del\(x\) eje -eje se crea parte de un cono (llamado troncocono) como se muestra en la Figura\(\PageIndex{5b}\). El área de superficie de un tronco de cono es
\[2\pi\cdot\text{ length }\cdot\text{average of the two radii \(R\) and \(r\)}.\]
La longitud viene dada por\(L\); utilizamos el material que acaba de cubrir la longitud del arco para afirmar que
\[L\approx \sqrt{1+f'(c_i)}dx_i\]
para algunos\(c_i\) en el\(i\,^\text{th}\) subintervalo. Los radios son solo la función evaluada en los puntos finales del intervalo. Es decir,
\[R = f(x_{i+1})\quad \text{and}\quad r = f(x_i).\]
Así, el área superficial de esta muestra del tronco del cono es aproximadamente
\[2\pi\frac{f(x_i)+f(x_{i+1})}2\sqrt{1+f'(c_i)^2}dx_i.\]
Dado que\(f\) es una función continua, el Teorema del Valor Intermedio establece que hay algunos\(d_i\) en\([x_i,x_{i+1}]\) tal que\(f(d_i) = \frac{f(x_i)+f(x_{i+1})}2\); podemos usar esto para reescribir la ecuación anterior como
\[2\pi f(d_i)\sqrt{1+f'(c_i)^2}dx_i.\]
Sumando todos los subintervalos obtenemos que la superficie total sea aproximadamente
\[\text{Surface Area}\approx \sum_{i=1}^n 2\pi f(d_i)\sqrt{1+f'(c_i)^2}dx_i,\]
que es una suma de Riemann. Tomar el límite a medida que las longitudes del subintervalo van a cero nos da la superficie exacta, dada en la siguiente Idea Clave.
Idea Clave 28: Superficie de un Sólido de Revolución
Dejar\(f\) ser diferenciable en un intervalo abierto que contiene\([a,b]\) donde también\(f'\) es continuo encendido\([a,b]\).
- El área superficial del sólido formado al girar la gráfica de\(y=f(x)\), donde\(f(x)\geq0\), alrededor del\(x\) eje es
$$\ text {Superficie} = 2\ pi\ int_a^b f (x)\ sqrt {1+f' (x) ^2}\ dx.\]
- El área superficial del sólido formado al girar la gráfica de\(y=f(x)\) alrededor del\(y\) eje -, donde\(a,b\geq0\), es
$$\ text {Superficie} = 2\ pi\ int_a^b x\ sqrt {1+f' (x) ^2}\ dx.\]
Al girar\(y=f(x)\) alrededor del\(y\) eje, los radios del tronco resultante son\(x_i\) y\(x_{i+1}\); su valor promedio es simplemente el punto medio del intervalo. En el límite, este punto medio es justo\(x\). Esto da la segunda parte de Key Idea 28.
Ejemplo\(\PageIndex{4}\): Finding surface area of a solid of revolution
Encuentra el área de superficie del sólido formado al girar\(y=\sin x\)\([0,\pi]\) alrededor del\(x\) eje -como se muestra en la Figura\(\PageIndex{6}\).
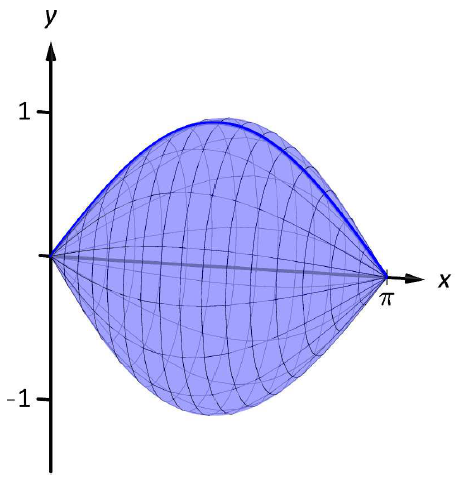
Figura\(\PageIndex{7}\):\(y=\sin x\) Girando\([0,\pi]\) alrededor del\(x\) eje.
Solución
La configuración es relativamente sencilla. Usando Key Idea\ ref {idea:surface_area}, tenemos el área de superficie\(SA\) es:
\[\begin{align}SA &= 2\pi\int_0^\pi \sin x\sqrt{1+\cos^2x}\ dx \\ &= -2\pi\frac12\left.\left(\sinh^{-1}(\cos x)+\cos x\sqrt{1+\cos^2x}\right)\right|_0^\pi \\ &= 2\pi\left(\sqrt{2}+\sinh^{-1} 1\right) \\ &\approx 14.42\ \text{units}^2.\end{align}\]
El paso de integración anterior es no trivial, utilizando un método de integración llamado Sustitución Trigonométrica.
Es interesante ver que el área superficial de un sólido, cuya forma está definida por una función trigonométrica, involucra tanto una raíz cuadrada como una función trigonométrica hiperbólica inversa.
Ejemplo\(\PageIndex{5}\): Finding surface area of a solid of revolution
Encuentra el área de superficie del sólido formado girando la curva\(y=x^2\) en\([0,1]\) aproximadamente:
- el\(x\) eje
- el\(y\) eje -.
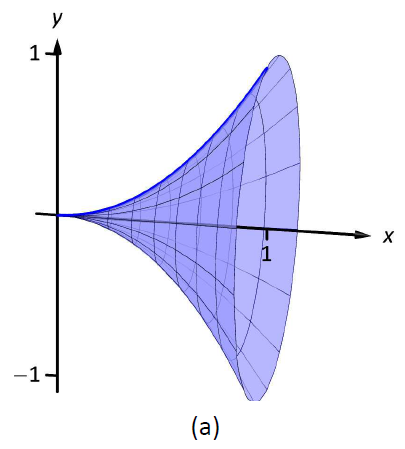
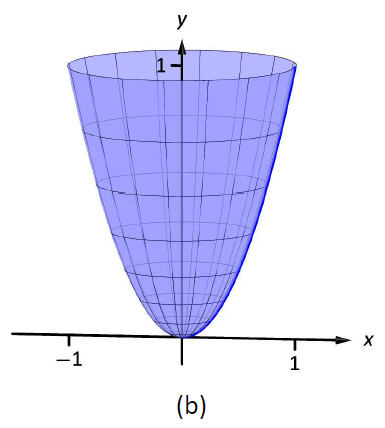
Figura\(\PageIndex{8}\): Los sólidos utilizados en el Ejemplo\(\PageIndex{6}\).
Solución
- La integral es sencilla de configurar:
\[SA = 2\pi\int_0^1 x^2\sqrt{1+(2x)^2} dx.\]
Al igual que la integral en Ejemplo\ ref {ex_sa1}, esto requiere Sustitución Trigonométrica.
\[\begin{align} &= \left.\frac{\pi}{32}\left(2(8x^3+x)\sqrt{1+4x^2}-\sinh^{-1}(2x)\right)\right|_0^1\\ &=\frac{\pi}{32}\left(18\sqrt{5}-\sinh^{-1}2\right)\\ &\approx 3.81\ \text{units}^2. \end{align}\]
El sólido formado al girar\(y=x^2\) alrededor del\(x\) eje se grafica en la Figura\(\PageIndex{7a}\).
- Como estamos girando alrededor del\(y\) eje -eje, el “radio” del sólido no lo es\(f(x)\) sino más bien\(x\). Así, la integral para calcular el área superficial es:
\[SA = 2\pi\int_0^1x\sqrt{1+(2x)^2} dx.\]
Esta integral se puede resolver mediante sustitución. Establecer\(u=1+4x^2\); los nuevos límites son\(u=1\) para\(u=5\). Entonces tenemos
\[\begin{align} &= \frac{\pi}{4}\int_1^5 \sqrt{u} du \\ &= \frac{\pi}{4}\frac{2}{3} u^{3/2}\big|_1^5 \\ &= \frac{\pi}{6}\left ( 5\sqrt{5}-1\right ) \\ &\approx 5.33 \text{ units}^2. \end{align}\]
El sólido formado al girar\(y=x^2\) alrededor del\(y\) eje se grafica en la Figura\(\PageIndex{7b}\).
Nuestro último ejemplo es una famosa “paradoja” matemática.
Ejemplo\(\PageIndex{6}\): The surface area and volume of Gabriel's Horn
Considere el sólido formado al girar\(y=1/x\) alrededor del\(x\) eje -en\([1,\infty)\). Encuentra el volumen y la superficie de este sólido. (Esta forma, como se grafica en Figura\(\PageIndex{9}\), es conocida como “Cuerno de Gabriel” ya que parece un cuerno muy largo que solo una persona sobrenatural, como un ángel, podría tocar.)
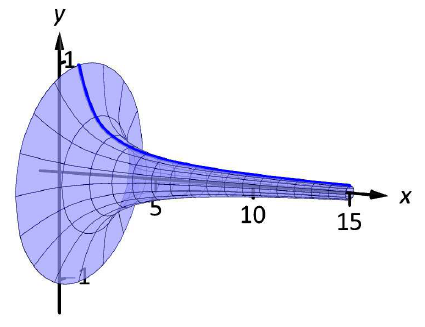
Figura\(\PageIndex{9}\): Gráfica del Cuerno de Gabriel.
Solución
Para calcular el volumen es natural usar el Método de Disco. Contamos con:
\[\begin{align}V &= \pi\int_1^\infty \frac{1}{x^2}\ dx \\ &= \lim_{b\to\infty}\pi\int_1^b\frac{1}{x^2}\ dx \\ &= \lim_{b\to\infty} \left.\pi\left(\frac{-1}{x}\right)\right|_1^b \\ &= \lim_{b\to\infty} \pi\left(1-\frac1b\right) \\ &= \pi \ \text{units}^3.\end{align}\]
Cuerno de Gabriel tiene un volumen finito de unidades\(\pi\) cúbicas. Como ya hemos visto que las regiones con longitud infinita pueden tener un área finita, esto no es demasiado difícil de aceptar.
Consideramos ahora su superficie. La integral es sencilla de configurar:
\[SA = 2\pi\int_1^\infty \frac{1}{x}\sqrt{1+1/x^4}\ dx.\]
Integrar esta expresión no es trivial. Podemos, sin embargo, compararlo con otras integrales impropias. Desde entonces\(1< \sqrt{1+1/x^4} \)\([1,\infty)\), podemos afirmar que
\[2\pi\int_1^\infty \frac{1}{x} dx <2\pi\int_1^\infty \frac{1}{x}\sqrt{1+1/x^4} dx .\]
Por Key Idea 21, la integral impropia de la izquierda diverge. Dado que la integral de la derecha es más grande, concluimos que también diverge, lo que significa que el Cuerno de Gabriel tiene una superficie infinita.
De ahí la “paradoja”: podemos llenar el Cuerno de Gabriel con una cantidad finita de pintura, pero como tiene una superficie infinita, nunca podremos pintarlo.
De alguna manera esta paradoja llama la atención cuando la pensamos en términos de volumen y área. Sin embargo, antes hemos visto una paradoja similar, como se mencionó anteriormente. Sabemos que el área bajo la curva\(y=1/x^2\)\([1,\infty)\) es finita, sin embargo, la forma tiene un perímetro infinito. Cosas extrañas pueden ocurrir cuando tratamos con lo infinito.
Una ecuación estándar de la física es “Trabajo =\(\times\) distancia de fuerza”, cuando la fuerza aplicada es constante. En la siguiente sección aprendemos a calcular el trabajo cuando la fuerza aplicada es variable.


