9.4: Introducción a las coordenadas polares
- Page ID
- 111959
Generalmente se nos introduce la idea de graficar curvas relacionando -valores con\(x\) -valores a\(y\) través de una función\(f\). Es decir\(y=f(x)\), establecemos y trazamos muchos pares de puntos\((x,y)\) para obtener una buena idea de cómo se ve la curva. Este método es útil pero tiene limitaciones, no menos importante de las cuales es que las curvas que “fallan en la prueba de línea vertical” no se pueden graficar sin usar múltiples funciones.
Las dos secciones anteriores introdujeron y estudiaron una nueva forma de trazar puntos en el\(x,y\) plano. Usando ecuaciones paramétricas,\(x\) y\(y\) los valores se computan de forma independiente y luego se trazan juntos. Este método nos permite graficar un extraordinario rango de curvas. Esta sección introduce otra forma más de trazar puntos en el plano: usando coordenadas polares.
Coordenadas polares
Empezar con un punto\(O\) en el plano llamado polo (siempre identificaremos este punto con el origen). Desde el polo, dibuja un rayo, llamado rayo inicial (siempre dibujaremos este rayo horizontalmente, identificándolo con el\(x\) eje positivo). Un punto\(P\) en el plano está determinado por la distancia\(r\) que\(P\) es desde\(O\), y el ángulo\(\theta\) formado entre el rayo inicial y el segmento\(\overline{OP}\) (medido en sentido antihorario). Registramos la distancia y el ángulo como un par ordenado\((r,\theta)\). Para evitar confusiones con coordenadas rectangulares, denotaremos coordenadas polares con la letra\(P\), como en\(P(r,\theta)\). Esto se ilustra en la Figura\(\PageIndex{1}\).
La práctica hará más claro este proceso.
Ejemplo\(\PageIndex{1}\): Plotting Polar Coordinates
Trace las siguientes coordenadas polares:
\[A = P(1,\pi/4)\quad B=P(1.5,\pi)\quad C = P(2,-\pi/3)\quad D = P(-1,\pi/4)\]
Solución
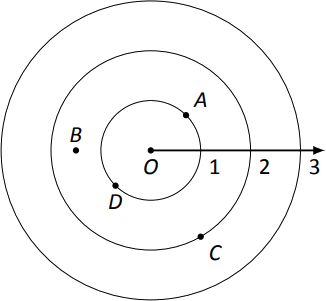
Para ayudar en el dibujo, se proporciona una cuadrícula polar en la parte inferior de esta página. Para colocar el punto\(A\), salga 1 unidad a lo largo del rayo inicial (poniéndote en el círculo interno que se muestra en la cuadrícula), luego gira\(\pi/4\) radianes en sentido antihorario (o\(45^\circ\)). Como alternativa, uno puede considerar primero la rotación: piensa en el rayo desde\(O\) que forma un ángulo de\(\pi/4\) con el rayo inicial, luego mueve hacia fuera 1 unidad a lo largo de este rayo (nuevamente colocándote en el círculo interno de la cuadrícula).
Para trazar\(B\), salga\(1.5\) unidades a lo largo del rayo inicial y rote\(\pi\) radianes (\(180^\circ\)).
Para trazar\(C\), salga 2 unidades a lo largo del rayo inicial y luego gire\(\pi/3\) radianes en sentido horario, ya que el ángulo dado es negativo.
Para trazar\(D\), muévase a lo largo de las unidades\(-1\) "" del rayo inicial — en otras palabras, “retroceda” 1 unidad, luego gire en sentido antihorario por\(\pi/4\). Los resultados se dan en la Figura\(\PageIndex{2}\).
Considerar los dos puntos siguientes:\(A = P(1,\pi)\) y\(B = P(-1,0)\). Para ubicar\(A\), salga 1 unidad en el rayo inicial luego gire\(\pi\) radianes; para ubicar\(B\), salga\(-1\) unidades en el rayo inicial y no rote. Uno debería ver eso\(A\) y\(B\) están ubicados en el mismo punto del avión. También podemos considerar\(C=P(1,3\pi)\), o\(D = P(1,-\pi)\); los cuatro de estos puntos comparten la misma ubicación.
Esta habilidad para identificar un punto en el plano con múltiples coordenadas polares es tanto una “bendición” como una “maldición”. Veremos que es beneficioso ya que podemos trazar hermosas funciones que se cruzan (al igual que vimos con funciones paramétricas). La parte desafortunada de esto es que puede ser difícil determinar cuándo sucede esto. Exploraremos esto más adelante en esta sección.
Conversión de Polar a Rectangular
Es útil reconocer tanto las coordenadas rectangulares (o, cartesianas) de un punto en el plano como sus coordenadas polares. La figura\(\PageIndex{3}\) muestra un punto\(P\) en el plano con coordenadas rectangulares\((x,y)\) y coordenadas polares\(P(r,\theta)\). Utilizando la trigonometría, podemos hacer las identidades dadas en la siguiente Idea Clave.
KEY IDEA 40 Conversión entre coordenadas rectangulares y polares
Dado el punto polar\(P(r,\theta)\), las coordenadas rectangulares están determinadas por
\[x=r\cos \theta\qquad y=r\sin \theta.\]
Dadas las coordenadas rectangulares\((x,y)\), las coordenadas polares están determinadas por
\[ r^2=x^2+y^2\qquad \tan \theta = \frac yx.\]
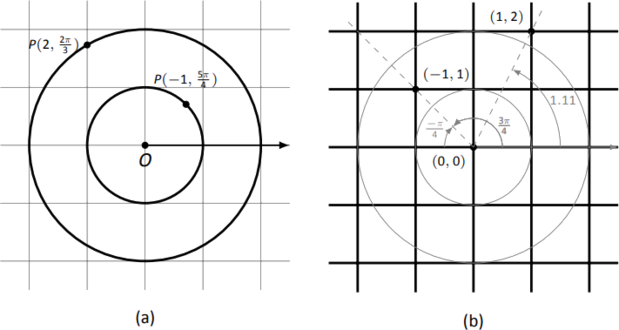
Ejemplo\(\PageIndex{2}\): Converting Between Polar and Rectangular Coordinates
- Convertir las coordenadas polares\(P(2,2\pi/3)\) y\(P(-1,5\pi/4)\) en coordenadas rectangulares.
- Convertir las coordenadas rectangulares\((1,2)\) y\((-1,1)\) en coordenadas polares.
- (a) Empezamos con\(P(2,2\pi/3)\). Usando Key Idea 40, tenemos\[x= 2\cos (2\pi/3) = -1\qquad y = 2\sin (2\pi/3) = \sqrt{3}.\] Así que las coordenadas rectangulares son\((-1,\sqrt{3}) \approx (-1,1.732)\).
(b) El punto polar\(P(-1,5\pi/4)\) se convierte a rectangular con:\[x=-1\cos (5\pi/4) = \sqrt{2}/2\qquad y= -1\sin (5\pi/4) = \sqrt{2}/2.\]
Entonces las coordenadas rectangulares son\((\sqrt{2}/2,\sqrt{2}/2) \approx (0.707,0.707)\).
Estos puntos se trazan en la Figura\(\PageIndex{4}\) (a). El sistema de coordenadas rectangulares se dibuja ligeramente bajo el sistema de coordenadas polares para que se pueda ver la relación entre los dos.
- (a) Para convertir el punto\((1,2)\) rectangular en coordenadas polares, utilizamos la Idea Clave para formar las dos ecuaciones siguientes:
\[1^2+2^2 = r^2 \qquad \tan \theta = \frac{2}{1}.\] La primera ecuación nos dice eso\(r=\sqrt{5}\). Usando la función tangente inversa, encontramos\[\tan \theta = 2 \quad \Rightarrow \quad \theta = \tan^{-1} 2 \approx 1.11\approx 63.43^\circ.\] Así coordenadas polares de\((1,2)\) son\(P(\sqrt{5},1.11)\).
(b) Para convertir\((-1,1)\) a coordenadas polares, formamos las ecuaciones\[(-1)^2+1^2=r^2 \qquad \tan \theta = \frac{1}{-1}.\]
Así\(r=\sqrt{2}\). Hay que tener cuidado en la computación\(\theta\): usando la función tangente inversa, tenemos\[\tan\theta = -1 \quad \Rightarrow \quad \theta = \tan^{-1}(-1) = -\pi/4 = -45^\circ.\]
Este no es el ángulo que deseamos. El rango de\(\tan^{-1}x\) es\((-\pi/2,\pi/2)\); es decir, devuelve ángulos que se encuentran en los\(4^\text{th}\) cuadrantes\(1^\text{st}\) y. Para encontrar ubicaciones en los\(3^\text{rd}\) cuadrantes\(2^\text{nd}\) y, agregue\(\pi\) al resultado de\(\tan^{-1}x\). Así\(\pi+(-\pi/4)\) pone el ángulo en\(3\pi/4\). Así es el punto polar\(P(\sqrt{2},3\pi/4)\).
Un método alternativo es usar el ángulo\(\theta\) dado por el arcotangente, pero cambiar el signo de\(r\). Así también podríamos referirnos\((-1,1)\) como\\\(P(-\sqrt{2},-\pi/4)\).
Estos puntos se trazan en la Figura\(\PageIndex{4}\) (b). El sistema polar se dibuja ligeramente bajo la rejilla rectangular con rayos para demostrar los ángulos utilizados.
Funciones polares y gráficas polares
Definir un nuevo sistema de coordenadas nos permite crear un nuevo tipo de función, una función polar. Las coordenadas rectangulares se prestaron bien a crear funciones que relacionaban\(x\) y\(y\), como las coordenadas\(y=x^2.\) polares nos permiten crear funciones que se relacionan\(r\) y\(\theta\). Normalmente estas funciones se ven así\(r=f(\theta)\), aunque podemos crear funciones de la forma\(\theta = f(r)\). Los siguientes ejemplos nos introducen en este concepto.
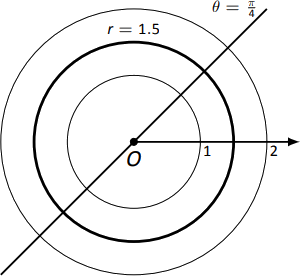
Ejemplo\(\PageIndex{3}\): Introduction to Graphing Polar Functions
Describir las gráficas de las siguientes funciones polares.
- \(r = 1.5\)
- \(\theta = \pi/4 \)
Solución
- La ecuación\(r=1.5\) describe todos los puntos que están a 1.5 unidades del polo; como no se especifica el ángulo, ninguno\(\theta\) es permisible. Todos los puntos 1.5 unidades del polo describen un círculo de radio 1.5.
Podemos considerar el equivalente rectangular de esta ecuación; usando\(r^2=x^2+y^2\), vemos eso\(1.5^2=x^2+y^2\), que reconocemos como la ecuación de un círculo centrado en\((0,0)\) con radio 1.5. Esto se esboza en la Figura\(\PageIndex{5}\). - La ecuación\(\theta = \pi/4\) describe todos los puntos de tal manera que la línea a través de ellos y el polo forman un ángulo de\(\pi/4\) con el rayo inicial. Como no\(r\) se especifica el radio, puede ser cualquier valor (incluso negativo). Así\(\theta = \pi/4\) describe la línea a través del polo que forma un ángulo de\(\pi/4 = 45^\circ\) con el rayo inicial.
Podemos volver a considerar el equivalente rectangular de esta ecuación. Combinar\(\tan \theta =y/x\) y\(\theta =\pi/4\):\[\tan \pi/4 = y/x \quad \Rightarrow x\tan \pi/4 = y \quad \Rightarrow y = x.\] Esta gráfica también se grafica en la Figura\(\PageIndex{5}\).
Las ecuaciones rectangulares básicas de la forma\(x=h\) y\(y=k\) crean líneas verticales y horizontales, respectivamente; las ecuaciones polares básicas\(r= h\) y\(\theta =\alpha\) crean círculos y líneas a través del polo, respectivamente. Con esto como fundamento, podemos crear funciones polares más complicadas de la forma\(r=f(\theta)\). La entrada es un ángulo; la salida es una longitud, qué tan lejos en la dirección del ángulo para salir.
Esbozamos estas funciones de manera muy parecida a las funciones rectangulares y paramétricas: trazamos muchos puntos y “conectamos los puntos” con curvas. Esto lo demostramos en el siguiente ejemplo.
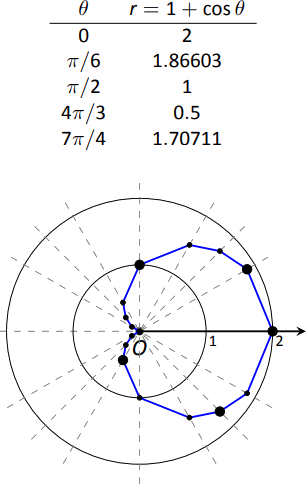
Ejemplo\(\PageIndex{4}\): Sketching Polar Functions
Dibuje la\(r=1+\cos \theta\) función polar\([0,2\pi]\) trazando puntos.
Solución
Una pregunta común al bosquejar curvas trazando puntos es “¿Qué puntos debo trazar?” Con ecuaciones rectangulares, a menudo elegimos valores “fáciles” — enteros, luego agregamos más si es necesario. Al trazar ecuaciones polares, comience con los ángulos “comunes” — múltiplos de\(\pi/6\) y\(\pi/4\). La figura\(\PageIndex{6}\) da una tabla de solo unos pocos valores de\(\theta\) in\([0,\pi]\).
Considera el punto\(P(0,2)\) determinado por la primera línea de la tabla. El ángulo es de 0 radianes —no giramos desde el rayo inicial— luego salimos 2 unidades del polo. Cuando\(\theta=\pi/6\),\(r = 1.866\) (en realidad, lo es\(1+\sqrt{3}/2\)); así rote por\(\pi/6\) radianes y salga 1.866 unidades.
La gráfica mostrada utiliza más puntos, conectados con líneas rectas. (Los puntos en la gráfica que corresponden a los puntos de la tabla se significan con puntos más grandes). Tal boceto probablemente sea lo suficientemente bueno como para darle una idea de cómo se ve la gráfica.
Nota Tecnológica
Trazar funciones de esta manera puede ser tedioso, tal como lo fue con las funciones rectangulares. Para obtener gráficas muy precisas, la tecnología es de gran ayuda. La mayoría de las calculadoras gráficas pueden trazar funciones polares; en el menú, establece el modo de trazado en algo así como\(\texttt{polar}\) o\(\texttt{POL}\), dependiendo de la calculadora de uno. Al igual que con las funciones paramétricas de trazado, la “ventana” de visualización ya no determina los\(x\) -valores que se trazan, por lo que es necesario proporcionar información adicional. A menudo con la configuración de “ventana” son los ajustes para los\(\theta\) valores inicial y final (a menudo llamados\(\theta_{\text{min}}\) y\(\theta_{\text{max}}\)) así como el\(\theta_{\text{step}}\) — es decir, qué tan separados están los\(\theta\) valores espaciados. Cuanto menor sea el\(\theta_{\text{step}}\) valor, más precisa es la gráfica (lo que también aumenta el tiempo de trazado). Usando la tecnología, graficamos la función polar\(r=1+\cos \theta\) del Ejemplo 9.4.4 en la Figura\(\PageIndex{7}\).
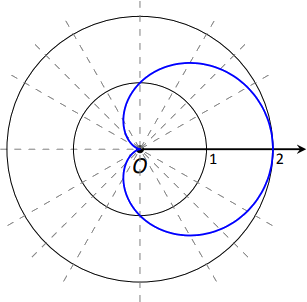
Ejemplo\(\PageIndex{5}\): Sketching Polar Functions
Dibuje la\(r=\cos (2\theta)\) función polar\([0,2\pi]\) trazando puntos.
Solución
Comenzamos haciendo una tabla de\(\cos (2\theta)\) evaluados en ángulos comunes\(\theta\), como se muestra en la Figura\(\PageIndex{8}\). Estos puntos se trazan luego en la Figura\(\PageIndex{9}\) (a). Esta gráfica en particular “se mueve” bastante y uno puede olvidar fácilmente qué puntos deben estar conectados entre sí. Para ayudarnos con esto, numeramos cada punto en la tabla y en la gráfica.
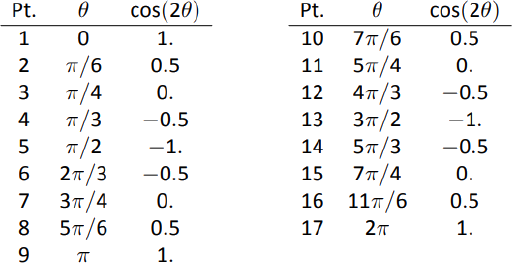
Usando más puntos (y la ayuda de la tecnología) se puede hacer una gráfica más suave como se muestra en la Figura\(\PageIndex{9}\) (b). Esta trama es un ejemplo de una curva de rosa.
A veces es deseable referirse a una gráfica a través de una ecuación polar, y otras veces por una ecuación rectangular. Por lo tanto es necesario poder convertir entre funciones polares y rectangulares, lo que practicamos en el siguiente ejemplo. Haremos un uso frecuente de las identidades que se encuentran en Key Idea 40.
Ejemplo\(\PageIndex{6}\): Converting between rectangular and polar equations.
Convierte de rectangular a polar.
- \(y=x^2\)
- \(xy = 1\)
Convierte de polar a rectangular.
- \( r=\frac{2}{\sin \theta-\cos\theta}\)
- \(r=2\cos \theta\)
Solución
- Reemplazar\(y\) con\(r\sin\theta\) y reemplazar\(x\) con\(r\cos\theta\), dando:
\[\begin{align*}y &=x^2\\r\sin\theta &= r^2\cos^2\theta\\\frac{\sin\theta}{\cos^2\theta} &= r\end{align*}\]
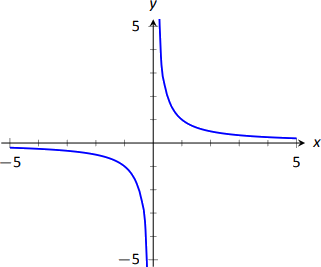
Lo hemos encontrado\(r=\sin\theta/\cos^2\theta = \tan\theta\sec\theta\). El dominio de esta función polar es\((-\pi/2,\pi/2)\); trazar algunos puntos para ver cómo la parábola familiar es trazada por la ecuación polar. - Nuevamente reemplazamos\(x\) y\(y\) usamos las identidades estándar y trabajamos para resolver para\(r\):\[\begin{align*}xy &= 1 \\r\cos\theta\cdot r\sin\theta & = 1\\r^2 & = \frac{1}{\cos\theta\sin\theta}\\r & = \frac{1}{\sqrt{\cos\theta\sin\theta}}\\\end{align*}\]
Esta función es válida solo cuando el producto de\(\cos\theta\sin\theta\) es positivo. Esto ocurre en el primer y tercer cuadrantes, es decir, el dominio de esta función polar es\((0,\pi/2) \cup (\pi,3\pi/2)\).
Podemos reescribir la ecuación rectangular original\(xy=1\) como\(y=1/x\). Esto se grafica en la Figura\(\PageIndex{10}\); fíjese como solo existe en el primer y tercer cuadrantes.
- No hay una forma establecida de convertir de polar a rectangular; en general, buscamos formar los productos\(r\cos \theta\) y\(r\sin\theta\), y luego reemplazarlos con\(x\) y\(y\), respectivamente. Comenzamos en este problema multiplicando ambos lados por\(\sin\theta-\cos\theta\):
\[\begin{align*}r &= \frac{2}{\sin\theta-\cos\theta} \\r(\sin\theta-\cos\theta) &= 2\\r\sin\theta-r\cos\theta &= 2. \qquad \text{Now replace with \(y\) and \(x\):}\\y-x &= 2\\y &= x+2.\end{align*}\]
La ecuación polar original,\(r=2/(\sin\theta-\cos\theta)\) no revela fácilmente que su gráfica es simplemente una línea. No obstante, nuestra conversión demuestra que lo es. La próxima galería de curvas polares da las ecuaciones generales de líneas en forma polar. - Al multiplicar ambos lados por\(r\), obtenemos tanto un\(r^2\) término como un\(r\cos\theta\) término, que reemplazamos por\(x^2+y^2\) y\(x\), respectivamente.
\[\begin{align*}r &=2\cos\theta \\r^2 &= 2r\cos\theta \\x^2+y^2 &= 2x. \end{align*}\]Esto lo reconocemos como un círculo; al completar el cuadrado podemos encontrar su radio y centro.
\[\begin{align}x^2-2x+y^2 &= 0 \\(x-1)^2 + y^2 &=1.\end{align}\]
El círculo está centrado en\((1,0)\) y tiene radio 1. La próxima galería de curvas polares da las ecuaciones de algunos círculos en forma polar; los círculos con centros arbitrarios tienen una ecuación polar complicada que no consideramos aquí.
Algunas curvas tienen ecuaciones polares muy simples pero rectangulares bastante complicadas. Por ejemplo, la ecuación\(r=1+\cos\theta\) describe un cardiod (una forma importante la sensibilidad de los micrófonos, entre otras cosas; uno se grafica en la galería en la sección Lima\ c con). Su forma rectangular no es tan simple; es la ecuación implícita
\[x^4+y^4+2x^2y^2-2xy^2-2x^3-y^2=0.\]
La conversión no es “dura”, sino que da varios pasos, y se deja como un problema en la sección Ejercicio.
Galería de Curvas polares
Hay una serie de curvas polares básicas y “clásicas”, famosas por su belleza y/o aplicabilidad a las ciencias. Esta sección termina con una pequeña galería de algunas de estas gráficas. Animamos al lector a comprender cómo se forman estas gráficas, e investigar con tecnología otros tipos de funciones polares.
Anteriormente discutimos cómo cada punto en el plano no tiene una representación única en forma polar. Esto puede ser algo “bueno”, ya que permite las hermosas e interesantes curvas vistas en la galería anterior. Sin embargo, también puede ser algo “malo”, ya que puede ser difícil determinar dónde se cruzan dos curvas.
Ejemplo\(\PageIndex{7}\): Finding points of intersection with polar curves
Determinar dónde se cruzan las gráficas de las ecuaciones polares\(r=1+3\cos\theta\) y se\(r=\cos \theta\) cruzan.
Solución
Como la tecnología generalmente está fácilmente disponible, generalmente es una buena idea comenzar con una gráfica. Hemos graficado las dos funciones en la Figura\(\PageIndex{11}\) (a); para discernir mejor los puntos de intersección, la parte (b) de la figura se acerca al origen.
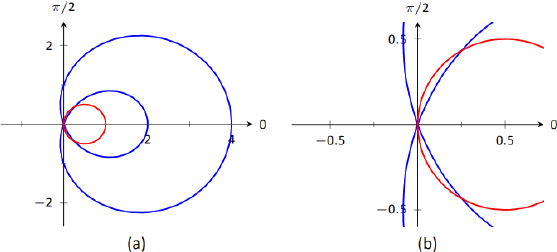
Comenzamos estableciendo las dos funciones iguales entre sí y resolviendo para\(\theta\):
\ [\ begin {align*}
1+3\ cos\ theta &=\ cos\ theta\\
2\ cos\ theta &= -1\\
\ cos\ theta&= -\ frac12\
\ theta &=\ frac {2\ pi} {3},\ frac {4\ pi} {3}.
\ end {alinear*}\]
(Hay, por supuesto, infinitas soluciones a la ecuación\(\cos\theta=-1/2\); como la lima\ c con se traza una vez\([0,2\pi]\), restringimos nuestras soluciones a este intervalo.)
Necesitamos analizar esta solución. Cuando\(\theta = 2\pi/3\) obtenemos el punto de intersección que se encuentra en el\(^\text{th}\) cuadrante 4. Cuando\(\theta = 4\pi/3\), obtenemos el punto de intersección que se encuentra en el\(^\text{nd}\) cuadrante 2. Sin embargo, hay más que decir sobre este segundo punto de intersección. El círculo definido por\(r=\cos\theta\) se traza una vez encendido\([0,\pi]\), lo que significa que este punto de intersección ocurre mientras se traza el círculo por segunda vez. Parece extraño pasar una vez por el punto y luego reconocerlo como un punto de intersección sólo al llegar allí una “segunda vez”. La primera vez que el círculo llega a este punto es cuando\(\theta = \pi/3\).
Es clave entender que estos dos puntos son los mismos:\((\cos \pi/3,\pi/3)\) y\((\cos 4\pi/3,4\pi/3)\).
Para resumir lo que hemos hecho hasta ahora, hemos encontrado dos puntos de intersección: cuándo\(\theta=2\pi/3\) y cuándo\(\theta=4\pi/3\). Al hacer referencia al círculo\(r=\cos \theta\), este último punto es mejor referenciado como cuándo\(\theta=\pi/3\).
Hay otro punto de intersección: el polo (o, el origen). No reconocimos este punto de intersección usando nuestro trabajo anterior ya que cada gráfica llega al poste a un\(\theta\) valor diferente.
Una gráfica cruza el polo cuando\(r=0\). Considerando el círculo\(r=\cos\theta\),\(r=0\) cuándo\(\theta = \pi/2\) (y múltiplos impares del mismo, ya que el círculo se traza repetidamente). La lima\ c con cruza el polo cuando\(1+3\cos\theta =0\); esto ocurre cuando\(\cos \theta = -1/3\), o para\(\theta = \cos^{-1}(-1/3)\). Este es un ángulo no estándar, aproximadamente\(\theta = 1.9106 = 10\(\PageIndex{12}\) ^\ circ\). La lima\ c con cruza el polo dos veces en\([0,2\pi]\); el otro ángulo en el que la lima\ c con está en el polo es la reflexión del primer ángulo a través del\(x\) eje. Es decir,\(\theta = 4.3726 = 250.53^\circ.\)
Si a lo único que se le preocupa son las\((x,y)\) coordenadas en las que se cruzan las gráficas, gran parte del trabajo anterior es extraño. Sabemos que se cruzan en\((0,0)\); puede que no nos importe en qué\(\theta\) valor. Así mismo, usando\(\theta =2\pi/3\) y nos\(\theta=4\pi/3\) puede dar las coordenadas rectangulares necesarias. Sin embargo, en la siguiente sección aplicamos conceptos de cálculo a las funciones polares. Al calcular el área de una región delimitada por curvas polares, se vuelve importante comprender los matices de los puntos de intersección.